Обработка эмпирических данных исследования (стр. 2 )

Наиболее часто применяются равные интервалы, но при неравномерном распределении частот группировочного признака для выделения качественно отличных типов явлений можно применять интервалы различной величины.

Таблицы. Их применяют в целях лучшей наглядности представляемой информации и удобства сравнения показателей.

Простые таблицы представляют собой перечень отдельных значений данных с количественной (или качественной) характеристикой каждого из них в отдельности. К простым таблицам относятся и таблицы, характеризующие динамику некоторых показателей (табл. 5.1).

Таблица 5.1

Показатели работы отдела социальной защиты
в первом квартале года

В групповых таблицах данные группируются по одному признаку. Например, опрос 38 семей показал, что на вопрос: «Сколько детей вы желаете иметь?», ответы распределились следующим образом: пять –
2 семьи, четверо – 4 семьи, трое – 5 семей, двое – 18 семей, одного –
6 семей, ни одного – 3 семьи. Эта информация может быть представлена в виде групповой таблицы (табл. 5.2).

Таблица 5.2

Распределение респондентов
по желаемому числу детей в семье

В комбинационных таблицах данные группируются по двум и более признакам (табл. 5.3).

Комбинационные таблицы позволяют более детально проанализировать исследуемое социальное явление. В частности, на основе информации, приводимой в табл. 5.3, можно сделать вывод, что отсутствие желания иметь детей в семье определяется, в первую очередь, не качеством жилищных условий опрошенных семей, а другими факторами. В то же время очевидна закономерность – улучшение жилищных условий семьи приводит к увеличению желаемого количества детей.

Таблица 5.3

Распределение респондентов
по желаемому числу детей в семье

При изложении информации в табличной форме следует обращать внимание на правильность оформления. Основные требования к табличной информации:

1)  таблица должна иметь нумерационный заголовок (номер таблицы – арабскими цифрами).

2)  тематический заголовок, при его наличии, должен отражать ее содержание, быть кратким и точным;

3)  тематический заголовок (название) следует помещать над таблицей;

4)  таблицу следует располагать непосредственно после текста, в котором она упоминается впервые, или на следующей странице;

5)  на все таблицы должны быть ссылки в тексте. При ссылке следует писать слово «таблица» с указанием ее номера;

6)  таблицу с большим количеством строк допускается переносить на другой лист (страницу);

Графическое отображение информации. Для повышения наглядности результатов количественного анализа данных их удобно представлять в графической форме в виде различных диаграмм, гистограмм, полигонов частот дискретных рядов и т. д. (рис. 5.1).

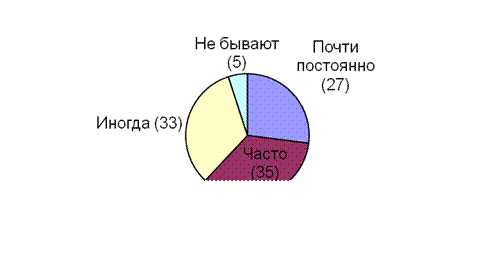
Рис. 1. Конфликты в семьях,

связанные с жилищными условиями, %

Одномерные распределения принято изображать в виде гистограмм. Гистограмма представляет собой графическое изображение интервального ряда. По горизонтальной оси графика откладываются границы интервалов, на которых при равных интервалах строят прямоугольники с высотой, пропорциональной частотам. На рис. 5.2 представлена гистограмма, построенная по данным табл. 5.2. Если интервалы различны по величине, высота прямоугольников уменьшается или увеличивается.

Полигоны распределения представляют собой графики, построенные по точкам значений частот или частостей, соответствующих серединам интервалов интервальных рядов или значениям дискретных рядов (рис. 5.3).

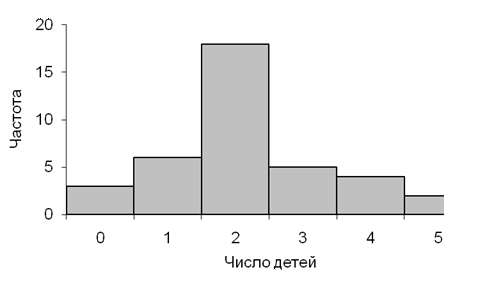
Рис. 5.2. Гистограмма распределения респондентов
по желаемому числу детей в семье

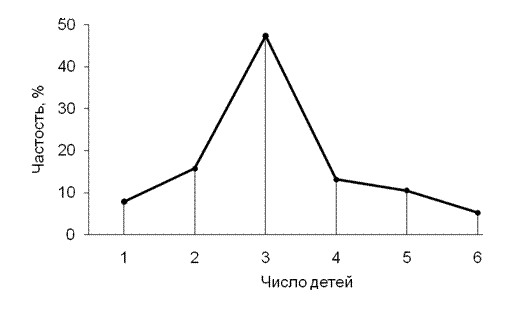
Рис. 5.3. Полигон распределения респондентов
по желаемому числу детей в семье

Для графического изображения вариационных рядов преимущественно используют кумулятивные кривые. При их построении, как и для полигонов распределения, по оси абсцисс откладываются середины интервалов интервальных рядов или значения дискретных рядов, а по оси ординат – накопленные суммы частот или частостей (рис. 5.4). 

С помощью кумуляты можно легко определять процент респондентов, находящихся ниже или выше заданной величины исследуемого признака. Например, по рис. 5.4 можно определить, что количество семей, считающих оптимальным количество детей от трех и более, составляет 29 % от общего числа опрошенных.

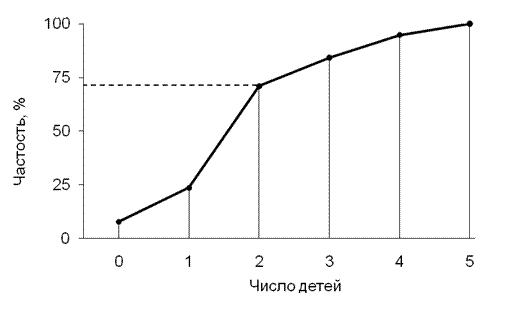
Рис. 5.4. Кумулята распределения респондентов
по желаемому числу детей в семье

Кривые распределения, построенные по эмпирическим данным, могут иметь разнообразную форму. Анализ формы кривых иногда позволяет оценить внутреннюю структуру исследуемых данных.

Вычисление статистических характеристик. Основными статистическими показателями, используемыми при обобщении полученных данных, являются среднее арифметическое, среднее квадратическое, дисперсия, коэффициент вариации, мода и медиана.

Наиболее часто применяют средние арифметические значения (средние величины). В зависимости от исходных данных средние арифметические значения могут рассчитываться различными способами.

Если известны значения признака у отдельных единиц совокупности, то среднее арифметическое значение можно вычислить в виде частного от деления суммы всех значений признака на число членов ряда:

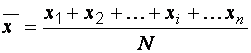  (5.1)

или

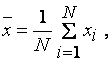   (5.2)

где  – среднее арифметическое;  – значения данных;  – количество членов ряда.

Проанализируем сведения о количестве членов семей, проживающих в городе и в сельской местности:

Каждый из рядов состоит из 16 членов. Среднее арифметическое значение количества членов семей, проживающих в городе и в сельской местности, рассчитанные по формулам (5.1) или (5.2), составляют 2,8 и 3,8 человек соответственно.

Если данные сгруппированы и представлены в виде вариационного ряда, необходимо рассчитывать средние взвешенные, которые вычисляются с учетом весов каждой варианты:

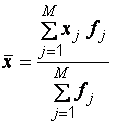,  (5.3)

где  – среднее арифметическое;  – значения вариант в -м интервале;  – вес -й варианты;  – количество интервалов.

Рассчитаем средний месячный доход на одного члена семьи по данным табл. 5.4. Обратите внимание, что величина интервалов различна, а середина каждого интервала вычисляется приближенно.

Таблица 5.4

Расчет среднего месячного дохода на одного члена семьи

Исходя из полученных итоговых результатов можно рассчитать, что средний месячный доход на одного члена семьи составляет 4353 рубля.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5