Лабораторная работа №5
”Организация рекурсивных вычислений”

 

Основные цели работы

Целью работы является получение навыков организации рекурсивных вычислений

Требования к разрабатываемой программе

В математической формулировке задачи должны быть приведены рекуррентные соотношения для первого и второго заданий.

Во втором задании при выводе результата вывести:

-     расчетное значение функции для итерационного и рекурсивного алгоритмов, а также стандартное значение функции

-     значение количества членов ряда, которое необходимо просуммировать для достижения указанной точности

-     сравнить время выполнения алгоритмов, используя стандартную функцию gettime модуля dos.

Варианты индивидуального задания

Вариант 1

1. Вычислить значение функции Х(n) при заданном значении n, используя рекурсию. Знаки перед корнями периодически повторяются группами по три: "-","+","-".

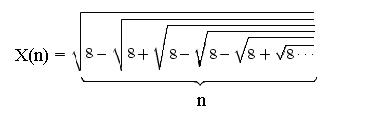
Заданы: значение х, точность e. Составить подпрограмму расчета функции F(x) с точностью e, используя рекурсивный и итерационный алгоритмы решения задачи. Определить, какое количество членов ряда необходимо просуммировать для достижения указанной точности (сравнить результат суммирования со значением стандартной функции). Сравнить время выполнения алгоритмов, используя стандартную функцию GetTime модуля Dos

F(x)

 

Диапазон аргумента

Arctg(x)

|x|<1

 


Вариант 2

1. Написать подпрограмму вычисления  для заданного значения k.

2. Заданы: значение х, точность e. Составить подпрограмму расчета функции F(x) с точностью e, используя рекурсивный и итерационный алгоритмы решения задачи. Определить, какое количество членов ряда необходимо просуммировать для достижения указанной точности (сравнить результат суммирования со значением стандартной функции). Сравнить время выполнения алгоритмов, используя стандартную функцию GetTime модуля Dos.

F(x)

 

Диапазон аргумента

Arcth(x)

|x|<1

Вариант 3

1. Дано натуральное число n. Найти (2n)! и 2n!!. Использовать рекурсивную функцию вычисления факториала.

2. Заданы: значение х, точность e. Составить подпрограмму расчета функции F(x) с точностью e, используя рекурсивный и итерационный алгоритмы решения задачи. Определить, какое количество членов ряда необходимо просуммировать для достижения указанной точности (сравнить результат суммирования со значением стандартной функции). Сравнить время выполнения алгоритмов, используя стандартную функцию GetTime модуля Dos.

F(x)

 

Диапазон аргумента

X<1

Вариант 4

1. Даны натуральные числа n,m. Найти наибольший общий делитель НОД(n,m). Использовать рекурсивную функцию вычисления НОД, основанную на соотношении НОД (n,m)=НОД (m,r), где r - остаток от деления n на m

2. Заданы: значение х, точность e. Составить подпрограмму расчета функции F(x) с точностью e, используя рекурсивный и итерационный алгоритмы решения задачи. Определить, какое количество членов ряда необходимо просуммировать для достижения указанной точности (сравнить результат суммирования со значением стандартной функции). Сравнить время выполнения алгоритмов, используя стандартную функцию GetTime модуля Dos.

F(x)

 

Диапазон аргумента

 


Вариант 5

1. Составить рекурсивную подпрограмму расчета чисел Фибоначчи U(n), которые определяются следующим образом:

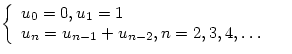$\left\{ \begin{array} {ll} u_0=0,u_1=1&\\ u_n=u_{n-1}+u_{n-2},n=2,3,4,\ldots &\end{array}\right.$.

2. Заданы: значение х, точность e. Составить подпрограмму расчета функции F(x) с точностью e, используя рекурсивный и итерационный алгоритмы решения задачи. Определить, какое количество членов ряда необходимо просуммировать для достижения указанной точности (сравнить результат суммирования со значением стандартной функции). Сравнить время выполнения алгоритмов, используя стандартную функцию GetTime модуля Dos.

F(x)

 

Диапазон аргумента

Вариант 6

1. Даны неотрицательные целые числа n и m. Составить рекурсивную подпрограмму вычисления

функции Аккермана: 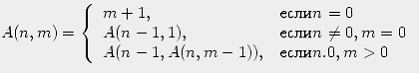$A(n,m)=\left\{ \begin{array} {ll} m+1,&если n=0\\ A(n-1,1),&если n\ne0,m=0\\ A(n-1,A(n,m-1)),&если n.0,m\gt\end{array}\right.$

Тестовые примеры:$A(1,b)=b+2,A(2,b)=2^b+3,A(3,b)=2^{b+3}-3.$

2. Заданы: значение х, точность e. Составить подпрограмму расчета функции F(x) с точностью e, используя рекурсивный и итерационный алгоритмы решения задачи. Определить, какое количество членов ряда необходимо просуммировать для достижения указанной точности (сравнить результат суммирования со значением стандартной функции). Сравнить время выполнения алгоритмов, используя стандартную функцию GetTime модуля Dos.

F(x)

 

Диапазон аргумента

Sin(x)

|x|<µ

 


Вариант 7

1 Вычислить, используя рекурсию значение функции при заданном n. Знаки перед корнями периодически повторяются группами (по три):"-","+","+".

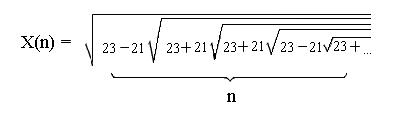
2. Заданы: значение х, точность e. Составить подпрограмму расчета функции F(x) с точностью e, используя рекурсивный и итерационный алгоритмы решения задачи. Определить, какое количество членов ряда необходимо просуммировать для достижения указанной точности (сравнить результат суммирования со значением стандартной функции). Сравнить время выполнения алгоритмов, используя стандартную функцию GetTime модуля Dos.

F(x)

 

Диапазон аргумента

cos(x)

|x|<µ

Вариант 8

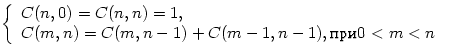1. Описать рекурсивную функцию C(m,n)$(0\leqslant m\leqslant n)$ для вычисления биноминального коэффициента по формуле: $\left\{ \begin{array} {ll} C(n,0)=C(n,n)=1,&\\ C(m,n)=C(m,n-1)+C(m-1,n-1), при 0<m<n&\end{array}\right.$для заданных m, n.

2. Заданы: значение х, точность e. Составить подпрограмму расчета функции F(x) с точностью e, используя рекурсивный и итерационный алгоритмы решения задачи. Определить, какое количество членов ряда необходимо просуммировать для достижения указанной точности (сравнить результат суммирования со значением стандартной функции). Сравнить время выполнения алгоритмов, используя стандартную функцию GetTime модуля Dos.

F(x)

 

Диапазон аргумента

|x|<µ

Вариант 9

1 Вычислить, используя рекурсию, значение функции

Х(n)= 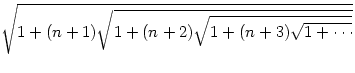$\sqrt{1+(n+1)\sqrt{1+(n+2)\sqrt{1+(n+3)\sqrt{1+\cdots при заданном значении n.

2. Заданы: значение х, точность e. Составить подпрограмму расчета функции F(x) с точностью e, используя рекурсивный и итерационный алгоритмы решения задачи. Определить, какое количество членов ряда необходимо просуммировать для достижения указанной точности (сравнить результат суммирования со значением стандартной функции). Сравнить время выполнения алгоритмов, используя стандартную функцию GetTime модуля Dos.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10