Геоинформационные системы в транспортной логистике (стр. 3 )

Для решения задачи коммивояжера в проектируемой системе было решено использовать генетический алгоритм. Он позволяет относительно быстро получить решения хорошего качества, несложен в реализации и легко допускает некоторые изменения постановки задачи (в частности, позволяет ввести в задачу коммивояжера использование ограничений по временному графику доставки заказов).

Идея генетических алгоритмов заимствована у живой природы и состоит в организации эволюционного процесса, конечной целью которого является получение оптимального решения в сложной комбинаторной задаче. Разработчик генетических алгоритмов выступает в данном случае как "создатель", который должен правильно установить законы эволюции, чтобы достичь желаемой цели как можно быстрее.

Генетические алгоритмы (ГА) — это адаптивные методы поиска, основанные на генетических процессах биологических организмов: биологические популяции развиваются в течение нескольких поколений, подчиняясь законам естественного отбора по принципу "выживает наиболее приспособленный" (survival of the fittest). Те особи, которые наиболее приспособлены к окружающим условиям (решения, обладающие наилучшим значением целевой функции), будут иметь относительно больше шансов воспроизвести потомков. Слабо приспособленные особи либо совсем не произведут потомства, либо их потомство будет очень малочисленным. Это означает, что гены от высоко адаптированных или приспособленных особей будут распространяться в увеличивающемся количестве потомков на каждом последующем поколении. Комбинация хороших характеристик от различных родителей иногда может приводить к появлению потомка, чья приспособленность больше, чем приспособленность любого из его родителей. Таким образом, вид развивается, лучше и лучше приспосабливаясь к среде обитания.

Вначале для решения любой задачи с помощью ГА должен быть разработан метод кодирования решений. Закодированное решение называют хромосомой. Каждый атомарный элемент в хромосоме, несущий в себе значимую информацию, называется геном.

Для хромосом также имеется некая функция приспособленности или фитнес-функция (от англ. Fitness ) которая определяет численное значение годности хромосом для данной задачи.

На начальном этапе случайным образом генерируется достаточно большая популяция данного вида хромосом и вычисляется приспособленность особей в ней. Далее циклически повторяется следующий процесс: некоторым образом из популяции отбираются пары особей-решений и скрещиваются, данная операция называется кроссовер (crossover). Решения-потомки добавляются в популяцию, обычно взамен наиболее плохих решений. Для того чтобы не зависеть от возможной ограниченности базового набора хромосом и неспособности на их основе построить оптимальную хромосому, используют мутации. Таким способом получают совершенно новые хромосомы. Естественно, чтобы мутации не мешали процессам целенаправленной селекции, их применяют достаточно редко (с вероятностью порядка 1%, конкретная величина определяется опытным путем). Далее цикл повторяется. Критерием останова в генетическом алгоритме может служить нахождение точного решения, если это возможно определить (например, при поиске корней уравнения), выполнение заданного количества итераций или постоянство наилучшего найденного решения в течение некоторого количества итераций.

В качестве метода кодирования решения в хромосому было решено использовать путевое представление.

Путевое представление — наиболее естественное представление рейса. Например, рейс 5–1–7–8–9–4–6–2–3, где каждая цифра представляет собой идентификатор заказа, представлен просто как2 3).

В качестве кроссовера можно использовать частично отображенный кроссовер— partially-mapped crossover (PMX) .

PMX (partially-mapped crossover) строит потомков, выбирая сегмент из рейса одного из родителей и совершая перестановки генов, пока этот сегмент не становится идентичным соответствующему сегменту второго родителя. Сегмент маршрута выбирается двумя случайными точками разреза. Например, два родителя (разрезы отмечены " | ")

Р1 =| | 8 9) и

Р2 =| | 9 3)

могут получить потомков следующим способом. Во-первых, сегменты между точками обреза меняются местами (символом "x" обозначается неизвестный символ).

П1 = (х х х | | х х) и

П2 = (х х х | | х х)

также этот обмен определяет серию преобразований данных: 1 <‑> 4, 8 <‑> 5, 7 <‑> 6 и 6 <‑> 7. Теперь можно заполнить остальные города, для которых нет конфликтов:

П1 = (х 2 3 | | x 9) и

П2 = (х x 2 | | 9 3).

Наконец, первый "х" из потомка П1 (который должен был быть 1, но был обнаружен конфликт) заменяется на 4 (см. серию преобразований данных). Таким же образом, второй "х" из потомка П1 меняем на 5; в потомке П2 меняем "х" на 4 и 5 соответственно. Получим:

П1 =| | 5 9) и

П2 =| | 9 3).

В качестве мутации можно использовать замену двух участков маршрута.

Например из родителя

Р1 = (1 2 3 4 5 6 7 8 9)

можно получить потомка

П1 =3 9)

Заменив в нем участки маршрутаи

На последнем предварительном этапе необходимо создать начальную популяцию. В популяции вполне могут присутствовать случайные маршруты. Это не ухудшает работу алгоритма, и в то же время позволяет избежать быстрой сходимости всей популяции к какому-то отдельному решению.

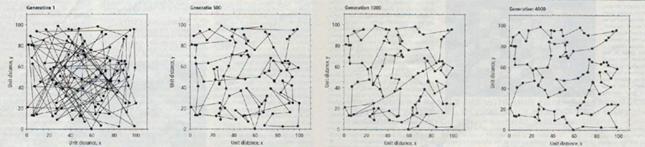
 Рис.4 : Генетический алгоритм использовался при решении задачи коммивояжера на 100 городов. В начале генерировалась начальная популяция, состоящая из 100 случайных решений, из них при помощи мутации и кроссовера создавались 100 потомков. Таким образом, получалось 200 решений. 100 лучших решений выбирались для следующей популяции. Лучшие решения после 500, 1000 и 4000 итераций показывают процесс улучшения качества решений. Улучшение качества решений на каждом из последующих этапов эволюции заметно невооруженным взглядом (программу, решающую подобный пример, можно найти в разделе публикаций на сайте www. ).
  Эволюционный алгоритм, просмотрев относительно небольшое количество решений, нашел достаточно неплохое. Возможно это и не лучшее решение, но оно достаточно высокого качества. Было просмотрено всего около 400000 решений, т. е. одно из 210150 всех возможных решений.

При необходимости учёта временных ограничений на доставку заказов, требуется изменить фитнес-функцию таким образом, чтобы опоздание доставки заказа наказывалось дополнительным штрафом.

Решение задачи планирования доставки грузов (ЗПДГ)

Задача планирования доставки грузов отличается от задачи коммивояжера тем, что для доставки заказов мы имеем не одну, а несколько автомашин заданной грузоподъемности. Используя их, необходимо развести все заказы со склада таким образом, чтобы минимизировать количество использованных машин и суммарную длину пробега.

Для решения ЗПДГ было решено использовать “лепестковый алгоритм”. Этот метод относительно несложен и в то же время позволяет быстро получить решение, близкое к оптимальному.

Предполагается, что склад лежит в центре декартовой прямоугольной системы координат.

В начале каждому заказу Ki сопоставляется полярный угол φi, образуемый отрезком Заказ - Склад с воображаемой осью OX

φi = arctg((Yi-Y0)/(Xi-X0)),

где (X0; Y0) - координаты склада, а (Xi; Yi) - координаты заказа

После этого все заказы упорядочиваются по полярному углу и в порядке образованной очереди начинают формировать рейсы - на каждую автомашину последовательно из общей очереди добавляются заказы до тех пор, пока машина не переполнится.

В результате рейсу, на котором лежат заказы Ki, Ki+1,….Kj соответствует свой сектор φi ^ φj, причем сектора разных рейсов не пересекаются. Далее внутри каждого рейса решается задача коммивояжера и получаются рейсы в виде характерной "ромашки" (Рис. ).

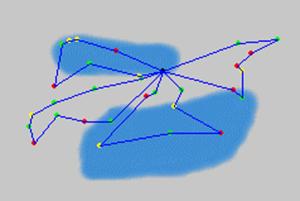
Рис.5. Иллюстрация к методу построения рейсов по полярному углу

Как уже было сказано, у данного метода построения рейсов есть много плюсов - он прост, дает решение хорошего качества, к тому же можно легко ввести понятие соседних по полярному углу рейсов и при дальнейшей оптимизации учитывать степень близость рейсов.

К сожалению, данный алгоритм не дает гарантии построения решений с учетом временного графика, хотя позволяет строить приемлемые решения для задач, в которых заказы имеют большие временные окна.

Вариант многие ко многим представляет собой самый интересный и в то же время самый сложный случай. Сложность данной задачи заключается в том, что не определена более, или менее стандартная постановка данной задачи. В каждой компании, занимающейся перевозками с применением данной схемы, есть свой набор правил, на основании которых осуществляется планирование рейсов. Правила эти для каждой компании во многом уникальны, и редко полностью формализованы. Иными словами, крайне сложно выделить некую общую постановку задачи и общий алгоритм ее решения. Разрабатывать же общий алгоритм нецелесообразно, ибо при внедрении его в конкретную компанию, затраты на доработку реализованного варианта задачи до требуемого сопоставимы с затратами на разработку и программную реализацию системы планирования доставки заказов “с нуля”.

В качестве примеров постановки задачи многие ко многим можно привести пример классической транспортной задачи. Эта постановка предполагает, что для заказчика неважно, с какого именно склада к нему будет доставлена готовая продукция. Классическое применение данной постановки – развоз бетона или асфальта от нескольких производящих их заводов к стройкам, идущим в различных городах. При этом предполагается, что затраты единицы продукции зависят только от расстояния между заводом и пунктом разгрузки. Также подразумевается, что каждая машина постоянно курсирует между выбранным заводом и пунктом разгрузки.

Гораздо более сложной для решения (с комбинаторной точки зрения) задачей является случай, когда необходимо перевезти конкретные заказы с одного места на другое. Дело в том, что при решении на практике этой не очень сложной на первый взгляд задачи могут обнаруживаться самые различные ограничения.

Иногда, заказы некоторого типа можно доставлять лишь в определенной последовательности, которая зависит от типа используемого автотранспорта. Например, в некоторые фуры, с одним выходом из фургона, загрузка и погрузка товара осуществляется только как в стек, то есть заказы можно разгружать строго в последовательности, обратной той, в которой они были погружены. Некоторые машины, с двумя входами могут одновременно работать как стек и очередь, позволяя производить погрузку с одной стороны, а разгрузку с двух сторон. Кроме того, возможны особенности кузова или тары, в которой поставляются заказы, которые позволяют осуществить произвольный доступ к размещенным в кузове заказам.

Кроме вышесказанного, следует учитывать, что некоторые заказы могут быть принципиально доставлены только определенным подмножеством машин, а некоторые заказы могут поступать в отдел планирования уже после начала объезда заказов и требуют добавления на один из уже спланированных рейсов в режиме реального времени.

По вышеописанным причинам, каждая конкретная реализация задачи планирования доставки заказов по схеме “многие ко многим” должна быть рассчитана под конкретного заказчика и учитывать особенности его предметной области. Заранее проводить реализацию подобной задачи в рамках проектируемой логистической программы можно лишь подразумевая ее использование в демонстрационных целях.

5) Концепция блока по оценке экономических издержек производства транспортных услуг

Обратимся к классификации затрат АТП, приведенной в вводной части работы:

1) материальные затраты

2) затраты на оплату труда

3) отчисления на социальные нужды

4) прочие затраты

В состав материальных затрат включаются затраты на:

1) топливо

2) смазочные и эксплутационные материалы

3) запасные части и материалы

4) агрегаты

5) шины

6) прочие материальные затраты.

Рассмотрим перечень материальных затрат более подробно:

1) топливо

В нижеприведенной таблице приведены данные эксплуатационных испытаний наиболее массовых автомобилей, используемых при внутригородских перевозках. (данные по [2])

В результате обработки статистических данных (по данным [2]), была получена эмпирическая формула для расчета расходов на топливо:

(*)

где - расчетная стоимость топлива за маршрут,

- обобщенный коэффициент, учитывающий надбавки и снижения в расходе топлива при движении в различных условиях

a- линейная норма расхода топлива на пробег автомобиля без груза, л/100 км

K- коэффициент, зависящий от марки и модели автомобиля

-масса груза между пунктами назначения, т

- цена 1л топлива

- пробег автомобиля между пунктами назначения, км

Рассмотрим вышеуказанное выражение более подробно:

1) характеризует режим и характер движения ( плотное городское, трасса, пересеченная местность). Этот коэффициент может варьироваться от 1 (трасса) до 1,4 (пересеченная местность).

2) Параметр a основан на данных производителя.

3) Параметр К характеризует зависимость расхода топлива от загрузки для конкретной марки и модели автомобиля. В данной спецификации эта зависимость для упрощения принимается линейной.

Данное выражение было получено автором по выборке крупного АТП (325 машин в течение 2х лет) по методологии [4], используя метод наименьших квадратов.

Стоит заметить, что приведенный формула (*) не всегда удобна для расчетов, так как часто возникает проблема с данными по загрузке и пробегах автомобилей между пунктами назначения на маршруте, более того данный априорный метод оценки не является прецизионно точным, поэтому более удобной для оценки является :

Где - пробег автомобиля между пунктами назначения, км

- средневзвешенная масса груза, определяется характером развозок (например, в один из пунктов назначения большая часть груза или равномерное распределение груза по пунктам назначения.)

Безусловно, приведенные данные являются усредненными, и оценка, полученная с их помощью, является весьма приближенной. Более точные оценки могут быть получены с помощью повторной калибровки по реальным данным, полученным из исследуемого АТП.

2) Затраты на смазочные материалы.

Согласно [4], расходы на смазочные материалы у автомобилей зарубежного производства составляют от 2,5 до 6 % от стоимости топлива, от 4,5 до 8 % у автомобилей отечественного производства.

3) Затраты на ТО и ремонт

В приведенной ниже таблице представлены данные по затратам на ТО и ремонт европейских автомобилей.

Затраты на ТО и ремонт европейских автомобилей

Приведенные величины могут быть использованы для приближенной оценки затрат на ТО и ремонт автомобилей зарубежного производства, эксплуатирующихся в отечественных АТП, но при этом значения удельных затрат должны быть увеличены на 15-20%.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4