Методика обучения математике студентов гуманитарных специальностей вузов в контексте интенсификации обучения

На правах рукописи

Дмитриева Мария Николаевна

Методика обучения математике студентов гуманитарных специальностей вузов в контексте интенсификации обучения

13.00.02 — теория и методика обучения и воспитания (математика)

Автореферат

диссертации на соискание учёной степени

кандидата педагогических наук

Саранск 2011

Работа выполнена на кафедре психологии, педагогики и дисциплин начального образования Государственного образовательного учреждения высшего профессионального образования «Тульский государственный педагогический университет имени Л. Н. Толстого»

Научный руководитель: доктор педагогических наук, профессор

Официальные оппоненты: доктор педагогических наук, профессор

кандидат педагогических наук, доцент

Ведущая организация: ГОУ ВПО «Московский педагогический государственный университет»

Защита состоится «29» июня 2011 г. в 13 часов на заседании диссертационного совета ДМ 212.118.01 по защите докторских и кандидатских диссертаций при ГОУ ВПО «Мордовский государственный педагогический институт имени М. Е. Евсевьева» Республика Мордовия, г. Саранск, а, ауд. 320.

С диссертацией можно ознакомиться в библиотеке ГОУ ВПО «Мордовский государственный педагогический институт имени »

Автореферат разослан и размещен на сайте www. *****

« 26 » мая 2011 г.

Ученый секретарь

диссертационного совета

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность исследования. Современная модернизация российского образования имеет приоритетными направлениями фундаментальность, гуманизацию, гуманитаризацию и информатизацию. Понимание необходимости широкого общекультурного образования специалистов привело к введению в 1995 году ГОС ВПО обязательной дисциплины «Математика и информатика» для студентов всех гуманитарных специальностей вузов. Это нововведение потребовало разработки проблем математического образования специалистов гуманитарного профиля.

Анализ литературы и опыта преподавания свидетельствует, что студенты гуманитарных специальностей имеют разные по уровню знания по математике; у них, как правило, отсутствует интерес к ее изучению. В то же время для многих гуманитарных специальностей ряд математических знаний и способов деятельности носит профессионально значимый характер. Например, знание основ математической логики, теории вероятностей, математической статистики, способов решения задач из этих разделов математики крайне важно для будущих филологов. Несмотря на различие специальностей, для всех гуманитариев необходимо умение анализировать информацию, выделять суть вопроса, владеть логикой рассуждений, обобщать статистический материал, правильно интерпретировать ситуацию. Все эти качества развиваются в процессе изучения математики, на который, однако, отводится очень мало времени - в среднем 36 часов. С введением ФГОС роль этого негативного фактора возрастает, поскольку указывается число зачетных единиц, приходящихся на целый блок дисциплин, и к математике на отдельных факультетах подходят по остаточному принципу. Как преподавать в этих условиях математику, обеспечивая достижение поставленных целей?

Анализ литературы по теории и методике обучения математике показал, что существуют два основных подхода к конструированию курса математики для гуманитарных специальностей. Смысл первого из них заключается в знакомстве студентов с основными направлениями математики, представленными в виде обзорного общеобразовательного курса (Н. Х. Розов, Е. В. Шикин и др.). В основе другого подхода лежит адаптация полного математического курса к предполагаемому уровню подготовки студентов и реализация профессиональной направленности обучения (Г. Л. Луканкин и др.). В русле данного подхода выполнены исследования Т. А. Гавазы, Н. А. Дергуновой, А. А. Соловьевой и др. Однако этим подходам присущи недостатки: первый – не учитывает профессиональные потребности гуманитариев, второй – требует много времени для усвоения и достаточно высокий уровень математической подготовки, не свойственный большей части студентов-гуманитариев.

Отдельные вопросы обучения математике студентов гуманитарных факультетов изложены в работах Д. Ф. Богатова, В. И. Михеева, Н. Х. Розова, и др., а также в кандидатских диссертациях С. И. Бордаченко, И. Д. Гайвазовой, А. Д. Ивановой, И. П. Мединцевой, Н. В. Набатниковой, С. В. Поморцевой, А. А. Соловьевой и др. Несмотря на значимость данных и указанных выше работ для исследования проблемы математической подготовки студентов-гуманитариев, в них отсутствует комплексное исследование, основанное на идее интенсификации обучения.

Действительно, краткие временные рамки учебных курсов для гуманитариев делают очевидным, что достичь успеха в решении названной выше проблемы можно только посредством интенсификации обучения математике.

Смысл интенсификации обучения заключается в решении двух взаимосвязанных задач: повышение качества обучения и одновременное снижение временных затрат. В качестве путей интенсификации предлагается использовать: активизирующие средства, формы и методы обучения ( и др.); повышение информативной емкости содержания материала обучения, применение интенсивного контроля знаний с осуществлением обратной связи и усилением мотивации учения ( и др.).

Вопросам интенсификации обучения математике и информатике посвящены работы И. В. Гончаровой, Е. В. Клименко, Н. И. Миндорова, Н. В. Мясоедовой, В. Т. Петровой, Т. В. Рыбаковой, С. С. Тасмуратовой и др. В последние пять лет актуальность исследования интенсификации обучения стали связывать с новыми информационными технологиями, электронными средствами поддержки обучения в системе дистанционного образования (, , и др.). Однако в этих работах акцент сделан на содержание обучения, не исследуются возможности интенсификации в направлении комплексного использования специальных средств (учебно-методические комплексы, профессионально-ориентированные задания, средства мультимедиа), развития профессионально значимых видов мышления (логического и стохастического) и формирования приемов самообразования, применения методико-математических средств уплотнения учебной информации.

В настоящее время все больше внимания уделяется разработке вариативных, разноуровневых, личностно-ориентированных учебных программ, учитывающих индивидуальные особенности обучаемых. В качестве специфики мышления студентов гуманитарных специальностей выделяют (Н. Х. Розов и др.) приоритет ассоциативного над формально логическим, сильную эмоциональную окрашенность, приоритет конкретного над абстрактным, неустойчивость внимания. Ясно, что этот фактор оказывает влияние на процесс обучения математике студентов гуманитарных специальностей.

В работах , , С. Д. Смирнова, И. Э. Унт, Р. А. Утеевой и др. изложены принципы, пути и средства индивидуализации и дифференциации обучения в высшей и средней школе. Влияние индивидуальных психологических особенностей гуманитариев в процессе обучения математике показано в работах таких известных психологов, педагогов и методистов, как , Т. А. Иванова, Г. Л. Луканкин, , и др. Однако эти исследования были выполнены либо на базе школьной математики без учеты вузовской специфики, либо вне контекста интенсификации обучения.

Таким образом, на современном этапе развития вузовского образования в обучении математике студентов гуманитарных специальностей выявлены существенные противоречия между:

– все большим проникновением математических технологий в гуманитарные науки и низкой мотивацией студентов гуманитарных специальностей изучения математики;

– необходимостью индивидуализации обучения студентов гуманитарных специальностей в силу их разных способностей, интересов, довузовской подготовки по математике и отсутствием соответствующих научно-обоснованных в контексте интенсификации обучения дидактических и методических средств;

- уменьшением аудиторного времени с одновременным увеличением самостоятельной работы студентов по математике гуманитарного профиля и низким уровнем сформированности навыков самостоятельной деятельности студентов.

Обнаруженные противоречия определяют актуальность и обуславливают выбор темы настоящего исследования, проблема которого заключается в выявлении и реализации путей совершенствования методики обучения математике студентов гуманитарных специальностей вузов в контексте интенсификации обучения.

Цель исследования – разработать методическую систему обучения математике студентов гуманитарных специальностей вузов в контексте интенсификации обучения и экспериментально проверить ее эффективность.

Объект исследования – процесс обучения математике студентов гуманитарных специальностей вузов.

Предмет исследования – цели, содержание, методы, формы и средства обучения математике студентов гуманитарных специальностей в контексте интенсификации обучения.

Гипотеза исследования: если учесть специфику содержания курса математики для гуманитарных специальностей вузов, определить и использовать приемы и средства интенсификации обучения математике, основанные на принципе профессиональной направленности обучения и обусловленные психолого-педагогическими особенностями студентов гуманитарных специальностей, обеспечить дидактическими контрольно-измерительными материалами, разноуровневыми заданиями и разработать мониторинг процесса обучения математике по установленным показателям (уровень мотивации к изучению математики и уровень математической подготовки), то качество математической подготовки студентов гуманитарных специальностей повысится.

В соответствии с объектом, предметом, целью и выдвинутой гипотезой исследования были поставлены следующие задачи:

1. Провести анализ педагогической, методической и психологической литературы и выявить условия интенсификации обучения математике студентов гуманитарных специальностей вузов, в частности бакалавров по направлениям «филология» и «юриспруденция».

2. Разработать методическую систему обучения математике студентов гуманитарных специальностей вузов в контексте интенсификации обучения с учетом их довузовской подготовки, психологических особенностей и профессиональной направленности.

3. Выделить в содержании курса математики профессионально важные для филологов и юристов разделы. Разработать к ним систему дифференцированных заданий с профессионально-прикладным содержанием и контрольно-измерительные материалы.

4. Экспериментально проверить эффективность разработанной методики обучения математике студентов гуманитарных специальностей в контексте интенсификации обучения.

Научно-теоретическими предпосылками исследования послужили: концепция деятельностного подхода к обучению; технологический подход к обучению; исследования, направленные на выявление психолого-педагогических особенностей обучающихся; труды по теории и методике обучения математике (С. П. Амутнова, В. А. Гусев, В. А. Далингер, И. В. Егорченко, И. В. Дробышева, М. И. Зайкин, Е. И. Санина, Л. С. Капкаева, Ю. М. Колягин, Л. Д. Кудрявцев, Н. И. Мерлина, В. И. Михеев, А. Г. Мордкович, В. Т. Петрова, М. А. Родионов, Г. И. Саранцев, В. А. Тестов, Р. А. Утеева, И. В. Харитонова и др.).

Для решения поставленных задач использовались следующие методы исследования: системный анализ; деятельностный подход; анализ психолого-педагогической и научно-методической литературы и диссертаций по проблеме исследования; анализ ГОС ВПО, программ и учебных пособий по математике для вузов; изучение и обобщение педагогического опыта; наблюдение, тестирование, анкетирование, беседа; педагогический эксперимент; статистическая обработка и анализ результатов эксперимента.

Экспериментальная база исследования – Рязанский государственный медицинский университет им. академика И. П. Павлова и Рязанский институт (филиал) Московского государственного открытого университета.

Решение задач исследования осуществлялось в несколько этапов.

На первом этапе ( гг.) определялись направления исследования; анализировалась психолого-педагогическая и научно-методическая литература по теме исследования, обобщался опыт обучения математике студентов гуманитарных специальностей; осуществлялся констатирующий этап эксперимента.

На втором этапе ( гг.) вырабатывались основные положения методики обучения математике студентов гуманитарных специальностей в контексте интенсификации обучения; разрабатывались методические материалы; проводилась экспериментальная апробация предложенной методики; осуществлялся поисковый этап эксперимента.

На третьем этапе ( гг.) проводилась опытно-экспериментальная проверка эффективности методики обучения математике студентов гуманитарных специальностей в контексте интенсификации обучения; осуществлялись анализ, обобщение и систематизация результатов экспериментальной работы, уточнялись выводы, оформлялся текст диссертационного исследования.

Научная новизна исследования заключается в том, что проблема повышения качества обучения математике студентов гуманитарных специальностей высших учебных заведений решается на основе интенсификации обучения, реализуемой путем комплексного использования условий, приемов и средств интенсификации обучения, учитывающих специфику содержания курса математики и психолого-педагогические особенности студентов гуманитарных специальностей. Такой подход позволил разработать методику обучения математике студентов гуманитарных специальностей, предусматривающую использование знаково-символьного представления учебной информации, информационно-коммуникативных технологий и направленную на развитие логической и стохастической составляющих мышления и навыков самообразования студентов.

Теоретическая значимость исследования заключается в том, что

– выявлены условия интенсификации обучения математике студентов гуманитарных специальностей;

– разработаны приемы и средства интенсификации обучения математике студентов гуманитарных специальностей;

– выявлены профессионально значимые компоненты мышления, характерные для специалистов-гуманитариев, и разработаны приемы их формирования;

– определены требования к составлению и подбору заданий, реализующих интенсификацию обучения математике студентов гуманитарных специальностей (доступность, профессиональная направленность, дозирование помощи в решении задач, составление инструкций и алгоритмов решения задач, наличие исследовательских заданий и др.).

Практическая значимость исследования заключается в том, что разработанная методика формирования математических понятий и решения задач для студентов специальностей «филология» и «юриспруденция», набор дидактических материалов (методические пособия, дифференцированные задания, тестовые, контрольные задания, лабораторные работы с использованием информационных технологий) могут быть использованы в практике преподавания математики студентам гуманитарных специальностей, а также для формирования учебно-методических комплексов.

Результаты работы открывают перспективу дальнейшего исследования интенсификации обучения математике студентов других специальностей, а также обеспечения и повышения уровня методической подготовки преподавателей к реализации такой методики обучения математике в вузах.

Достоверность и научная обоснованность результатов исследования обеспечиваются опорой на теоретические разработки в области педагогики, психологии, методики преподавания математики, адекватностью методов исследования целям работы, сочетанием качественного и количественного анализа результатов эксперимента, включая применение методов математической статистики.

Основные положения, выносимые на защиту:

1. Эффективность математической подготовки студентов гуманитарных специальностей в контексте интенсификации обучения обеспечивается представлением о математике как гуманитарной науке, развитием профессионально-значимых логической и стохастической составляющих мышления студентов, применением специфического представления (знаково-символьного) учебного материала.

2. Основными условиями интенсификации обучения, обеспечивающими повышение качества обучения математике студентов гуманитарных специальностей, являются:

- формирование положительной мотивации изучения математики;

- развитие у студентов логического мышления;

- преемственность в обучении математике и межпредметные связи;

- дифференцированный подход к обучению;

- наглядность (моделирование) учебного материала;

- применение информационных средств и технологий обучения.

Основными приемами и средствами интенсификации обучения, обеспечивающими повышение качества обучения математике студентов гуманитарных специальностей являются:

- предъявление учебного материала крупными блоками;

- использование знаково-символьного представления учебного материала;

- создание проблемных учебных ситуаций;

- организация работы студентов в малых группах.

К средствам интенсификации обучения математике относятся дифференцированные профессионально-ориентированные задания, проблемные учебные ситуации, учебные проекты, информационные технологии.

3. Мониторинг качества обучения математике студентов гуманитарных специальностей представляет собой диагностику психологических особенностей студентов (соционический тип личности, мышление, память и пр.), оценку уровня усвоения ими учебного материала и уровня мотивации к изучению математики и осуществляется с использованием информационных средств и технологий, наблюдений, опросов, тестов, анкет, дифференцированных заданий по математике.

4. Основные требования к разработке комплекса разноуровневых дифференцированных заданий в контексте интенсификации обучения математике:

- доступность;

- профессионально-ориентированность;

- дозирование подсказок и алгоритмов решения задач;

- постановка исследовательских заданий и проблемных ситуаций;

- стимулирование повышения студентами уровня усвоения материала.

Апробация результатов исследования осуществлялась в виде докладов на Международных научных и научно-практических конференциях «Образование, наука и экономика в вузах на рубеже тысячелетий» (Словакия, 2000), «Функциональные пространства. Дифференциальные операторы. Проблемы математического образования» (Москва, 2003), «Проблемы развития личности: психологическое консультирование и психотерапия» (Рязань, 2008), «Образование, наука и экономика в вузах. Интеграция в международное образовательное пространство» (Польша, 2008), на Всероссийских научно-практических конференциях «Математика и общество. Математическое образование на рубеже веков» (Дубна, 2000), «Актуальные проблемы обучения математике» (Орёл, 2002), «Современные информационные технологии в образовании» (Рязань, 2002), по проблемам математики, информатики, физики, химии и методике преподавания естественнонаучных дисциплин (Москва, , 2010), «Наука в вузах: математика, физика, информатика. Проблемы высшего и среднего профессионального образования» (Москва, 2009), на межрегиональных научно-практических конференциях «Проблемы развития личности» (Рязань, ), «Воспитательная работа в ВУЗе: задачи, проблемы, пути решения» (Рязань, 2008), на научно-практических семинарах ФПО МГУ «Психолого-педагогические и методические вопросы образования» (Москва, 2009), МГОУ «Передовые идеи в преподавании математики в России и за рубежом» (Москва, 2010), Мордовского государственного педагогического института (Саранск, 2011).

Структура диссертации. Диссертация состоит из введения, двух глав, заключения, библиографического списка, приложений, иллюстрирована таблицами и рисунками.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность темы исследования; сформулированы его проблема, цель, объект, предмет, гипотеза и задачи; раскрыты методологические и теоретические основы, методы исследования, описаны его этапы; дана характеристика научной новизны, теоретической и практической значимости; сформулированы основные положения, выносимые на защиту.

Первая глава диссертации посвящена теоретическим основам обучения математике студентов гуманитарных специальностей вузов в контексте интенсификации обучения. Анализ педагогической, методической и специальной литературы по проблеме иссследования позволил сделать следующие выводы: студенты гуманитарных специальностей изучают не отдельный математический курс, а интегрированный - «Математика и информатика»; существуют два основных подхода к конструированию курса математики для студентов-гуманитариев, один из которых носит характер обзорного общеобразовательного курса, а другой представляет собой адаптированный с учетом специфики будущей профессиональной деятельности классический курс высшей математики; ГОС ВПО по сути одинаков для всех специальностей гуманитарного профиля и вместе с рабочими программами предполагает изучение большого по объему и трудного для усвоения учебного материала в условиях ограниченного бюджета учебного времени и отсутствия соответствующего методического обеспечения.

Названным выше подходам присущи недостатки: первый неполно реализует профессиональную направленность математической подготовки гуманитариев, второй – требует много времени для усвоения и определенную базовую подготовку студентов.

Кроме того, выявлено, что отдельные гуманитарные специальности («филология» и «юриспруденция») требуют различных математических знаний и умений, видов мышления (логического, стохастического), способов обработки информации. Однако большинство студентов имеют низкую мотивацию изучения математики, разный уровень довузовской математической подготовки, слабо развитые навыки построения логических рассуждений и самостоятельной учебной работы при повышенном интересе к профессионально-значимому учебному материалу.

С целью изучения психолого-педагогических особенностей обучаемых было проведено тестирование студентов филологического и юридического факультетов Рязанского государственного медицинского университета на предмет определения их соционических типов. Его результаты свидетельствуют, что большинство опрошенных относятся к типам, у которых доминирует интуитивное и образное восприятие информации, что требует при обучении таких студентов использования специфических форм представления учебного материала.

Таким образом, налицо необходимость поиска нового подхода к обучению математике студентов гуманитарных специальностей, устраняющего названные выше недостатки и позволяющего реализовать цели, поставленные ГОС ВПО в условиях ограниченных временных рамок. Таким подходом является интенсификация обучения.

В ходе исследования выявлены условия, приемы и средства интенсификации обучения математике студентов специальностей гуманитарного профиля.

К условиям интенсификации обучения математике студентов гуманитарных специальностей относятся:

- формирование положительной мотивации изучения математики;

- развитие у студентов логического мышления;

- преемственность в обучении математике и межпредметные связи;

- дифференцированный подход к обучению;

- наглядность (моделирование) учебного материала;

- применение информационно-коммуникативных средств и технологий обучения.

Все указанные условия можно качественно реализовать лишь при комплексном использовании приемов и средств интенсификации обучения. С этой целью была построена методическая система обучения математике студентов гуманитарных специальностей в контексте интенсификации обучения (рис. 1), которая предполагает:

1. Выделение основных профессионально значимых разделов математического курса, использование в обучении внутрипредметных и межпредметных связей математики, ее общекультурного значения;

2. Создание в процессе обучения сочетания условий интенсификации обучения математике, ориентированных на индивидуально-психологические особенности студентов;

3. Использование в обучении системы дифференцированных заданий с дозированным включением профессионально-прикладного содержания, алгоритмов решения, индивидуальных и групповых творческих заданий;

4. Внедрение мониторинга процесса обучения математике по показателям: уровень мотивации к изучению математики, уровень математической подготовки.

Основными приемами интенсификации обучения, обеспечивающими повышение качества обучения математике студентов гуманитарных специальностей, являются:

- предъявление учебного материала крупными блоками;

- использование знаково-символьного представления учебного материала;

- создание проблемных учебных ситуаций;

- организация работы студентов в малых группах.

Эти приемы реализуются в процессе обучения путем использования специальных средств обучения. К средствам интенсификации обучения математике относятся дифференцированные профессионально-ориентированные задания, проблемные ситуации, учебные проекты, программно-педагогические средства, предполагающие использование информационнных технологий.

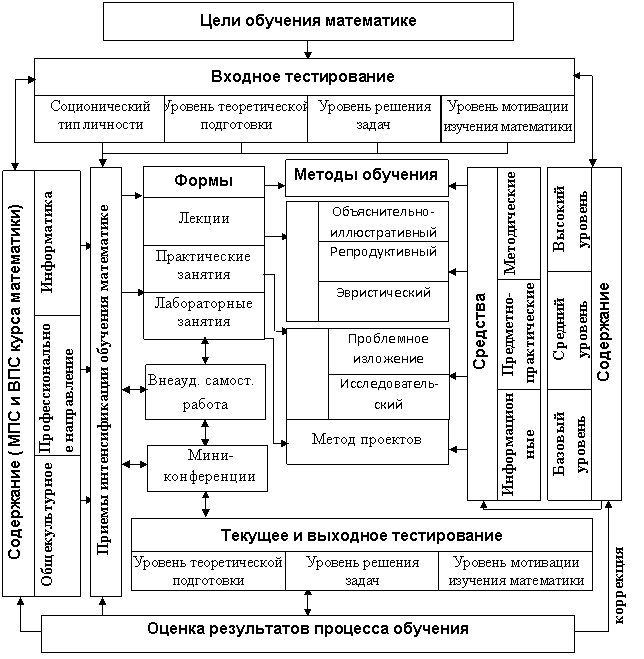
Рис.1 Методическая система «Обучения математике студентов гуманитарных специальностей вузов в контексте интенсификации обучения»

(МПС - межпредметные связи, ВПС – внутрипредметные связи)

Во второй главе диссертации представлена методика обучения математике студентов гуманитарных специальностей, разработанная в контексте интенсификации обучения. В ней показана реализация одновременно нескольких условий интенсификации обучения математике, доказана эффективность их применения на примере обучения математике студентов специальностей «филология» и «юриспруденция».

Наглядность и моделирование рассмотрены как важные условия интенсификации обучения математике студентов гуманитарных специальностей. В работе выделены следующие виды наглядности: фоновая (обеспечение положительной мотивации обучения), оперативная (использование рисунков, графиков, таблиц), структурная (отбор и дозировка материала, пропедевтика введения новых понятий, осуществление межпредметных связей), наглядность преемственности (ассоциативные связи внутри и между предметами). Показано, как названные виды наглядности, применяемые в комплексе, способствуют интенсификации обучения математике студентов гуманитарных специальностей. Осуществляемый при этом постепенный переход от наглядно-образного восприятия к символическому способствует развитию логического мышления студентов. За счет этого удается в дальнейшем не тратить аудиторное время на исправление ошибок в понимании студентами основных понятий, что дает возможность интенсифицировать процесс обучения математике.

В диссертационной работе выделены виды задач, направленные на формирование положительной мотивации студентов изучения математики. К ним относятся профессионально-ориентированные задачи; задачи, содержащие исторические данные, общекультурные факты; задачи, содержащие элементы проблемности. Разработанные профессионально-ориентированные задачи реализуют межпредметные связи математики с лингвистикой, криминалистикой, нумизматикой, а также информатикой. Использование информационных технологий позволяет упростить и автоматизировать решение многих математических задач, в том числе профессионально-ориентированных.

В работе показано, как одни и те же математические задачи могут обеспечивать выполнение одновременно несколько условий интенсификации обучения математике. Например, при изучении темы «Множества».

Задача 1. Сравнить на отношения (включение и равенства) множество заглавных букв русского языка и множество заглавных букв английского языка. Найти пересечение, объединение и разности этих множеств.

Решая эту задачу на практических занятиях, наглядными средствами (диаграмма, модель-алфавит) закрепляются и разъясняются понятия «множество», «подмножество», «операции на множествах». Предлагаемые в виде индивидуальных домашних заданий аналогичные задачи (с французским и немецким языками, множествами букв своего имени и отчества, достоинствами монет) способствуют формированию положительной мотивации изучения математики. Опыт показывает, что студенты увлекаются оперированием с известными им объектами, привыкая работать с математической символикой, действовать логически.

Эта же задача обеспечивает выполнение и других условий интенсификации обучения математике: реализации внутрипредметных и межпредметных связей, общекультурной составляющей обучения математике.

В процессе формирования понятия «Событие» в разделе «Основы теории вероятностей» преподаватель опирается на изученные ранее понятия теории множеств: диаграммы Эйлера применяются для представления различных видов событий и их взаимосвязей. В частности, иллюстрируются понятия противоположных, совместных и несовместных событий диаграммами Эйлера. Выстраивание аналогий с операциями над множествами (объединение, пересечение) позволяет изучить и закрепить более сложные понятия суммы и произведения событий.

Задача 2. Из двух множеств букв русского и английского языка в случайном порядке выбираем по одной. Найти вероятность появления одинаковых букв.

При решении этой задачи напоминают студентам, что в начале курса были рассмотрены множества букв русского и английского языков, их отношения и операции над ними. Тем самым осуществляем повторение понятий множества, сокращаем время на разработку их моделей.

Выстраивание последовательностей (цепочек) задач, связанных друг с другом по содержанию, позволяет интенсифицировать введение и освоение более сложных структур в курсе, экономя время на их определениях в будущем и расширяя модели новых понятий. Приведем пример такой цепочки.

Задача 3. При бросании игральной кости (кубика) возможно выпадение 1, 2, 3, 4, 5, 6 очков. Какова вероятность появления а) 6 очков, б) четного числа очков, в) 7 очков?

Задача 4. Брасают два игральных кубика. Что вероятнее - получить на верхних гранях в сумме 7 или 8 очков?

Задача 5. Предположим, что кубик бросается 2 раза. Какова вероятность, что оба раза выпадет четное количество очков (событие С)?

Задача 6. Подбрасываются три игральных кубика. Найти вероятность того, что на всех 3 кубиках выпадет четное количество очков.

Отметим, что задачи подобного содержания рассматриваются также при изучении темы «Повторные независимые испытания. Формулы Бернулли, Пуассона, Лапласа». Этот возврат к уже знакомому и понятному содержанию для студентов гуманитарных специальностей (у них хорошая память) будет способствовать более быстрому пониманию сути задачи и продемонстрирует не только связь учебных тем и понятий, но и покажет независимость полученного ответа в задаче по теории вероятностей от метода решения.

В работе рассматриваются связи математики с лингвистикой на примерах задач с множествами букв различных языков, со статистикой – на составление частотной таблицы букв определенного алфавита, со статистикой населения – пример нахождения вероятности двух мальчиков в семье из двух детей и др.

Эти примеры задач имеют для студентов-филологов также профессиональное значение, и тем самым, реализуют внутрипредметные и межпредметные связи курса, нацеливая внимание студентов на такие задачи и методы их решения, которые могут пригодиться в будущей профессиональной деятельности, реализуют также принцип наглядности и преемственности в обучении.

Одним из эффективных средств интенсификации обучения математике студентов-гуманитариев являются учебные проекты. Выполнение их способствует не только повышению интереса студентов к математике, но и формированию навыков самообразования, исследовательских и профессионально-значимых умений, а также самостоятельному приобретению математических знаний, выходящих за рамки учебного курса.

В работе исследована возможность интенсификации обучения студентов-филологов при изучении темы «Вероятностные методы изучения языков» посредством содержания профессионально-ориентированного характера, который позволяет наряду с этим закреплять основные понятия статистики. Студенты составляют таблицу частот букв иностранного языка, причем подсчет букв в тексте можно автоматизировать и построить полигон частот в MS Excel. Поясняется, как эти таблицы могут быть использованы в дешифровке текстов.

Тем самым для студентов гуманитарных специальностей дается возможность увидеть и понять применимость математических и компьютерных методов для решения профессиональных задач. Для студентов юридического факультета эта задача также вызывает интерес, поскольку принципы шифровки и дешифровки довольно часто используются в криминалистике. Это нацеливает их на понимание важности и нужности изучения математики для их будущей профессиональной деятельности, что необходимо для формирования устойчивого положительного мотива к обучению. Это же продемонстрируем и на такой задаче.

Задача 7. Городская статистика раскрываемости преступлений утверждает, что раскрывается примерно 4 на каждые 10 преступлений. Отдел внутренних дел (ОВД) одного из районов утверждает, что за последний месяц раскрыло 49 преступлений из 100. Случайны ли результаты они свидетельствуют о высоком профессионализме его работников? Принять уровень значимости равным 0,05.

Решение этой задачи заключается в проверке студентами статистической гипотезы о равенстве 0,4 вероятности раскрытия преступления районным ОВД, принятие которой означает случайный характер полученного результата 0,49. Приведенные расчеты и сравнения показывают, что с доверительной вероятностью 95% принимаем альтернативную гипотезу о том, что повышенная раскрываемость преступлений районным случайна, что говорит о высоком профессионализме его работников.

В процессе решения подобных задач у студентов формируются умения правильно выбирать необходимый математический аппарат (для этой задачи – статистический критерий), провести решение и сделать вывод по полученным результатам. Такая деятельность способствует развитию логической и стохастической составляющих мышления и повышению интереса к предмету.

Используя накопленные знания, в дальнейшем при обучении можно опускать часть, ставших уже очевидными, интуитивно понятными для студентов, действий и рассуждений, сокращая учебное время, без потери качества знаний студентов, что способствует интенсификации их обучения математике.

К условиям интенсификации относится условие преемственности обучения посредством построения и подбора задач, примеров, иллюстраций, осуществляющих подготовку студентов к восприятию нового, а в некоторых ситуациях и к самостоятельному овладению новыми знаниями. В разделе «Основы теории вероятностей» для гуманитарных специальностей примером таких задач служат задачи на изучение понятий: испытание, событие, вероятность события. Показано, что посредством таких примеров осуществляется пропедевтика новых более сложных понятий «сумма событий», «произведение событий».

Важным условием интенсификации является дифференцированный подход к обучению математике. Студенты имеют возможность выбрать посильный для себя уровень усвоения материала (основной (базовый), средний, высокий), в достижении которого главная роль отводится индивидуальным заданиям. Таким образом, практически для каждого студента можно строить обучение более интенсивно, воспитывать и развивать способности к самообразованию, т. е. получить более качественную профессиональную подготовку за отведенный срок обучения в вузе.

В исследовании обосновывается возможность строить дифференцированно обучение как на практических занятиях, так и на лекционных. Для этого сначала диагностируются знания студентов гуманитарных специальностей (входным тестированием) и в зависимости от результатов излагается учебный материал с разной степенью подробности и детальности.

Систематическое использование в курсе математики тестирования позволяет получать динамичные срезы знаний студентов и по их результатам адаптировать изложение учебного материала, делая его при необходимости более понятным и доступным, что способствует интенсификации обучения математике.

В диссертации описана методика проведения лекционной работы (с использованием активных форм: лекция-диалог, презентация), семинарских и лабораторных занятий, примеры интенсификации контроля знаний по математике (тестовые работы), основанные на выдвинутых положениях. Изложены требования к проведению различных форм занятий по математике для студентов специальностей «филология» и «юриспруденция»:

· общие: научность, доступность, единство формы и содержания, органическая связь с другими видами учебных занятий;

· специфические: для интенсификации обучения занятие должно

- иметь «напряженные» цели, четкую структуру;

- отвечать принципам наглядности, «разумной строгости», многоуровневого обучения;

- включать примеры и учебные ситуации, реализующие одновременно несколько условий интенсификации обучения математике, выделенных для студентов гуманитарных специальностей;

- иметь проблемный характер, стимулировать активную познавательную деятельность обучаемых, способствовать формированию творческого мышления;

- использовать примеры прикладного содержания по специальности для формирования положительной мотивации студентов к обучению математике;

- включать интенсивный контроль знаний студентов на занятиях.

Особое внимание в исследовании уделено самостоятельной работе студентов, на которую отводится более половины учебного времени. Разработаны лабораторных работы по математике и методика их выполнения с помощью программных продуктов (MS Excel, Advanced Grapher), при этом целесообразно объединять студентов в малые группы. В этих группах происходит взаимообучение студентов, что сокращает время изучения учебного материала. При собеседовании (защите работ) педагог может определить степень самостоятельности работы студентов и качество их знаний по математике.

Диссертационная работа содержит описание организации, содержания и основных результатов педагогического эксперимента, проведенного с целью подтверждения основной гипотезы. Педагогический эксперимент состоял из трех этапов: констатирующего (), поискового () и обучающего ( гг.). За период экспериментального обучения (один семестр) студенты имели возможность пройти от первого до третьего по сложности уровня освоения материала.

Эффективность разработанной методики подтверждается достижениями студентов и проверялась по следующим показателям: уровень математической подготовки (уровень усвоения учебного математического материала) и уровень мотивации студентов к изучению математики.

Формой итоговой отчетности по курсу математики является тестирование, анализ его результатов показал, что средний балл у студентов экспериментальной группы выше, чем в контрольной. Результаты текущего контроля показали, что более высокий уровень знаний наблюдается в экспериментальной группе, задания для которой имели профессионально-прикладной характер, и были дифференцированы по сложности.

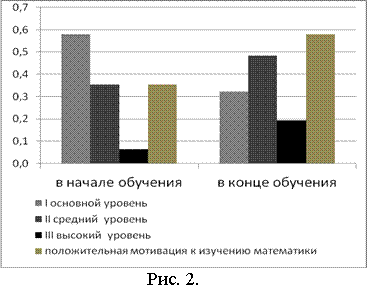
На рисунке 2 представлена динамика уровня математической подготовки студентов экспериментальной группы и уровня положительной мотивации их к изучению математики. Для проверки значимости тенденции к повышению уровня математической подготовки студентов использован t-критерий Стьюдента. Его применение показало, что с доверительной вероятностью 95% заключаем, что можно принять гипотезу о наличии такой тенденции. Проведенный формирующий эксперимент, анализ его результатов позволяют сделать вывод, что использование методической системы обучения математике студентов гуманитарных специальностей вузов в контексте интенсификации обучения способствует повышению качества знаний студентов по математике. Таким образом, подтверждена гипотеза диссертационного исследования.

В заключении диссертации подводятся итоги исследования, перечисляются основные выводы и результаты.

Анализ психолого-педагогической и научно-методической литературы, посвященной проблеме обучения математике в вузе показал, что обучение математике в контексте интенсификации представляет собой одно из перспективных направлений совершенствования математической подготовки студентов гуманитарных специальностей в высшей школе.

Специфическими чертами вузовского курса математики для студентов специальностей «юриспруденция» и «филология» являются:

- широкий спектр учебных тем и малый объем учебного аудиторного времени;

- направленность курса на общекультурное развитие студентов и их будущую профессиональную деятельность.

Разработана методическая система обучения математике студентов гуманитарных специальностей вузов в контексте интенсификации обучения, включающая цели, содержание, методы и средства обучения математике, организационные формы проведения занятий, реализующая условия интенсификации обучения.

Методической системой обучения математике студентов гуманитарных специальностей вузов в контексте интенсификации обучения предполагается:

– реализация межпредметных и внутрипредметных связей курса;

– использования оптимальных сочетаний условий интенсификации обучения математике студентов гуманитарных специальностей, ориентированные на их индивидуально-психологические особенности;

– использование системы дифференцированных заданий с включением профессионально-прикладного содержания и алгоритмов решения, индивидуальных и групповых творческих заданий;

– применение регулярного и интенсивного контроля знаний и самостоятельной работы студентов с использованием информационных технологий.

К основным профессионально важным для юриста и филолога разделам курса («Множества», «Основы теории вероятностей и математической статистики») разработана система заданий, дифференцированных по трем уровням сложности, с включением профессионально значимого содержания.

Разработаны требования и рекомендации к организации и проведению лекционных, практических занятий, лабораторных работ по математике, осуществлению контроля знаний и самостоятельной работы студентов, направленные на интенсификацию обучения. На основании выдвинутых положений диссертантом в соавторстве разработаны методические пособия «Элементы теории вероятностей», «Основы математической статистики», практикумы «Математика», «Элементы дискретной математики».

Разработана технология проведения мониторинга процесса обучения математике по следующим показателям: уровень мотивации к изучению математики, соционический тип личности, уровень математической подготовки студентов.

Проведенная опытно-экспериментальная работа показала, что разработанная методика способствует улучшению качества обучения математике студентов гуманитарных специальностей: повышается уровень усвоения учебного материала и уровень мотивации изучения математики.

Таким образом, решены все поставленные задачи исследования, цель исследования достигнута.

Основные результаты исследования отражены в следующих публикациях:

I. Публикации в журналах, рекомендованных ВАК

1. Дмитриева, М. Н. О методиках интенсификации самостоятельной работы и контроля знаний студентов гуманитарных специальностей при обучении математике и информатике / М. Н. Дмитриева // Вестник Тамбовского университета. Серия «Гуманитарные науки». – 2009. – Вып. 2(70). – С. 225 – 229.

2. Дмитриева, М. Н. Интенсификация лекционной работы и практических занятий по математике на гуманитарных факультетах вузов / М. Н. Дмитриева // Вестник Московского университета. Серия «Педагогическое образование». – 2009. – №4. – С. 97 – 104.

3. Дмитриева, М. Н. Методическая система интенсификации обучения математике студентов гуманитарных специальностей вузов / // Вестник Поморского университета. Серия «Гуманитарные и социальные науки». – 2009. – №6. – С. 146 – 149.

II. Публикации в других изданиях

4. Кондрашова (Дмитриева), компьютерных технологий при дифференцированном обучении математическим дисциплинам в вузах / М. Н. Кондрашова, Н. В. Дорошина // Сб. всерос. конф. «Математика и общество. Математическое образование на рубеже веков», Дубна. – М.: МЦНМО, 2000. – С. 396 – 397.

5. Дмитриева, М. Н. Организация контроля знаний при интенсификации обучения математике и информатике студентов-гуманитариев / // Актуальные проблемы математики и методики ее преподавания: межвуз. сб. науч. трудов, посвященный 65-летию Заслуженного деятеля науки РФ, доктора ф.-м. н., профессора . – Пенза: Изд-во Пензенского гос. пед. ун-та, 2001. – С. 256 – 261.

6. Дмитриева, М. Н. Об интенсификации курса «математика и информатика» для студентов-гуманитариев / // Секции «Методика и педагогика, проблемы высшего и среднего образования в XXI веке». Труды XXXVII всерос. науч. конф. по проблемам математики, информатики, физики, химии и методики преподавания естественнонаучных дисциплин. Москва. - М.: Изд-во ПАИМС, 2001. – С. 35 – 40.

7. Дмитриева, мотивации при интенсивном обучении математике студентов-гуманитариев / // Личность в современных исследованиях: Материалы межрегион. науч.-практ. конф. «Проблемы развития личности», Рязань, 30 окт. 2001 г.: Вып. 4 / Ряз. обл. ин-т разв. обр.; Ряз. гос. мед. ун-т. – Рязань – Москва – Ярославль. – С. 63 – 64.

8. Дмитриева, прикладной направленности курса математики и информатики для студентов гуманитарных специальностей вузов / М. Н. Дмитриева // Актуальные проблемы обучения математике (К 150-летию со дня рождения ). Т.2: Материалы всерос. науч.-практ. конф. Орел: Изд-во ОГУ, 2002. – С. 327 – 332.

9. Дмитриева, профессиональных и личностных качеств студентов-гуманитариев при интенсивном обучении их математике и информатике / // Личность в современных исследованиях. Сб. науч. трудов. Вып. 10. Материалы VII межрегион. науч.-практ. конф. «Проблемы развития личности». Рязань: Принт». – 2007. – С. 195 – 196.

10. Дмитриева, деятельности студентов гуманитарных специальностей вузов при обучении их математике / , Н. В. Дорошина // сб. статей междунар. науч. конф. «Образование, наука и экономика в вузах. Интеграция в международное образовательное пространство», 9-14 сентября 2008, г. Плоцк, Польша. – 2008. – С. 112 – 120.

11. Дмитриева, М. Н. Использование различных средств наглядности при обучении студентов математике и информатике / // Материалы VIII междунар. науч.-практ. конф. «Проблемы развития личности: психологическое консультирование и психотерапия». Вып.ноября 2008 года. Рязань, 2008. – С.174 – 176.

12. Дмитриева, математической культуры студентов гуманитарных специальностей вузов / , // Проблемы совершенствования математической подготовки в школе и ВУЗе: сб. статей. Вып. 14. – М.: МПГУ, 2009. – С. 177 – 178.

13. Дмитриева, методической системы интенсификации обучения математике студентов гуманитарных специальностей вузов / М. Н. Дмитриева // Математика в образовании: сб. статей. Вып. 6 / под ред. . – Чебоксары: Изд-во Чуваш. ун-та, 2010. – С.87 – 94.

14. Дмитриева, профессиональных и личностных качеств студентов-гуманитариев при интенсивном обучении их математике и информатике / // Материалы XI междунар. науч.-практ. конф. «Психология и медицина: пути поиска оптимального взаимодействия». – Рязань, РязГМУ, 2011. – С. 373 – 677.

Учебные пособия и практикумы

15. Кондрашова (Дмитриева), теории вероятностей: Методические указания к практическим занятиям. / Сост. М. П. Булаев, Н. В. Дорошина, М. Н. Кондрашова. Под ред. М. П. Булаева, Рязань, Ряз. гос. мед. ун-т, 2000. – 48 с. (авторский вклад – 30%).

16. Дмитриева, математической статистики: Учебное пособие / Под ред. . – Рязань, Ряз. гос. мед. ун-т, 2000. – 121 с. (авторский вклад – 30%).

17. Дмитриева, : теория вероятностей и математическая статистика / , , / Учебное пособие. Под ред. . – Рязань, РГМУ, 2002. – 205 с. (Авторский вклад – 30%).

18. Dmitrieva M. N. Mathematics: Practical Handbook /Authers-compilers M. P. Bulaev [and others]; edited by M. P. Bulaev; Ryazan State Academician I. P. Pavlov University. - Rayzan: REI RSMU, 2007. – 117 pp. (авторский вклад – 30%).

19. Дмитриева, М. Н. Математика: Практикум. / Авт.-сост. М. П. Булаев [и др.]; под. ред. М. П. Булаева. – Ряз. гос. мед. ун-т им. акад. И. П. Павлова. - Рязань: РИО РГМУ, 2007. – 124 с. (авторский вклад – 30%).

20. Дмитриева, : Практикум. / Авт.-сост. М. П. Булаев [и др.]; под. ред. М. П. Булаева. – 2-е изд., перераб. и доп. – Ряз. гос. мед. ун-т им. акад. И. П. Павлова. – Рязань: РИО РязГМУ, 2009. – 220 с. (авторский вклад – 30%).

21. Дмитриева, М. Н. Элементы дискретной математики: практикум / сост.: М. П. Булаев [и др.]; ГОУ ВПО РязГМУ Росздрава. – Рязань: РИО РязГМУ, 2010. – 100 с. (авторский вклад – 30%).