В соответствии с формулой (1.3) имеем:
![]()
Результаты обработки полученных данных по формулам (1.4) и (1.5) сведены в таблицу (Таблица 1.4.2).
Таблица 1.4.2 Распределение действительных размеров
Интервал, мм от., до | Середина интервала, мм | Частота mi | Частость pi | Плотность распределения Yi |
21,0…21,3 | 21,15 | 2 | 0,02 | 0,07 |
21,3…21,6 | 21,45 | 1 | 0,01 | 0,03 |
21,6…21,9 | 21,75 | 9 | 0,09 | 0,30 |
21,9…22,2 | 22,05 | 16 | 0,16 | 0,53 |
22,2…22,5 | 22,35 | 30 | 0,30 | 1,00 |
22,5…22,8 | 22,65 | 19 | 0,19 | 0,63 |
22,8…23,1 | 22,95 | 10 | 0,10 | 0,33 |
23,1…23,4 | 23,25 | 9 | 0,09 | 0,30 |
23,4…23,7 | 23,55 | 3 | 0,03 | 0,10 |
23,7…24,0 | 23,85 | 1 | 0,01 | 0,03 |
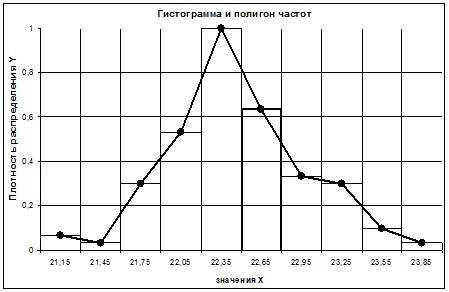
По данным из таблицы (Таблица 1.4.2) построим гистограмму и полигон частот (Рис. 1.4.1). Построение гистограммы заключается в вычерчивании смежных прямоугольников. Ширина прямоугольника гистограммы равна размеру интервала, а высота плотности распределения для данного интервала. Для построения полигона частот достаточно соединить середины прямоугольников образующих гистограмму.
Вычисления среднего значения выборки и среднеквадратического отклонения по формулам (1.6) и (1.7) дают:
αср=22,47; σ=0,5
Таблица 1.4.3 Данные для построения кривой нормального распределения
αiср | Xi= αiср–αср | ti=Xi /σ |
| Yi=Yi’/σ |
21,15 | -1,32 | -2,65 | 0,01 | 0,02 |
21,45 | -1,02 | -2,05 | 0,05 | 0,10 |
21,75 | -0,72 | -1,45 | 0,14 | 0,28 |
22,05 | -0,42 | -0,85 | 0,28 | 0,56 |
22,35 | -0,12 | -0,25 | 0,39 | 0,77 |
22,65 | 0,18 | 0,35 | 0,38 | 0,75 |
22,95 | 0,48 | 0,95 | 0,25 | 0,51 |
23,25 | 0,78 | 1,55 | 0,12 | 0,24 |
23,55 | 1,08 | 2,15 | 0,04 | 0,08 |
23,85 | 1,38 | 2,75 | 0,01 | 0,02 |
Рис. 1.4.1 Пример построения гистограммы и полигона частот.
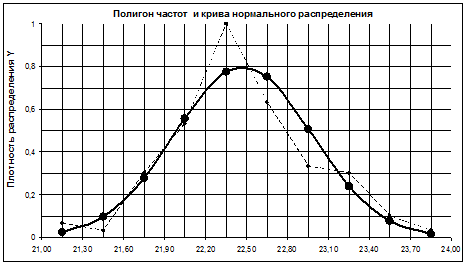
Рис. 1.4.2. Пример построения кривой распределения случайной величины с использованием полигона частот.
Содержание отчета.
Наименование работы. Наименование станка, модель. Эскизы механической обработки детали (кольцо) и измерение размера партии деталей. Данные измерительного микрометра: наименование, цена деления. Данные режущего инструмента. Результаты измерений. Расчет величин αср и σ по формулам (1.6) и (1.7). Построение эмпирической кривой распределения действительных размеров. Построение кривой нормального распределения. Сравнение эмпирической кривой распределения с нормальной. Анализ результатов и выводы.Контрольные вопросы.
Чем отличается дискретная случайная величина от непрерывной? Записать уравнение закона нормального распределения. Что такое среднеарифметическое значение, и каким образом его определяют? Как определяется среднее квадратичное отклонение σ? Как влияет значение σ на распределение случайной величины? Как определить максимальную ординату кривой Гаусса? Какова величина теоретического поля рассеивания значений случайной величины?Лабораторная работа №2
"Определение процента возможного брака по площади кривой распределения".
Цель работы:
Изучение параметров и математических зависимостей, характеризующих закон нормального распределения. Анализ точности исследуемой операции: с помощью закона нормального распределения.
Основные теоретические положения.
Эмпирические кривые распределения действительных размеров имеют вид ломаной линии, поэтому вывести какие-либо общие закономерности на основании их рассмотрения трудно. Для получения более достоверных закономерностей распределения необходимо увеличить количество деталей, измеренных с точностью, разрешающей значительно увеличить число интервалов. В таком случае эмпирическая кривая будет приближаться к форме плавной кривой нормального распределения. На практике для сопоставления и определения степени приближения кривых распределения обе кривые вычерчиваются на графике в одинаковом масштабе.
Для заданного распределения находят среднее арифметическое значение действительных размеров αср и среднее квадратичное отклонение σ.Среднее арифметическое значение действительных размеров деталей αср определит положение кривой нормального распределения, так как это есть центр группирования. Зная среднеквадратическое отклонение, σ вычисляют параметры кривой нормального распределения по формуле (1.1).
По полученным данным, используя результаты лабораторной работы №1, строят кривую нормального распределения непосредственно на графике рассеивания размеров. Затем на этот график наносят в принятом масштабе величину заданного поля допуска с предельными размерами и через нижнюю и верхнюю границы допуска проводят ординаты до пересечения с кривой нормального распределения. Полагая, что рассеивание фактических размеров соответствует нормальному закону распределения, можно определить вероятность соблюдения заданного допуска обработки по исследуемой операции. Часть площади под кривой между проведенными ординатами соответствует количеству деталей, размеры которых не выходят за пределы поля допуска. Вероятность получения деталей в пределах поля допуска равняется отношению площади, заключенной между кривой распределения и ординатами, проведенными через концы поля допуска ко всей площади кривой распределения.
Для определения количества годных заготовок необходимо найти площадь, ограниченную кривой и осью абсцисс на длине, равной допуску
T=Lmax–Lmin. При симметричном расположении поля допуска (Рис. 2.2.1) следует определить значение интеграла, определяющего площадь, ограниченную кривой Гаусса и абсциссой x0
(2.1) |
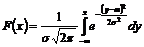
Интеграл (2.1) не может быть выражен через элементарные функции.
Воспользовавшись интегральной функцией Лапласа
(2.2) |
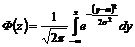
Выражение можно привести к виду
(2.3) |
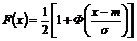
Интегральная функция Лапласа нечетная:
(2.4) |
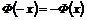
На основании формул (2.3) – (2.4) площадь, ограниченная кривой нормального распределения на интервале (a, b):
(2.5) |
![]()
Значение функции Лапласа Ф(t) можно определить по таблице 2.2.1, а можно вычислить по эмпирической формуле:
(2.6) |
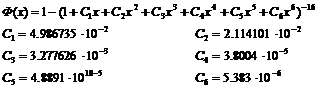
Введем новое понятие – коэффициент риска. Коэффициент риска t определяется выражением
(2.7) |
![]()
Где x –значение величины размера;
m и σ –математическое ожидание и среднеквадратическое отклонение соответственно.
Вместо среднеквадратического отклонения, в случае эмпирического распределения, необходимо использовать другую величину исправленное среднее s.
Величина исправленного среднего отклонения определяется по формуле:
![]()
Где n –количество испытаний.
После этого коэффициент риска определится как:
![]()
Тогда (2.5) примет вид:
(2.8) |
![]()
Расчет количества годных заготовок сводится к установлению величины t и определению по таблице (Таблица 2.2.1)значении функции Ф(t), с последующим пересчетом полученных величин в проценты или в число штук заготовок.
Например: партия заготовок n=300 шт. параметры закона распределения:
m=35,26
σ=0,4
Δ=35,2±0,5
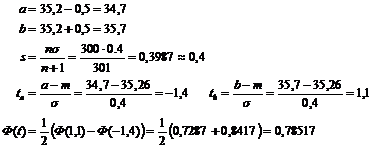
Получили Ф(t)=0,785 что соответствует 78,5% от всей партии или 235,5~236 шт., а бракованных – 21,5% или 64 шт.
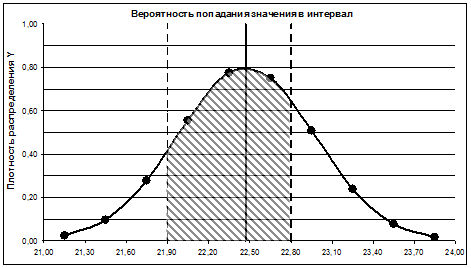
Рис. 2.2.1. Определение вероятности попадания значения случайной величины в заданный интервал.
Таблица 2.2.1 Значения функции Лапласа Ф(t)
t | Ф(t) | t | Ф(t) | t | Ф(t) | t | Ф(t) | t | Ф(t) | t | Ф(t) |
0,00 | 0,0000 | 0,5 | 0,3829 | 1 | 0,6827 | 1,5 | 0,8664 | 2 | 0,9545 | 2,5 | 0,9876 |
0,01 | 0,0080 | 0,51 | 0,3899 | 1,01 | 0,6875 | 1,51 | 0,8690 | 2,01 | 0,9556 | 2,51 | 0,9879 |
0,02 | 0,0160 | 0,52 | 0,3969 | 1,02 | 0,6923 | 1,52 | 0,8715 | 2,02 | 0,9566 | 2,52 | 0,9883 |
0,03 | 0,0239 | 0,53 | 0,4039 | 1,03 | 0,6970 | 1,53 | 0,8740 | 2,03 | 0,9576 | 2,53 | 0,9886 |
0,04 | 0,0319 | 0,54 | 0,4108 | 1,04 | 0,7017 | 1,54 | 0,8764 | 2,04 | 0,9586 | 2,54 | 0,9889 |
0,05 | 0,0399 | 0,55 | 0,4177 | 1,05 | 0,7063 | 1,55 | 0,8789 | 2,05 | 0,9596 | 2,55 | 0,9892 |
0,06 | 0,0478 | 0,56 | 0,4245 | 1,06 | 0,7109 | 1,56 | 0,8812 | 2,06 | 0,9606 | 2,56 | 0,9895 |
0,07 | 0,0558 | 0,57 | 0,4313 | 1,07 | 0,7154 | 1,57 | 0,8836 | 2,07 | 0,9615 | 2,57 | 0,9898 |
0,08 | 0,0638 | 0,58 | 0,4381 | 1,08 | 0,7199 | 1,58 | 0,8859 | 2,08 | 0,9625 | 2,58 | 0,9901 |
0,09 | 0,0717 | 0,59 | 0,4448 | 1,09 | 0,7243 | 1,59 | 0,8882 | 2,09 | 0,9634 | 2,59 | 0,9904 |
0,10 | 0,0797 | 0,6 | 0,4515 | 1,1 | 0,7287 | 1,6 | 0,8904 | 2,1 | 0,9643 | 2,6 | 0,9907 |
0,11 | 0,0876 | 0,61 | 0,4581 | 1,11 | 0,7330 | 1,61 | 0,8926 | 2,11 | 0,9651 | 2,61 | 0,9909 |
0,12 | 0,0955 | 0,62 | 0,4647 | 1,12 | 0,7373 | 1,62 | 0,8948 | 2,12 | 0,9660 | 2,62 | 0,9912 |
0,13 | 0,1034 | 0,63 | 0,4713 | 1,13 | 0,7415 | 1,63 | 0,8969 | 2,13 | 0,9668 | 2,63 | 0,9915 |
0,14 | 0,1113 | 0,64 | 0,4778 | 1,14 | 0,7457 | 1,64 | 0,8990 | 2,14 | 0,9676 | 2,64 | 0,9917 |
0,15 | 0,1192 | 0,65 | 0,4843 | 1,15 | 0,7499 | 1,65 | 0,9011 | 2,15 | 0,9684 | 2,65 | 0,9920 |
0,16 | 0,1271 | 0,66 | 0,4907 | 1,16 | 0,7540 | 1,66 | 0,9031 | 2,16 | 0,9692 | 2,66 | 0,9922 |
0,17 | 0,1350 | 0,67 | 0,4971 | 1,17 | 0,7580 | 1,67 | 0,9051 | 2,17 | 0,9700 | 2,67 | 0,9924 |
0,18 | 0,1428 | 0,68 | 0,5035 | 1,18 | 0,7620 | 1,68 | 0,9070 | 2,18 | 0,9707 | 2,68 | 0,9926 |
0,19 | 0,1507 | 0,69 | 0,5098 | 1,19 | 0,7660 | 1,69 | 0,9090 | 2,19 | 0,9715 | 2,69 | 0,9929 |
0,2 | 0,1585 | 0,7 | 0,5161 | 1,2 | 0,7699 | 1,7 | 0,9109 | 2,2 | 0,9722 | 2,7 | 0,9931 |
0,21 | 0,1663 | 0,71 | 0,5223 | 1,21 | 0,7737 | 1,71 | 0,9127 | 2,21 | 0,9729 | 2,71 | 0,9933 |
0,22 | 0,1741 | 0,72 | 0,5285 | 1,22 | 0,7775 | 1,72 | 0,9146 | 2,22 | 0,9736 | 2,72 | 0,9935 |
0,23 | 0,1819 | 0,73 | 0,5346 | 1,23 | 0,7813 | 1,73 | 0,9164 | 2,23 | 0,9743 | 2,73 | 0,9937 |
0,24 | 0,1897 | 0,74 | 0,5407 | 1,24 | 0,7850 | 1,74 | 0,9181 | 2,24 | 0,9749 | 2,74 | 0,9939 |
0,25 | 0,1974 | 0,75 | 0,5467 | 1,25 | 0,7887 | 1,75 | 0,9199 | 2,25 | 0,9756 | 2,75 | 0,9940 |
0,26 | 0,2051 | 0,76 | 0,5527 | 1,26 | 0,7923 | 1,76 | 0,9216 | 2,26 | 0,9762 | 2,76 | 0,9942 |
0,27 | 0,2128 | 0,77 | 0,5587 | 1,27 | 0,7959 | 1,77 | 0,9233 | 2,27 | 0,9768 | 2,77 | 0,9944 |
0,28 | 0,2205 | 0,78 | 0,5646 | 1,28 | 0,7995 | 1,78 | 0,9249 | 2,28 | 0,9774 | 2,78 | 0,9946 |
0,29 | 0,2282 | 0,79 | 0,5705 | 1,29 | 0,8029 | 1,79 | 0,9265 | 2,29 | 0,9780 | 2,79 | 0,9947 |
0,30 | 0,2358 | 0,8 | 0,5763 | 1,3 | 0,8064 | 1,8 | 0,9281 | 2,3 | 0,9786 | 2,8 | 0,9949 |
0,31 | 0,2434 | 0,81 | 0,5821 | 1,31 | 0,8098 | 1,81 | 0,9297 | 2,31 | 0,9791 | 2,81 | 0,9950 |
0,32 | 0,2510 | 0,82 | 0,5878 | 1,32 | 0,8132 | 1,82 | 0,9312 | 2,32 | 0,9797 | 2,82 | 0,9952 |
0,33 | 0,2586 | 0,83 | 0,5935 | 1,33 | 0,8165 | 1,83 | 0,9327 | 2,33 | 0,9802 | 2,83 | 0,9953 |
0,34 | 0,2661 | 0,84 | 0,5991 | 1,34 | 0,8198 | 1,84 | 0,9342 | 2,34 | 0,9807 | 2,84 | 0,9955 |
0,35 | 0,2737 | 0,85 | 0,6047 | 1,35 | 0,8230 | 1,85 | 0,9357 | 2,35 | 0,9812 | 2,85 | 0,9956 |
0,36 | 0,2812 | 0,86 | 0,6102 | 1,36 | 0,8262 | 1,86 | 0,9371 | 2,36 | 0,9817 | 2,86 | 0,9958 |
0,37 | 0,2886 | 0,87 | 0,6157 | 1,37 | 0,8293 | 1,87 | 0,9385 | 2,37 | 0,9822 | 2,87 | 0,9959 |
0,38 | 0,2961 | 0,88 | 0,6211 | 1,38 | 0,8324 | 1,88 | 0,9399 | 2,38 | 0,9827 | 2,88 | 0,9960 |
0,39 | 0,3035 | 0,89 | 0,6265 | 1,39 | 0,8355 | 1,89 | 0,9412 | 2,39 | 0,9832 | 2,89 | 0,9961 |
0,40 | 0,3108 | 0,9 | 0,6319 | 1,4 | 0,8385 | 1,9 | 0,9426 | 2,4 | 0,9836 | 2,9 | 0,9963 |
0,41 | 0,3182 | 0,91 | 0,6372 | 1,41 | 0,8415 | 1,91 | 0,9439 | 2,41 | 0,9840 | 2,91 | 0,9964 |
0,42 | 0,3255 | 0,92 | 0,6424 | 1,42 | 0,8444 | 1,92 | 0,9451 | 2,42 | 0,9845 | 2,92 | 0,9965 |
0,43 | 0,3328 | 0,93 | 0,6476 | 1,43 | 0,8473 | 1,93 | 0,9464 | 2,43 | 0,9849 | 2,93 | 0,9966 |
0,44 | 0,3401 | 0,94 | 0,6528 | 1,44 | 0,8501 | 1,94 | 0,9476 | 2,44 | 0,9853 | 2,94 | 0,9967 |
0,45 | 0,3473 | 0,95 | 0,6579 | 1,45 | 0,8529 | 1,95 | 0,9488 | 2,45 | 0,9857 | 2,95 | 0,9968 |
0,46 | 0,3545 | 0,96 | 0,6629 | 1,46 | 0,8557 | 1,96 | 0,9500 | 2,46 | 0,9861 | 2,96 | 0,9969 |
0,47 | 0,3616 | 0,97 | 0,6680 | 1,47 | 0,8584 | 1,97 | 0,9512 | 2,47 | 0,9865 | 2,97 | 0,9970 |
0,48 | 0,3688 | 0,98 | 0,6729 | 1,48 | 0,8611 | 1,98 | 0,9523 | 2,48 | 0,9869 | 2,98 | 0,9971 |
0,49 | 0,3759 | 0,99 | 0,6778 | 1,49 | 0,8638 | 1,99 | 0,9534 | 2,49 | 0,9872 | 2,99 | 0,9972 |
Порядок проведения работы.
Для выполнения лабораторной работы 2 используем результаты работы 1, т. е. известны значения, YMAX, ,Y, , Td.
1. Определяем значение ![]() , где n –количество измерений, шт. ,σ - среднеквадратическое отклонение, полученное по формуле (1.7) в результате измерения действительных размеров.
, где n –количество измерений, шт. ,σ - среднеквадратическое отклонение, полученное по формуле (1.7) в результате измерения действительных размеров.
2. Используя таблицу функции Лапласа по известному значению определяем Ф(t)
3. Определяем количество годных и бракованных деталей в партии.
Содержание отчета.
1. Наименование работы.
2. Наименование станка: модель, характеристика.
3. Эскизы механической обработки и измерение размера партии деталей.
4. Данные измерительного и режущего инструментов.
5. По известной кривой распределения действительных размеров определить процент годных деталей.
6. Расчет величин t и (t)
7. Анализ результатов и выводы.
Контрольные вопросы
1. Что представляет собой коэффициент риска t?
2. Как влияет значение t на количество годных заготовок?
3. Как определяется расчетное значение, если известное значение среднеквадратичного отклонения по результатам замеров?
4. Как определяется количество годных и бракованных заготовок в процентах и штуках, если известно значение функции Ф(t).
Лабораторная работа №3
"Статистические методы исследования точности при фрезеровании".
Цель работы:
Исследование влияния случайных погрешностей на точность обработки.
Основные теоретические положения.
При анализе точности технологического процесса приходится рассматривать как систематические, так и случайные погрешности обработки. Систематической называется такая погрешность, которая в рамках рассматриваемой задачи остается постоянной или же изменяется закономерно. Случайной называется такая погрешность, которая в рамках рассматриваемой задачи имеет различные значения, причем определить заранее точное ее значение для каждого момента не представляется возможным.
Случайные погрешности вызываются действием на процесс целого ряда независимых друг от друга случайных факторов. Например, диаметр отверстия при растачивании будет у разных деталей различным, что вызывается неодинаковыми припусками, неодинаковой твердостью обрабатываемого материала, погрешностями измерения и т. п. Влияние случайных факторов выражается в рассеивании размеров, исследование случайных погрешностей основывается на выводах теории вероятности и математической статистики. При изучении случайных погрешностей удобно пользоваться кривыми распределения. Кривые распределения строятся на основании многократных наблюдений одного и того же явления.
В данной работе в качестве такого явления будет служить получение размера “h” на валике (рисунок 1.3) путем фрезерования на предварительно настроенном фрезерном станке.
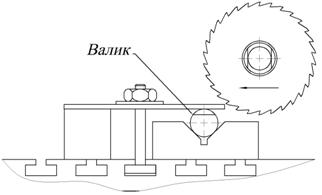
Рис. 3.2.1 Схема фрезерования валика.
Порядок проведения работы.
Установить фрезу 1 относительно приспособления 3 на установочный размер h.
В приспособлении 3 установить обрабатываемый валик.
Не нарушая установочной базы обработать лыску на валике.
Повторить пункт 3 на партиях деталей в количестве 30 – 50 шт.
Измерить величину размера h на каждом валике и свести в таблицу. Для измерения размера h использовать микрометр.
Далее выполнить действия и расчеты, указанные в методических указаниях к лабораторной работе 1.
Содержание отчета
1. Наименование работы.
2. Наименование станка: модель, характеристика.
3. Эскизы механической обработки валика и измерение размера обработки партии деталей.
4. Данные измерительного микрометра: наименование, цена деления.
5. Данные режущего инструмента – фрезы.
6. Результаты измерений свести в таблицу 1.3.
7. Построение опытной кривой распределения действительных размеров h.
8. Сравнение опытной кривой с нормальной.
9. Расчет величин hср и.
10. Анализ результатов и выводов.
Контрольные вопросы.
1. Какой параметр закона Гаусса характеризует положение центра группирования?
2. Какие погрешности обработки возникают в процессе формирования?
3. Повторить контрольные вопросы по лабораторной работе 1?
Список использованных источников:
1. и др. Лабораторные работы по технологии машиностроения. Л.: Машиностроение , 19с. (с.13-16)
2. Маталин машиностроения. Л.: Машиностроение, 19с. (c.63-74).
3. Шелест в физике.—М.: Наука. Гл. ред. физ.-мат. лит., 1988.—272 с.
4. руководство к решению задач по теории вероятности и математической статистике. Изд. 2-е, доп. М., «Высш. Школа», 1975.—333с. с ил.
Составители: Ярослав Николаевич Отений,
Николай Иванович Никифоров
СТАТИСТИЧЕСКИЕ МЕТОДЫ
ИССЛЕДОВАНИЯ ТОЧНОСТИ
МЕХАНИЧЕСКОЙ ОБРАБОТКИ
методические указания
к лабораторным работам
Издано в редакции авторов
Темплан 2004 г., поз. № 000.
№ 000 от 01.01.2001
Подписано в печать г.
Формат стандартный 60×84 1/16. Бумага потребительская.
Усл. печ. л. 1,5. Уч. – изд. л1,31
Тираж 100 экз. Заказ
Волгоградский государственный технический университет.
400131 Волгоград, просп. Им. , 28.
РПК «Политехник»
Волгоградского государственного технического университета
400131 Волгоград, ул. Советская, 35.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 |