-3x + 12 = 2x + 2 + t,
t = 10 – 5x,
T = xt = x×(10 – 5x) = 10x – 5x2.
Находим максимум функции T:
T¢ = 10 – 10x = 0,
x =1,
T² = -10 < 0,
следовательно, x = 1 – точка максимума.
В точке x = 1 находим t = 5, T = 5. Следовательно, доход государства максимален при t = 5.
Задача 4
Функция общих затрат монополии имеет вид ТС = 200 + 30Q, функция спроса на ее продукцию Р = 60 – 0,2Q. Определить цену, при которой фирма максимизирует прибыль.
Решение
I = TR – TC, так как TR = Q × P,
то I = 60Q – 0,2Q2 – Q = 0,2Q + 30Q – 200,
I¢ = -0,4Q + 30,
I¢ = 0 Þ -0,4Q + 30 = 0, тогда Q = 75, значит Р = 60 – 0,2 × 75 = 45.
Задача 5
Функция суточного спроса Q на мороженое (тыс. шт.) в зависимости от цены Р за одну порцию (руб) имеет вид 
. Эффективная область «работы» этой формулы от 1 до 9 руб. При какой цене за порцию мороженого совокупная выручка будет максимальной?
Решение
Совокупная выручка определяется из соотношения TR = Q ×.P, где Q – количество реализованных порций мороженого (тыс. шт.); Р – цена за одну порцию (руб). Тогда функция совокупной выручки в зависимости от цены примет вид:
.
Требуется найти наибольшее значение этой функции на отрезке [1; 9].
Для этого находим критические точки функции, принадлежащие данному отрезку:
Критическая точка Р = 4. Вычислим значение функции совокупной выручки на концах интервала и в критической точке:
TR(1) =. 1 = 2;
TR(4) =. 4 = 4;
TR(9) = 0.
Следовательно, при цене 4 руб за порцию совокупная выручка будет максимальной и составит 4000 руб.
Задача 6
Некоторая монополия продает свою продукцию на двух рынках, функции спроса на которых 
и 
, функция издержек ТС = Q2. Найти точку (Q1 и Q2), в которой значение функции прибыли I = P1Q1 + P2Q2 – TC(Q).
Решение
Составим функцию прибыли I = P1Q1 + P2Q2 – TC(Q) для этого найдем Р1 и Р2:
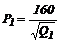и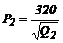 
,
значит 
,
.
Находим критические точки:
,
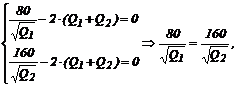
Q2 = 4Q1,
,
,
64= Q13 Þ Q1 = 4, Q2 = 16.
Следовательно Q1 = 4, Q2 = 16, I = 1200.
Задача 7
Объем продаж видеомагнитофонов задается следующей функцией времени:
V(t) = 5000 + 1000t -100t2,
где t – время, измеряемое в месяцах; V – количество видеомагнитофонов, проданных за месяц.
Найти скорость изменения объема продаж в момент времени:
а) t = 0; б) t = 2; в) t = 6.
Задача 8
Население некоторой страны растет по следующему закону:
P(t) = 100000 × (1 + t)2,
где время t измеряется в годах. Найти скорость изменения населения в момент времени:
а) t = 0; б) t = 2; в) t = 5.
Задача 9
Эпидемия медленно распространяется среди населения. Число заболевших определяется формулой:
,
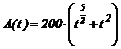где t – число недель, прошедших с момента начала эпидемии.
Найти скорость изменения числа заболевших в момент времени:
а) t = 1; б) t = 4; в) t = 9.
Задача 10
Предположим, что издержки получения питьевой воды заданы формулой:
где t – процентное содержание загрязняющих воду примесей.
Найти скорость изменения издержек производства, если примеси составляют 5 %.
Задача 11
Количество произведенной за день продукции Q(x) зависит от числа рабочих в сборочном цехе следующим образом:
Q(x) = 100х + Зх2,
где х – число рабочих.
а) Если в сборочном цехе работали 70 человек, оценить изменение
количества произведенной за неделю продукции, вызванное добавлением одного рабочего.
б) Найти точное значение прироста выработки за неделю, вызванного добавлением одного рабочего.
Задача 12
Месячное производство Q(x) некоторого продукта зависит от инвестиций следующим образом:
,
где х – инвестированный капитал в миллионах рублей.
Вычислить точно и приближенно прирост производства, вызванный дополнительным вложением 1 млн. руб, если первоначальные инвестиции
составляли 100 млн. руб.
Задача 13
Издержки производства некоторой продукции имеют вид:
С(х) = 100 + 3х + х2,
где х – число единиц продукции. Цена на этот товар составляет 20. Найти функцию предельной прибыли и ее значение в точке 30. Объяснить экономический смысл значения Р'(3О). Вычислить и объяснить смысл величины Р(31) - Р(30).
Задача 14
Издержки производства некоторой продукции имеют вид:
С(х) = 150 + 10х + 0,01х2,
где х – число единиц продукции. Цена на этот товар составляет 36. Найти функцию прибыли и функцию предельной прибыли. Объяснить экономический смысл величины Р'(15). Вычислить и объяснить смысл величины Р(16) - Р(15).
Задача 15
Функция издержек производства некоторой продукции определяется следующей формулой:
а) С(х) = 2000 + 10Ох + 0,1х2;
б) С(х) = 3500 + 150х + 0,2х2,
где х – число единиц произведенной продукции.
Найти функцию предельных издержек, средние издержки производства х единиц продукции и скорость изменения средних издержек. При каком уровне производства скорость изменения средних издержек равна нулю?
Задача 16
В гостинице 60 номеров. При цене 300 руб за номер в сутки бывает занято 50 номеров. Если цена снижается до 280 руб за номер, то занято 55 номеров. Найти максимальное значение выручки, предполагая линейным закон спроса. При какой цене достигается это значение?
Задача 17
Ресторан рассчитан не более чем на 100 посетителей. При цене 120 руб, за обед бывает 70 посетителей, а при цене 100 руб за обед число посетителей возрастает до 80. Фиксированные издержки приготовления обеда составляют 900 руб в день, а переменные – 40 руб за обед. Найти функцию прибыли, предполагая линейной зависимость между числом посетителей и ценой обеда. Каково максимальное значение прибыли?
Задача 18
Цена на некоторый товар составляет 250 руб. Издержки производства этого товара равны 120х + х2, где х – число единиц произведенного товара. Найти максимальное значение прибыли.
Задача 19
Издержки производства некоторой продукции определяются функцией 5x2 + 80x, где х – число единиц произведенной за месяц продукции. Эта продукция продается по цене 280 руб за изделие. Сколько изделий нужно произвести и продать, чтобы прибыль была максимальна.
Задача 20
Пусть известны функции соответственно спроса и предложения на некоторый товар на конкурентном рынке:
р = 2х + 50,
р = - х + 200,
где х – число единиц товара.
Предположим, что средние издержки производства одной единицы товара определяются следующей функцией:
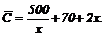
Найти максимальное значение прибыли.
Задача 21
Если собрать урожай в начале августа, то с каждой сотки можно получить 200 кг раннего картофеля и реализовать его по 12 руб за килограмм. Отсрочка уборки на каждую неделю ведет к увеличению урожайности на 50 кг с одной сотки, но цена картофеля за килограмм при этом падает на 2 руб. Когда следует собрать картофель, чтобы доход от его продажи был максимальным, если срок уборки составляет 5 недель?
Задача 22
Издержки производства некоторого товара равны ТС = 4 + 15Q; спрос на товар определяется, функцией Р = -Q2 + 20Q + 2; 10 < Q < 20.
Найти объем продукции Q, максимизирующий прибыль.
 |
Задача 23
Компания нашла покупателя, согласного покупать у нее 20000 единиц некоторого товара в год. Подготовка к производству одной партии составляет 30 руб. Производство одной единицы товара обходится в 9 руб, а издержки хранения составляют 0,3 руб за единицу товара в год. Найти число единиц товара в партии, при котором совокупные издержки производства и хранения будут минимальны.
Задача 24
Компания должна произвести 96000 единиц продукции в год. Издержки подготовки к производству одной партии составляют 1500 руб, а издержки производства одной единицы продукции – 10 руб. Хранение обходится в 0,5 руб за единицу товара в год. Найти число единиц товара в партии, при котором совокупные издержки производства и хранения будут минимальны.
Задача 25
Функция спроса имеет вид:
.
а) Найти эластичность спроса в точке р = 50.
б) Посчитать приближенно процентное изменение спроса, если цена выросла на 11 %.
Задача 26
Уравнение спроса имеет вид:
.
а) Найти эластичность спроса в точке р = 18.
б) Вычислить приближенно процентное изменение спроса, если цена уменьшилась на 2 %.
Задача 27
Уравнение спроса имеет вид:
.
Найти эластичность и выяснить, как повлияет увеличение цены на
выручку, если спрос составляет:
а) 150 единиц; б) 50 единиц
Задача 28
Уравнение спроса имеет вид:
.
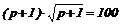Найти эластичность и выяснить, как повлияет увеличение цены на выручку, если спрос составляет:
а) 24 единицы; б) 15 единиц.
Задача 29
Функция общих затрат фирмы имеет вид ТС = 100Q - 2Q2 + 0.04Q3. Определить величину предельных затрат фирмы при Q = 12 единиц.
Задача 30
Известно, что постоянные затраты фирмы равны 55 денежных единиц. Функция предельных затрат фирмы имеет вид МС = 22 - 8Q + 3Q3. Определить функцию общих затрат фирмы и рассчитать эти затраты при выпуске 3 единиц продукции.
Задача 31
Функция средних переменных затрат имеет вид AVC = 10 + 2Q. Постоянные затраты равны 12 ден. един. Найти алгебраическое выражение для функций общих и предельных затрат.
Задача 32
Функция общих затрат предприятия имеет вид ТС = 30 + 5Q + Q2. Определить выражение для постоянных, переменных, предельных, средних, общих, средних постоянных и средних переменных затрат как функции от Q. При каком значении Q средние общие затраты достигают минимума?
Задача 33
Известно, что постоянные затраты фирмы составляют 80 денежных единиц. Функция предельных затрат имеет вид МС = 30 - 10Q + 6Q2 +1,6Q3. Определить функцию общих затрат фирмы и рассчитать эти затраты при выпуске трех единиц продукции.
Задача 34
Функция спроса населения на данный товар имеет вид Qd = 14 - 2Р, функция предложения данного товара Qs = -4 + 2Р. Определить ставку налога, при которой равновесный объем продаж составит две единицы.
Задача 35
Функция спроса населения на данный товар Qd = 10 - Р, функция предложения данного товара Qs = -5 + 2Р. Предположим, что на данный товар введен налог, уплачиваемый продавцом, в размере трех денежных единиц за штуку. Определить величину чистых потерь, обусловленных введением налога.
Задача 36
Функция спроса населения на данный товар Qd = 7 - Р, функция предложения данного товара Qs = -5 + 2Р. При какой ставке налога общая сумма налога окажется максимальной?
Задача 37
Функция спроса населения на данный товар имеет вид Qd = 8 - Р, а функция предложения данного товара Qs = -5 + 2Р. Предположим, что на данный товар введен налог, уплачиваемый продавцом, в размере одной денежной единицы. Определить: а) цену для покупателя и цену для продавца с учетом налога; б) общую сумму вносимого в бюджет налога.
Задача 38
Монополия максимизирует выручку при целевой прибыли не ниже 1500 млн. руб. Известны функция спроса на продукцию монополиста Р = 304 - 2Q и функция затрат ТС = 500 + 2Q + 8Q2. Определить оптимальный объем выпуска при данной прибыли и выпуск, при котором прибыль монополии максимальна.
Задача 39
Фирма находится в условиях совершенной конкуренции. Функция общих затрат имеет вид ТС = 0,1Q2 + 15Q + 10. Какой объем производства продукции выберет фирма, если цена товара двадцать пять денежных единиц.
Задача 40
Фирма выпускает товар и продает его по цене четырнадцать денежных единиц. Функция общих издержек фирмы ТС = 2Q + Q3. При каком объеме выпуска прибыль фирмы будет максимальна.
Задача 41
Производственная форма фирмы имеет вид: Q = K0,5 × L0,5. Предположим, что в день затрачивается 4 часа труда (L = 4) и 4 часа работы машины (K = 4). Определить:
1) максимальное количество продукции;
2) средний продукт труда;
3) допустим, что фирма увеличила затраты обоих факторов в два раза. Каков будет объем выпускаемой продукции?
Задача 42
Монополия владеет двумя предприятиями, функция затрат которых дана: ТС1 = 10Q1, ТС2 = 0,2Q22. Функция спроса на продукцию монополиста Q = 200 – 2Р. Определить оптимальную для монополиста цену.
Задача 43
Функция затрат монополии имеет вид ТС = 5Q + 0,25Q2. Монополия торгует на двух рынках, функция спроса на которых Q1 = 160 – Р1; Q2 = 160 – Р2. Определить цены на каждом рынке, при которых прибыль монополии будет максимальной.
Задача 44
Предположим, что производственная функция фирмы имеет вид: 
. Если количество применяемого труда возрастает на 8 %, а капитала на 4 %, то на сколько увеличится объем выпуска?
3. Применение интегрального исчисления
Интегрирование используется для нахождения функций издержек, прибыли, потребления, если известны соответственно функции предельных издержек, предельной прибыли и т. д. Для определения произвольной постоянной интегрирования необходимо дополнительное условие. Если находится функция издержек, используется то, что ее значение в точке х = 0 (х – число единиц произвольной продукции) равно значению фиксированных издержек, а при определении функции дохода – то, что ее значение в точке х = 0 равно нулю (доход равен нулю, если не продано ни одного изделия).
Задача 1
Задана функция предельного дохода:
R'(x) = 20 - 0,04х.
Найти функцию дохода и закон спроса на продукцию.
Решение
,
R(0) =0, следовательно, С = 0,
R(x) = 20 x - 0,02x2.
Если каждая единица продукции продается по цене р, то доход определяется формулой R = хр. Следовательно, деля на х функцию дохода, находим закон спроса р(х):
р =,02х.
Коэффициент неравномерности распределения дохода. Рассмотрим функцию у = f(x), где у – это доля совокупного дохода, получаемая частью х наиболее низко оплачиваемого населения. Например, 
означает, что 80 % наиболее низко оплачиваемого населения получают 60 % совокупного дохода. Очевидно, что 0 < х < 1, 0 < у < 1; у £ х. Предположим, что нет населения с нулевым доходом, т. е. у(0) = 0, и весь доход получается всей совокупностью населения, т. е. у(1) = 1.
На рис. 9 показан пример графика функции у = f(x). Эта кривая называется кривой Лоренца. Если бы распределение доходов было совершенным, то 10 % населения получали бы 10 % совокупного дохода, 20 % населения – 20 % дохода и т. д. Тогда кривой распределения доходов была бы прямая у = х. Отклонение реального распределения доходов от идеального измеряется отношением L площади между прямой у = х и кривой Лоренца к площади, ограниченной прямыми у = х; х = 1 и осью х, и называется коэффициентом нерав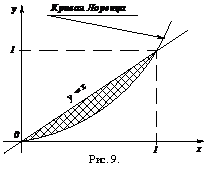
номерности распределения доходов
Очевидно, что 0 £ L £ 1. Зна-чение L = 0 соответствует совер-шенному распределению доходов.
Кривая обучения. Часто необходимо оценить, сколько вре-мени потребуется для производства некоторого дополнительного коли-чества продукции. Для подобных расчетов пользуются так назы-ваемой кривой обучения.
Пусть Т = F(x) – время, измеряемое в человеко-часах, необходимое для производства первых х единиц продукции. Тогда f(x) = F'(x) приближенно равно времени, необходимому для производства (х + 1)-й единицы продукции. Обычно используют функции вида:
где а > 0, -1 < b < 0.
График функции такого вида изображен на рис. 10 и называется кривой обучения.
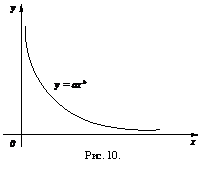Функция f(x ) – убывающая, так как время, необходимое для выполнения некоторой операции, убывает при возрастании числа повторов.
Время ΔT, необходимое для производства единиц продукции с номерами от п1 до п2, определяется формулой:
.
Задача 2
После сборки 100 часов оказалось, что в дальнейшем время убывает в соответствии с формулой у = 15х -0,14. Найти время, которое потребуется для сборки еще 20 часов (т. е. с номера 101 до номера 120).
Решение
.
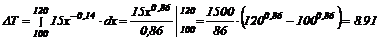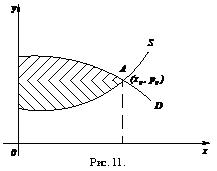
Выигрыш потребителей и выигрыш поставщиков. Пусть р = f(x) – кривая спроса D на некоторый товар и р = g(x) – кривая предложения S; А(х0, р0) – точка рыночного равновесия (рис. 11). Некоторые потребители могут заплатить за этот товар цену р > р0. Найдем выигрыш потребителей от установленной цены р0. Разобьем отрезок [0, х0] на п частей и обозначим точки разбиения:
.
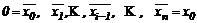На каждом интервале выберем точку 
. Выигрыш потребителей на этом отрезке равен:
(р × (х1*) – р0)×Δхi,
где 
.
Суммируя все выигрыши, получаем:
.
Если функция спроса непрерывна и п ® ¥, а длина максимального отрезка разбиения max ½Δх½ ® 0, то эта интегральная сумма имеет предел, равный:
.
Таким образом, выигрыш потребителей:
.
Аналогично находится выигрыш поставщиков:
.
Очевидно, что выигрыш потребителей равен площади, заключенной между кривой спроса D и прямой р = ро. Выигрыш поставщиков равен площади, заключенной между прямой р = ро и кривой предложения S (см. рис. 11).
Задача 3
Известны законы спроса и предложения:
р = 116 – х 2,
.
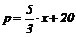Найти выигрыш потребителей и выигрыш поставщиков, если было установлено рыночное равновесие.
Решение.
Найдем точку рыночного равновесия:
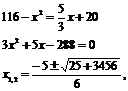
откуда 
– не удовлетворяя 
Среднее значение. Среднее значение непрерывной функции на промежутке [a, b] находится по формуле
Среднее значение функции используется при вычислении налога на имущество предприятия. Величина налога
где k – коэффициент, зависящий от вида предприятия; f(c) – среднее значение стоимости имущества за год; [a, b] – промежуток времени, равный году.
Интеграл вычисляется приближенно по формуле трапеций с разбиением года на 12 месяцев:
где f(0) – стоимость имущества на 1 января; f(1) – стоимость имущества на 1 февраля; … f(11) – стоимость имущества на 1 декабря; f(12) – стоимость имущества на 1 января следующего года.
Задача максимальной прибыли. В ряде отраслей промышленности, например в горнодобывающей, после некоторого момента времени прибыль начинает убывать. В этом случае необходимо найти момент времени, в который прибыль принимает максимальное значение, и своевременно остановить производство.
Задача 4
Скорости изменения издержек и дохода во времени имеют следующий вид:
С¢(t) = 2 + t,
R¢(t) = 17 – 2t.
Найти максимальное значение прибыли, которое можно получить от этого производства. Когда производство следует остановить?
Решение
P¢(t) = R¢(t) - C¢(t) = 17 – 2t – 2 = 15 – 3t,
R¢(t) = 0 при t = 5,
P²(5) = -3 < 0, следовательно, t = 5 – точка максимума,
.
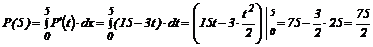Изменение капитала. Если I(t) – скорость изменения инвестиций, а A(t ) – капитал предприятия, то:
.
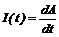Зная скорость изменения инвестиций, можно найти изменения капитала по формуле:
.
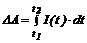Задача 5
Функция предельных издержек имеет вид:
С'(х) = 50 + 0,02х.
а) Найти функцию издержек, если фиксированные издержки составляют 2500 руб в месяц.
б) Каковы издержки производства 250 изделий в месяц?
в) Если продукция продается по цене 75 руб за изделие, сколько нужно произвести и продать, чтобы прибыль была максимальной?
Задача 6
Функция предельных издержек некоторого предприятия имеет вид: С'(х) = 60 - 0,04х + 0,00Зх2.
а) Найти функцию издержек, если издержки производства 100 единиц продукции составляют 7000 руб.
б) Найти фиксированные издержки.
в) Каковы издержки производства 250 единиц продукции?
г) Если цена составляет 65,5 руб за единицу продукции, найти максимальное значение прибыли.
Задача 7
Функция предельных издержек имеет вид:
С'(х) = 60 + 0,04х.
Фиксированные издержки составляют 1800 руб в месяц, а цена одного изделия равна 80 руб.
а) Найти переменные издержки.
б) Каковы издержки производства 150 изделий?
в) Найти приращение прибыли, если объем производства вырос со 150 до 200 изделий.
Задача 8
Функция предельного дохода некоторого предприятия имеет вид:
a) R'(х) =20 - 0,02х, б) R'(х) =,04х - 0,003х2.
Найти функцию дохода. Найти уравнение спроса.
Задача 9
Функция предельной прибыли имеет вид:
Р'(х) =,004х.
Прибыль предприятия составляет 35800 руб, если продано 1200 изделий. Найти функцию прибыли.
Задача 10
Распределение дохода в некоторой стране определяется кривой Лоренса:
а ) у = 0,87х2 + 0,13х; 6) у = 0,96х2 + 0,04х.
Какую часть дохода получают 8 % наиболее низко оплачиваемого населения? Посчитать коэффициент неравномерности распределения совокупного дохода.
Задача 11
Уравнение спроса на некоторый товар имеет вид:
Р = 112 - х2.
Найти выигрыш потребителей, если равновесная цена равна 90.
Задача 12
Уравнение спроса на некоторый товар имеет вид:
.
Найти выигрыш потребителей, если равновесное количество товара равно 10.
Задача 13
Функция совокупных издержек монополии и уравнение спроса на этот товар имеют следующий вид:
а) С(х) = 900 + 40х + 5х2; б) С(х) = 400 + 30х + х2;
р = х - 2х2; 
.
Найти выигрыш потребителей в точке, где монополия имеет максимальную прибыль.
Задача 14
Функция совокупных издержек производства некоторой продукции имеет вид:
С(х) = 1000 + 2х + 0,004х2.
Найти среднее значение издержек при изменении объема производства от 100 до 200 единиц.
Задача 15
Найти прирост капитала предприятия на данном промежутке времени, если скорость изменения инвестиций имеет следующий вид:
а)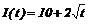 
, 9 £ t £ 16;
б)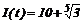 
, 0 £ t £ 1.
4. Применение дифференциальных уравнений
Эластичность и функция спроса. Если известна эластичность спроса на некоторый товар, то можно найти функцию спроса.
Задача 1
Эластичность 
для любых значений р. Найти функцию спроса.
Решение
Пользуясь определением эластичности:
,
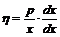получаем дифференциальное уравнение с разделяющимися переменными:
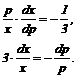
Интегрируем и получаем уравнение спроса:
,
,
px3 = C.
Примечание. Для определения С нужна дополнительная информация.
Функции спроса и предложения. В простейших случаях предполагается, что спрос и предложение на рынке зависят только от цены товара. В более сложных моделях учитывается их зависимость и от изменения цены, т. е. от производной. При этом для определения равновесной цены используется дифференциальное уравнение.
Задача 2
Функции спроса и предложения на некоторый товар имеют вид:
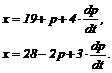
Найти зависимость равновесной цены от времени t, если в начальный момент времени цена р = 20.
Решение
, 
,
, 
, 
,
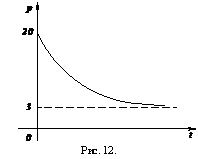
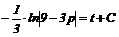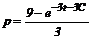Подставляя начальное условие, находим С:
, 
, 
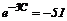– решение задачи (рис. 12).
Так как 
, имеет место устойчивость. Если 
то равновесная цена растет и имеет место инфляция.
Задача 3
Найти функцию спроса, если эластичность h постоянна и задано значение цены p в некоторой точке x:
а) h = -2, p = 10 при x = 4; б) 
p = 15 при x = 1;
в) 
p = 5 при x =2; г) h = -3, p = 2 при x = 27.
Задача 4
В городе с населением 3000 чел. распространение эпидемии гриппа подчиняется уравнению
где у – число заболевших в момент времени t. Через какое время заболеет 70 % населения, если в начальный момент времени было трое больных?
Задача 5
Численность населения y(t) некоторой страны удовлетворяет дифференциальному уравнению:
где время t измеряется в годах. В начальный момент времени население составляло 1000 чел. Через сколько лет население возрастет в четыре раза?
Задача 6
Пусть функции спроса и предложения на некоторый товар имеют вид:
а) Найти зависимость равновесной цены от времени, если p = 10 в момент времени t = 0.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 |
