Математическое моделирование производственного и финансового менеджмента

УДК 330.4:519.8

С126

Рецензенты: Доктор экономических наук, профессор, Новосибирский государственный технический университет Доктор физико-математических наук, профессор, Институт вычислительной математики и математической геофизики СО РАН Савиных, В. Н. С126 Математическое моделирование производственного и финан­сового менеджмента [Текст]: учеб. пособие / . - Новосибирск: СГГА, 20с.

18ВЫ 3253-2

Учебное пособие составлено для студентов 3 и 4 курсов специальности 080507 «Менеджмент организации» и направления 0890500 «Менеджмент», со­держит теоретические положения и методику выполнения индивидуальных расчетно-графических и лабораторных работ по темам математического моделиро­вания производственного и финансового менеджмента. На примерах решения ти­повых задач изучаются методы оптимизации управления производством, ком­мерцией и финансами, а также показываются приемы компьютерной реализации соответствующих моделей в среде ЕХСЕЬ.

Главной целью учебного пособия является оказание методической помощи в самостоятельном решении студентом предложенного ему индивидуального на­бора задач по всем темам курса «Экономико-математические методы».

Печатается по решению редакционно-издательского совета СГГА

УДК 330.4:519.8

© ГОУ ВПО «Сибирская государственная

18ВЫ 3253-2 геодезическая академия», 2007

•  потребители: отдельные лица или группы лиц с общим доходом, расходуемым на потребление;

•  фирмы: предприятия, производящие товары или услуги для про­дажи другим фирмам или конечным потребителям;

•  профессиональные союзы: группы людей, работающих по найму;

•  правительственные организации: политические учреждения, обла­дающие важными экономическими функциями;

•  банки, товарные и фондовые биржи.

Приведенный список не претендует на полноту, так как его всегда можно расширить. Например, моделируемой экономической (организаци­онно -технической) системой может являться филиал производственной фирмы, рассматриваемый отдельно как ее подсистема при взаимодейст­вии с другими филиалами-подсистемами.

Модель - материальный или идеальный объект-копия, создаваемый для решения возникшей проблемы сведением ее к уже известной задаче либо с целью получения новых знаний об объекте-оригинале, выделенном из проблемной среды и отображающем существенные (с позиции разра­ботчика) свойства оригинала [7].

По форме отображения объектов проблемной среды модели принято разделять на две группы: материальные (физические, химические, биоло­гические, аналоговые) и идеальные (знаковые и мысленные). Знаковые модели, в свою очередь, подразделяются на графические (схематические), логико-описательные, математические и компьютерные. Материальные и знаковые модели можно разделить следующим образом:

•  изобразительные (в которых, изменяется только геометрический масштаб модели относительно объекта);

•  аналоговые (в которых, кроме изменения масштаба, происходит за­мена одного свойства, например, глубины или высоты, на другое, напри­мер, синий или коричневый цвет) [31].

Под математической моделью на общетеоретическом уровне нужно понимать такую модель, которая использует для описания свойств и ха­рактеристик объекта или события математические символы и методы [32].

«Экономико-математическая модель (ЭММ) - это описание, ото­бражающее экономический процесс или явление с помощью одного или не­скольких математических выражений (уравнений, функций, неравенств, то­ждеств), имитирующих (отображающих) поведение моделируемого объекта в заданных или возможных условиях его реального существования» [33].

Компьютерная модель - знаковая модель, записанная (без синтакси­ческих ошибок) ее составителем в форме, которую компьютер способен распознать и преобразовать в электрические сигналы для того, чтобы про­извести над ними арифметические и логические действия, а затем (с помо­щью обратного преобразования электрических сигналов в числовую и зна­ковую форму) выдать результат на языке, понятном человеку [30].

При рассмотрении математических моделей экономического объекта, для которых затем создается их компьютерный аналог, следует обратить внимание на два вопроса, сопровождающих изучение моделируемого объ­екта или процесса: управляем ли он исследователем, и возможно ли по­строить такую его модель, которая имела бы аналитическое, а не числен­ное итерационное решение.

Ответ на первый вопрос позволяет определить принадлежность эко­номического объекта и, следовательно, его модели к типу управляемых или только наблюдаемых.

«Существуют два метода получения с помощью модели оптимального решения (или некоторого приближения к нему): аналитический и численный. Аналитические процедуры сводятся к использованию математического ме­тода дедукции. <...> Аналитические решения получаются в абстрактном, символьном виде, т. е. подстановка чисел вместо символов обычно производится уже после того, как будет получено решение.

Численные процедуры состоят в подборе различных значений для управляемых переменных модели, сопоставлений полученных данных и выборе того набора значений, который дает наиболее выгодное реше­ние Такие процедуры могут варьироваться в широком диапазоне от про­стого метода проб и ошибок до сложных итераций» [31].

Классификация моделей по ответу на второй вопрос помогает уточнить, принадлежит ли модель к типу численных итерационных либо аналитических.

Численные итерационные модели решаются методами, которые многократно выполняют этапы вычислений по одной и той же схеме до тех нор, пока не выполнится заранее заданное условие остановки вычис­лительного процесса.

Аналитические модели характерны наличием готовой функции, со­стоящей из одной или нескольких формул («ответов»), вычисление по ко­торым можно выполнить за один этап.

В свою очередь, управляемые модели подразделяются на два типа: оптимизационные и неоптимизационные.

Цель разработки оптимизационных управляемых моделей при наличии многих вариантов допустимых управляющих решений заклю­чился в получении такого решения, которое максимально увеличит ли­бо уменьшит уровни приоритетных показателей. Например, в матема­тических моделях рыночной экономики в подавляющем большинстве случаен решение принимается на основе стоимостного показателя, как модельного критерия, и поэтому сводится или к максимизации доходов, или к минимизации затрат.

Цель разработки неоптимизационных управляемых моделей состо­ит, и частности, в стабилизации управляемых систем, т. е. в превращении (с помощью этих моделей) изначально неустойчивых систем в устойчи­вые. Эти модели предоставляют возможность выбора приемлемого вари­анта функционирования системы, исходя из внемодельных соображений. Неоптимизационные управляемые модели, если они являются численны­ми, называют обычно имитационными.

Если же изучаемая экономическая система настолько сложна, что не может быть описана ни аналитической, ни численной оптимизационной моделью, то исследователю не остается ничего другого, как составить ее имитационную модель. Затем эта модель переводится с языка математики на язык информатики для проведения на ней соответствующих компью­терных имитационных экспериментов.

Часто как оптимизационные, так и неоптимизационные численные модели в литературе называют имитационными, хотя желательно выде­лить какой-то специальный термин для обозначения неоптимизационных имитационных моделей. Такая терминологическая неустойчивость объяс­няется чрезвычайной трудностью решения оптимизационных задач мето­дами имитационного моделирования.

Проблема соответствия (адекватности) математических моделей эко­номики реальностям экономической жизни в большинстве случаев зави­сит не от ошибочности решения математической задачи, в которую была преобразована словесная формулировка, а от правильности самого этого преобразования.

«Математика, - отмечает во введении к своей монографии Р. Ален, - является путеводителем от предпосылок к выводам, но сами эти предпо­сылки могут быть любой совместной системой кем-то сформулированных аксиом. Теории возникают лишь из особого содержания предмета незави­симо от того, идет ли речь об экономике или электротехнике. <...> Не до­пуская логической ошибки, можно сказать, что выводы будут верны, если предпосылки правильны. Но это не является доказательством какой-либо теории, ни в экономике, ни в какой-либо другой области знаний. Теории проверяются фактами: либо проверяются предпосылки, либо, что бывает чаще, - выводы» [1].

Например, причиной ошибочных результатов могут оказаться какие-либо из начальных экономических предположений словесной модели. Эта причина относится не только к моделям математической экономики, но к математическим моделям вообще. Основная трудность, преодоле­ваемая на этапе математического моделирования, заключается не в оши­бочных начальных условиях (ограничениях), накладываемых на перемен­ные, а выборе самих этих переменных.

«На практике исходным пунктом часто является некоторая эмпириче­ский ситуация, выдвигающая перед исследователем «задачу», на которую требуется найти «ответ». Однако, употребление таких слов, как «задача» и мотет» не должно вводить в заблуждение. Прежде всего, необходимо установить, в чем именно заключается «задача». Это замечание связано с тем, •но реальные ситуации редко бывают четко очерченными, а сложное взаимодействие с окружающей средой делает точное описание ситуации затруднительным. Процесс выделения «задачи», поддающийся математи­ческому анализу, часто бывает продолжительным и требует владения мно­гими навыками, не имеющими никакого отношения к математике (напри­мер, беседы с коллегами-нематематиками, работающими в данной об­ласти, и чтение всевозможной литературы, имеющей отношение к делу, являются важным элементом процесса моделирования).

Способность увидеть, что рассматриваемая ситуация принадлежит к известному классу задач, для которого имеются стандартные теории, - по искусство, имеющее для моделирования огромное значение. В этом как бы фокусируется вся суть прикладной математики, а именно, что один и гот же математический аппарат может описывать очень широкий круг ре-ильных ситуаций, которые сами по себе могут казаться совершенно не связанными друг с другом» [17].

Одной и той же математической (аналитической или численной, на-(1.И1.К-М0Й также алгоритмической) модели могут соответствовать разнообразные компьютерные модели, т. е. ее реализации в различных программных средах. Однако, из-за своей общедоступности в программном и методическом смысле, необязательности знания языков программирование; а также из-за относительной математической прозрачности, более мест для учебного процесса подходит программная среда ЕХСЕL.

Такой математически закрытый инструмент для экономистов-практиков, как универсальная или специальная компьютерная программа, созданная для моделирования, как правило, устаревает либо вместе с опе­рационной системой, на базе которой она была написана, либо вместе с по­колением компьютера, на котором она программировалась. В отличие от него, относительно прозрачный математический инструментарий среды ЕХСЕL значительно менее изменчив (инвариантен) во времени.

Общеизвестно, что выпускник экономического вуза или факультета, получающий квалификацию «менеджер», должен уделять достаточное внимание усвоению как математических, так и компьютерных средств поддержки принятия управляющих решений. В данном пособии для моде­лирования принятия оптимальных решений используются математические средства, основой которых являются методы оптимизации или методы ма­тематического программирования, а привлечение компьютерных средств демонстрируется на примерах экономического моделирования в ЕХСЕЬ.

Нужно особо подчеркнуть приоритет математического моделирования, как этапа, предшествующего компьютерному моделированию. Студенты часто пренебрегают выполнением этого важного этапа между словесной формулировкой задачи и ее решением на персональном компьютере. Мно­голетняя практика преподавания показала, что студенты, пытающиеся ми­новать этап математического моделирования в переходе от словесной фор­мулировки задачи к записи данных в ячейки электронной таблицы, в подав­ляющем большинстве случаев, не получают правильного решения.

Основным содержанием предлагаемого учебного пособия в свете приведенной выше классификации являются управляемые оптимизацион­ные модели, которые относятся к типу численных итерационных моделей и используются как инструментарий для анализа задач производственного и финансового менеджмента.

Каждая тема пособия начинается с описания типовой ситуации, взя­той из производственной, финансовой или коммерческой сферы экономи­ки. При этом приводится словесная формулировка свойств оптимального управляющего решения для данной ситуации. Затем осуществляется пере­вод словесной формулировки на язык символов и, в конечном итоге, со­ставляется математическая модель расчета параметров оптимального управляющего решения. Исходные данные, предложенные в индивиду­альных заданиях и упражнениях, сгенерированы таким образом, чтобы со­ставленная на их основе математическая модель могла быть решена соот­ветствующим методом оптимизации без помощи компьютера.

Автор стремился сделать так, чтобы при выполнении ручных рас­четов по изучаемому методу оптимизации студент избежал ненужной рутинности вычислений, но полностью усвоил идею метода. Например, в тех случаях, когда компьютер стал бы применять итерации симплекс-алгоритма для выхода на оптимальное решение, при ручных расчетах предлагаются использовать графический способ определения оптимального решения задачи линейного программирования с двумя переменными. По убеждению автора, обязательные решения составленных моделей вручную нужны для более глубокого осмысления использованных при моделировании теоретических положений.

С другой стороны, каждая экономико-математическая модель, рассматриваемая в пособии, может быть легко переформулирована для прак­тически значимой размерности. Понятно, что решение такой модели мож­но будет получить, только используя ее компьютерный аналог. Из-за ограниченных рамок пособия только для четырех из десяти рассмотренных экономико-математических моделей показано создание их компьютерных аналогов в среде ЕХСЕL и приведен анализ результатов расчетов по ним.

Последовательность тем пособия соответствует порядку их прохо­ждения по рабочей программе курса «Экономико-математические ме­тоды», причем, первые три темы являются базовыми, на которые, так или иначе, опираются все последующие темы. По нашему мнению, эф­фективное изучение математических моделей менеджмента должно проходить в следующей последовательности: 1) модели линейного программирования, 2) модель сетевого планирования и управления, 3) модель матричной игры, 4) модель частично целочисленного программирова­нии, 5) модель дробно-линейного программирования и 6) модели нели­нейного программирования.

1. МОДЕЛИРОВАНИЕ ОПТИМАЛЬНОГО УПРАВЛЯЮЩЕГО РЕШЕНИЯ ЗАДАЧЕЙ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

1.1. Составление математической модели расчета оптимальной производственной программы

Чтобы процесс составления математической модели расчета опти­мальной производственной программы предприятия изложить проще и в более доступной форме, рассмотрим его на конкретном примере.

Для изготовления двух видов продукции А и Б предприятие расходует три вида ресурсов: сырье, оборудование и труд. Информация о нормах за­трат ресурсов на единицу выпускаемой продукции, лимиты ресурсов, на которые рассчитывает предприятие в плановом периоде, и рыночные цены реализации каждой единицы продукции приведены ниже.

Наименование Норма затрат на Объем Ц

ресурса продукт А продукт В ресурса г\

Сырье (кг

Оборудование (ст.-ч

Труд (чел.-ч

Цена реализации (руб.) 50 70

Задача администрации предприятия заключается в разработке такой программы выпуска продукции в плановом периоде, затраты ресурсов на которую не превысят имеющихся лимитов, а ожидаемая выручка после продажи выпущенной продукции будет максимальной.

Требуется:

1.  Составить экономико-математическую модель расчета оптимальной! производственной программы предприятия на плановый период.

2.  Применяя графический метод решения задачи линейного програм­мирования, найти оптимальное решение для составленной модели и дать его экономическую интерпретацию.

3.  Используя положения теории двойственности, найти оптимальное решение двойственной задачи к модели расчета оптимальной производст­венной программы и привести его экономическую интерпретацию.

4 Определить функцию предельной эффективности сырья на этом предприятии и функцию зависимости максимальной выручки от затраченного сырья, построить графики этих функций.

Для построения экономико-математической модели заданной проиводственной ситуации обозначим через х, искомую программу выпуска изделий А, а через х2 - искомую программу выпуска изделий В.

Тогда производственная программа полностью будет представлена вектором

х =(х/,х2).

Эти программа должна выбираться с учетом объемов имеющихся ре­сурсом и рассматриваемом периоде.

Суммарный расход сырья на производственную программу, рассчитываемый по формуле 1х1 + 2х2, не должен превысить 40 кг сырья. Отсюда ограничение на расход сырья представится неравенством

1х, +2х2 ≤40.

Общая загрузка оборудования на производственную программу рассчитывается по формуле 2х, +1х2, и эта загрузка не должна превысить 50 ст.-ч. работы оборудования. Отсюда получаем ограничение на работу оборудования:

2х, + 1х2 < 50.

Суммарные затраты труда на производственную программу рас­считываются по формуле 1х, + 1х2, и эти затраты не должны превысить 35 чел.-ч. Отсюда получаем ограничение на затраты труда:

1х, + 1х2 <35.

Кроме того, для искомых переменных х1, х2 должны выполняться граничные условия (или требования неотрицательности), а именно:

х, >0; х2 >0.

Показателем качества выбранной производственной программы яв­ляется ожидаемая выручка от реализации всех выпущенных изделий. Эту выручку необходимо рассчитывать по формуле

z = 50х1+70х2.

Искомая программа должна максимизировать сумму z, которая также называется целевой функцией, или критерием оптимизационной модели. Символически требование максимизации отражается записью

z = 50х, + 70х2→ тах.

Представим составленную модель в следующей компактной записи:

Найти х=(х1,х2),

х, + 2х2 < 40;

2x1 +х2 <50; (1.1)

x1 +х2 = 35;

х, >0; х2 >0;

z = 50x1 + 70х2 → тах.

Модель (1.1), представленная такой записью ограничений, граничных условий и целевой функции, относится к типу задач линейного программирования. Термин «линейное программирование» объясняется тем, что при подсчете расходов ресурсов на программу выпуска и расчете ожидае­мой выручки после реализации всей выпущенной по этой программе про­дукции используются только линейные функции.

В общем случае задача линейного программирования может быть пред­ставлена в так называемой стандартной записи. Известно, что к стандартной записи можно привести задачу линейного программирования (задачу ЛП), данную в любой другой записи, используя для этого специальные правила эквивалентных преобразований. Поэтому во всех дальнейших утвержде­ниях, без потери общности, под задачей ЛП будем понимать ее стандарт­ную постановку (1.2).

Найти x = (x1,...,xj,...,xn),

а11х,+... + а1jхj+... + а1пхп ≤b1,

а i1х1+... + аijхj +... + аiпхп ≤ bi;

а1тх1 +... + аmj хj+... + атпхп≤ bm;

x j≥0, j=1,n;

z=c1 x1 +…+сj хj +…+ спхп →max

1.2. Графический метод решения задачи линейного программирования

11олыуясь тем, что в задаче ЛП (1.1) имеется две искомые переменные, ее можно решить графическим способом, который состоит из следующих двух этапов.

1. Изображение области допустимых решений предложенной задачи ЛП в декартовой системе координат.

2. Визуальное нахождение оптимального решения на построенной области допустимых решений и его аналитическое уточнение.

Выполним названные этапы для задачи (1.1).

1. Под допустимым решением задачи ЛП понимается такой числовой набор значений искомых переменных, который при подстановке во все ограничения и граничные условия задачи обращает их в истинные числовые неравенства и равенства. Под областью допустимых решений (ОДР) задачи ЛП понимается геометрическое место точек, координаты которых являются допустимыми решениями.

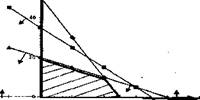
Прежде всего, укажем в декартовой системе координат на рис. 1.1 область допустимых решений для первого ограничения задачи (1.1). Для этого проведем в системе координат прямую, соответствующую первому ограничению. Уравнение этой прямой будет получено, если первое огра­ничение будет записано как равенство

х] + 2х2 =40.

Рис. 1.1. Построение области допустимых решений задачи ЛП

Задавая произвольно значение одной из координат точки, лежащей на этой прямой, можно через полученное уравнение вычислить значение другой координаты этой же точки. Если данная прямая имеет точки пере­сечения с обеими осями в пределах создаваемого рисунка, то лучше при­сваивать нулевое значение сначала первой переменной, затем второй пе­ременной, находя соответствующее значение другой переменной.

Результаты этих вычислений рекомендуется заносить в таблицу.

Отметим эти точки на осях рис. 1.1 и проведем через них прямую, со­ответствующую первому ограничению. На рисунке она маркирована тре­угольниками. Если взять координаты любой точки, лежащей на этой пря­мой, то они обратят первое ограничение в равенство. Для выявления то­чек, координаты которых строго удовлетворяют данному ограничению, нужно указать на одну из образовавшихся полуплоскостей.

Для определения полуплоскости, координаты точек которой являются строгими решениями данного неравенства, необходимо выбрать пробную точку, явно принадлежащую какой-либо из двух полуплоскостей, полу­ченных после проведения прямой, соответствующей этому неравенству.

Если координаты пробной точки обращают неравенство в истинное числовое неравенство, то полуплоскость, которой она принадлежит, явля­ется искомой. На рис. 1.1 искомые полуплоскости выделены стрелками, Если числовое неравенство получилось ложным, то стрелками нужно ука­зать полуплоскость, которой не принадлежит пробная точка.

Таким образом, с помощью одной пробы графически выявляется об­ласть допустимых решений для любого из ограничений и граничных усло­вий анализируемой задачи ЛП.

В тех случаях, когда прямая не проходит через начало координат, в качестве пробной точки проще всего брать значения: х, =0, х2 = 0. Подставим эти значения в анализируемое неравенство и, получив утверждение 0<40, находим его истинным. Поэтому стрелки от этой прямой откладываем в направлении начала координат, показывая тем самым, где лежат все точки, координаты которых являются допустимыми решениями для ограничения по сырью.

Подобным образом следует поступить с каждым ограничением и гра­ничным условием задачи ЛП, выделив стрелками пять соответствующих ИМ полуплоскостей на одном и том же рисунке. При этом прямая, марки-|нп11чмшн ромбами, соответствует второму ограничению и имеет следую­щие координаты точек пересечения с осями:

Прямая, помеченная квадратами, соответствует третьему ограничению задачи и пересекается с осями в точках с координатами:

Следующим шагом нужно выделить общую часть обозначенных эти­ми стрелками полуплоскостей или, другими словами, найти их пересечение. На рис. 1.1 заштрихованный четырехугольник с выделенными жирной линией сторонами представляет собой все множество точек, координаты которых обращают в истинные утверждения все ограничения и гра­ничные условия модели. Это означает, что первый этап завершен, и область допустимых решений задачи ЛП построена. Полезно обратить внимание на то, что, если третье ограничение исключить из модели, то ОДР останется неизменной. Такое нельзя сказать о других ограничениях модели.

2. Под оптимальным решением задачи ЛП понимается такое допустимое решение, при котором целевая функция задачи принимает экстремальное значение (максимальное или минимальное). Доказано, что среди множества оптимальных решений задачи ЛП, если они есть у этой задачи, общительно существуют координаты вершины или угловой точки много­угольной области допустимых решений задачи ЛП (ограниченной или не­ограниченной). Набор числовых значений координат угловой точки ОДР называется опорным решением задачи ЛП. Другими словами, среди множества оптимальных решений задачи ЛП всегда существует подмножество опорных решений.

Выделенному на рис. 1.1 четырехугольнику допустимых решений соответствуют четыре опорных решения - четыре варианта координат угловых точек: х1 = (0, 0), х2 = (25, 0), х3 = (20, 10), х4 =(0, 20). Коор­динаты угловой точки х3 =(20, 10) можно найти, вычислив координаты точки пересечения прямых, маркированных треугольниками и ромбами для чего нужно решить систему уравнений

х1 + 2х2 = 40;

2 х1+х2 =50.

Для визуального выявления оптимального решения среди этих опорных решений используем следующие теоретические понятия.

Под линией уровня целевой функции понимается геометрическое место точек, для координат которых зависимая переменная z имеет постоянное числовое значение.

Например, уравнение линии нулевого уровня будет иметь вид:

0 = 50 х1+ 70х2;

или уравнение линии уровня 100 будет иметь вид:

100 = 50х1+70х2;

или уравнение линии уровня 1000 будет иметь вид:

1000 = 50 х1 +70х2.

Очевидно, что для всех возможных числовых значений линии уровня целевой функции являются прямыми, которые будут параллельными между собой и покрывать всю плоскость.

Под градиентом целевой функции понимается вектор с началом в текущей точке плоскости х = (х1,х2), координаты которого рассчитываются, как значение частных производных целевой функции z в этой точке:

gradZ(x)=(∂z /∂ х1 ; ∂z /∂ х2).

Градиент целевой функции обладает двумя характерными свойствами:

1. он перпендикулярен линиями уровня целевой функции.

2. он указывает сторону наискорейшего роста целевой функции.

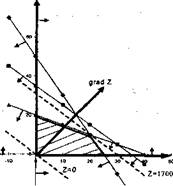
Используем изложенные выше теоретические положения для нахождения точки оптимального решения на построенной области допустимых решений. Вычислим градиент целевой функции z = 50 х1+70х2 в текущей точке х по формуле (1.3) и получим

gradZ(x) = (50, 70).

Очевидно, что в случае линейной целевой функции, направление градиента не зависит от текущей точки, от которой он откладывается.

Дни того чтобы уложиться в заданный масштаб, отложим от начала координат на рис. 1.2 вектор с такого же направления, как и вычисленный градиент, но вдвое меньший по длине, то есть с = (25, 35). Затем, соглас­но названному выше свойству градиента, проведем через начало координат перпендикулярно градиенту линию нулевого уровня. На рис. 1.2 она изображена пунктирной линией, которая используется как начало отсчета для роста уровня целевой функции.

рис. 1.2. Визуальное определение оптимального решения на построенной области допустимых решений

Определим наиболее удаленную в направлении градиента линию уровня, имеющую общую точку с областью допустимых решений. Такой пинии уровня соответствует пунктирная прямая, проходящая через точку ОДР с координатами (20,10). Значит, в этой точке достигается максимально значение уровня целевой функции над построенной областью допустимых решений, которое легко вычисляется подстановкой координат точки в целевую функцию

zmax= 50 ∙20 + 70 ∙ 10 = 1700.

Отсюда оптимальным решением задачи является х*1 =20, х*2 = 10.

Правильному визуальному определению оптимальной точки ОДР может помешать погрешность сделанных графических построений, пример, при повороте градиента чуть вправо по часовой стрелке, линия уровня при движении в новом направлении покинет последней уже точ­ку ОДР с координатами (25, 0). В целях аналитической подстраховку графически найденного оптимального решения вычислим значение целевой функции в этой точке

z= 50 ∙25 + 70∙ 0 = 1250.

Так как 1 250 < 1 700, то это подтверждает правильность найденного визуально оптимального решения задачи (1.1).

В качестве экономической интерпретации найденного оптимально го решения предлагается сделать вывод, что оптимальной производственной программой предприятия в плановом периоде будет выпуск первого продукта в объеме 20 единиц и второго продукта в объеме 10 единиц. При этом предприятие получит ожидаемую максимальную выручку размере 1 700 руб.