Таблица 9.3

Основные виды программных документов

10. Разработка программной документации

На рис. 10.1 представлена схема разработки и использования программной документации. Техническое задание и пояснительная записка к нему разрабатываются на этапе постановки задачи. Фактически они являются результирующими (выходными) документами данного этапа. В них фиксируются требования к разрабатываемой программе. Если заказчик и разработчик программы работают в разных организациях, техническое задание становится обязательной частью договора.

В отличие от пояснительной записки, техническое задание должно содержать четко сформулированные, поддающиеся контролю требования к разрабатываемой программе. В дальнейшем, при тестировании программы и принятии решения о ее работоспособности, именно техническое задание будет определять требования, подлежащие контролю.

На этапе разработки формируется текст программы (исходный код) и описание программы. На заключительном этапе разработки формируется система контекстной подсказки (Help) и Руководство пользователя. Текст программы используется при регистрации программы как объекта интеллектуальной собственности. При этом он полностью или частично депонируется[12]. В случае возникновения споров об авторстве программы агентство, в котором зарегистрирована программа, предоставляет в арбитраж[13] копию исходного кода для установления авторства. Именно поэтому свои программы стоит подписывать!

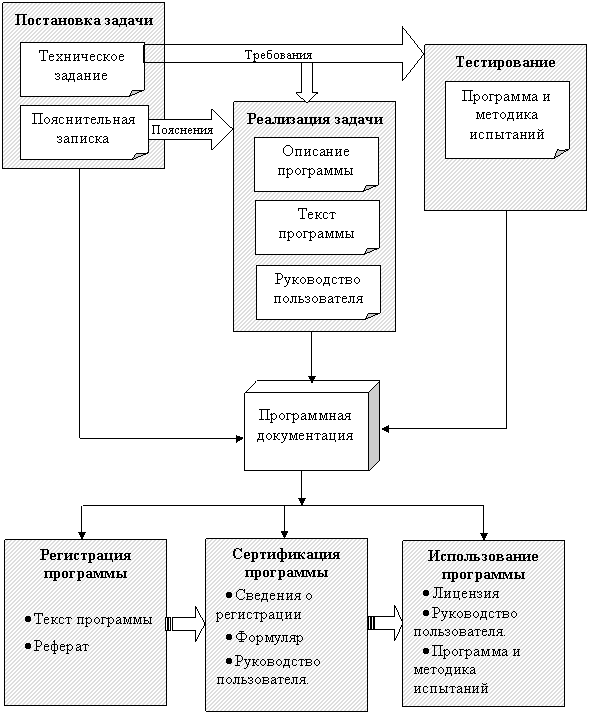
Рис. 10.1. Схема создания и использования программной документации

Для проведения тестирования разрабатывается специальный документ: «Программа и методика испытаний». В документе перечисляются требования к программе, которые необходимо проверить. Перечень требований определяется Техническим заданием, а также стандартами или особыми требованиями, записанными в договоре. Для каждого требования описывается методика, по которой это требование должно быть проверено и критерий соответствия программы предъявленному требованию.

Например. В техническом задании записано требование: «Программа должна работать под операционными системами Windows 98, 2000, NT4, ME, XP». Методика проверки выполнения этого требования должна заключаться в следующем: Мы инсталлируем программу на компьютерах, работающих под каждой из перечисленных операционных систем. Критерий соответствия программы требованию: успешная (без сбоев и зависаний, корректная) работа программы под каждой операционной системой.

Документ «Программа и методика испытаний» может быть использован и при сертификации программы.

Если авторы программы по собственному желанию или по требованию Заказчика решают зарегистрировать ее как объект интеллектуальной собственности, они подготавливают документацию в соответствии с требованиями двух документов:

־  «Правила составления, подачи и рассмотрения заявок на официальную регистрацию программ для электронных вычислительных машин и баз данных»

־  «Рекомендации по оформлению материалов заявки на регистрацию программы для ЭВМ (базы данных)».

Оформленные заявка и документация посылаются в отдел регистрации программ для ЭВМ, баз данных и топологий ИМС ФИПС.

При успешной регистрации программы, авторам выдается свидетельство о регистрации. Свидетельство дает право:

·  продавать программу целиком – без права использовать ее самому и продавать еще раз. Такое право оформляется исключительной лицензией;

·  продавать право использование программы одному или многим пользователям с правом пользоваться самому. Это неисключительная лицензия,

·  дарить или безвозмездно уступать программу кому угодно.

Таким образом, регистрация программы закрепляет за автором права собственности и позволяет ему извлечь из использования программы коммерческую выгоду.

Пример разработки комплекта документов. Решение квадратного уравнения

Особенности разработки комплекта программной документации рассмотрим на примере программы, предназначенной для знакомства школьников с методами решения квадратного уравнения[14].

Результаты постановки задачи зафиксируем в документах: «Пояснительная записка» и «Техническое задание». В Пояснительной записке опишем идею программы, а в Техническом задании сформулируем основные требования к программе.

Пояснительная записка

Введение.

Наименование программы: “Решение квадратного уравнения“. Программа предназначена для знакомства школьников с методами использования компьютера на примере нахождения корней квадратного уравнения.

Назначение и область применения.

Программа является обучающей. Её цель:

1)  приобщить школьников к использованию компьютера для решения математических задач;

2)  познакомить с теорией квадратного уравнения;

3)  научить решать квадратные уравнения.

Технические характеристики.

Программа должна выдавать результат с сообщением понятным пользователю.

Для решения квадратного уравнения вычисляется его дискриминант (D), после чего находятся корни уравнения ( x1,x2). Если введённые коэффициенты описывают не квадратное, а линейное уравнение (A=0), то находится корень линейного уравнения, о чём сообщается пользователю. В случае если введённые коэффициенты не соответствуют ни квадратному, ни линейному уравнениям (A=0 и B=0), то должно выдаваться сообщение.

При запуске программы пользователю предлагается ввести коэффициенты A,B, C, после чего выдаётся результат в виде сообщения.

Программа написана в среде C++ Builder 6.0 Enterprise. Программа разработана для IBM PC со следующими характеристиками:

1)  процессор Intel Pentium 266 MHz или выше;

2)  объём ОЗУ не менее 64 MB;

3)  наличие установленной операционной системы Windows 98 / NT / 2000 / XP

4)  наличие стандартной клавиатуры;

5)  наличие манипулятора типа ”мышь”

Источники, использованные при разработке.

При написании программы использовалась литература: Учебник математики для седьмого класса средней школы, Методика преподавания математики в средних классах общеобразовательной школы, Руководство по С++ Builder 6.0 Enterprise.

__

______

Введение.

Наименование программы: “Решение квадратного уравнения“. Программа предназначена для знакомства школьников с методами использования компьютера на примере нахождения корней квадратного уравнения.

Назначение и область применения.

Программа является обучающей. Её цель:

4)  приобщить школьников к использованию компьютера для решения математических задач;

5)  познакомить с теорией квадратного уравнения;

6)  научить решать квадратные уравнения.

Технические характеристики.

Программа должна выдавать результат с сообщением понятным пользователю.

Для решения квадратного уравнения вычисляется его дискриминант (D), после чего находятся корни уравнения ( x1,x2). Если введённые коэффициенты описывают не квадратное, а линейное уравнение (A=0), то находится корень линейного уравнения, о чём сообщается пользователю. В случае если введённые коэффициенты не соответствуют ни квадратному, ни линейному уравнениям (A=0 и B=0), то должно выдаваться сообщение.

При запуске программы пользователю предлагается ввести коэффициенты A,B, C, после чего выдаётся результат в виде сообщения.

Программа написана в среде C++ Builder 6.0 Enterprise. Программа разработана для IBM PC со следующими характеристиками:

6)  процессор Intel Pentium 266 MHz или выше;

7)  объём ОЗУ не менее 64 MB;

8)  наличие установленной операционной системы Windows 98 / NT / 2000 / XP

9)  наличие стандартной клавиатуры;

10)  наличие манипулятора типа ”мышь”

Источники, использованные при разработке.

При написании программы использовалась литература: Учебник математики для седьмого класса средней школы, Методика преподавания математики в средних классах общеобразовательной школы, Руководство по С++ Builder 6.0 Enterprise.

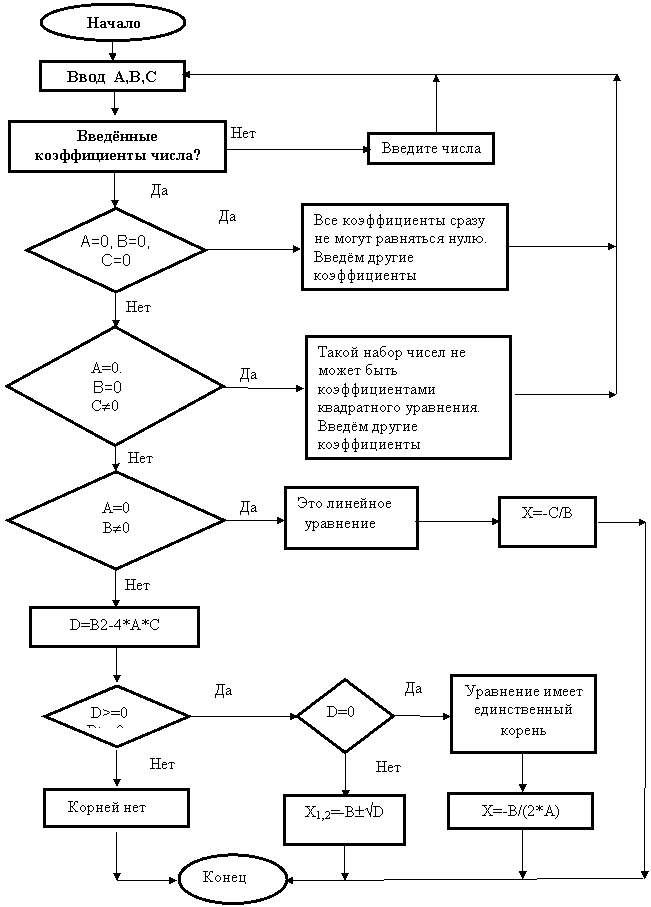
Рис. 10.2. Блок-схема алгоритма программы
ОПИСАНИЕ ПРОГРАММЫ

Общие сведения

Наименование программы: «Решение квадратного уравнения ». Программа предназначена для школьников. Программа может использоваться для обучения школьников приемам работы на компьютере на примере нахождения корней квадратного уравнения. Для написания данной программы использовался язык программирования С++, так как он наиболее удобен и известен авторам.

Функциональное назначение.

Программа является обучающей. Ее цель:

1) приобщить школьников к использованию компьютера для решения математических задач;

2)  познакомить с теорией квадратного уравнения;

3)  научить решать квадратные уравнения.

Программа написана в среде “C++ Builder 6.0 Enterprise”.

Программа работает под управлением операционных систем Windows 98/NT/2000/XP.

Используемые технические средства.

Программа разработана для IBM PC со следующими характеристиками:

·  Процессор Intel Pentium 266 MHz, или выше.

·  Объём ОЗУ не менее 64Mb.

·  Наличие установленной операционной системы Windows 98/NT/2000/XP.

·  Наличие стандартной клавиатуры.

·  Наличие манипулятора типа “мышь”.

Вызов и загрузка.

При установке программы на рабочем столе появляется ярлычок, кликнув на который запускается наша программа. Программа имеет одну входную точку, которой соответствует ввод коэффициентов с клавиатуры.

Входные данные.

При запуске программы появляется персонаж, который предлагает познакомиться:

сообщает своё имя, спрашивает имя пользователя и его возраст. Если возраст школьника меньше 12 лет, то выводиться сообщение: «А не рано ли решать квадратное уравнение?», иначе: «Давай попробуем!» После этого предлагается ввести коэффициенты уравнения в «ячейки ввода» как показано в ниже приведённом примере.

При возникновении каких-либо вопросов пользователь может воспользоваться кнопкой помощи ( ), которая содержит следующую полезную информацию:

квадратное уравнение – уравнение вида: A*x2 + B*x + C = 0,

где х - переменная, А, В, С – некоторые числа (А ¹ 0). А, В и С называются коэффициентами квадратного уравнения. А – первый коэффициент, В – второй коэффициент, С – свободный член.

Если в квадратном уравнении хотя бы один коэффициент равен нулю, то такое уравнение называется неполным квадратным уравнением, которое бывает трёх видов:

1)  А*х² + С = 0 (С < 0);

А*х² = - С;

х² = - С/А;

Если х² = - С/А > 0, то уравнение имеет два решения:

x1=√(-C/A), x2=-√(-C/A),

а иначе ни одного.

2)  А* х² + В*х = 0 (A ¹ 0 и В ¹ 0);

x (А*х + В) = 0;

х = 0 или А*х + В = 0;

x1=0

х2 = - В/А;

3)  А* х² = 0;

х = 0;

Если А = 1, то полученное квадратное уравнение называется приведённым.

Данное уравнение вида:

– х² + р*х + q = 0

можно решить двумя способами: по теореме Виета и через дискриминант.

По теореме Виета: х1*х2 = q

х1 + х2 = - р.

Если дискриминант больше нуля (D > 0), то уравнение имеет два корня, если D = 0, то

один корень, а если D < 0, то уравнение не имеет решения.

Когда В является чётным числом, квадратное уравнение принимает следующий вид:

А* х² + 2*k*х + С = 0;

D1= k² - A*C

x1,2= (-k ±Ö (D1)/A)

После ввода коэффициентов нужно нажать на кнопку

Выходные данные.

При вводе коэффициентов, при которых квадратное уравнение не имеет смысла, выводиться сообщение с разъяснением неправильного выбора коэффициентов и предложением ввести новые коэффициенты. В другом случае выводиться результат с сообщением: «Ты молодец! Вот твой результат»

Затем продолжается диалог со школьником и задаётся вопрос: «Тебе понравилось? Может, решим ещё одно уравнение?» Если пользователь нажимает кнопку «Да», то

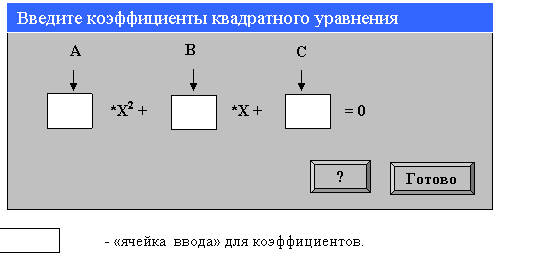
Рис.10.3 Окно ввода данных

возвращается к вводу коэффициентов; если «Нет», то выводиться сообщение: «Ну ладно. Тогда в другой раз. Пока!»

РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ

Назначение программы.

Программа является обучающей. Ее цель:

1) приобщить школьников к использованию компьютера для решения математических задач;

4)  познакомить с теорией квадратного уравнения;

5)  научить решать квадратные уравнения;

6)   

Условия выполнения программы.

Программа разработана для IBM PC со следующими характеристиками:

·  Процессор Intel Pentium 266 MHz, или выше.

·  Объём ОЗУ не менее 64Mb.

·  Наличие установленной операционной системы Windows 98/NT/2000/XP.

·  Наличие стандартной клавиатуры.

·  Наличие манипулятора типа “мышь”.

Выполнение программы.

Для загрузки, запуска, выполнения и завершения программы необходимо осуществить следующие действия:

1) после открытия гибкого диска находимо навести курсор на ярлычок SETUP и дважды нажать левую кнопку «мышки»;

2) происходит запуск программы, и на рабочем столе появляется ярлычок для запуска программы;

3) после запуска программы на экране появляется персонаж. Между школьником и персонажем ведется диалог, в ходе которого предлагается ввести коэффициенты уравнения;

4) нажав кнопку “Готово” выводится либо сообщение о неправильно введенных коэффициентах, либо результат;

5)затем продолжается диалог: пользователю предлагается решить ещё одно уравнение. В случае согласия программа возвращается к вводу коэффициентов, иначе происходит выход из программы.

Сообщения оператору.

В ходе выполнения программы появляются сообщения:

“Введите числа!”

Это сообщение выдаётся в том случае, если пользователь ввел бессмысленные коэффициенты и ему нужно ввести именно числа.

Например : «, . / # % ^ ) ( ! ~ \ $ * № и т. д.»

“Введём другие коэффициенты”

Это сообщение выдаётся в том случае, если пользователь ввел коэффициенты, при которых уравнение не имеет смысла. Это возможно в том случае, если все коэффициенты нулевые.

“<C>не может равняться нулю. Введём другие коэффициенты”

Это сообщение выдаётся в том случае, если коэффициенты “A” и “B” были заданы как нулевые, а значение “ C” отлично от нуля. Т. е. константа “C” не равная нулю, по полученному уравнению должна равняться нулю.

“Это линейное уравнение”

Это сообщение выдаётся в том случае, если при введённых коэффициентах получается не квадратное, а линейное уравнение. Поэтому решением уравнения является единственный корень.

Пример: если A = 0, то получаем линейное уравнение B*X+C=0

“Единственный корень”

Это сообщение выдаётся в том случае, если дискриминант равен нулю, и квадратное уравнение имеет два одинаковых корня.

Например: если D = 0, то X1,2 = - B/2*A

“Корней нет”

Это сообщение выдаётся в том случае, если дискриминант меньше нуля, и уравнение не имеет действительных корней.

Ответы и решения

Основы метрологии

1. Решение. Значение величины вычислим как среднее значение всех замеров. В предположении нормального распределения случайной ошибки погрешность измерения вычислим как утроенное среднеквадратическое отклонение замеров.

Ответ: Х=358,04 ∆Х=0,47

2. Решение: Максимально допустимая погрешность прибора класса точности 0,5 и максимальным значением 10 Вт равна: Δдопуст=10*0,5/100=0,05 Вт. Отклонения значений поверяемого и эталонного приборов приведены в таблице.

Максимальное отклонение =0,041Вт < 0,05 Вт. Следовательно, прибор прошел поверку.

3. Решение: Абсолютная погрешность микроамперметра ∆x= 100μА*1%=1μА. Погрешность косвенного измерения:

.

Максимальное значение производной найдем графически: Максимальный наклон кривой в конце шкалы. При изменении x от от 95 до 100 μА (dx≈5), значение Y изменилось на 2 деления. Между значениями 0 и 2000 на шкале Y находится 5 делений. Следовательно, цена деления этой шкалы=2000/5=400. Вычислим dY ≈ 400*2=800.

Максимум модуля производной dY/dx ≈ 800/5=160. Следовательно, погрешность измерения Y равна

Ответ: Погрешность косвенного измерения 160 ед.

4. Решение: Погрешность косвенного измерения величины V(x1,x2) вычислим методом переноса ошибок.

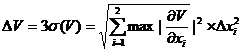
В нашем случае V- скорость, x1 = S – путь, x2 = t –время. . Найдем производные:

час-1; мм/час2

Абсолютная погрешность прямого измерения пути ∆S=0,1 мм. Погрешность измерения времени задана в сек/сутки. Найдем абсолютную погрешность ∆t за время измерения:

∆t=115,52час/24*0,1сек/сутки = 0,48 сек=1,34*10-4 час.

Вставим полученные значения в формулу переноса ошибок:

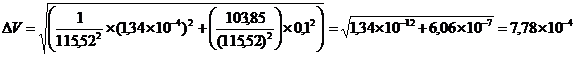мм/час

Ответ: Погрешность измерения скорости 4,78 10-4 мм/час.

5. Решение. Выпишем все единицы измерения, используемые для выражения характеристик продукции фирмы в разных странах. Для каждой единицы определим размерность и коэффициент пересчета в основную единицу для данной размерности. (В качестве основных единиц выберем единицы системы СИ). Для каждой страны определим список принятых в ней единиц измерения.

При вводе количественных значений, наша программа анализирует: в каких единицах они выражены и автоматически пересчитывает вводимое значение в основную единицу.

При вызове сайта программа спрашивает: житель какой страны интересуется его содержимым и автоматически настраивает вывод количественных характеристик в единицах измерения, принятых в данной стране.

Литература

1. Федеральный закон от 01.01.2001 г. N 184-ФЗ "О техническом регулировании". Собрание законодательства РФ, 30.12.2002, N 52 (ч. 1), ст. 5140

2. Федеральный закон от 01.01.2001 г. N 4871-I "Об обеспечении единства измерений" Ведомости Съезда народных депутатов Российской Федерации и Верховного Совета Российской Федерации от 01.01.01 г., N 23 ст. 811

3. "Статистические методы повышения качества". Пер с англ., М., "Финансы и статистика", 1990, 301 стр

[1] Парк технических средств – все приборы и механизмы, используемые на предприятии. Также, как и деревья парке, они требуют присмотра и ухаживания.

[2] Это одно из правил теории вероятностей

[3] Пример взят и книги Дэниела Бурстина «Американцы: национальный опыт». (М: Прогресс, 19с.)

[4] Например, размер кода операционной системы Windows XP составляем порядка 50 миллионов строк.

[5] Аккредитация – разрешение, выдаваемое органу на проведение сертификационной деятельности определенного вида (области аккредитации). Для получения аккредитации орган должен продемонстрировать свои возможности проведения сертификации (компетентность, материальную базу и т. д.)

[6] Система сертификации – официально оформленная система требований и правил проведения сертификации, которых придерживаются органы по сертификации, аккредитованные этой системой. Наиболее известная система сертификации в России: система ГОСТ Р, базовой организацией которой является ГОСТАНДАРТ РФ.

[7] В термине «защита от дурака» нет ничего обидного. Он появился в период Второй мировой войны. Снабжая армию США современным вооружением, специалисты столкнулись с проблемой. Плохо обученные солдаты ломали новую технику гораздо эффективнее, чем артиллерия противника. Для устранения этой беды были разработаны специальные методы, обеспечивающие сохранность техники при неверных действиях персонала.

[8] Очевидно, что чем чаще используются одни и те же модули, тем меньше будет общее число модулей, а значит, легче запрограммировать наш проект.

[9]Например, с помощью полигонов тестируются мощные офисные и графические пакеты, программы распознавания, электронного перевода и т. д.

[10] Вспомним увлекательную книжку Ж. Верна «Дети капитана Гранта». Героям пришлось совершить почти кругосветное путешествие из за отсутствия информации о долготе.

[11] Например, при регистрации программы как объекта интеллектуальной собственности оформление программной документации должно соответствовать требованиям стандартов 19.104-78 и 19.106-78.

[12] Депонирование – обеспечение сохранности какого либо объекта или документа.

[13] Арбитраж – специальный суд, разбирающий вопросы промышленного права

[14] Комплект документации по этой программе подготовили студентки группы ПВС 23 Баркова Наталья, Пугачева Светлана и Улдарова Кадрия

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8