Основы метрологии, стандартизации и сертификации (стр. 2 )

В нашем примере значение 99.99 встретилось 7 раз, 100,02 – 2 раза, а 100,05 ни разу.

Проделав достаточно большое число замеров, мы получим «горку». Изучив, таким образом, множество измерений совершенно различных величин, мы заметим, что форма «горки» (рис. 2.3) оказывается схожей для всех них. Впервые дал этому математическое объяснение немецкий математик Гаусс. Но прежде чем рассказывать о его исследованиях нам придется познакомиться с основными понятиями теории вероятности. Вы будете подробно изучать этот курс. Поэтому сейчас мы остановимся только на некоторых понятиях и фактах, нужных для понимания метрологии.

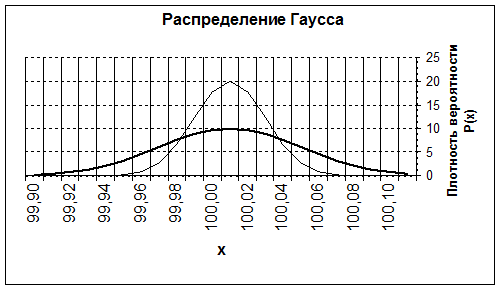
Рис. 2.3. Теоретические кривые Гаусса для различных распределений погрешности.

Назовем случайной величиной процесс, численную характеристику, которого нельзя предсказать заранее. Очевидно, многократное измерение одной величины является примером такого процесса. Частотой (Nm) появления определенного значения (m) случайной величины назовем количество случаев, в которых случайная величина принимает данное значение. В нашем примере частота значения 99,99 равна 7. Если мы предполагаем, что частоты появления различных значений отражают свойства самой случайной величины, желательно выразить эти свойства вне зависимости от числа испытаний (в нашем примере, замеров). Назовем вероятностью того, что случайная величина примет данное значение, предел отношения:

Pm= Lim (Nm/N) (4)

N→ ∞

Где Nm – частота появления значения m;

N – общее число испытаний.

Равенство полученного значения случайной величины определенному значению это событие в нашем вероятностном мире. Если события не зависят друг от друга, то вероятность появления какого - либо из них равна сумме их вероятностей[2]. Вероятность появления хоть какого-то события равна единице.

События, изображенные на рис. 2.З находятся так близко друг от друга, что их можно представить в виде непрерывной последовательности. Тогда кривую, похожую на шляпу гнома, можно интерпретировать как плотность вероятности, показывающую, насколько изменится вероятность события, если величина изменится на единицу.

Вероятность события X < X0 будет равна площади под кривой, от -∞ до линии X = X0 (рис. 2.4) .

Вероятность события X< 99,95 равна заштрихованной площади в левой части рисунка, вероятность X > 100,5 равна заштрихованной площади в правой части рисунка.

Вся площадь под кривой равна вероятности того, что Х примет хоть какое-то значение, т. е. равна единице. Тогда, вероятность того, что Х находится в интервале: X1<X<X2 равна единице минус заштрихованная площадь слева и справа. Выбрав X1 и X2 такими, чтобы заштрихованная площадь была небольшой (например, 0,01), мы можем сказать: «С доверительной вероятностью 1- 0,01= 0,99 величина X находится в интервале (X1; X2).

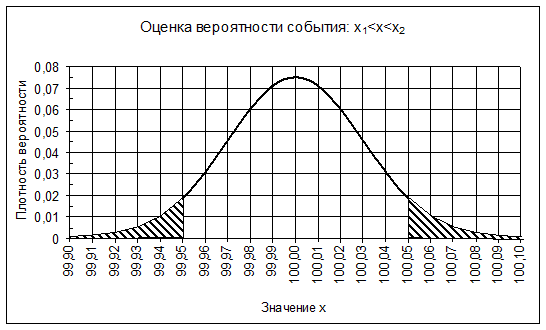Рис. 2.4. Оценка вероятности событий по графику функции плотности вероятности

Характеристики распределения случайной величины

Как видно из рис. 2.З, различные случайные величины имеют различный разброс своих значений. Наглядно это показывает различная ширина «шляп». В теории вероятности рассматриваются несколько характеристик случайных величин.

Среднее значение - предел отношения суммы всех значений к общему числу наблюдений:

(5)

Для оценки среднего значения используется допредельное выражение при достаточно большом числе испытаний N.

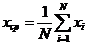(6)

Если случайная величина может принимать только определенные значения: X1 X2 Xm и известны вероятности появления этих значений P1 P2 Pm, среднее значение может быть вычислено по формуле:

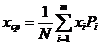(7)

Для оценки меры разброса случайной величины от её среднего значения подсчитаем сумму квадратов расстояний измеренных значений от среднего (рис 2.5)

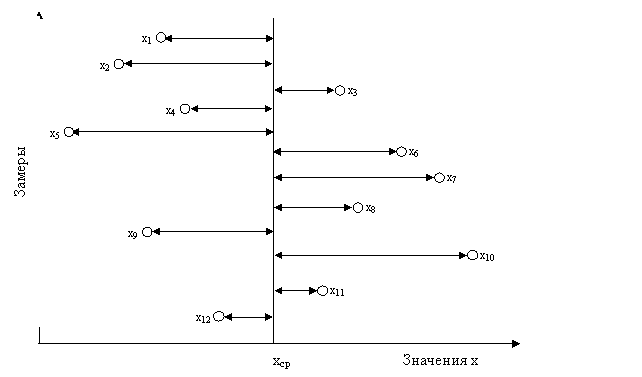
Рис. 2.5. Разброс измеряемых значений

Квадрат расстояния первого замера от среднего равен (х1-хср)2 . Для расчета среднего значения этой величины сложим все квадраты и поделим на число замеров.

Дисперсия – мера разброса значений случайной величины, определяется как среднее значение квадрата отклонения случайной величины от ее среднего значения:

(8)

Для оценки дисперсии при достаточно большом числе испытаний используется формула:

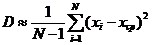(9)

Рассчитывать дисперсию по формуле (9) не очень удобно. Внесем знак суммы в скобки:

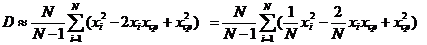(10)

и воспользуемся соотношениями:

Обозначим среднее значение квадрата случайной величины через :

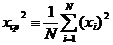
Подставив эти выражения в (10) получим формулу, удобную для вычисления дисперсии:

(11)

Отступление для программистов. Как организовать объемные вычисления?

Если бы мы запрограммировали вычисления дисперсии «в лоб» по формуле (9) нам бы пришлось организовать вложенные циклы: во внутреннем цикле считается , а во внешнем накапливается сумма 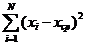. Пока наблюдений мало, ничего страшного не произойдет. А если их миллион? Даже на современных компьютерах такое вычисление займет десятки часов.

Немного подумав, мы можем организовать вычисления в два цикла: сначала один раз вычислим и запомним , а затем, во втором цикле будем считать сумму квадратов. Но и это не очень хорошо. Формула (11) позволяет вычислить нужные суммы за один цикл.

Из этого примера можно сделать вывод: Если Вам нужно выполнить какие то большие вычисления, не спешите писать код. Сначала подумайте над алгоритмом, выделите многократно используемые выражения и постарайтесь максимально упростить алгоритм.

Если случайная величина может принимать только определенные значения X1, X2, … XM с известными вероятностями P1. P2, …PM, дисперсия вычисляется по формуле:

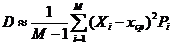(12)

Величина D характеризует разброс значений вокруг среднего. В случае измерений, D может использоваться в качестве меры случайной погрешности измерения. Однако, применение D не удобно. Дело в том, что размерность D равна квадрату размерности измеряемой величины. Например, мы измеряем расстояние в метрах. Подставим в (10) результаты наших замеров. Размерность D получилась равной м2. Поэтому вместо D, в качестве меры случайной ошибки, применяют величину σ – называемую среднеквадратическим отклонением.

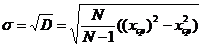(13)

Если случайная величина может принимать только М определенных значений с известными вероятностями, среднеквадратическое отклонение вычисляется по формуле:

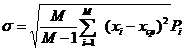(14)

Для распределения Гаусса справедливо соотношение: «Вероятность, того, что значение величины отличается от среднего значения более чем на 3σ меньше 0,01. Таким образом, мы можем использовать σ как меру погрешности нашего измерения.

Отступление для программистов. Как бороться с грубыми ошибками?

При организации ввода данных в нашу информационную систему мы можем использовать вероятностный метод выявления грубых ошибок в данных. Как мы видели, отклонения значения величины за 3σ маловероятны. Организуем ввод данных так, чтобы сразу считать Xср и σ для уже введенных данных. Тогда, при появлении значения отличающегося от среднего больше чем на 3σ, программа выдает сообщение: «Введенное значение маловероятно! Пожалуйста, проверьте правильность ввода». Вовсе не обязательно, что мы ошиблись. Но проверить стоит. Таким образом, компьютер обращает внимание оператора на маловероятную информацию, что позволяет сократить число грубых ошибок.

Что мы понимаем под погрешностью измерений

В таблице 2.3 сведены различные ситуации применения термина «погрешность измерения».

Таблица 2.3

Обратите внимание, что величины погрешности и доверительной вероятности взаимосвязаны: при увеличении доверительной вероятности растет доверительный интервал, а вместе с ним и погрешность. В общем случае роль доверительной вероятности играет характеристика «Достоверность результатов измерения». Поэтому, при описании измерения, необходимо указывать сразу пару характеристик: «Погрешность» и «Достоверность» измерения.

Способы представления погрешности

В зависимости от решаемых задач используются несколько способов представления погрешности:

·  Абсолютная погрешность – измеряется в тех же единицах что и измеряемая величина. Характеризует величину возможного отклонения истинного значения измеряемой величины от измеренного.

·  Относительная погрешность – отношение абсолютной погрешности к значению величины. Если мы хотим определить погрешность на всем интервале измерений, мы должны найти максимальное значение отношения на интервале. Измеряется в безразмерных единицах.

·  Класс точности – относительная погрешность, выраженная в процентах. Обычно значения класса точности выбираются из ряда: 0,1; 0,5: 1,0; 1,5; 2,0; 2,5 …

Косвенные измерения

При косвенных измерениях мы замеряем одну или несколько величин, которые мы умеем мерить, и по их значениям вычисляем искомую величину. Правило вычисления можно записать в виде формулы:

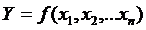(15)

Где Y – искомая величина,

x1,x2,…xn – величины, которые мы измеряем непосредственно,

f() – правило вычисления.

Как оценить погрешность Y если известны погрешности прямых измерений x1,x2,…xn? Сначала рассмотрим проблему в случае одной переменной. На рис. 2.5 приведен график зависимости Y от x. При изменении x на Δx величина Y меняется на ΔY. Если Δx мало (Δx << x), то значение ΔY мы можем найти с помощью производной f’(x):

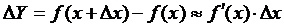
(16)

Истинное значение х может отличаться от измеренного и в большую и в меньшую сторону. Поэтому для определения ΔY нам придется взять не производную f’(x), а ее абсолютное значение |f’(x)|. Если мы хотим найти погрешность косвенного измерения на всем интервале измерений, заменим в формуле 13 величину f’(x) на ее максимальное значение в измеряемом интервале:

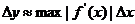(17)

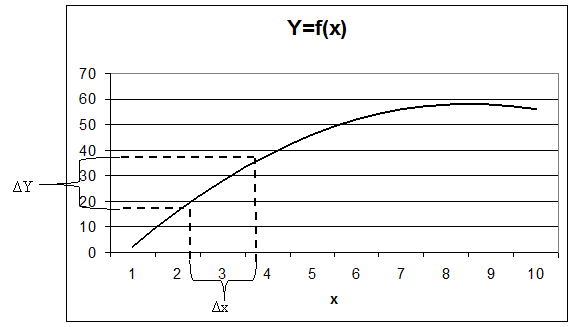
Рис. 2.5. Оценка погрешности косвенного измерения

В случае нескольких измерений, вместо производной можно было бы использовать частные производные по каждому xi:

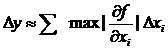(18)

Однако, формула (18) обладает одним неприятным свойством: при росте числа переменных доверительная вероятность быстро уменьшается.

Проиллюстрируем расчет доверительной вероятности для случая двух переменных. Пусть для каждого прямого измерения погрешность задана с доверительной вероятностью 0,95 (). Так как величины x1 и x2 независимы, вероятность совместного события:

(19)

Аналогично, для трех переменных, доверительная вероятность будет равна 0,953 =0,86, а для 10 переменных 0,9510≈0,6.

Чтобы избежать подобных проблем воспользуемся формулой дисперсии, переменные которой распределены по нормальному закону:

(20)

Среднеквадратическое отклонение функции, согласно (13) равняется:

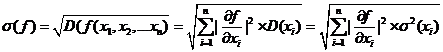(21)

Воспользуемся правилом трех сигм:

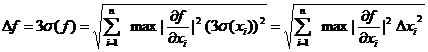(22)

Формула (22) называется правилом переноса ошибок. При некоторых ограничениях, на вид функции выполняющихся во многих практически важных случаях, распределение функции от нормально распределенных аргументов также можно считать нормальным. Следовательно, доверительная вероятность погрешности, рассчитанной по формуле (18) такая же, как и у прямых измерений xi.

Погрешность вычислений

Правило переноса ошибок позволяет оценить погрешность результата вычисления в зависимости от погрешности исходных данных. В качестве примера оценим погрешность многократного измерения. Окончательным результатом многократного измерения считается среднее значение всех замеров.

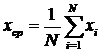(23)

Погрешность вычислим по правилу переноса ошибок:

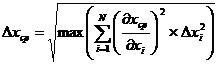(24)

Частные производные

(25)

Будем считать, что погрешности всех замеров одинаковы: . Вставим (25) в (24)

(26)

Таким образом, N замеров повышают точность измерения в раз. С ростом количества замеров точность растет, но вклад каждого нового замера снижается. Например, при девяти замерах точность вырастет в три раза, но для десятикратного увеличения точности потребуется сто замеров.

Рассмотрим еще один пример – погрешность произведения. 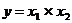. Найдем частные производные: и вставим их выражения в ().

(27)

Пусть сомножители заданы с 10% точностью: . Тогда погрешность произведения равна:

(28)

Таким образом, относительная погрешность произведения в раз больше, чем погрешности сомножителей. Если сомножителей не 2, а N, погрешность произведения больше погрешности сомножителей в раз

Как видно, чем сложнее вычисления, тем выше их погрешность.

Отступление для программистов. Избегайте ненужной сложности вычислений.

Чем сложнее вычисление, тем ниже его точность. Особенно это опасно при сложных итерационных вычислениях.

Поэтому, прежде чем писать код, продумайте и, по возможности, упростите алгоритм вычисления. Если упростить алгоритм не удается, для сокращения погрешности вычислений используйте переменные с двойной точностью.

Выборочный контроль

Мы хотим приобрести большую партию импортного растворимого кофе в 1 миллион банок. Если содержание кофеина в этом кофе превышает предельно допустимое значение, мы не сможем продавать эти банки на отечественном рынке. Чтобы определить значение этой характеристики в одной банке нужно ее вскрыть, взять пробу кофе и произвести замеры. А как быть с партией? Вскрыть все банки? Но, это очень долго и дорого. И что делать (как потом продавать) вскрытые банки?

При решении этой проблемы предположим, что все банки были изготовлены по единой технологии, скорее всего из одной партии сырья. Если такое предположение верно, мы можем вскрыть небольшое количество банок, измерить количество кофеина в их содержимом, усреднить и распространить (приписать) полученный результат на всю партию. Если содержание кофеина в проверенных банках ниже допустимого значения, будем считать, что вся партия прошла контроль и ее можно продавать на отечественном рынке. Такой метод называется выборочным контролем.

А как проверить само предположение об одинаковости характеристик в разных банках? На помощь нам приходят статистические методы. Сформулируем наше предположение в виде статистической гипотезы: «Характеристики всех единиц в данной партии продукции, в основном одинаковые. Небольшие различия обусловлены случайными отклонениями характеристик сырья и технологии производства». На языке статистики эта гипотеза выглядит так: «Величина X является суммой номинального значения X0 и случайной погрешности ε. Вероятность выхода погрешности из заданного интервала достаточно мала (например, меньше 5%)»

X = X0 + ε (23)

P( X<Xmin и X> Xmax) < 0,05

В статистике разработаны специальные методы проверки таких гипотез. Их основная идея проверить, удовлетворяют ли результаты контроля на выборке предположениям гипотезы. Если объем выборки достаточно большой (например, 100 банок), то статистические характеристики выборки (среднее значение, разброс значений и т. д.) должны приближаться к характеристикам генеральной совокупности (всей партии). Вычисляется вероятность наблюдаемых отклонений и если она приемлемо высокая, принимается основная гипотеза (об однородности партии). Если вероятность слишком мала, принимается альтернативная гипотеза: «Партия не однородна». В этом случае выборочный контроль применять нельзя.

Проверяя не все объекты, мы рискуем посчитать негодную партию годной, а годную негодной (рис. 2.6). Действительно, если при проверке «хорошей» партии нам случайно будут попадаться банки с повышенным содержанием кофеина, мы неправильно забракуем всю партию. При этом потери понесет поставщик, поэтому риск такого события называется: риск поставщика. Аналогично, если при проверке «плохой» партии случайно будут выбраны банки с приемлемым содержанием кофеина, вся партия пройдет контроль, а потребители могут получить потенциально опасный продукт. Риск такого события называется риск потребителя. Совокупность этих характеристик определяет достоверность контроля.

В зависимости от обстоятельств контроля, соотношение рисков поставщика и потребителя могут быть различными. Приведем два примера.

1) Контролируемый параметр определяет качество бытовой техники (например, суточный уход часов). Потребитель, купив часы, которые «убегают» за сутки больше, чем на положенные 0,1 сек, при желании, может обратиться в мастерскую и отрегулировать часы. Для обеспечения гарантированного значения ухода всех выпускаемых часов производителю необходимо сменить все оборудование и все технологии, что существенно повысит себестоимость и цену изделий. Риск потребителя существенно меньше риска поставщика.

2) Контролируемый параметр определяет безопасность изделия (например, электрическую безопасность бытовой техники). Использование потенциально опасной техники может привести к травмам и гибели человека. Поэтому сокращение риска потребителя существенно важнее некоторого повышения риска поставщика.

При организации выборочного контроля сопоставляются значимость рисков поставщика и потребителя, а также затраты на контроль. Находится оптимальное соотношение этих характеристик, на основе которого выбирается план контроля: объем и правило формирования выборки, критерии отнесения партии продукции к годной или негодной.

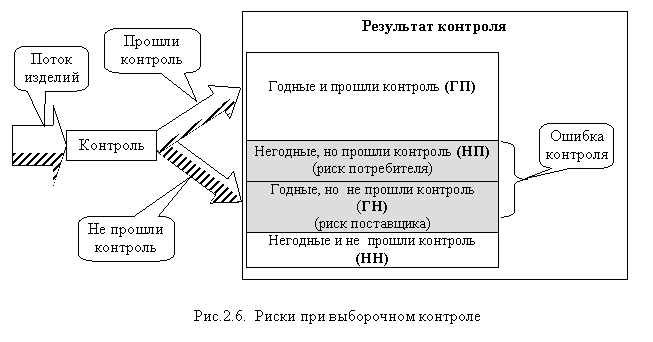
Таким образом, статистический контроль, как и любой другой контроль, имеет погрешность и достоверность. С увеличением объема выборки достоверность растет, а погрешность снижается. При равенстве объема выборки объему партии эти характеристики определяются только инструментальной погрешностью используемых приборов и достоверностью метода контроля. Т. е. при контроле всей партии характеристики выборочного контроля равны соответствующим характеристикам сплошного контроля.

Вопросы и задания

В таблице 2.4 приведены результаты измерения величины Х.

Таблица 2.4

№ замера	1	2	3	4	5	6	7	8
Результат	357,985	358,348	357,903	358,119	357,826	358,064	357,971	358,100
№ замера	9	10	11	12	13	14	15	16
Результат	358,224	358,155	357,733	358,189	357,808	358,046	357,896	357,984
№ замера	17	18	19	20	21	22	23	24
Результат	358,056	358,332	358,173	358,067	358,080	357,900	357,947	357,991

Оцените значение измеряемой величины и погрешность измерения для доверительной вероятности 99%

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8