Часть I ТЕОРИЯ
Глава 1
ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
Под нейронными сетями подразумеваются вычислительные структуры, которые моделируют простые биологические процессы, обычно ассоциируемые с процессами человеческого мозга. Они представляют собой распределенные и параллельные системы, способные к адаптивному обучению путем анализа положительных и отрицательных воздействий. Элементарным преобразователем в данных сетях является искусственный нейрон или просто нейрон, названный так по аналогии с биологическим прототипом.
К настоящему времени предложено и изучено большое количество моделей нейроподобных элементов и нейронных сетей, ряд из которых рассмотрен в настоящей главе.
1.1. Биологический нейрон
Нервная система и мозг человека состоят из нейронов, соединенных между собой нервными волокнами. Нервные волокна способны передавать электрические импульсы между нейронами. Все процессы передачи раздражений от кожи, ушей и глаз к мозгу, процессы мышления и управления действиями - все это реализовано в живом организме как передача электрических импульсов между нейронами.
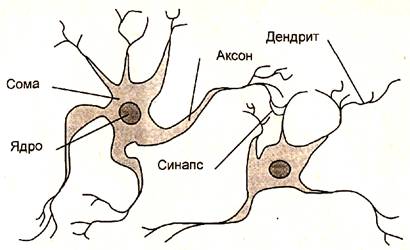 |
Рис. 1.1. Взаимосвязь биологических нейронов
Нейрон (нервная клетка) является особой биологической клеткой, которая обрабатывает информацию (рис. 1.1). Он состоит из тела (cell body), или сомы (soma), и отростков нервных волокон двух типов - дендритов (dendrites), по которым принимаются импульсы, и единственного аксона (ахоn), по которому нейрон может передавать импульс. Тело нейрона включает ядро (nucleus), которое содержит информацию о наследственных свойствах, и плазму, обладающую молекулярными средствами для производства необходимых нейрону материалов. Нейрон получает сигналы (импульсы) от аксонов других нейронов через дендриты (приемники) и передает сигналы, сгенерированные телом клетки, вдоль своего аксона (передатчика), который в конце разветвляется на волокна (strands). На окончаниях этих волокон находятся специальные образования - синапсы (synapses), которые влияют на величину импульсов.
Синапс является элементарной структурой и функциональным узлом между двумя нейронами (волокно аксона одного нейрона и дендрит другого). Когда импульс достигает синаптического окончания, высвобождаются химические вещества, называемые нейротрансмиттерами. Нейротрансмиттеры диффундируют через синаптическую щель, возбуждая или затормаживая, в зависимости от типа синапса, способность нейрона-приемника генерировать электрические импульсы. Результативность передачи импульса синапсом может настраиваться проходящими через него сигналами так, что синапсы могут обучаться в зависимости от активности процессов, в которых они участвуют. Эта зависимость от предыстории действует как память, которая, возможно, ответственна за память человека. Важно отметить, что веса синапсов могут изменяться со временем, а значит, меняется и поведение соответствующих нейронов.
Кора головного мозга человека содержит около 1011 нейронов и представляет собой протяженную поверхность толщиной от 2 до 3 мм с площадью около 2200 см2. Каждый нейрон связан с 103-104 другими нейронами. В целом мозг человека содержит приблизительно от 1014 до 1015 взаимосвязей.
Нейроны взаимодействуют короткими сериями импульсов продолжительностью, как правило, несколько миллисекунд. Сообщение передается посредством частотно-импульсной модуляции. Частота может изменяться от нескольких единиц до сотен герц, что в миллион раз медленнее, чем быстродействующие переключательные электронные схемы. Тем не менее сложные задачи распознавания человек решает за несколько сотен миллисекунд. Эти решения контролируются сетью нейронов, которые имеют скорость выполнения операций всего несколько миллисекунд. Это означает, что вычисления требуют не более 100 последовательных стадий. Другими словами, для таких сложных задач мозг «запускает» параллельные программы, содержащие около 100 шагов. Рассуждая аналогичным образом, можно обнаружить, что количество информации, посылаемое от одного нейрона другому, должно быть очень малым (несколько бит). Отсюда следует, что основная информация не передается непосредственно, а захватывается и распределяется в связях между нейронами.
1.2. Структура и свойства искусственного нейрона
Нейрон является составной частью нейронной сети. На рис. 1.2 показана его структура. Он состоит из элементов трех типов: умножителей (синапсов), сумматора и нелинейного преобразователя. Синапсы осуществляют связь между нейронами, умножают входной сигнал на число, характеризующее силу связи, (вес синапса). Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента - выхода сумматора. Эта функция называется функцией активации или передаточной функцией нейрона. Нейрон в целом реализует скалярную функцию векторного аргумента. Математическая модель нейрона:
где wi - вес(weight)синапса, i = 1...n;b - значение смещения (bias); s - результат суммирования (sum); хi - компонент входного вектора (входной сигнал), i = 1...n; у - выходной сигнал нейрона; n - число входов нейрона; f - нелинейное преобразование (функция активации).
В общем случае входной сигнал, весовые коэффициенты и смещение могут принимать действительные значения, а во многих практических задачах - лишь некоторые фиксированные значения. Выход (у) определяется видом функции активации и может быть как действительным, так и целым.
Синаптические связи с положительными весами называют возбуждающими, с отрицательными весами - тормозящими.
Описанный вычислительный элемент можно считать упрощенной математической моделью биологических нейронов. Чтобы подчеркнуть различие нейронов биологических и искусственных, вторые иногда называют нейроноподобными элементами или формальными нейронами.
На входной сигнал (s) нелинейный преобразователь отвечает выходным сигналом f(s), который представляет собой выход у нейрона. Примеры активационных функций представлены в табл. 1.1 и на рис. 1.3.
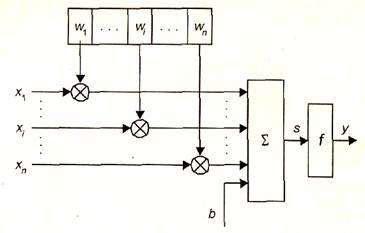 |
Рис. 1.2. Структура искусственного нейрона
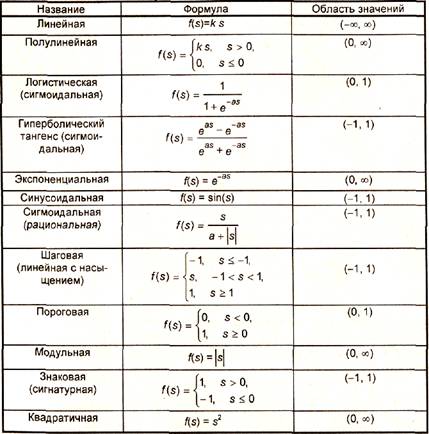 |
Таблица 1.1
Функции активации нейронов
Одной из наиболее распространенных является нелинейная функция активации с насыщением, так называемая логистическая функция или сигмоид (функция S-образного вида):
При уменьшении а сигмоид становится более пологим, в пределе при а = 0 вырождаясь в горизонтальную линию на уровне 0,5, при увеличении а сигмоид приближается к виду функции единичного скачка с порогом θ. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне (0, 1). Одно из ценных свойств сигмоидальнои функции - простое выражение для ее производной, применение которой будет рассмотрено в дальнейшем:
Следует отметить, что сигмоидальная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Кроме того, она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон.
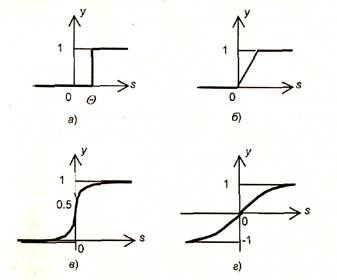 |
Рис. 1.3. Примеры активационных функций:
а - функция единичного скачка; б - линейный порог (гистерезис); в - сигмоид (логистическая функция); г - сигмоид (гиперболический тангенс)
1.3. Классификация нейронных сетей и их свойства
Нейронная сеть представляет собой совокупность нейроподобных элементов, определенным образом соединенных друг с другом и с внешней средой с помощью связей, определяемых весовыми коэффициентами. В зависимости от функций, выполняемых нейронами в сети, можно выделить три их типа:
• входные нейроны, на которые подается вектор, кодирующий входное воздействие или образ внешней среды; в них обычно
не осуществляется вычислительных процедур, а информация передается с входа на выход путем изменения их активации;
• выходные нейроны, выходные значения которых представляют выходы нейронной сети; преобразования в них осуществляются по выражениям (1.1) и (1.2);
• промежуточные нейроны, составляющие основу нейронных сетей, преобразования в которых выполняются также по выражениям (1.1) и (1.2).
В большинстве нейронных моделей тип нейрона связан с его расположением в сети. Если нейрон имеет только выходные связи, то это входной нейрон, если наоборот - выходной нейрон. Однако возможен случай, когда выход топологически внутреннего нейрона рассматривается как часть выхода сети. В процессе функционирования сети осуществляется преобразование входного вектора в выходной, некоторая переработка информации. Конкретный вид выполняемого сетью преобразования данных обусловливается не только характеристиками нейроподобных элементов, но и особенностями ее архитектуры, а именно топологией межнейронных связей, выбором определенных подмножеств нейроподобных элементов для ввода и вывода информации, способами обучения сети, наличием или отсутствием конкуренции между нейронами, направлением и способами управления и синхронизации передачи информации между нейронами.
С точки зрения топологии можно выделить три основных типа нейронных сетей:
• полносвязные (рис. 1.4, а);
• многослойные или слоистые (рис. 1.4, б);
• слабосвязные (с локальными связями) (рис. 1.4, в).
В полносвязных нейронных сетях каждый нейрон передает свой выходной сигнал остальным нейронам, в том числе и самому себе. Все входные сигналы подаются всем нейронам. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети,
В многослойных нейронных сетях нейроны объединяются в слои. Слой содержит совокупность нейронов с едиными входными сигналами. Число нейронов в слое может быть любым и не зависит от количества нейронов в других слоях. В общем случае сеть состоит из Q слоев, пронумерованных слева направо. Внешние входные сигналы подаются на входы нейронов входного слоя (его часто нумеруют как нулевой), а выходами сети являются выходные сигналы последнего слоя. Кроме входного и выходного слоев в многослойной нейронной сети есть один или несколько скрытых слоев. Связи от выходов нейронов некоторого слоя q к входам нейронов следующего слоя (q+1) называются последовательными.
в)
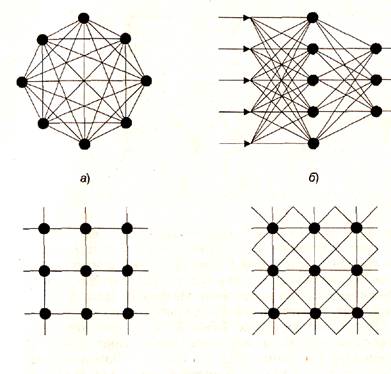 |
Рис. 1.4. Архитектуры нейронных сетей:
а - полносвязная сеть, б - многослойная сеть с последовательными связями, в - слабосвязные сети
В свою очередь, среди многослойных нейронных сетей выделяют следующие типы.
1) Монотонные,
Это частный случай слоистых сетей с дополнительными условиями на связи и нейроны. Каждый слой кроме последнего (выходного) разбит на два блока: возбуждающий и тормозящий. Связи между блоками тоже разделяются на тормозящие и возбуждающие. Если от нейронов блока А к нейронам блока В ведут только возбуждающие связи, то это означает, что любой выходной сигнал блока является монотонной неубывающей функцией любого выходного сигнала блока А. Если же эти связи только тормозящие, то любой выходной сигнал блока В является невозрастающей функцией любого выходного сигнала блока А. Для нейронов монотонных сетей необходима монотонная зависимость выходного сигнала нейрона от параметров входных сигналов.
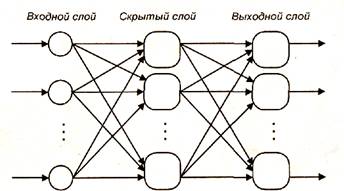 |
Рис. 1.5. Многослойная (двухслойная) сеть прямого распространения
2) Сети без обратных связей. В таких сетях нейроны входного слоя получают входные сигналы, преобразуют их и передают
нейронам первого скрытого слоя, и так далее вплоть до выходного,
который выдает сигналы для интерпретатора и пользователя. Если не оговорено противное, то каждый выходной сигнал q-гo слоя
подастся на вход всех нейронов (q+1)-го слоя; однако возможен
вариант соединения q-го слоя с произвольным (q+ p )-м слоем.
Среди многослойных сетей без обратных связей различают полносвязанные (выход каждого нейрона q-гo слоя связан с входом каждого нейрона (q+1)-го слоя) и частично полносвязанные. Классическим вариантом слоистых сетей являются полносвязанные сети прямого распространения (рис. 1.5).
3) Сети с обратными связями. В сетях с обратными связями информация с последующих слоев передается на предыдущие.
Среди них, в свою очередь, выделяют следующие:
• слоисто-циклические, отличающиеся тем, что слои замкнуты в кольцо: последний слой передает свои выходные сигналы первому; все слои равноправны и могут как получать входные сигналы, так и выдавать выходные;
• слоисто-полносвязанные состоят из слоев, каждый из которых представляет собой полносвязную сеть, а сигналы передаются как от слоя к слою, так и внутри слоя; в каждом слое цикл работы распадается на три части: прием сигналов с предыдущего слоя, обмен сигналами внутри слоя, выработка выходного сигнала и передача к последующему слою;
• полносвязанно-слоистые, по своей структуре аналогичные слоисто-полносвязанным, но функционирующим по-другому: в них не разделяются фазы обмена внутри слоя и передачи следующему, на каждом такте нейроны всех слоев принимают сигналы от нейронов как своего слоя, так и последующих.
В качестве примера сетей с обратными связями на рис. 1.6 представлены частично-рекуррентные сети Элмана и Жордана.
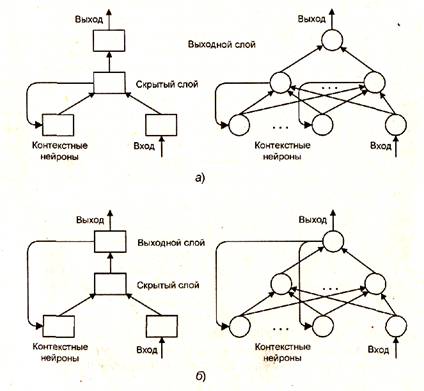 |
Рис. 1.6. Частично-рекуррентные сети: а - Элмана, б - Жордана
В слабосвязных нейронных сетях нейроны располагаются в узлах прямоугольной или гексагональной решетки. Каждый нейрон связан с четырьмя {окрестность фон Неймана), шестью (окрестность Голея) или восемью (окрестность Мура) своими ближайшими соседями.
Известные нейронные сети можно разделить по типам структур нейронов на гомогенные (однородные) и гетерогенные. Гомогенные сети состоят из нейронов одного типа с единой функцией активации, а в гетерогенную сеть входят нейроны с различными функциями активации.
Существуют бинарные и аналоговые сети. Первые из них оперируют только двоичными сигналами, и выход каждого нейрона может принимать значение либо логического ноля (заторможенное состояние) либо логической единицы (возбужденное состояние).
Еще одна классификация делит нейронные сети на синхронные и асинхронные. В первом случае в каждый момент времени лишь один нейрон меняет свое состояние, во втором - состояние меняется сразу у целой группы нейронов, как правило, у всего слоя. Алгоритмически ход времени в нейронных сетях задается итерационным выполнением однотипных действий над нейронами. Далее будут рассматриваться только синхронные сети.
Сети можно классифицировать также по числу слоев. Теоретически число слоев и число нейронов в каждом слое может быть произвольным, однако фактически оно ограничено ресурсами компьютера или специализированных микросхем, на которых обычно реализуется нейронная сеть. Чем сложнее сеть, тем более сложные задачи она может решать.
Выбор структуры нейронной сети осуществляется в соответствии с особенностями и сложностью задачи. Для решения отдельных типов задач уже существуют оптимальные конфигурации, описанные в приложении. Если же задача не может быть сведена ни к одному из известных типов, приходится решать сложную проблему синтеза новой конфигурации. При этом необходимо руководствоваться следующими основными правилами:
• возможности сети возрастают с увеличением числа нейронов сети, плотности связей между ними и числом слоев;
• введение обратных связей наряду с увеличением возможностей сети поднимает вопрос о динамической устойчивости сети;
• сложность алгоритмов функционирования сети, введение нескольких типов синапсов способствует усилению мощности нейронной сети.
Вопрос о необходимых и достаточных свойствах сети для решения задач того или иного рода представляет собой целое направление нейрокомпьютерной науки. Так как проблема синтеза нейронной сети сильно зависит от решаемой задачи, дать общие подробные рекомендации затруднительно. В большинстве случаев оптимальный вариант получается на основе интуитивного подбора, хотя в литературе приведены доказательства того, что для любого алгоритма существует нейронная сеть, которая может его реализовать. Остановимся на этом подробнее.
Многие задачи распознавания образов (зрительных, речевых), выполнения функциональных преобразований при обработке сигналов, управления, прогнозирования, идентификации сложных систем, сводятся к следующей математической постановке. Необходимо построить такое отображение X -> У, чтобы на каждый возможный входной сигнал X формировался правильный выходной сигнал Y. Отображение задается конечным набором пар (<вход>, <известный выход>). Число этих пар (обучающих примеров) существенно меньше общего числа возможных сочетаний значений входных и выходных сигналов. Совокупность всех обучающих примеров носит название обучающей выборки.
В задачах распознавания образов X - некоторое представление образа (изображение, вектор), У - номер класса, к которому принадлежит входной образ.
В задачах управления X - набор контролируемых параметров управляемого объекта, У - код, определяющий управляющее воздействие, соответствующее текущим значениям контролируемых параметров.
В задачах прогнозирования в качестве входных сигналов используются временные ряды, представляющие значения контролируемых переменных на некотором интервале времени. Выходной сигнал - множество переменных, которое является подмножеством переменных входного сигнала.
При идентификации X и У представляют входные и выходные сигналы системы соответственно.
Вообще говоря, большая часть прикладных задач может быть сведена к реализации некоторого сложного функционального многомерного преобразования.
В результате отображения X -> У необходимо обеспечить формирование правильных выходных сигналов в соответствии:
• со всеми примерами обучающей выборки;
• со всеми возможными входными сигналами, которые не
вошли в обучающую выборку.
Второе требование в значительной степени усложняет задачу формирования обучающей выборки. В общем виде эта задача в настоящее время еще не решена, однако во всех известных случаях может быть найдено частное решение.
1.3.1. Теорема Колмогорова-Арнольда
Построить многомерное отображение X -> У - это значит представить его с помощью математических операций над не более, чем двумя переменными.
Проблема представления функций многих переменных в виде суперпозиции функций меньшего числа переменных восходит 13-й проблеме Гильберта. В результате многолетней научной полемики между и был получен ряд важных теоретических результатов, опровергающих тезис непредставимости функции многих переменных функциями меньшего числа переменных:
• теорема о возможности представления непрерывных функций нескольких переменных суперпозициями непрерывных функций меньшего числа переменных (1956 г.);
• теорема о представлении любой непрерывной функции трех переменных в виде суммы функций не более двух переменных (1957 г.);
• теорема о представлении непрерывных функций нескольких переменных в виде суперпозиций непрерывных функций одного переменного и сложения (1957 г.).
1.3.2. Работа Хехт-Нильсена
Теорема о представлении непрерывных функций нескольких переменных в виде суперпозиций непрерывных функций одного переменного и сложения в 1987 году была переложена Хехт-Нильсеном для нейронных сетей.
Теорема Хехт-Нильсена доказывает представимость функции многих переменных достаточно общего вида с помощью двухслойной нейронной сети с прямыми полными связями с n нейронами входного слоя, (2n+1) нейронами скрытого слоя с заранее известными ограниченными функциями активации (например, сигмоидальными) и т нейронами выходного слоя с неизвестными функциями активации.
Теорема, таким образом, в неконструктивной форме доказывает решаемость задачи представления функции произвольного вида на нейронной сети и указывает для каждой задачи минимальные числа нейронов сети, необходимых для ее решения.
1.3.3. Следствия из теоремы Колмогорова-Арнольда - Хехт-Нильсена
Следствие 1. Из теоремы Хехт-Нильсена следует представимость любой многомерной функции нескольких переменных с помощью нейронной сети фиксированной размерности. Неизвестными остаются следующие характеристики функций активации нейронов:
• ограничения области значений (координаты асимптот) сигмоидальных функций активации нейронов скрытого слоя;
• наклон сигмоидальных функций активации;
• вид функций активации нейронов выходного слоя.
Про функции активации нейронов выходного слоя из теоремы Хехт-Нильсена известно только то, что они представляют собой нелинейные функции общего вида. В одной из работ, продолжающих развитие теории, связанной с рассматриваемой теоремой, доказывается, что функции активации нейронов выходного слоя должны быть монотонно возрастающими. Это утверждение в некоторой степени сужает класс функций, которые могут использоваться при реализации отображения с помощью двухслойной нейронной сети.
На практике требования теоремы Хехт-Нильсена к функциям активации удовлетворяются следующим образом. В нейронных сетях как для первого (скрытого), так и для второго (выходного) слоя используют сигмоидальные передаточные функции с настраиваемыми параметрами. То есть в процессе обучения индивидуально для каждого нейрона задается максимальное и минимальное значение, а также наклон сигмоидальной функции.
Следствие 2. Для любого множества пар (Xk, Vk) (где Уk - скаляр) существует двухслойная однородная (с одинаковыми функциями активации) нейронная сеть первого порядка с последовательными связями и с конечным числом нейронов, которая выполняет отображение X -> У, выдавая на каждый входной сигнал У правильный выходной сигнал Уk. Нейроны в такой двухслойной нейронной сети должны иметь сигмоидальные передаточные функции.
К сожалению, эта теорема не конструктивна. В ней не заложена методика определения числа нейронов в сети для некоторой конкретной обучающей выборки.
Для многих задач единичной размерности выходного сигнала недостаточно. Необходимо иметь возможность строить с помощью нейронных сетей функции X -> У, где У имеет произвольную размерность. Следующее утверждение является теоретической основой для построения таких функций на базе однородных нейронных сетей.
Утверждение. Для любого множества пар входных-выходных векторов произвольной размерности {(Xk, Yk ), k = 1...N} существует однородная двухслойная нейронная сеть с последовательными связями, с сигмоидальными передаточными функциями и с конечным числом нейронов, которая для каждого входного вектора У формирует соответствующий ему выходной вектор Vk.
Таким образом, для представления многомерных функций многих переменных может быть использована однородная двухслойная нейронная сеть с сигмоидальными передаточными функциями.
Для оценки числа нейронов с скрытых слоях однородных нейронных сетей можно воспользоваться формулой для оценки необходимого числа синаптических весов Lw в многослойной сети с сигмоидальными передаточными функциями:
где п - размерность входного сигнала, т - размерность выходного сигнала, N - число элементов обучающей выборки.
Оценив необходимое число весов, можно рассчитать число нейронов в скрытых слоях. Например, для двухслойной сети это число составит:
Известны и другие формулы для оценки, например:
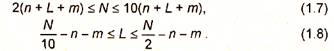 |
Точно так же можно рассчитать число нейронов в сетях с большим числом слоев.
Иногда целесообразно использовать сети с большим числом слоев. Такие многослойные нейронные сети могут иметь меньшие размерности матриц синаптических весов нейронов одного слоя, чем двухслойные сети, реализующие то же самое отображение. Однако строгой методики построения таких сетей пока нет.
Аналогичная ситуация складывается и с многослойными нейронными сетями. В которых помимо последовательных связей используются и прямые (связи от слоя с номером q к слою с номером (q+p), где p>1). Нет строгой теории, которая показала бы возможность и целесообразность построения таких сетей.
Наибольшие проблемы возникают при использовании сетей циклического функционирования. К этой группе относятся многослойные сети с обратными связями (от слоя с номером q к слою с номером (q+p), где р < 0), а также полносвязные сети. Для успешного функционирования таких сетей необходимо соблюдение условий динамической устойчивости, иначе сеть может не сойтись к правильному решению, либо, достигнув на некоторой итерации правильного значения выходного сигнала, после нескольких итераций уйти от этого значения. Проблема динамической устойчивости подробно исследована, пожалуй, лишь для одной модели из рассматриваемой группы - нейронной сети Хопфилда.
Отсутствие строгой теории для перечисленных моделей нейронных сетей не препятствует исследованию возможностей их применения.
Отметим, что отечественному читателю приведенные результаты известны в более фрагментарной форме - в виде так называемой теоремы о полноте.
Теорема о полноте.
Любая непрерывная функция на замкнутом ограниченном множестве может быть равномерно приближена функциями, вычисляемыми нейронными сетями, если функция активации нейрона дважды непрерывно дифференцируема и непрерывна.
Таким образом, нейронные сети являются универсальными структурами, позволяющими реализовать любой вычислительный алгоритм.
1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
Очевидно, что процесс функционирования нейронной сети, сущность действий, которые она способна выполнять, зависит от величин синаптических связей. Поэтому, задавшись определенной структурой сети, соответствующей какой-либо задаче, необходимо найти оптимальные значения всех переменных весовых коэффициентов (некоторые синаптические связи могут быть постоянными).
Этот этап называется обучением нейронной сети, и от того, насколько качественно он будет выполнен, зависит способность сети решать поставленные перед ней проблемы во время функционирования.
В процессе функционирования нейронная сеть формирует выходной сигнал У в соответствии с входным сигналом X, реализуя некоторую функцию g: Y = g(Х). Если архитектура сети задана, то вид функции g определяется значениями синаптических весов и смещений сети. Обозначим через G множество всех возможных функций g, соответствующих заданной архитектуре сети.
Пусть решение некоторой задачи есть функция r. У = r(Х), заданная парами входных - выходных данных (X1, У1), ..., (Xk, Уk), для которых Уk= r(Xk), k= 1...N. Е-функция ошибки (функционал качества), показывающая для каждой из функций g степень близости к r.
Решить поставленную задачу с помощью нейронной сети заданной архитектуры - это значит построить (синтезировать) функцию g € G, подобрав параметры нейронов (синаптические веса и смещения) таким образом, чтобы функционал качества обращался в оптимум для всех пар (Xk, Yk).
Таким образом, задача обучения нейронной сети определяется совокупностью пяти компонентов:
<Х, У, r, G, Е>.
Обучение состоит в поиске (синтезе) функции g, оптимальной по Е. Оно требует длительных вычислений и представляет собой итерационную процедуру. Число итераций может составлять от 103 до 108. На каждой итерации происходит уменьшение функции ошибки.
Функция Е может иметь произвольный вид. Если выбраны множество обучающих примеров и способ вычисления функции ошибки, обучение нейронной сети превращается в задачу многомерной оптимизации, для решения которой могут быть использованы следующие методы:
• локальной оптимизации с вычислением частных производных первого порядка;
• локальной оптимизации с вычислением частных производных первого и второго порядка;
• стохастической оптимизации;
• глобальной оптимизации.
К первой группе относятся: градиентный метод (наискорейшего спуска); методы с одномерной и двумерной оптимизацией целевой функции в направлении антиградиента; метод сопряженных градиентов; методы, учитывающие направление антиградиента на нескольких шагах алгоритма.
Ко второй группе относятся: метод Ньютона, методы оптимизации с разреженными матрицами Гессе, квазиньютоновские методы, метод Гаусса-Ньютона, метод Левенберга-Маркардта.
Стохастическими методами являются: поиск в случайном направлении, имитация отжига, метод Монте-Карло (численный метод статистических испытаний).
Задачи глобальной оптимизации решаются с помощью перебора значений переменных, от которых зависит целевая функция.
Для сравнения методов обучения нейронных сетей необходимо использовать два критерия:
• количество шагов алгоритма для получения решения;
• количество дополнительных переменных для организации вычислительного процесса.
Для иллюстрации термина «дополнительные переменные» приведем следующий пример. Пусть р1 и р2 - некоторые параметры нейронной сети с заданными значениями. В процессе обучения сети на каждом шаге, по меньшей мере, два раза потребуется выполнить умножение p1p2. Дополнительная переменная требуется для сохранения значение произведения после первого умножения.
Предпочтение следует отдавать тем методам, которые позволяют обучить нейронную сеть за небольшое число шагов и требуют малого числа дополнительных переменных. Это связано с ограничением ресурсов вычислительных средств. Как правило, для обучения используются персональные компьютеры.
Пусть нейронная сеть содержит Р изменяемых параметров (синаптических весов и смещений). Существует лишь две группы алгоритмов обучения, которые требуют менее 2Р дополнительных параметров и при этом дают возможность обучать нейронные сети за приемлемое число шагов. Это алгоритмы с вычислением частных производных первого порядка и, возможно, одномерной оптимизации. Именно эти алгоритмы и будут рассмотрены в следующих разделах.
Хотя указанные алгоритмы дают возможность находить только локальные экстремумы, они могут быть использованы на практике для обучения нейронных сетей с многоэкстремальными целевыми функциями (функциями ошибки), так как экстремумов у целевой функции, как правило, не очень много. Достаточно лишь раз или два вывести сеть из локального минимума с большим значением целевой функции для того, чтобы в результате итераций в соответствии с алгоритмом локальной оптимизации сеть оказалась в локальном минимуме со значением целевой функции, близким к нулю. Если после нескольких попыток вывести сеть из локального минимума нужного эффекта добиться не удается, необходимо увеличить число нейронов во всех слоях с первого по предпоследний и присвоить случайным образом их синаптическим весам и смещениям значения из заданного диапазона.
Эксперименты по обучению нейронных сетей показали, что совместное использование алгоритма локальной оптимизации, процедуры вывода сети из локального минимума и процедуры увеличения числа нейронов приводит к успешному обучению нейронных сетей.
Кратко опишем недостатки других методов. Стохастические алгоритмы требуют очень большого числа шагов обучения. Это делает невозможным их практическое использование для обучения нейронных сетей больших размерностей. Экспоненциальный рост сложности перебора с ростом размерности задачи в алгоритмах глобальной оптимизации при отсутствии априорной информации о характере целевой функции также делает невозможным их использование для обучения нейронных сетей больших размерностей. Метод сопряженных градиентов очень чувствителен к точности вычислений, особенно при решении задач оптимизации большой размерности. Для методов, учитывающих направление антиградиента на нескольких шагах алгоритма, и методов, включающих вычисление матрицы Гессе, необходимо более чем 2Р дополнительных переменных. В зависимости от способа разрежения, вычисление матрицы Гессе требует от 2Р до Р2 дополнительных переменных.
Рассмотрим один из самых распространенных алгоритмов обучения - алгоритм обратного распространения ошибки.
1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
В многослойных нейронных сетях оптимальные выходные значения нейронов всех слоев, кроме последнего, как правило, неизвестны. Трех- или более слойный персептрон уже невозможно обучить, руководствуясь только величинами ошибок на выходах сети.
Один из вариантов решения этой проблемы - разработка наборов выходных сигналов, соответствующих входным, для каждого слоя нейронной сети, что, конечно, является очень трудоемкой операцией и не всегда осуществимо. Второй вариант - динамическая подстройка весовых коэффициентов синапсов, в ходе которой выбираются, как правило, наиболее слабые связи и изменяются на малую величину в ту или иную сторону, а сохраняются только те изменения, которые повлекли уменьшение ошибки на выходе всей сети. Очевидно, что данный метод, несмотря на кажущуюся простоту, требует громоздких рутинных вычислений. И, наконец, третий, более приемлемый вариант - распространение сигналов ошибки от выходов нейронной сети к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Этот алгоритм обучения получил название процедуры обратного распространения ошибки (error back propagation). Именно он рассматривается ниже.
Алгоритм обратного распространения ошибки - это итеративный градиентный алгоритм обучения, который используется с целью минимизации среднеквадратичного отклонения текущих от требуемых выходов многослойных нейронных сетей с последовательными связями.
Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки нейронной сети является величина:
где yj, k(Q) - реальное выходное состояние нейрона j выходного слоя
нейронной сети при подаче на ее входы k-гo образа; dj,k - требуемое выходное состояние этого нейрона.
Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация методом градиентного спуска обеспечивает подстройку весовых коэффициентов следующим образом:
где Wij - весовой коэффициент синаптической связи, соединяющей i-й нейрон слоя (q -1) с j-м нейроном слоя q; η - коэффициент скорости обучения, 0 < η<1.
В соответствии с правилом дифференцирования сложной функции:
где Sj - взвешенная сумма входных сигналов нейрона j, т. е. аргумент активационной функции. Так как производная активационной функции должна быть определена на всей оси абсцисс, то функция единичного скачка и прочие активационные функции с неоднородностями не подходят для рассматриваемых нейронных сетей. В них применяются такие гладкие функции, как гиперболический тангенс или классический сигмоид с экспонентой (см. табл. 1.1). Например, в случае гиперболического тангенса:
Третий множитель ∂sj /∂Wij равен выходу нейрона предыдущего слоя уi(q-1).
Что касается первого множителя в (1.11), он легко раскладывается следующим образом:
Здесь суммирование по r выполняется среди нейронов слоя (q+1). Введя новую переменную:
Для выходного слоя:
Теперь можно записать (1.10) в раскрытом виде:
Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки при перемещении по поверхности целевой функции, (1.17) дополняется значением изменения веса на предыдущей итерации:
где µ- коэффициент инерционности; t - номер текущей итерации.
Таким образом, полный алгоритм обучения нейронной сети с помощью процедуры обратного распространения строится следующим образом.
ШАГ 1. Подать на входы сети один из возможных образов и в режиме обычного функционирования нейронной сети, когда сигналы распространяются от входов к выходам, рассчитать значения последних. Напомним, что:
где L - число нейронов в слое (q -1) с учетом нейрона с постоянным выходным состоянием +1, задающего смещение; уi(q-1) wij(q) – i-й вход нейрона j слоя q,
уi(q) = f(sj(q) ), (1.20)
где f( •) - сигмоид,
уr(о) = хr, (1.21)
где хr - r-я компонента вектора входного образа.
ШАГ 2. Рассчитать δ(Q) для выходного слоя по формуле (1.16).
Рассчитать по формуле (1.17) или (1.18) изменения весов Δw(Q) слоя Q.
ШАГ 3. Рассчитать по формулам (1.15) и (1.17) (или (1.15) и (1.18)) соответственно δ(q) и Δw(Q) для всех остальных слоев, q = (Q-1)...1.
ШАГ 4. Скорректировать все веса в нейронной сети:
wij(q)(t)= wij(q)w(t-1) + ∆wij(q)w(t) (1.22)
ШАГ 5. Если ошибка сети существенна, перейти на шаг 1. В противном случае - конец.
Сети на шаге 1 попеременно в случайном порядке предъявляются все тренировочные образы, чтобы сеть, образно говоря, не забывала одни по мере запоминания других.
Из выражения (1.17) следует, что когда выходное значение уi(q-1) стремится к нулю, эффективность обучения заметно снижается. При двоичных входных векторах в среднем половина весовых коэффициентов не будет корректироваться, поэтому область возможных значений выходов нейронов (0, 1) желательно сдвинуть в пределы (-0,5, 0,5), что достигается простыми модификациями логистических функций. Например, сигмоид с экспонентой преобразуется к виду:
Рассмотрим вопрос о емкости нейронной сети, т. е. числа образов, предъявляемых на ее входы, которые она способна научиться распознавать. Для сетей с числом слоев больше двух, этот вопрос остается открытым. Для сетей с двумя слоями, детерминистская емкость сети Са оценивается следующим образом:
где Lw - число подстраиваемых весов, т - число нейронов в выходном слое.
Данное выражение получено с учетом некоторых ограничений. Во-первых, число входов n и нейронов в скрытом слое L должно удовлетворять неравенству (n+L) > т. Во-вторых, LwJm > 1000. Однако приведенная оценка выполнена для сетей с пороговыми активационными функциями нейронов, а емкость сетей с гладкими активационными функциями, например (1.23), обычно больше. Кроме того, термин детерминистский означает, что полученная оценка емкости подходит для всех входных образов, которые могут быть представлены n входами. В действительности распределение входных образов, как правило, обладает некоторой регулярностью, что позволяет нейронной сети проводить обобщение и, таким образом, увеличивать реальную емкость. Так как распределение образов, в общем случае, заранее не известно, можно говорить о реальной емкости только предположительно, но обычно она раза в два превышает детерминистскую емкость.
Вопрос о емкости нейронной сети тесно связан с вопросом о требуемой мощности выходного слоя сети, выполняющего окончательную классификацию образов. Например, для разделения множества входных образов по двум классам достаточно одного выходного нейрона. При этом каждый логический уровень («1» и «О») будет обозначать отдельный класс. На двух выходных нейронах с пороговой функцией активации можно закодировать уже четыре класса. Для повышения достоверности классификации желательно ввести избыточность путем выделения каждому классу одного нейрона в выходном слое или, что еще лучше, нескольких, каждый из которых обучается определять принадлежность образа к классу со своей степенью достоверности, например: высокой, средней и низкой. Такие нейронные сети позволяют проводить классификацию входных образов, объединенных в нечеткие (размытые или пересекающиеся) множества. Это свойство приближает подобные сети к реальным условиям функционирования биологических нейронных сетей.
Рассматриваемая нейронная сеть имеет несколько «узких мест». Во-первых, в процессе большие положительные или отрицательные значения весов могут сместить рабочую точку на сигмоидах нейронов в область насыщения. Малые величины производной от логистической функции приведут в соответствии с (1.15) и (1.16) к остановке обучения, что парализует сеть. Во-вторых, применение метода градиентного спуска не гарантирует нахождения глобального минимума целевой функции. Это тесно связано вопросом выбора скорости обучения. Приращения весов и, следовательно, скорость обучения для нахождения экстремума должны быть бесконечно малыми, однако в этом случае обучение будет
происходить неприемлемо медленно. С другой стороны, слишком большие коррекции весов могут привести к постоянной неустойчивости процесса обучения. Поэтому в качестве коэффициента скорости обучения η обычно выбирается число меньше 1 (например, 0,1), которое постепенно уменьшается в процессе обучения. Кроме того, для исключения случайных попаданий сети в локальные минимумы иногда, после стабилизации значений весовых коэффициентов, η кратковременно значительно увеличивают, чтобы начать градиентный спуск из новой точки. Если повторение этой процедуры несколько раз приведет сеть в одно и то же состояние, можно предположить, что найден глобальный минимум.
Существует другой метод исключения локальных минимумов и паралича сети, заключающийся в применении стохастических нейронных сетей.
Дадим изложенному геометрическую интерпретацию.
В алгоритме обратного распространения вычисляется вектор градиента поверхности ошибок. Этот вектор указывает направление кратчайшего спуска по поверхности из текущей точки, движение по которому приводит к уменьшению ошибки. Последовательность уменьшающихся шагов приведет к минимуму того или иного типа. Трудность здесь представляет вопрос подбора длины шагов.
При большой величине шага сходимость будет более быстрой, но имеется опасность перепрыгнуть через решение или в случае сложной формы поверхности ошибок уйти в неправильном направлении, например, продвигаясь по узкому оврагу с крутыми склонами, прыгая с одной его стороны на другую. Напротив, при небольшом шаге и верном направлении потребуется очень много итераций. На практике величина шага берется пропорциональной крутизне склона, так что алгоритм замедляет ход вблизи минимума. Правильный выбор скорости обучения зависит от конкретной задачи и обычно делается опытным путем. Эта константа может также зависеть от времени, уменьшаясь по мере продвижения алгоритма.
Обычно этот алгоритм видоизменяется таким образом, чтобы включать слагаемое импульса (или инерции). Это способствует продвижению в фиксированном направлении, поэтому, если было сделано несколько шагов в одном и том же направлении, то алгоритм увеличивает скорость, что иногда позволяет избежать локального минимума, а также быстрее проходить плоские участки.
На каждом шаге алгоритма на вход сети поочередно подаются все обучающие примеры, реальные выходные значения сети сравниваются с требуемыми значениями, и вычисляется ошибка. Значение ошибки, а также градиента поверхности ошибок используется для корректировки весов, после чего все действия повторяются. Процесс обучения прекращается либо когда пройдено определенное количество эпох, либо когда ошибка достигнет некоторого определенного малого уровня, либо когда ошибка перестанет уменьшаться.
Рассмотрим проблемы обобщения и переобучения нейронной сети более подробно. Обобщение - это способность нейронной сети делать точный прогноз на данных, не принадлежащих исходному обучающему множеству. Переобучение же представляет собой чрезмерно точную подгонку, которая имеет место, если алгоритм обучения работает слишком долго, а сеть слишком сложна для такой задачи или для имеющегося объема данных.
Продемонстрируем проблемы обобщения и переобучения на примере аппроксимации некоторой зависимости не нейронной сетью, а посредством полиномов, при этом суть явления будет абсолютно та же.
Графики полиномов могут иметь различную форму, причем, чем выше степень и число членов, тем более сложной может быть эта форма. Для исходных данных можно подобрать полиномиальную кривую (модель) и получить, таким образом, объяснение имеющейся зависимости. Данные могут быть зашумлены, поэтому нельзя считать, что лучшая модель в точности проходит через все имеющиеся точки. Полином низкого порядка может лучше объяснять имеющуюся зависимость, однако, быть недостаточно гибким средством для аппроксимации данных, в то время как полином высокого порядка может оказаться чересчур гибким, но будет точно следовать данным, принимая при этом замысловатую форму, не имеющую никакого отношения к настоящей зависимости.
Нейронные сети сталкивается с такими же трудностями. Сети с большим числом весов моделируют более сложные функции и, следовательно, склонны к переобучению. Сети же с небольшим числом весов могут оказаться недостаточно гибкими, чтобы смоделировать имеющиеся зависимости. Например, сеть без скрытых слоев моделирует лишь обычную линейную функцию.
Как же выбрать правильную степень сложности сети? Почти всегда более сложная сеть дает меньшую ошибку, но это может свидетельствовать не о хорошем качестве модели, а о переобучении сети.
Выход состоит в использовании контрольной кросс-проверки. Для этого резервируется часть обучающей выборки, которая используется не для обучения сети по алгоритму обратного распространения ошибки, а для независимого контроля результата в ходе алгоритма. В начале работы ошибка сети на обучающем и контрольном множествах будет одинаковой. По мере обучения сети ошибка обучения убывает, как и ошибка на контрольном множестве. Если же контрольная ошибка перестала убывать или даже стала расти, это указывает на то, что сеть начала слишком близко аппроксимировать данные (переобучилась) и обучение следует остановить. Если это случилось, то следует уменьшить число скрытых элементов и/или слоев, ибо сеть является слишком мощной для данной задачи. Если же обе ошибки (обучения и кросс-проверки) не достигнут достаточного малого уровня, то переобучения, естественно не произошло, а сеть, напротив, является недостаточно мощной для моделирования имеющейся зависимости.
Описанные проблемы приводят к тому, что при практической работе с нейронными сетями приходится экспериментировать с большим числом различных сетей, порой обучая каждую из них по несколько раз и сравнивая полученные результаты. Главным показателем качества результата является здесь контрольная ошибка. При этом, в соответствии с общесистемным принципом, из двух сетей с приблизительно равными ошибками контроля имеет смысл выбрать ту, которая проще.
Необходимость многократных экспериментов приводит к тому, что контрольное множество начинает играть ключевую роль в выборе модели и становится частью процесса обучения. Тем самым ослабляется его роль как независимого критерия качества модели. При большом числе экспериментов есть большая вероятность выбрать удачную сеть, дающую хороший результат на контрольном множестве. Однако для того чтобы придать окончательной модели должную надежность, часто (когда объем обучающих примеров это позволяет) поступают следующим образом: резервируют тестовое множество примеров. Итоговая модель тестируется на данных из этого множества, чтобы убедиться, что результаты, достигнутые на обучающем и контрольном множествах примеров, реальны, а не являются артефактами процесса обучения. Разумеется, для того чтобы хорошо играть свою роль, тестовое множество должно быть использовано только один раз: если его использовать повторно для корректировки процесса обучения, то оно фактически превратится в контрольное множество.
С целью ускорения процесса обучения сети предложены многочисленные модификации алгоритма обратного распространения ошибки, связанные с использованием различных функций ошибки, процедур определения направления и величин шага.
1) Функции ошибки:
• интегральные функции ошибки по всей совокупности обучающих примеров;
• функции ошибки целых и дробных степеней.
2) Процедуры определения величины шага на каждой итерации:
• дихотомия;
• инерционные соотношения (см. выше);
• отжиг.
3) Процедуры определения направления шага:
• с использованием матрицы производных второго порядка
(метод Ньютона);
• с использованием направлений на нескольких шагах
(партан метод).
1.4.2. Обучение без учителя
Рассмотренный алгоритм обратного распространения ошибки подразумевает наличие некоего внешнего звена, предоставляющего нейронной сети, кроме входных, целевые выходные образы. Алгоритмы, основанные на подобной концепции, называются алгоритмами обучения с учителем. Для их успешного функционирования необходимо наличие экспертов, задающих на предварительном этапе для каждого входного образа эталонный выходной. Так как создание интеллектуальных систем базируется, во многом, на биологических прототипах, до сих пор не прекращается спор о том, можно ли считать алгоритмы обучения с учителем натуральными или же они полностью искусственны. Например, обучение человеческого мозга, на первый взгляд, происходит без учителя: на зрительные, слуховые, тактильные и прочие рецепторы поступает информация извне, и внутри нервной системы происходит некая самоорганизация. Однако, нельзя отрицать и того, что в жизни человека немало учителей (и в буквальном, и в переносном смысле), которые координируют внешние воздействия. Вместе в тем, чем бы ни закончился спор приверженцев этих концепций обучения, они обе имеют право на существование.
Главная черта, делающая обучение без учителя привлекательным, это его самостоятельность. Процесс обучения, как и в случае обучения с учителем, заключается в подстраивании весов синапсов. Некоторые алгоритмы, правда, изменяют и структуру сети, т. е. количество нейронов и их взаимосвязи, но такие преобразования правильнее назвать более широким термином - самоорганизацией. Очевидно, что подстройка весов синапсов может проводиться только на основании информации о состоянии нейронов и уже имеющихся весовых коэффициентов). На этом, в частности, по аналогии с известными принципами самоорганизации нервных клеток, построены алгоритмы обучения Хебба.
Сигнальный метод обучения Хебба заключается в изменении весов по следующему правилу:
wij(t) = wij(t-1) + α уi(q-1)уj(q) (1.25)
где уi(q-1) - выходное значение нейрона i слоя (q-1), уj(q) - выходное значение нейрона j слоя q; wij(t)и wij(t-1) - весовой коэффициент синапса, соединяющего эти нейроны, на итерациях t и (t-1) соответственно; α - коэффициент скорости обучения. Здесь и далее, для общности, под q подразумевается произвольный слой сети.
При обучении по данному методу усиливаются связи между возбужденными нейронами.
Существует также и дифференциальный метод обучения Хебба, определяемый соотношением:
wij(t) = wij(t-1)+α( уi(q-1)(t)-yi(q-1)(t-1))·( уj(q)(t)-yj(q)(t-
Здесь уi(q-1)(t) и yi(q-1)(t-1) - выходное значение нейрона i слоя (q -1) соответственно на итерациях t и (t-1); уj(q)(t) и yj(q)(t-1) - то же самое для нейрона j слоя q. Как видно из формулы (1.26), более интенсивно обучаются синапсы, соединяющие нейроны, выходы которых наиболее динамично изменились в сторону увеличения.
Полный алгоритм обучения с применением вышеприведенных формул будет выглядеть следующим образом.
ШАГ 1. На стадии инициализации всем весовым коэффициентам присваиваются небольшие случайные значения.
ШАГ 2. На входы сети подается входной образ, и сигналы возбуждения распространяются по всем слоям согласно принципам классических сетей прямого распространения (feedforward). При этом для каждого нейрона рассчитывается взвешенная сумма его входов, к которой затем применяется активационная функция нейрона, в результате чего получается его выходное значение уi(q), i = 1... Lq, где Lq - число нейронов в слое q, q = 1...Q; Q - число слоев в сети.
ШАГ 3. На основании полученных выходных значений нейронов по формуле (1.25) или (1.26) проводится изменение весовых коэффициентов.
ШАГ 4. Цикл с шага 2, пока выходные значения сети не стабилизируются с заданной точностью. Применение этого способа определения момента завершения обучения, отличного от использовавшегося для сети обратного распространения, обусловлено тем, что подстраиваемые значения синапсов фактически не ограничены. На шаге 2 цикла попеременно предъявляются все образы из входного набора.
Следует отметить, что вид откликов на каждый класс входных образов заранее неизвестен и представляет собой произвольное сочетание состояний нейронов выходного слоя, обусловленное случайным распределением весов на стадии инициализации. Вместе с тем, сеть способна обобщать схожие образы, относя их к одному классу. Тестирование обученной сети позволяет определить топологию классов в выходном слое. Для приведения откликов обученной сети к удобному представлению можно дополнить сеть одним слоем, который, например, по алгоритму обучения однослойного персептрона необходимо заставить отображать выходные реакции сети в требуемые образы.
Другой алгоритм обучения без учителя - алгоритм Кохоне на - предусматривает подстройку синапсов на основании их значений на предыдущей итерации:
wij(t) = wij(t-1) + α( уi(q-1)-wi (t-1
Из выражения (1.27) видно, что обучение сводится к минимизации разницы между входными сигналами нейрона, поступающими с выходов нейронов предыдущего слоя уi(q-1), и весовыми коэффициентами его синапсов.
Полный алгоритм обучения имеет примерно такую же структуру, как в методах Хебба, но на шаге 3 из всего слоя выбирается нейрон, значения синапсов которого максимально походят на входной образ, и подстройка весов по формуле (1.27) проводится только для него. Эта, так называемая, аккредитация может сопровождаться торможением всех остальных нейронов слоя и введением выбранного нейрона в насыщение. Выбор такого нейрона может осуществляться, например, расчетом скалярного произведения вектора весовых коэффициентов с вектором входных значений. Максимальное произведение дает выигравший нейрон.
Другой вариант состоит в расчете расстояния между этими векторами в R-мерном пространстве:
где R - размерность векторов; j - индекс нейрона в слое q; i - индекс суммирования по нейронам слоя (q -1); wij - вес синапса, соединяющего нейроны; выходы нейронов слоя (q-1) являются входными значениями для слоя q.
В данном случае, побеждает нейрон с наименьшим расстоянием. Иногда слишком часто получающие аккредитацию нейроны принудительно исключаются из рассмотрения, чтобы уравнять права всех нейронов слоя. Простейший вариант такого алгоритма заключается в торможении только что выигравшего нейрона.
С целью сокращения длительности процесса обучения при использовании алгоритма Кохонена существует практика нормализации входных образов и начальных значений весовых коэффициентов на стадии инициализации в соответствии с выражениями:
 |
где xi - i-й компонент вектора входного образа или вектора весовых коэффициентов, a n - его размерность.
Инициализация весовых коэффициентов случайными значениями может привести к тому, что различные классы, которым соответствуют плотно распределенные входные образы, сольются или, наоборот, раздробятся на дополнительные подклассы в случае близких образов одного и того же класса. Для избежания такой ситуации используется метод выпуклой комбинации. Суть его сводится к тому, что входные нормализованные образы подвергаются преобразованию:
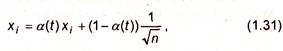 |
где α(t) - коэффициент, изменяющийся в процессе обучения от нуля до единицы, в результате чего вначале на входы сети подаются практически одинаковые образы, а с течением времени они все больше сходятся к исходным.
После выбора из слоя q нейрона j с минимальным расстоянием di по формуле (1.28) производится обучение по формуле (1.27) не только этого нейрона, но и его соседей, расположенных в окрестности Ω. Величина Ω для первых итераций очень большая, так что обучаются все нейроны, но с течением времени она уменьшается до нуля. Таким образом, чем ближе окончание обучения, тем точнее определяется группа нейронов, отвечающих каждому классу образов.
На основе рассмотренного выше метода строятся самоорганизующиеся нейронные сети (self-organizing feature maps). Этот устоявшийся перевод с английского представляется не вполне удачным, так как речь идет не об изменении структуры сети, а только о подстройке синапсов нейронов.
1.5. Настройка числа нейронов в скрытых слоях
многослойных нейронных сетей
в процессе обучения
Для того, чтобы многослойная нейронная сеть реализовывала заданное обучающей выборкой отображение, она должна иметь достаточное число нейронов в скрытых слоях. В настоящее время нет формул для точного определения необходимого числа нейронов в сети по заданной обучающей выборке. Однако предложены способы настройки числа нейронов в процессе обучения, которые обеспечивают построение нейронной сети для решения задачи и дают возможность избежать избыточности. Эти способы настройки можно разделить на две группы: алгоритмы сокращения (pruning algorithms) и конструктивные алгоритмы (constructive algorithms).
1.5.1. Алгоритмы сокращения
В начале работы алгоритма обучения с сокращением число нейронов в скрытых слоях сети заведомо избыточно. Затем из нейронной сети постепенно удаляются синапсы и нейроны. Существуют два подхода к реализации алгоритмов сокращения.
1) Метод штрафных функций.
В целевую функцию алгоритма обучения вводится штрафы за то, что значения синаптических весов отличны от нуля, например:
где wij - синаптический вес, i - номер нейрона, j - номер входа; L -число нейронов скрытого слоя, n - размерность входного сигнала.
2) Метод проекций.
Синаптический вес обнуляется, если его значение попало в заданный диапазон:
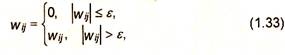 |
где ε - некоторая константа.
Алгоритмы сокращения имеют, по крайней мере, два недостатка:
• нет методики определения числа нейронов скрытых слоев, которое является избыточным, поэтому перед началом работы алгоритма нужно угадать это число;
• в процессе работы алгоритма сеть содержит избыточное
число нейронов, поэтому обучение идет медленно.
1.5.2. Конструктивные алгоритмы
Предшественником конструктивных алгоритмов можно считать методику обучения многослойных нейронных сетей, включающую в себя следующие шаги:
ШАГ 1. Выбор начального числа нейронов в скрытых слоях.
ШАГ 2. Инициализация сети, заключающаяся в присваивании синаптическим весам и смещениям сети случайных значений из заданного диапазона.
ШАГ 3. Обучение сети по заданной выборке.
ШАГ 4. Завершение в случае успешного обучения. Если сеть обучить не удалось, то число нейронов увеличивается и повторяются шаги со второго по четвертый.
В конструктивных алгоритмах число нейронов в скрытых слоях также изначально мало и постепенно увеличивается. В отличие от этой методики, в конструктивных алгоритмах сохраняются навыки, приобретенные сетью до увеличения числа нейронов.
Конструктивные алгоритмы различаются правилами задания значений параметров в новых, добавленных в сеть, нейронах:
• значения параметров являются случайными числами из
заданного диапазона;
• значения синаптических весов нового нейрона определяются путем расщепления (splitting) одного из старых нейронов.
Первое правило не требует значительных вычислений, однако его использование приводит к некоторому увеличению значения функции ошибки после каждого добавления нового нейрона. В результате случайного задания значений параметров новых нейронов может появиться избыточность в числе нейронов скрытого слоя. Расщепление нейронов лишено двух указанных недостатков. Суть алгоритма расщепления проиллюстрирована на рис. 1.7.
На этом рисунке показан вектор весов нейрона скрытого слоя на некотором шаге обучения и векторы изменения весов, соответствующие отдельным обучающим примерам. Векторы изменений имеют два преимущественных направления и образуют в пространстве область, существенно отличающуюся от сферической. Суть алгоритма заключается в выявлении и расщеплении таких нейронов. В результате расщепления вместо одного исходного в сети оказывается два нейрона. Первый из этих нейронов имеет вектор весов, представляющий из себя сумму вектора весов исходного нейрона и векторов изменений весов одного из преимущественных направлений. В результате суммирования векторов изменений весов другого преимущественного направления и вектора весов исходного нейрона получают синаптические веса второго нового нейрона.
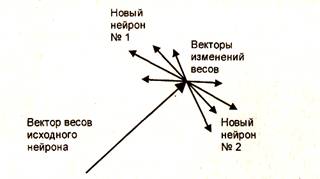 |
Рис. 1.7. Вектор весов нейрона скрытого слоя и изменения, соответствующие отдельным обучающим примерам
Расщеплять нейроны, векторы изменений которых имеют два преимущественных направления, необходимо потому, что наличие таких нейронов приводит к осцилляциям при обучении методом обратного распространения. При обучении методом с интегральной функцией ошибки наличие таких нейронов приводит к попаданию в локальный минимум с большим значением ошибки.
Алгоритм расщепления включает в себя:
• построение ковариационной матрицы векторов изменений синаптических весов;
• вычисление собственных векторов и собственных значений полученной матрицы с помощью итерационного алгоритма Ойа (Oja), в соответствии с которым выполняется стохастический градиентный подъем и ортогонализация Грамма-Шмидта.
Недостатком алгоритма является экспоненциальный рост времени вычислений при увеличении размерности сети.
Для преодоления указанного недостатка предложен упрощенный алгоритм расщепления, который не требует значительных вычислений. Общее число нейронов в сети, построенной с помощью этого алгоритма по заданной обучающей выборке, может быть несколько больше, чем у сети, построенной с помощью исходного алгоритма.
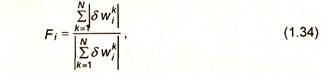 |
В упрощенном алгоритме для расщепления выбирается нейрон с наибольшим значением функционала:
где δw - вектор изменений синаптических весов нейрона; i - номер нейрона; i = 1... L, L - число нейронов; k - номер обучающего примера; N - число примеров в обучающей выборке.
Таким образом, в качестве критерия выбора нейрона для расщепления используется отношение суммы длин векторов изменений синаптических весов нейрона, соответствующих различным обучающим примерам, к длине суммы этих векторов.
В результате расщепления вместо исходного нейрона в сеть вводятся два новых нейрона. Значение каждого синаптического веса нового нейрона есть значение соответствующего веса старого нейрона плюс некоторый небольшой шум. Величины весов связей выходов новых нейронов и нейронов следующего слоя равны половине величин весов связей исходного нейрона с соответствующими весами следующего слоя. Упрощенный алгоритм, как и исходный, гарантирует, что функция ошибки после расщепления увеличиваться не будет.
Кроме описанных способов выбора нейронов для расщепления, может быть использован анализ чувствительности, в процессе которого строятся матрицы Гессе для вторых производных функции ошибки по параметрам сети. По величине модуля второй производной судят о важности значения данного параметра для решения задачи. Параметры с малыми значениями вторых производных обнуляют. Анализ чувствительности требует больших вычислительных ресурсов.
Дополнительная информация об алгоритмах обучения приведена в приложении.
1.6. Краткое обобщение материалов главы
1.6.1. Как построить нейронную сеть
Практически любую задачу можно свести к задаче, решаемой нейронной сетью. В табл. 1.2 показано, каким образом следует сформулировать в терминах нейронной сети задачу распознавания рукописных букв.
Таблица 1.2
Задача распознавания рукописных букв в терминах нейронной сети
Задача распознавания рукописных букв | |
Дано: растровое черно-белое изображение буквы размером 30x30 пикселов | Необходимо: распознать предъявленную букву (в алфавите 33 буквы) |
Формулировка задачи для нейронной сети | |
Дано: входной вектор из 900 двоичных символов (900 = 30x30) | Необходимо: построить нейронную сеть с 900 входами и 33 выходами, которые помечены буквами. Номер нейрона с максимальным значением выходного сигнала должен соответствовать предъявленному изображению буквы. |
Интерес представляет не аналоговое значение выхода, а номер класса (номер буквы в алфавите). Поэтому каждому классу сопоставляется свой выходной нейрон, а ответом сети считается номер класса, соответствующий нейрону, на чьем выходе уровень сигнала максимален. Значение же уровня сигнала на выходе характеризует достоверность того, что на вход была подана соответствующая рукописная буква.
Нейронная сеть строится в два этапа.
1) Выбор типа (архитектуры) сети.
2) Подбор весов (обучение) сети.
На первом этапе необходимо определить следующее:
• какие нейроны использовать (число входов, функции активации);
• каким образом следует соединить нейроны между собой;
• что взять в качестве входов и выходов сети.
Нет необходимости придумывать нейронную сеть «с нуля», так как существуют несколько десятков различных нейросетевых архитектур, причем эффективность многих из них доказана математически. Наиболее популярные и изученные из них - это многослойный персептрон, нейронная сеть с общей регрессией, сети Кохонена и другие, которые будут рассмотрены ниже.
На втором этапе производится обучение выбранной сети посредством настройки ее весов. Количество весов может быть велико, поэтому обучение представляет собой сложный и длительный процесс. Для многих архитектур разработаны специальные алгоритмы обучения, наиболее популярный из которых алгоритм обратного распространения ошибки.
1.6.2. Обучение нейронной сети
Обучить нейронную сеть это значит, сообщить ей, чего от нее добиваются. Этот процесс похож на обучение ребенка алфавиту. Показав ребенку изображение буквы и получив неверный ответ, ему сообщается тот ответ, который хотят получить. Ребенок запоминает этот пример вместе с верным ответом и в его памяти происходят некоторые изменения в нужном направлении.
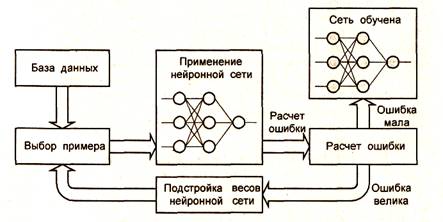
Процесс обучения заключается в последовательном предъявлении букв (рис. 1.8).
При предъявлении изображения каждой буквы на входе сеть выдает некоторый ответ, не обязательно верный. Известен и верный (желаемый) ответ. В данном случае желательно, чтобы на выходе соответствующего нейрона уровень сигнала был максимален. Обычно в качестве желаемого в задаче классификации берут набор, где «1» стоит на выходе этого нейрона, а «О» - на выходах всех остальных нейронов. Одну и ту же букву (а также различные изображения одной и той же буквы) можно предъявлять сети много раз.
После многократного предъявления примеров веса сети стабилизируются, причем сеть дает правильные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что сеть обучена. В программных реализациях можно видеть, что в процессе обучения величина ошибки (сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда величина ошибки достигает нуля или приемлемо малого уровня, обучение останавливают, и сеть готова к распознаванию.
 |
Важно отметить, что вся информация, которую сеть приобретает о задаче, содержится в наборе примеров. Поэтому качество обучения сети зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают задачу. Считается, что для полноценной тренировки требуется хотя бы несколько десятков (а лучше сотен) примеров.
Рис. 1.8. Процесс обучения нейронной сети
1.6.3. Применение обученной нейронной сети
Важнейшая особенность человеческого мозга состоит в том, что, однажды обучившись определенному процессу, он может верно действовать и в тех ситуациях, которым он не обучался. Так же и обученная нейронная сеть может с большой вероятностью правильно реагировать на новые, не предъявленные ей ранее данные. Например, можно нарисовать букву другим почерком, а затем предложить нейронной сети классифицировать новое изображение. Веса обученной сети хранят достаточно много информации о сходстве и различиях букв, поэтому можно рассчитывать на правильный ответ и для нового варианта изображения.
Отметим, что задачи классификации (типа распознавания букв) очень плохо алгоритмизируются. Если в случае распознавания букв верный ответ очевиден заранее, то в более сложных практических задачах обученная нейронная сеть выступает как эксперт, обладающий большим опытом и способный дать ответ на трудный вопрос. Примером такой задачи служит медицинская диагностика, где сеть может учитывать большое количество числовых параметров (энцефалограмма, давление, вес). Конечно, «мнение» сети в этом случае нельзя считать окончательным.
Классификация предприятий по степени их перспективности - это уже привычный способ использования нейронных сетей в практике западных компаний. При этом сеть также использует множество экономических показателей, сложным образом связанных между собой.
Нейросетевой подход особенно эффективен в задачах экспертной оценки по той причине, что он сочетает в себе способность компьютера к обработке чисел и способность мозга к обобщению и распознаванию. Говорят, что у хорошего врача способность к распознаванию в своей области столь велика, что он может провести приблизительную диагностику уже по внешнему виду пациента. Можно согласиться также, что опытный трейдер чувствует направление движения рынка по виду графика. Однако в первом случае все факторы наглядны, т. е. характеристики пациента мгновенно воспринимаются мозгом как «бледное лицо», «блеск в глазах». Во втором же случае учитывается только один фактор - курс за определенный период времени. Нейронная сеть позволяет обрабатывать огромное количество факторов (до нескольких тысяч), независимо от их наглядности. Это универсальный «хороший врач», который может поставить свой диагноз в любой области.
Помимо задач классификации, нейронные сети широко используются для поиска зависимостей в данных и кластеризации. Кластеризация - это разбиение набора примеров на несколько компактных областей (кластеров), причем число кластеров заранее неизвестно. Кластеризация позволяет представить неоднородные данные в более наглядном виде и использовать далее для исследования каждого кластера различные методы. Например, нейронная сеть на основе методики использования МГУА (метода группового учета аргументов) позволяет по обучающей выборке построить зависимость одного параметра от других в виде полинома. Такая сеть может не только мгновенно выучить таблицу умножения, но и найти сложные скрытые зависимости в данных (например, финансовых), которые не обнаруживаются стандартными статистическими методами, быстро выявить фальсифицированные страховые случаи или недобросовестные предприятия.
Особенно важны для практики, в частности, для финансовых приложений, задачи прогнозирования, поэтому поясним способы применения нейронных сетей в этой области более подробно.
Рассмотрим задачу прогнозирования курса акций на день вперед. Пусть имеется база данных, содержащая значения курса за последние 300 дней. Построим прогноз завтрашней цены на основе курсов за последние несколько дней. Понятно, что прогнозирующая нейронная сеть должна иметь всего один выход и столько входов, сколько предыдущих значений мы хотим использовать для прогноза, например, четыре последних значения. Составить обучающий пример очень просто, входными значениями будут курсы за четыре последних дня, а желаемым выходом - известный курс в следующий за ними день.
Если нейронная сеть совместима с какой-либо системой обработки электронных таблиц (например, Excel), то подготовка обучающей выборки состоит из следующих операций:
• занести значения курса акций последовательно в столбец таблицы;
• скопировать значения котировок в 4 соседних столбца;
• сдвинуть второй столбец на 1 ячейку вверх, третий столбец - на 2 и т. д. (рис.1.9).
Смысл этой подготовки состоит в том, что каждая строка таблицы теперь представляет собой обучающий пример, где первые четыре числа - входные значения сети, а пятое число - желаемое значение выхода. Исключение составляют последние четыре строки, где данных недостаточно. Поэтому эти строки не учитываются при обучении. Заметим, что в четвертой снизу строке заданы все четыре входных значения, но неизвестно значение выхода. Именно при применении к этой строке обученной сети и можно получить прогноз на следующий день.
Как видно из этого примера, объем обучающей выборки зависит от выбранного количества входов. Если сделать 299 входов, то такая сеть потенциально могла бы строить лучший прогноз, чем сеть с 4 входами, однако в этом случае имеется всего один обучающий пример, и обучение бессмысленно. Это следует учитывать при выборе числа входов, выбирая разумный компромисс между глубиной предсказания (число входов) и качеством обучения (объем обучающей выборки).
Укажем в заключение, что ряд практических примеров использования нейронных сетей приведен в третьей части книги.
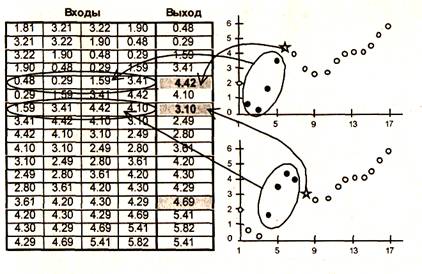 |
Рис. 1.9. Подготовка данных для нейронной сети в Excel





