Московский инженерно-физический институт (государственный университет)
1Центр гравитации и фундаментальной метрологии ВНИИМС, Москва
ИНФЛЯЦИЯ И ДОПОЛНИТЕЛЬНЫЕ ИЗМЕРЕНИЯ
В работе получен потенциал инфлатонного поля в рамках нелинейной гравитации с дополнительными измерениями. Подбором параметров удается получить вид потенциала, удовлетворяющий основным требованиям к инфляции, стадии нагрева Вселенной и наблюдаемое значение космологической постоянной в современную эпоху.
Инфляционный сценарий позволяет решить трудности, возникающие в фридмановской модели горячей Вселенной. А именно:
1) проблема сингулярности;
2) проблема горизонта и плоскостности;
3) формирование крупномасштабной структуры;
4) анизотропия микроволнового фона;
5) проблема магнитных монополей и многие другие.
Рассмотрим простейший случай квадратичной зависимости потенциальной энергии инфлатонного поля от величины поля φ. За счет квантовых эффектов в некий момент времени образуется однородная флуктуация поля с характерным размером 
. Затем происходит скатывание поля к минимуму энергии. Запишем лагранжиан инфлатонного поля в виде:
где V(φ) – потенциальная энергия инфлатонного поля. Тогда уравнение, описывающее поведение поля φ во время инфляции с точки зрения внутреннего наблюдателя, имеет следующий вид:
,
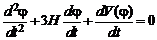(здесь 
– параметр Хаббла). Масштабный фактор, удовлетворяющий данному уравнению, зависит от времени следующим образом
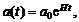
с уравнением состояния на инфляционной стадии вида
.
Современные измерения [1, 2] дают значение:
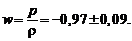
Ниже представлены данные WMAP [1] о плотностях темной энергии (индекс V), темной материи (индекс D), барионов (индекс B) и излучения (индекс R) в единицах критической плотности:
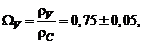
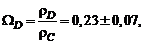
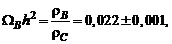
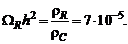
(Здесь h – параметр Хаббла, измеренный в единицах 100 км ∙ с–1 ∙ Мпк–1.)
Рассмотрим теперь ситуацию, возникающую при введении дополнительных измерений. Действие в D-мерном пространстве-времени имеет вид:
(
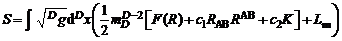
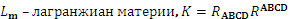). После редукции к четырем измерениям удается получить следующую зависимость потенциальной энергии инфлатонного поля от величин полей φ1 и φ2 (рассматриваются два фактор-пространства с размерностями d1 и d2 соответственно):
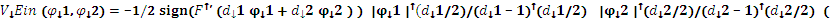
(здесь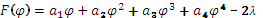 
).
При нижеприведенных значениях входящих в формулы параметров был построен график зависимости потенциальной энергии инфлатонного поля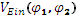 
(рис. 1):
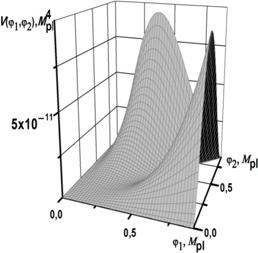
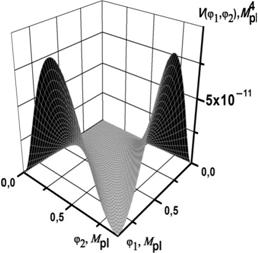
Рис. 1. График зависимости потенциальной энергии инфлатонного поля от величин полей φ1 и φ2
Из рисунка видно, что потенциал полей имеет участок, в котором происходят колебания этих полей около минимума (инфляция). После окончания инфляции поля движутся вдоль долины (приближенно)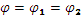 
, приближаясь к нулю. Это означает монотонный рост размеров дополнительного пространства с одновременным уменьшением космологической постоянной. Очевидно, что в некий момент наступает стадия вторичного медленного скатывания, когда динамика сильно упрощается и может быть описана аналитически. Описание полей сразу по окончании инфляции возможно лишь при численном решении уравнения:
(
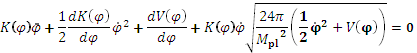
– кинетический член, 
– масса Планка).
После того как система вышла на вторую стадию медленного скатывания, классическое уравнение может быть упрощено. Пренебрежем слагаемыми, содержащими 
, а также оставим главные члены в разложении по 
потенциала и кинетического члена, получим уравнение вида
.
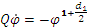Здесь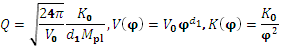 
. Решение этого уравнения
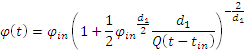
медленно убывает.
Результаты численных расчетов позволяют найти “начальные” значения: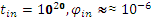 
. Теперь мы можем определить величину поля и значение потенциала 
в современную эпоху, т. е. при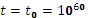 
в планковских единицах:
.
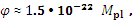
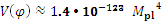По полученной величине поля в современную эпоху может быть оценен размер дополнительных пространств:
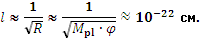
Таким образом, используя вид потенциала инфлатонного поля, полученный в рамках чистой нелинейной гравитации с дополнительными измерениями, удалось добиться следующего:
1) получить инфляционную стадию вместе со стадией постинфляционного нагрева;
2) получить наблюдаемую плотность темной энергии (
).
СПИСОК ЛИТЕРАТУРЫ
1. Spergel D.N. et al. // astro-ph/0603449. Astrophys. J. Suppl. 2007. V. 170. P. 377.
2. Riess A. G. et al. // astro-ph/0611572. Astrophys. J. 20
3. Bronnikov K. A.,Rubin S. G. // Gravitation and Cosmology. 2007. Vol. 13. №P. 191.
4. Cornell University Library [Электронный ресурс] : 27 Feb 2007 (arXiv:gr-qc/0610003v2) : Режим доступа к журналу: http//www. arXiv. org.
5. // УФН. 2008. Т. 178. № 3.
