для проведения промежуточного контроля знаний
№ п/п | Вопрос | Варианты ответов |
Введение в исследование операций. Основы классической теории оптимизации | ||
1. | Что означает термин «исследование операций»? | · Поиск наилучших планов · Планирование производства · Применение математических методов для обоснования решений · решение систем уравнений · нет правильного ответа |
2. | Каковы на Ваш взгляд основные цели применения аппарата Системного анализа? | · моделирование явлений и процессов реального мира с точностью, достаточной для их адекватного восприятия · изучение явлений и процессов реального мира · изучение способов функционирования явлений и процессов реального мира · построение алгоритмов · нет правильного ответа |
3. | Какие задачи относитсятся к теория исследования операций | · линейное программирование · имитационное моделирование · статистический анализ данных

|
4. | Чем отличаются задачи безусловной и условной оптимизации | · числом переменных; · наличием ограничений; · учетом фактора времени |
5. | Объясните разницу между задачами линейного и нелинейного программирования | · линейные ограничения · линейная целевая функция · Линейные и то и другое · хотя бы что то нелинейно |
6. | Задача математического программирования не имеет допустимых решений. Выберите ситуацию, возможную при данном условии | · В задаче отсутствуют ограничения · Система ограничений задачи несовместна · Целевая функция неограниченна на допустимой области |
7. | Расставьте в порядке значимости условия решения задачи одномерной оптимизации | · целевая функция · ограничения на решение целевой функции · наличие ограничений на диапазон независимых факторов · наличие мощной вычислительной техники |
8. | Стационарная точка выпуклой функции является | · седловой точкой · точкой локального максимума · точкой локального минимума |
9. | Стационарная точка вогнутой функции является | · седловой точкой · точкой максимума · точкой минимума |
10. | Графический анализ функции позволяет | · определить характер функции · выявить точки локального экстремума · определить точки глобального экстремума |
11. | Задача проектирования контейнера заданного объема относится к задачам: | · безусловной оптимизации · условной оптимизации · динамического программирования |
12. | Вектор градиента функции f(x) в точке x(k) направлен в сторону | · минимума функции · наискорейшего возрастания функции · наискорейшего убывания функции · максимума функции · седловой точки |
13. | Как вектор градиента функции f(x) в точке x(k) направлен относительно линии уровня | · параллельно · перпендикулярно · перпендикулярно в обратную сторону |
14. | Вектор градиента функции f(x) в точке экстремума равен | · максимальному значению · нулю · минимальному значению |
15. | Задача | · безусловной оптимизации; · нелинейного программирования · линейного программирования |
16. | Экстремум функции это: | · минимум функции · максимум · минимум или максимум |
17. | Впишите в утверждение нужный термин | Минимальное или максимальное значение функции носит название _____________ функции |
18. | Впишите в утверждение нужный термин | Вектор первых частных производных функции многих переменных называется _____________ |
19. | Впишите в утверждение нужный термин | Матрица вторых частных производных функции нескольких переменных носит название матрицы ___________________. |
20. | Впишите в утверждение нужный термин | Множество точек, в которых функция f(x) принимает постоянное значение, называется линией _________________. |
21. | Впишите в утверждение нужный термин | Зависимость критерия оптимизации от параметров, влияющих на его значение, представленная в виде некоторой математической функции называется ___________ |
22. | Впишите в утверждение нужный термин | Стационарные точки, в которых функция не достигает ни минимума, ни максимума называются ___________________ |
23. | Установите правильную последовательность этапов решения оптимизационных задач: | · реализация задачи на ЭВМ; · определение количественного критерия; · выделение объекта; · выбор способа и метода оптимизации; · формализация задачи оптимизации; · анализ результатов; · формулировка проблемы; · построение математической модели объекта оптимизации. |
24. | Какое возможно количество решений в задаче оптимизации | · Одно · Два · бесконечное множество |
25. | 1. Метод золотого сечения 2. Метод множителей Лагранжа 3. Метод Нельдера-Мида | Установите соответствие между высказываниями, А. Метод многомерной безусловной оптимизации Б. Метод одномерной безусловной оптимизации В. Метод условной оптимизации |
Безусловная одномерная оптимизация | ||
26. | Унимодальной называется функция | · возрастающая; · убывающая; · выпуклая или вогнутая; · имеющая постоянное значение. |
27. | Чему соответствует нулевая производная функции в определенной точке | · Максимуму функции · минимуму функции · стационарной точке · точке экстремума |
28. | Какова связь между задачами минимизации и максимизации | · Равенство значений функции · Равенство значения аргументов · Противоположное значение функций |
29. | Как отличить стационарную точку функции от экстремума | · по знаку второй производной · по величине второй производной · по третьей производной |
30. | Какое количество экстремумов возможно в нелинейной целевой функции | a. одно b. два c. три d. бесконечное множество |
31. | Минимуму функции в точке экстремума соответствует | · f(x*) · - f(x*) · 0 |
32. | Минимуму функции -f(x) в точке x* соответствует условие: | · · · |
33. | Для точек x1 и x2 на отрезке унимодальности [a0 , b0] функции f(x) выполняется условие f(x1) > f(x2). Чему соответствует меньший отрезок [a1, b1] с точкой минимума x* | · a1 = a0 £ x* £x2 = b1 · a1 = x1 £ x* £ b0 = b1 · a1 = x1 £ x* £ x2 = b1 |
34. | В каком из методов одномерного поиска общее число вычислений функции для заданной точности требуется выбрать заранее | · метод половинного деления; · метод Фибоначчи; · метод золотого сечения; · метод локализации оптимума. |
35. | Расставьте методы одномерного поиска в порядке уменьшения числа расчетов целевой функции для определения экстремума с точностью e: | · золотого сечения; · равномерного поиска; · Фибоначчи; · половинного деления. |
36. | Сколько чисел Золотого сечения возникает в задаче одномерной оптимизации: | · одно · два · три |
37. | Что такое Число золотого сечения | · ½ · 0 · 1 · определяемая по другой формуле |
38. | Числа Золотого сечения подвержену закону: | · симметричны относительно середины интервала · Находятся в центре интервала · Находятся за пределами интервала |
39. | Укажите правильную последовательность реализации методов сокращения отрезка унимодальности: | · вычисление значений функции в двух точках внутри отрезка унимодальности; · определение нового отрезка; · выбор двух точек на начальном отрезке унимодальности; · проверка критерия останова алгоритма; · выбор начального отрезка унимодальности; · задание точности решения. |
40. | 1. Метод половинного деления 2. Метод квадратичной аппроксимации 3. Метод Ньютона | Установите соответствие между высказываниями, А. Метод точечного оценивания Б. Метод с ипользованием производных В. Метод последовательного сокращения отрезка унимодальности |
41. | От чего зависит количество чисел Фибоначчи, возникающее в задаче одномерной оптимизации: | · одно · два · три · от числа переменных · отчисла неизвестных |
42. | От чего зависит скорость поиска экстремума для многомерных функций | · вид целевой функции · задание начальной точки · от вида производной целевой функции · задание точности поиска экстремума · метода поиска |
43. | Чем обусловлено использование методов случайного поиска при одномерной оптимизации | · низкое число вычислений · возможность поиска глобальных экстремумом · независимость от выбора начальной точки |
44. | От чего зависит скорость поиска экстремума для одномерных функций | · вид целевой функции · задание начальной точки · задание точности поиска экстремума |
Безусловная многомерная оптимизация | ||
45. | Какие точки относятся к решению задач многомерной опримизации | · седловые · точки перегиба функции · точки минимума функции · точки максимума функции |
46. | Относятся ли седловые точки к решению задач безусловной оптимизации | · да · нет · не знаю |
47. | Расставьте в порядке значимости условия решения задачи многомерномерной оптимизации | · целевая функция · ограничения на решение целевой функции · наличие ограничений на диапазон независимых факторов · размерность задачи · наличие мощной вычислительной техники |
48. | 1. Метод Ньютона 2. Метод деформируемых многогранников 3. Метод наискорейшего спуска 4. Метод Гаусса-Зейделя | Установите соответствие между высказываниями, А. Симплексный алгоритм Б. Метод первого порядка В. Одномерный поиск вдоль направлений Г. Метод второго порядка |
49. | Симплексом в пространстве n переменных называется выпуклый многогранник, имеющий | · n+1 вершину; · n вершин; · n+2 вершины. |
50. | Положительно определенная матрица Гессе соответствует | · точке максимума функции; · седловой точке; · точке минимума функции. |
51. | Направленный случайный поиск требует задания | · целевой функции · производных значений |
52. | Выпуклая функция f определена в Rn, точка x является точкой минимума f на Rn. Выберите ситуацию, возможную при данном условии | · Проекция нуля на субдифференциал функции f в точке x есть направление наискорейшего возрастания f в данной точке · Проекция нуля на субдифференциал функции f в точке x есть направление наискорейшего убывания f в данной точке · Проекция нуля на субдифференциал функции f в точке x есть точка с неотрицательными компонентами |
53. | Для очередной итерации при поиске безусловного экстремума функции n переменных симплекс-методом требуется расчет функции | · в трех точках; · в двух точках; · в n точках; · в одной точке. |
54. | Если при отображении вершины симплекса в методе Нельдера-Мида значение функции в новой вершине оказалось наилучшим из всех производят | · редукцию симплекса; · сжатие симплекса; · растяжение симплекса; · следующее отображение. |
55. | Впишите в утверждение нужный термин | grad f(X) = 0 является ______________ условием экстремума функции |
56. | Впишите в утверждение нужный термин | Точка X*, в которой f(X*) = min f(X) при XÎRn является точкой _________ минимума функции |
57. | Впишите в утверждение нужный термин | Вектор, направленный в сторону противоположную вектору градиенту, называется ___________ |
58. | 1. Матрица 2. Матрица 3. Матрица | Установите соответствие между высказываниями, А. Отрицательно определена Б. Положительно определена В. Не относится ни к одной из упомянутых категорий |
59. | Для того чтобы функция была выпуклой необходимо и достаточно, чтобы главные миноры матрицы Гессе были… | · положительны · равны нулю · неотрицательны · равны двум · нет правильно ответа |
60. | Для того чтобы функция была вогнутой необходимо и достаточно, чтобы | · четные миноры ее гессианы были отрицательными, а нечетные положительными · нечетные миноры ее гессианы были отрицательными, а четные положительными · нечетные миноры ее гессианы равны нулю, а четные положительными · нечетные миноры ее гессианы были отрицательными, а четные равны нулю · нет правильного ответа |
61. | От чего зависит скорость поиска экстремума для многомерных функций | · вид целевой функции · задание начальной точки · от вида производной целевой функции · задание точности поиска экстремума · от размерности задачи · метода поиска |
62. | Если нечетные главные миноры гессианы отрицательны, а четные – положительные, то функция | · функция выпуклая; · функция вогнутая · функция линейная · функция квадратичная · нет правильного ответа |
Условная оптимизация. Нелинейное программирование | ||
63. | Что в нелинейном программировании называют допустимым решением? | · Любой вектор, удовлетворяющий системе ограничений задачи · Любой вектор, доставляющий целевой функции экстремальное значение · Любой вектор · Любой вектор, равный нулю · единичный вектор |
64. | Для методов нелинейного программирования характерны методы | · методы исключения переменных · прямые численные методы · метод множителей Лагранжа · методы оптимального управления |
65. | Что является главным для поиска решения задачи НП графическим методом | · выявление области определения факторов · построение множества допустимых решений · выявление узловых точек решения |
66. | Для задачи нелинейного программирования характерно | · нелинейная целевая функция · нелинейные ограничения · хотя бы одна нелинейная функция |
67. | Что из ниже перечисленного не относится к условиям оптимальности в математическом программировании? | · Графические условия оптимальности · Необходимые и достаточные условия оптимальности · Геометрические условия оптимальности · Условия Куна-Таккера · нет правильного ответа |
68. | Какую функцию в нелинейном программировании называют целевой функцией? | e. Любую нелинейную функцию, экстремум которой требуется найти f. линейную функцию g. Любую функцию h. только квадратичную функцию i. нет правильного ответа |
69. | Какое количество экстремумов возможно в нелинейной целевой функции и нелинейных ограничений | j. одно k. два l. три m. бесконечное множество |
70. | К нахождению седловых точек функции Лагранжа может быть сведена | n. любая задача оптимизации o. только классическая задача оптимизации p. зависит от начальных условий q. линейная задача r. транспортная задача |
71. | Условия Куна-Таккера определяют: | s. множители Лагранжа t. седловые точки функции Лагранжа u. взаимное влияние переменных v. решение задачи w. нет правильного ответа |
72. | Что определяет теорема Куна-Таккера | x. решение задачи y. седловую точку функции Лагранжа z. Экстремум функции Лагранжа |
73. | Что из ниже перечисленного относится к разделам нелинейного программирования? | · Целочисленное программирование · Динамическое программирование · Стохастическое программирование · Квадратичное программирование · нет правильного ответ |
74. | Что в нелинейном программировании называют допустимым решением? | · Любой вектор, удовлетворяющий системе ограничений задачи · Любой вектор, доставляющий целевой функции экстремальное значение · Любой вектор · значение множителей Лагранжа · координаты вершин многогранника |
75. | Каковы целевая функция и ограничения в задачах квадратичного программирования? | · Целевая функция - квадратичная, ограничения - линейны · Целевая функция - квадратичная, ограничения - квадратичны · Целевая функция - линейная, ограничения - квадратичны · Целевая функция - линейная, ограничения - линейны · Целевая функция – равны нулю, ограничения - линейны |
76. | К нахождению седловых точек функции Лагранжа может быть сведена | · любая задача оптимизации · только классическая задача оптимизации · зависит от начальных условий · линейная целевая функция · нет правильного ответа |
77. | Метод исключения позволяет решать задачи нелинейного программирования | · да · нет · в исключительных случаях |
78. | Задача квадратичного программирования относится к задачам | · линейного программирования · выпуклого программирования |
79. | Условия Куна-Таккера определяют необходимые условия | · оптимальности · максимума · минимума · равенства стратегий · минимума или максимума |
80. | Условия Куна-Таккера определяют седловую точку какой функции | · целевой функции · функции Лагранжа |
81. | Функция f, определенная в Rn, представляет собой функцию максимума из m гладких выпуклых в Rn функций. Выберите ситуацию, возможную при данном условии | · Функция f является гладкой и выпуклой · Функция f является выпуклой, но не гладкой · Функция f является гладкой, но не выпуклой |
82. | Функция f, определенная в Rn, представляет собой функцию максимума из m линейных в Rn функций. Выберите ситуацию, возможную при данном условии | · Функция f является выпуклой · Функция f не является непрерывной · Функция f не везде имеет субградиенты |
83. | Гладкая функция f выпукла в Rn. Точка x выбрана произвольно. Выберите ситуацию, возможную при данном условии | · Множество направлений спуска функции f в точке x состоит из одного элемента, а именно - антиградиента функции f в этой точке · Множество направлений спуска функции f в точке x есть открытое полупространство. Градиент функции f в точке x является нормалью к гиперплоскости, ограничивающей это полупространство. · Множество направлений спуска функции f в точке x состоит из конечного числа элементов |
84. | Функция f линейна в Rn. Выберите ситуацию, возможную при данном условии | · В любой точке х множество направлений спуска функции f не пусто · В любой точке х (кроме точки абсолютного минимума f в Rn) множество направлений спуска функции f не пусто · В любой точке х множество направлений спуска функции f пусто |
85. | Если все главные миноры гессианы неотрицальны, то | · функция выпуклая · функция вогнутая · функция линейная · функция квадратичная · нет правильного ответа |
86. | Непустое множество D из Rn, замкнуто, ограничено. Функция f выпукла на Rn. Выберите ситуацию, возможную при данном условии | · Функция f неограничена снизу на X. · Задача минимизации функции f на D не имеет допустимых решений. · Минимум функции f на Rn находится на границе множества D. |
87. | Функция f, определенная в Rn, n>2, представляет собой функцию максимума из конечного числа линейных функций. Выберите ситуацию, возможную при данном условии | · Для минимизации функции f в Rn можно применить методы линейного программирования · Для минимизации функции f в Rn можно применить субградиентный метод · Для минимизации функции f в Rn можно применить метод золотого сечения |
88. | Функция определенная в Rn, представляет собой функцию максимума из m выпуклых функций f1,..., fm. Выберите ситуацию, возможную при данном условии | · Лебегово множество функции f представляет собой пересечение лебеговых множеств функций f1,...,fm · Лебегово множество функции f никак не связано с лебеговыми множествами функций f1,...,fm. · Лебегово множество функции f пусто при любом значении константы |
89. | Гладкая функция f выпукла в Rn, точка x не является точкой минимума f на Rn. Выберите ситуацию, возможную при данном условии | · Антиградиент функции f в точке x является направлением убывания f в этой точке · Любое направление убывания f в точке x совпадает с антиградиентом в этой точке · Лебегово множество функции f для константы f(x) пусто |
90. | Функция f, определенная в Rn, n>2, представляет собой функцию максимума из конечного числа линейных функций. Выберите ситуацию, возможную при данном условии | · Для минимизации функции f в Rn можно применить методы линейного программирования · Для минимизации функции f в Rn можно применить субградиентный метод · Для минимизации функции f в Rn можно применить метод золотого сечения |
91. | Функция определенная в Rn, представляет собой функцию максимума из m выпуклых функций f1,..., fm. Выберите ситуацию, возможную при данном условии | · Лебегово множество функции f представляет собой пересечение лебеговых множеств функций f1,...,fm · Лебегово множество функции f никак не связано с лебеговыми множествами функций f1,...,fm. · Лебегово множество функции f пусто при любом значении константы |
92. | Гладкая функция f выпукла в Rn, точка x не является точкой минимума f на Rn. Выберите ситуацию, возможную при данном условии | · Антиградиент функции f в точке x является направлением убывания f в этой точке · Любое направление убывания f в точке x совпадает с антиградиентом в этой точке · Лебегово множество функции f для константы f(x) пусто |
93. | Непустое ограниченное множество D задано системой нестрогих линейных неравенств. Функция f выпукла на Rn. Выберите ситуацию, возможную при данном условии | · Функция f неограничена снизу на X. · Функция f достигает своего абсолютного минимума внутри X · Задача минимизации f на X не имеет решения. |
Модели и методы линейного программирования | ||
94. | Возможно ли решение задачи при несовместности решений | · да · нет · да, при задаче минимизации |
95. | Возможно ли решение задачи при неограниченности сверху | · нет · да · да, при задаче минимизации |
96. | Возможно ли решение задачи при неограниченности снизу | · нет · да · да, при задаче максимизации |
97. . | Какие переменные называют базисными? | · Переменные в системе ограничений задачи ЛП, которые определяют искусственный базис · Переменные, которые вводятся в систему ограничений задачи ЛП и преобразующие неравенства в равенства · Переменные, которые вводятся в целевую функцию · переменные, которые равны нулю · нет правильного ответа |
98. | Любая ли задача ЛП имеет конечное решение | · любая, · если нет зацикливания · если нет вырожденности · если базис решения равен 0 · нет правильного ответа |
99. | Как определяется ведущая строка при решении задачи ЛП симплекс-методом? | · Наименьшее число, расположенное в столбце тета симплекс-таблицы · Наибольшее число, расположенное в строке индексов симплекс-таблицы · Наименьшее число, расположенное в строке индексов симплекс-таблицы · Наибольшее число, расположенное в столбце тета симплекс-таблицы · нет правильного ответа |
100. | Как называется решение линейной задачи? | · Базисным решением · Полным базисным решением · Оптимальным решением · Точкой Куна-Таккера · нет правильного ответа |
101. | Можно ли любую задачу ЛП привести к каноническому виду? | · Нельзя · Можно, но не всегда · Можно · ЗЛП не приводится к каноническому виду · нет правильного ответа |
102. | Что из ниже перечисленного не входит в общую схему построения экономико-математической модели в ЛП | · Составление алгоритма решения задачи · Составление системы ограничений · Выбор критерия оптимальности · Выбор переменных · нет правильного ответа |
103. | Можно ли любую задачу ЛП решить симплекс-методом? | · Нет · Да · иногда · если базисные переменные равны 0 · нет правильного ответа |
104. | Как называют расширенную задачу в методе искусственного базиса? | · N - задачей · K - задачей · P - задачей · M - задачей |
105. | Что из ниже перечисленного не относится к свойствам задач ЛП? | · Множество планов любой задачи ЛП является выпуклым, если оно не пусто · Экстремальное значение целевая функция задачи принимает в одной из вершин многогранника решений · Экстремальное значение целевая функция задачи принимает в любой точке многогранника решений · любая игра имеет равновесие · нет верного ответа |
106. | Каким свойством обладает линия уровня в графическом методе решения задачи ЛП? | · Показывает направление убывания целевой функции · Целевая функция принимает постоянное значение для любой точки линии уровня · Показывает направление возрастания целевой функции · Целевая функция принимает нулевое значение · Целевая функция принимает только значение, большее нуля |
107. | Что в ЛП называют оптимальным планом? | · Произвольный набор чисел · Набор чисел, доставляющий экстремальное значение целевой функции · Набор чисел, удовлетворяющий системе ограничений задачи · Набор чисел, удовлетворяющий системе ограничений и доставляющий экстремальное значение целевой функции · вектор |
108. | Преобразование задачи к виду, допускающему симплексный алгоритм... | · требует аппроксимации · не требует аппроксимации · зависит от типа задачи · зависит от вида целевой функции · нет правильного ответа |
109. | Прямая называется опорной, если она | · не имеет общей точки с многоугольником · пересекает многоугольник · не пересекает многоугольник · имеет хотя бы одну общую точку с многоугольником и весь он лежит по одну сторону от нее · нет правильного ответа |
110. | При выполнении каких трех условий задача ЛП считается приведенной к каноническому виду? | · Требуется найти максимум целевой функции; б) система ограничений не содержит равенства; в) правые части системы ограничений неотрицательны · Требуется найти минимум целевой функции; б) система ограничений содержит только неравенства; в) правые части системы ограничений неотрицательны · Требуется найти максимум целевой функции; б) система ограничений содержит только равенства; в) правые части системы ограничений неотрицательны · Требуется найти максимум целевой функции; б) система ограничений содержит только равенства; в) левые части системы ограничений раны нулю · Требуется найти максимум целевой функции; б) система ограничений содержит только неравенства; в) правые части системы ограничений равны нулю |
111. | Назовите критерий оптимальности опорного плана в симплекс-метода решения задачи ЛП? | · Наличие положительных чисел в столбце тета симплекс-таблицы · Отрицательные значения оценок в строке индексов · Наличие отрицательных чисел в столбце тета симплекс-таблицы · Положительные значения оценок в строке индексов · нет правильного ответа |
112. | Как можно определить отсутствие конечного решения задачи ЛП при ее решении симплекс-методом? | · Отсутствие отрицательных чисел в ведущем столбце симплекс-таблицы · Отсутствие отрицательных чисел в строке индексов симплекс-таблицы · Отсутствие положительных чисел в ведущем столбце симплекс-таблицы · Отсутствие положительных чисел в строке индексов симплекс-таблицы · нет правильного ответа |
113. | Что называется планом в задаче ЛП? | · Набор чисел, доставляющий экстремальное значение целевой функции · Набор чисел, удовлетворяющий системе ограничений задачи · Произвольный набор чисел · двойственные оценки · нет правильного ответа |
114. | Что называют итерацией симплекс-метода? | · Приведение задачи ЛП к каноническому виду · Определение опорного плана задачи ЛП · Последовательное выполнение вычислений трех шагов симплекс-метода · Определение оптимального плана задачи ЛП · нет правильного ответа |
115. | В каком случае можно считать, что найдено решение ЗЛП на максимум симплексным методом | · если в строке целевой функции все элементы положительные · если в строке целевой функции все элементы отрицательные · если в строке целевой функции все элементы равны нулю · если в строке целевой функции все элементы положительные, либо равны нулю · нет правильного ответа |
116. | В каком случае можно считать, что найдено решение ЗЛП на минимум симплексным методом | · если в строке целевой функции все элементы положительные · если в строке целевой функции все элементы отрицательные, либо равные нулю · если в строке целевой функции все элементы равны нулю · если в строке целевой функции все элементы положительные, либо равны нулю · нет правильного ответа |
117. | Выберите верное утверждение | · ЗЛП имеет единственное решение · не существует допустимого решения ЗЛП · ЗЛП имеет много альтернативных решений · целевая функция ЗЛП неограниченна · ЗЛП не имеет двойственную задачу |
118. | Непустое множество D задано системой строгих линейных неравенств. Функция f линейна. Выберите ситуацию, возможную при данном условии | · Функция f неограничена снизу на X. · Функция f достигает своего абсолютного минимума внутри X. · Задача минимизации f на X не имеет решения |
119. | Непустое множество D задано системой нестрогих линейных неравенств. Функция f линейна. Выберите ситуацию, возможную при данном условии | · Функция f неограничена снизу на D. · Абсолютный минимум функции f находится внутри D. · Минимум функции f на множестве D совпадает с минимумом функции f на Rn |
120. | Задача линейного программирования имеет канонический вид. Множество допустимых решений непусто и ограничено. Выберите ситуацию, возможную при данном условии | · Оптимального решения задачи не существует · Дополнительные переменные составляют базис · Задача не имеет допустимого решения |
121. | Для решения задачи линейного программирования применяется симплексный метод. Выбран базис, состоящий из m векторов. Выберите ситуацию, возможную при данном условии | · На следующем шаге в базис введен еще один, (m+1)-ый по счету вектор · Один из дополнительных столбцов был выведен из базиса, а через несколько шагов снова введен в него · В оптимальном плане число ненулевых компонент превышает число базисных элементов |
122. | Задача линейного программирования не имеет допустимых решений. Выберите ситуацию, возможную при данном условии | · Приведением к каноническому виду можно добиться непустоты допустимого множества · Примененяя метод искусственного базиса можно найти оптимальный опорный план · В базисе опорного плана, отвечающего критерию оптимальности, присутствуют искусственные переменные |
123. | В канонической форме задачи линейного программирования число переменных n и ограничений m должно находиться в соотношении | · n > m; · n = m; · n < m. |
124. | Решение задачи линейного программирования (если оно единственно) находится: | · внутри области ограничений; · на одном из ребер многогранника ограничений; · в одной из вершин многогранника ограничений. |
125. | Что из ниже сформулированного не имеет никакого отношения к основной теореме двойственности? | · Экстремальные значения целевых функций двойственных задач совпадают · Если одна из двойственных задач ЛП имеет решение, то имеет решение и другая задача · Положительную двойственную оценку могут иметь лишь ресурсы, полностью используемые в оптимальном плане · решения двойственных задач совпадают · решения двойственных задач не совпадают |
126. | Что дает решение двойственной задачи ЛП использования сырья? | · Оптимальный план использования сырья · Оптимальный план выпуска продукции · Оптимальную систему оценок использования сырья · теневую цену продукции · нет правильного ответа |
127. | В каком случае двойственная оценка в задаче распределения ресурсов равна нулю? | · Данный ресурс не полностью используется в оптимальном плане · Данный ресурс полностью используется в оптимальном плане · Когда производство данной продукции убыточно · Когда производство данной продукции по двойственным оценкам оправдано · нет правильного ответа |
128. | В каком случае двойственная оценка в задаче распределения ресурсов больше нуля? | · Когда соответствующий ресурс полностью используется в оптимальном плане · Когда соответствующий ресурс не полностью используется в оптимальном плане · Когда по двойственным оценкам производство продукции не убыточно · когда продукция не выпускается · нет правильного ответа |
129. | Если одна из симметричных взаимодвойственных задач имеет решение, то | · Не имеет решение и другая · имеет решение и другая · решение другой - пустое множество · решение другой не зависит от решения исходной задачи · нет правильного ответа |
130. | Выберите верное утверждение | · задача, двойственная к двойственной, совпадает с исходной прямой задачей · если одна из двойственных задач имеет решение, то в другой нет решения · если в прямой задаче есть ограничение в виде равенства, то соответствующая переменная двойственная задачи обязательно будет свободной · свободная переменная прямой задачи порождает в двойственной задаче ограничение в виде равенства · если в прямой задаче ограничения имеют знак ≥, то в двойственной ограничения имеют ≤. |
131. | К задаче линейного программирования поставлена двойственная задача. Выберите ситуацию, возможную при данном условии | · Оптимальное значение целевой функции прямой задачи больше, чем оптимальное значение целевой функции двойственной задачи · Оптимальные планы прямой и двойственной задач различны · Оптимальные значения целевых функций планы прямой и двойственной задач достигаются в одной и той же точке |
Специальные задачи линейного программирования | ||
132. | Задача о назначениях относится | · к параметрическим задачам линейного программирования · к целочисленным задачам линейного программирования · к нелинейным задачам |
133. | К каким видам игр относятся стратегические игры? | · К непрерывным · К дискретным · К комбинаторным · биматричным · с нулевой суммой |
134. | Какое из утверждений верно? а (нижняя цена игры) и b (верхняя цена игры) | · а<=b · a>=b · это зависит от матрицы · вообще неверно · нет верного утверждения |
135. | Найдите неверное утверждение | · решение называется допустимым, если оно удовлетворяет набору определенных условий · признак предпочтения называется критерием оптимальности · Нэш доказал, что любая бескоалиционная игра имеет хотя бы два равновесия · целевая функция – это количественный показатель предпочтительности · решение называется оптимальным, если оно допустимо |
136. | Оптимальной стратегией называется | · стратегия, которая определяет максимум ожидаемого среднего выигрыша при многократном повторении игры · стратегия, которая определяет минимум ожидаемого среднего выигрыша при многократном повторении игры · стратегия, которая определяет средний выигрыш при многократном повторении игры · стратегия, которая равна нулю · нет правильного ответа |
137. | Математическое описание конфликтной ситуации называется | · игрой · задачей линейного программирования · конфликтом · стратегией · Седловой точкой |
138. | Какие встречаются типы игр? | · кооперативные, некооперативные · биматричные · с нулевой и ненулевой суммой · матричные · все выше перечисленные |
139. | Если выигрыш одного игрока равен проигрышу другого, то эта игра называется | · игрой с нулевой суммой · кооперативной игрой · бескоалиционной игрой · биматричной игрой · все выше перечисленное верно |
140. | Если до начала игры игроки образуют коалиции, то эта игра называется | · игрой с нулевой суммой · кооперативной игрой · бескоалиционной игрой · биматричной игрой · все выше перечисленное верно |
141. | Игра, в которой игроки не могут координировать свои действия называется | · игрой с нулевой суммой · кооперативной игрой · бескоалиционной игрой · биматричной игрой · все выше перечисленное верно |
142. | Если верхняя цена игры равна нижней, то эта игра имеет | · максминую стратегию · минимаксную стратегию · седловую точку · не имеет решения · нет правильного ответа |
143. | С каким из утверждений не следует согласиться | · бескоалиционная игра-это игра, моделируемая в предположении, что игроки неспособны заключать принудительные соглашения · кооперативная игра – это игра, моделируемая в предположении, что игроки способны заключать принудительные соглашения · Нэш доказал, что каждая конечная игра имеет по крайней мере два равновесия · игра является полной информацией, если все игроки знают характер игры в смысле знания развернутой формы игры · игра с неполной информацией игроки не обладают полнотой сведений |
144. | Транспортная задача является замкнутой. Выберите ситуацию, возможную при данном условии | · Существует оптимальное решение задачи · Оптимального решения задачи не существует · Задача не имеет допустимого решения |
145. | Впишите в утверждение нужный термин | Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, то модель такой транспортной задачи называется_____________ типа |
146. | В каком случае транспортную задачу называют классической? | · При наличииограничений · Сбалансированную задачу · Несбалансированную задачу |
147. | Может ли МДР транспортной задачи быть пустым? | · да · нет · не знаю |
148. | Как связаны между собой задача о назначениях и классическая транспортная задача | · транспортной матрицей · целевой функцией · набором переменных · дополнительными ограничениями |
Динамическое программирование | ||
149. | Что из ниже перечисленного относится к недостаткам метода динамического программирования? | · Допускает применение компьютеров для решения задач · Позволяет упростить поиск оптимальных решений · Отсутствие универсального алгоритма · Трудоемкость решения · Нет правильного ответа |
150. | Какие задачи можно решать с помощью метода динамического программирования? | · Многошаговые · Одношаговые · Линейные · Нелинейные · нет правильного ответа |
151. | Что лежит в основе концепции метода динамического программирования? | · Принцип максимума Понтрягина · Принцип оптимизации Беллмана · Метод Лагранжа · Теорема Куна-Таккера · нет правильного огвета |
152. | Какому условию должна удовлетворять задача динамического программирования? | · Условие аддитивности целевой функции · Условие отсутствия последействия · Условие Куна-Таккера · условия Седловой точки · условие равенства двойственных оценок |
153. | В чем состоит принцип оптимальности Беллмана для задач динамического программирования? | · Решение на каждом следующем шаге должно приниматься без учета результатов предыдущих шагов · Решение на каждом следующем шаге должно приниматься с учетом результата, полученного на всех предыдущих шагах · Решение на каждом следующем шаге должно приниматься с учетом результата, полученного только на предыдущем шаге · решение принимается в зависимости от вида целевой функции · решение принимается, если равно нулю предыдущее |
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
САМОСТОЯТЕЛЬНОЙ РАБОТЫ
№ | Тема для самостоятельного изучения | час |
1 | Введение в исследование операций. Основы классической теории оптимизации Понятие операции. Цель и задачи исследования операций. Примеры задач исследования операций. Место дисциплины исследования операций среди смежных дисциплин. Введение в классическую теорию оптимизации. Основные понятия и определения: задача оптимизации, виды критериев и их свойства, оптимальное решение. Постановка задачи оптимизации. Типы оптимальных решений. Графическое решение. Понятие градиента и его геометрическая интерпретация. Множество допустимых решений. Этапы исследования операций. Классификация методов исследования операций. Типовые постановки задач, их геометрическая интерпретация и методы решения. | 7 |
2 | Безусловная одномерная оптимизация Аналитический и графический анализ функции. Необходимые и достаточные условия экстремума. Процесс численного нахождения оптимального решения. Начальное приближение. Контроль точности. Классификация численных методов. Поисковые методы точечного оценивания: метод обратного переменного шага, квадратичной аппроксимации, метод Пауэлла. Методы последовательного сокращения отрезка неопределенности: равномерный поиск, метод локализации оптимума, половинного деления, золотого сечения, Фибоначчи. Сравнительный анализ одномерных методов сужения интервала. | 7 |
3 | Безусловная многомерная оптимизация Аналитический и графический анализ функции. Общая идея численных методов. Методы оценки точности решения. Классификация численных методов. Поисковые методы переборного типа: сканирования с равномерным и переменным шагом. Методы на основе пошаговой одномерной оптимизации: поочередного изменения переменных, Гаусса- Зейделя, Хука-Дживса. Симплексные алгоритмы: обычный симплекс-метод, метод Нелдера-Мида. Методы случайного поиска: ненаправленный случайный поиск, метод случайных направлений. Многомерные методы оптимизации с использованием производных: градиентный, наискорейшего спуска (крутого восхождения). Сравнительный анализ многомерных методов оптимизации. | 7 |
4 | Модели и методы линейного программирования Постановка и особенности задач условной оптимизации. Классификация и характеристика методов решения. Линейное программирование. Примеры построения линейных оптимизационных моделей: оптимальная смесь, оптимизация плана производства, распределение ресурсов, загрузка оборудования и др. Геометрическая интерпретация и графический метод решения. Графический анализ устойчивости решения задачи линейного программирования. Каноническая форма задачи. Методы решения задач линейного программирования. Теоретическая основа симплекс-метода и алгоритм его реализации. Постановка и решение двойственной задачи линейного программирования. Двойственный симплекс-метод. | 7 |
5 | Специальные задачи линейного программирования Целочисленная задача линейного программирования. Методы отсечения. Метод Гомори. Понятие о методе ветвей и границ. Постановка и методы решения транспортной задачи. Закрытая и открытая модель транспортной задачи. Задача о назначениях и выбора кратчайшего пути. Задача коммивояжера. Элементы теории игр. Основные понятия, классификация и описание игр. Матричные игры и понятие седловой точки. Смешанные стратегии. Решение матричных игр методами линейного программирования и графическим способом. | 7 |
6 | Условная оптимизация. Нелинейное программирование Постановка задачи и ее анализ. Выпуклое множество. Выпуклая и вогнутая функции. Выпуклая задача оптимизации. Классификация задач и методов нелинейного программирования. Постановка и геометрическая интерпретация задачи. Графический метод решения для функции двух переменных. Классические методы решения с ограничениями типа равенств: метод исключения, метод множителей Лагранжа. Неклассические методы решения с ограничениями типа неравенств. Необходимые и достаточные условия Куна - Таккера для условного экстремума. Выпуклая задача квадратичной оптимизации. Постановка и методы решения задачи квадратичного программирования. Поисковые методы решения задач нелинейного программирования: линейной аппроксимации, "скользящего" допуска, возможных направлений, штрафных и барьерных функций. | 7 |
7 | Динамическое программирование Общая схема методов динамического программирования. Примеры задач динамического программирования. Принцип оптимальности и уравнение Беллмана. Задача о распределении средств между предприятиями. Общая схема применения метода динамического программирования. Задача о замене оборудования. | 7 |
8 | Специальные модели исследования операций Модели сетевого планирования и управления. Основные элементы сетевой модели. Порядок и правила построения сетевых графиков. Упорядочение и оптимизация сетевого графика. Модели управления запасами. Статические детерминированные модели. Управление запасами при случайном спросе и предложении. | 73 |
ТЕМЫ РЕФЕРАТОВ
1. Метод Розенброка для задачи безусловной оптимизации.
2. Безусловная оптимизация методом сопряженных направлений.
3. Метод случайных направлений поиска безусловного экстремума.
4. Метод наискорейшего спуска.
5. Метод безусловной оптимизации Ньютона-Рафсона.
6. Определение начального базисного решения задачи линейного программирования методом штрафов (М - метод).
7. Общая и двойственная задача линейного программирования.
8. Решение задачи линейного программирования двухфазным симплекс-методом.
9. Целочисленная задача линейного программирования (метод Гомори – отсекающих плоскостей).
10. Целочисленная задача линейного программирования (метод ветвей и границ).
11. Решение задачи коммивояжера.
12. Транспортная задача (метод северо-западного угла).
13. Транспортная задача (метод минимального элемента).
14. Транспортная задача (улучшение плана - метод потенциалов).
15. Задача о кратчайшем пути (метод Фогеля).
16. Задача о кратчайшем пути (Метод Минти).
17. Задача о назначениях (венгерский метод).
18. Решение задачи нелинейного прогр. методом множителей Лагранжа.
19. Метод проекции градиента для задачи условной оптимизации.
20. Метод возможных направлений Зойтендейка для решения задачи нелинейного программирования.
21. Случайный поиск (метод Монте-Карло) при наличии ограничений.
22. Графический метод решения задачи условной оптимизации.
23. Нелинейная распределительная задача (динамическое программирование).
24. Задача об инвестировании предприятий (динамическое программирование).
25. Задача о замене оборудования (динамическое программирование).
26. Задача о найме работников (динамическое программирование).
27. Задача управления запасами без дефицита.
28. Задача управления запасами с дефицитом.
29. Задача управления запасами при случайном спросе.
30. Задача оптимизации порядка обслуживания требований.
31. Задача о максимальном потоке (метод Форда и Фалкерсона).
32. Задача о кратчайшем пути (алгоритм Дейкстры).
33. Расчет детерминированного сетевого графика (метод критического пути).
34. Расчет вероятностного сетевого графика.
35. Игры двух лиц с нулевой суммой.
36. Игры двух лиц с ненулевой суммой (кооперативные игры).
37. Выбор оптимальной стратегии в условиях неопределенности.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Введение в исследование операций. Основы классической теории оптимизации
1. Цель, задачи и методы исследования операций.
2. Исследование операций и ее место среди других наук.
3. Основные понятия и определения теории оптимизации.
4. Общая классификация методов скалярной оптимизации.
5. Основные этапы решения задач оптимизации.
6. Множество допустимых решений. Понятие выпуклых множеств и выпуклых функций
Безусловная одномерная оптимизация
7. Необходимые и достаточные условия экстремума функции одной переменной.
8. Классификация численных методов одномерной оптимизации. Методы сканирования и локализации оптимума.
9. Общая схема сужения промежутка унимодальности для одномерной функции. Методы половинного деления, золотого сечения и Фибоначчи.
10. Методы точечного оценивания экстремума одномерной функции. Метод обратного переменного шага, квадратичной аппроксимации, Пауэлла.
Безусловная многомерная оптимизация
11. Необходимые и достаточные условия экстремума функции нескольких переменных.
12. Классификация численных методов многомерной оптимизации. Методы сканирования и локализации оптимума.
13. Методы покоординатного поиска экстремума функции нескольких переменных.
14. Метод Хука и Дживса.
15. Симплекс - метод поиска экстремума функции нескольких переменных.
16. Метод деформируемых многогранников Нельдера - Мида.
17. Обычные градиентные методы.
18. Методы наискорейшего спуска (крутого восхождения).
19. Методы случайного поиска экстремума.
20. Сравнительный анализ численных методов многомерной оптимизации.
Условная оптимизация. Нелинейное программирование
21. Постановка задачи и классификация методов статической условной оптимизации.
22. Постановка и методы решения задачи нелинейного программирования. Ее геометрическая и экономическая интерпретации.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 |




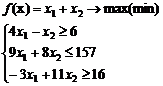 является задачей
является задачей