Множество граничных узлов состоит из точек пересечения прямых , проходящих через все внутренние узлы с границей Множества , , граничных по направлениям узлов состоят из точек пересечения прямых , соответственно с границей области

В каждом узле сетки рассчитываем значение дозы по формуле

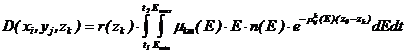, (1)

где - линейный коэффициент ослабления, зависящий от материала слоя в точке ; - поправочный коэффициент, определяющий рассеяние и взаимное проникновение электроном на границе двух областей; - массовый коэффициент передачи энергии для квантов с энергией ; - функция, описывающая распределение квантов по спектру энергии от до .

Далее, в соответствии с динамическим рассмотрением задачи, выбирается шаг квантования по времени . Для каждого момента времени , рассчитывается распределение температуры и напряжения растяжения-сжатия.

Проведя расчеты указанным образом, будем иметь распределение температуры и напряжений в каждый момент времени с начала воздействия импульса ().

Для определения поля температур введем обозначения: – теплоемкость в точке , , - плотность материала с координатой , , 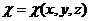- коэффициент теплопроводности в точке , , 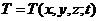– температура в точке в момент времени .

Рассмотрим вначале процесс мгновенного разогрева. Изменение температуры в каждой точке области происходит лишь за счет поглощения энергии излучения и описывается уравнением

,, (2)

где 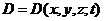- доза, полученная каждым слоем. С учетом начального условия

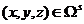, , (3)

получим задачу Коши, которая решается аналитически и ее решение имеет вид

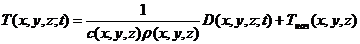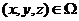, (4)

Необходимо определить значение температуры в момент времени, когда действие импульса прекращается:

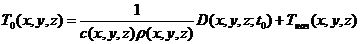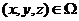, (5)

Функция описывает распределение температуры в структуре изделия непосредственно после действия импульса. Значение дозы 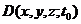рассчитывается в узлах сетки по формуле.

Далее действие внешнего источника прекращается и в течение некоторого времени происходит перераспределение температуры, которое в области описывается уравнением теплопроводности с переменными коэффициентами

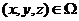, , (6)

Поскольку значение мало, для удобства вычислений можем считать за начальное время .

Значение температуры в начальный момент времени определяется на предыдущем этапе и вычисляется по формуле

(7)

На границе области происходит теплообмен с окружающей средой, который описывается граничными условиями третьего рода

(8)

И поскольку область неоднородна, то на границах раздела подобластей должны выполняться условия сопряжения

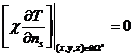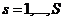, (9)

где - граница области , - граница подобласти , - коэффициент теплопереноса, - температура среды, - нормаль к границе , - нормаль к границе , - скачок функции при переходе через границу .

Таким образом, получена краевая задача для уравнения теплопроводности в области . Перераспределение тепла происходит в течение некоторого времени , по истечении которого температура корпуса и кристалла сравнивается с температурой окружающей среды. Момент времени прогнозируется и обычно составляет 1000 секунд. Таким образом, мы приходим к математической задаче:

В цилиндре требуется найти непрерывную функцию где удовлетворяющую уравнению

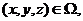
(10)

начальному условию

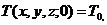
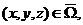(11)

граничному условию

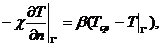(12)

и условиям сопряжения на границах раздела структурных слоев

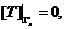
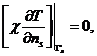(13)

Для решения данной задачи предложен метод суммарной аппроксимации, который позволяет рассчитать значения температуры в узлах трехмерной сетки с определенным шагом квантования по времени. Тогда определение температуры определяется решением последовательностью одномерных уравнений

при (14)

при (15)

при (16)

,

с условиями

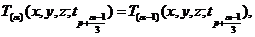
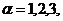
(17)

где , , 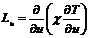, 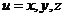- шаг квантования по времени.

Изложенный подход позволяет определить динамику изменения температур и оценить время потери работоспособности вследствие превышения температурой активных элементов кристалла предельно-допустимых значений по ТУ.

Термомеханические напряжения, возникающие в изделии в результате импульсного разогрева, представляют собой сжатие материалов, которое в свою очередь приводит к генерации волн напряжения по материалам конструкции в виде растяжения-сжатия. Таким образом, импульсные термомеханические напряжения можно разделить на две фазы:

1. Напряжение сжатия, возникающее в первый момент, непосредственно после импульса рентгеновского излучения, которое описывается формулой:

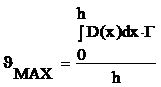, (18)

где Г - коэффициент Грюнайзена; h - толщина слоя; х – координата; D(x) – доза в точке с координатой х.

2. Распространение волн растяжения-сжатия по материалам конструкции с их последующей интерференцией описывается выражением:

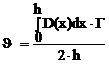. (19)

Прочность материалов каждого слоя определяется интерференцией волн растяжения:

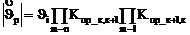; , (20)

где р - слой, в котором подсчитывается величина упругих напряжений; m - число слоев; к - порядковый номер слоя; l - число слоев от p-го слоя до свободной границы с одной стороны; n - число слоев от p-го слоя до свободной границы со второй стороны; Kпр - коэффициенты прохождения волны напряжения из i-го в k-й слой, определяемые по выражению

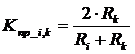, (21)

где r - плотность; Vзв - скорость звука.

Kотр - коэффициенты отражения между i-м и k-м слоем, определяемые по выражению

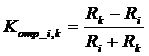. (22)

Помимо термомеханического удара наблюдаются напряжения, возникающие вследствие расширения конструктивных элементов от выделившегося в них тепла. При классическом подходе эти явления рассматривались без учета габаритных размеров конструкции, а оценка напряжения проводилась в момент времени непосредственно после воздействия импульса.

В настоящей работе предложена модель, которая позволяет учесть габаритные размеры конструкции изделия, а оценку напряжений производить в момент времени, при котором эти напряжения достигают максимального значения.

Задача расчета термомеханических напряжений в трехмерной области включает в себя три уравнения равновесия

, (23)

, (24)

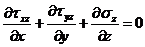, (25)

шесть уравнений совместности деформаций

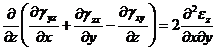, , (26)

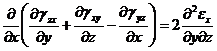, , (27)

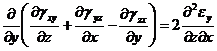, , (28)

шесть уравнений обобщенного закона Гука в прямой

, , (29)

, , (30)

, (31)

или в обратной форме

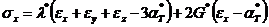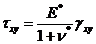, , (32)

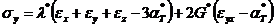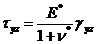, , (33)

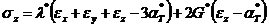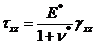, , (34)

где 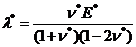- коэффициент Ляме, - модуль сдвига, 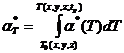- температурный коэффициент расширения.

На нижней части поверхности выполняются кинематические граничные условия в перемещениях

, , , (35)

а на остальных частях поверхности задаются статические граничные условия в напряжениях

, (36)

, (37)

, (38)

где ,,,,, - компоненты тензора напряжений; ,,,,,- компоненты тензора деформаций; ,, - перемещения по , и соответственно; ,, - направляющие косинусы нормали к поверхности ; - модуль Юнга; - коэффициент Пуассона; - коэффициент Ляме; - модуль сдвига; 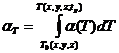- температурный коэффициент расширения.

На основе данного подхода получаем задачу расчета термомеханических напряжений представляет собой квазистатическую задачу термоупругости в трехмерной многосвязной области.

Для решения этой задачи рассматриваемая конструкция представляется как кусочно-однородное тело, т. е. тело, состоящее из отдельных частей с различными, но постоянными в пределах каждой из них, физико-механическими характеристиками. В качестве начального распределения температуры используется полученное при расчете тепловых эффектов динамическое поле температур.

Стойкость к рентгеновскому излучению по тепловым и термомеханическим эффектам определяется с помощью нахождения максимальных уровней рентгеновского излучения при которых не происходит катастрофических отказов. При необходимости рассчитывается время потери работоспособности изделия из-за перегрева кристалла.

В четвертом разделе описаны предложенные математические модели переходных радиационных процессах в типовых элементах микросхем при воздействии импульсного ионизирующего излучения.

Вначале рассчитывается мощность дозы ионизирующего излучения, которая в общем случае может быть определена по предложенной формуле:

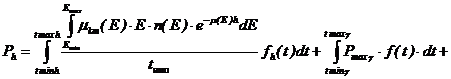
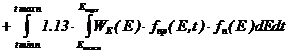(39)

В данном выражении времена tmin и tmax относятся к рентгеновскому, гамма - и нейтронному излучению. Так tminh – время, когда начинается действие рентгеновского излучения, tmaxh – время окончания действия рентгеновского излучения; tminγ – время, когда начинается действие гамма-излучения, tmax – время окончания действия гамма-излучения; tminn – время, когда начинается действие нейтронного излучения, tmaxn – время окончания действия нейтронного излучения.

Для прогнозировании величины тока ионизации предложены математические модели, учитывающие спектрально-энергетические и амплитудно-временные характеристики импульса, технологические особенности изготовления и температурный режим.

Для одиночного прямоугольного импульса ионизирующего излучения с учетом периферийных областей ионизационный ток p–n перехода можно записать в следующем виде:

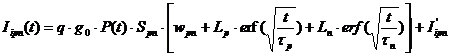(40)

где - составляющая ионизационного тока от периферийных областей p-n перехода, определяющаяся выражением:

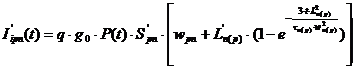(41)

При условии малых размеров периферийных областей, ионизационный ток периферийной области зависит от диффузионной длины неосновных носителей заряда с внешней стороны перехода и будет выглядеть следующим образом. 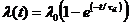где τiλ – при уменьшении толщины области полупроводника будет равняться .

Выражение для зависимости ионизационного тока от температуры примет следующий вид:

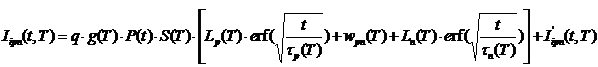, (42)

где составляющая ионизационного тока, учитывающая уменьшение размеров активных областей элементов, будет выглядеть:

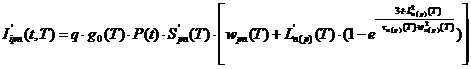(43)

Величина ионизационного тока в зависимости от мощности дозы для реального импульса ИИ может быть получена путем разложения сложной формы импульса излучения на суперпозицию N прямоугольных импульсов.

Для каждого i-го прямоугольного импульса вычисляется функция изменения ионизационного тока Iipn во времени. Суммарный ионизационный ток равен

(44)

где - d(t-ti) – дельта-функция; ti – шаг разбиения реального импульса на совокупность прямоугольных импульсов; t – длительность импульса по времени.

Выражения для токов ионизации подставляются в виде генераторов токов в средства схемотехнического моделирования при этом импульс генератора тока задается с применением экспоненциальной функции EXP (y1, y2, td, tcr, tr, tfr) и описывается выражением:

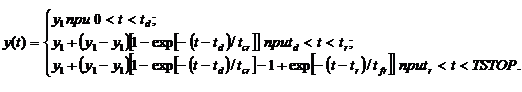(45)

Для проектирования СБИС с малыми проектными нормами предложено использовать короткоканальную модель, которая по сравнению с ранее существующими моделями позволяет учитывать следующие особенности: зависимость подвижности носителей от вертикального поля; распределение заряда обедненной области между стоком и истоком; неоднородность легирования для транзисторов, изготовленных с применением ионной имплантации; модуляция длины канала; зависимость всех параметров от геометрии транзистора.

В режиме сильной инверсии пороговое напряжение определяется

(46)

Параметры К1, К2 моделируют неоднородность легирования, где К1 подобен параметру GAMMA в модели первого уровня, VFB частично моделирует уменьшение длины канала.

Ток стока в режиме сильной инверсии определяется соотношениями:

В режиме отсечки

В линейном режиме

На основе схемотехнического моделирования создается библиотека моделей элементов, которые учитывают ионизационное излучение. Условно такие элементы можно считать «неисправными». При переходе из схемотехнического базиса в функционально-логический необходимо каждому «неисправному» элементу на схемотехническом уровне поставить в соответствие «неисправный» элемент на функционально-логическом уровне. Однако, число этих элементов достаточно велико. Так как одному исправному элементу необходимо поставить в соответствие множество «неисправных», число элементов которого зависит от мощности дозы, длительности импульса, температуры.

Для сокращения вычислительных затрат и уменьшения объема памяти предложены аппроксимационные соотношения, позволяющие провести пересчет времени потери работоспособности каждого элемента для любой мощности дозы, длительности импульса и температура по известным 4 значениям полученных при различных уровнях мощности дозы, длительности и температуры.

В пятом разделе описано моделирование дозовых эффектов. Разработаны математические модели, которые позволяют более адекватно учитывать радиационные эффекты с учетом конструктивно-технологических параметров и характеристик внешних воздействующих факторов в соответствии с КГС «Климат-7».

Для универсальности подхода автором предложено сведения всех видов радиационного воздействия (электроны, протоны или гамма-кванты) - к единому фактору - ионизационной составляющей поглощенной дозы.

Предложены соотношения для определения радиационно-индуцированного накопления заряда в подзатворном диэлектрике МОП-структуры. Для решения данной задачи используется квазистационарное приближение, т. е. неизменность распределения концентрации свободных дырок по толщине SiO2 во время радиационного облучения , где р — концентрация свободных дырок в объеме SiO2. Накопление заряда определяется соотношением

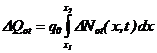(47)

где q0 — элементарный заряд; Not(x, t) — распределение концентрации заряженных E’-центров по толщине оксида в момент времени t.

Величина Not(x, t) может быть определена из соотношения

=
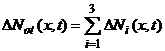. (48)

где; A(x,0) — концентрация неравновесных состояний; n(x, t) — распределение свободных электронов по толщине оксида в момент времени t; Kрел – количество напряженных связей, релаксирующих при одном разрыве; р(x) — распределение свободных протонов по толщине оксида в момент времени t; k1, k2, k2 - константы; NSiOH — распределение комплексов ºSi–OH по толщине подзатворного диоксида кремния.

Для расчета концентрации свободных протонов и дырок используется система уравнений

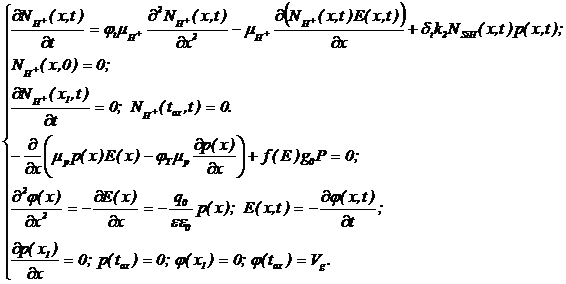(49)

где 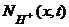— распределение концентрации протонов по толщине оксида в момент времени t; mН+ — подвижность протонов в SiO2; — константа; ; E(x, t) — распределение напряженности электрического поля в SiO2, NSiH — распределение комплексов ºSi–H по толщине подзатворного диоксида кремния; f(Eox) - выход заряда, который определяется как доля дырок, избежавших начальной рекомбинации и является функцией от электрического поля в оксиде, mр — подвижность дырок в SiO2; jТ = kT / q0 — тепловой потенциалe0 = 8,85×10–14 Ф/см — диэлектрическая константа;; e — относительная диэлектрическая проницаемость оксида, P – мощность дозы, g0 — эффективность ионизации; .

Для высокой мощности дозы и низкоинтенсивного излучения моделирование расчет накопления заряда в диэлектрике сводится к решению следующей системы:



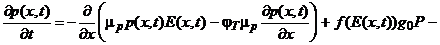
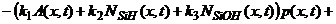
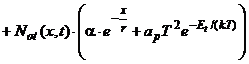; (50)

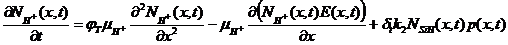; (51)

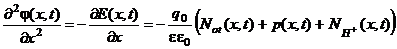; (52)

; (53)

; (54)

; (55)

; (56)


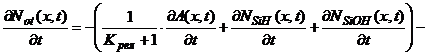
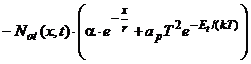; (57)

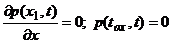; ; (58)

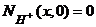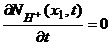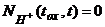; ; ; (59)

, (60)

где mр — подвижность дырок в SiO2; jТ = kT / q0 — тепловой потенциал; mН+ — подвижность протонов в SiO2; — распределение концентрации протонов по толщине оксида в момент времени t; e0 = 8,85×10–14 Ф/см — диэлектрическая константа; q0 — элементарный заряд; e — относительная диэлектрическая проницаемость оксида, 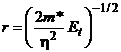; a — частота попыток вылета электронов через потенциальный барьер; m* — эффективная масса электрона внутри барьера; Et — энергетический уровень ловушки (для типовых значений глубины залегания ловушек в запрещенной зоне диоксида значения параметров, можно оценить как a »5∙1012 с–1; r » 0,1–0,2 нм); ap — константа, зависящая от сечения захвата ловушки, для которой можно записать .

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3