УДК 621.372
ЭЛЕМЕНТЫ МАТЕМАТИКИ ГАРМОНИИ
В ТЕОРИИ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Н. Ф. СЕМЕНЮТА
канд. техн. наук, профессор
академик Международной академии связи
почетный профессор
Белорусский государственный университет транспорта (г. Гомель)
Математика гармонии в последние годы получила применение в науке, технике, образовании. Так, в учебных пособиях для студентов[1, 3] изложены проявления элементов математики гармонии в природе и искусстве, в [2, 4] – науке и технике. В 2009 г. в издательстве «Наука мира» в Сингапуре был издан обобщенный труд «Математика гармонии – от Евклида до современной математики» [5]. В 2011 г. на базе Одесского национального университета был проведен 1-й Конгресс по математике гармонии, где были обсуждены достижения в этом новом направлении математики, намечены пути дальнейшего развития математики гармонии в различных областях искусства, науки, техники и образования, в том числе теории линейных электрических цепей.
В настоящее время теория гармонии развивается и оказывает большое вияние на методы исследования и способы решеня многих практических и теоретических задач в самых разнообразных областях науки и техники, искусства, музыки, живописи, поэзии, архитектуры, биологии, медицини, вычислительной технике, экономике, социологии и др. Математика гармонии носит поистинно трансдисциплинарный, общеобразовательный характер и составляет элемент культуры всякого образованного человека, каков бы не был профиль его профессиональной подготовки.
Целью настоящей статьи является обобщение работ автора по применению рекуррентных последовательностей к анализу однородных электрических цепей [2, 4]. Предложенный автором метод анализа значительно сокращает трудоемкость и время на расчеты лестничных цепей по сравнению с известными методами (законы Ома и Кирхгофа, контурные уравнения токов и узловых напряжений и др.). Метод позволяет по-новому также подойти к решению многих теоретических и практических задач в науке и технике, теории электрических цепей (ТЛЭЦ) и др.
Метод, основанный на математике гармонии, назван автором методом лестничных чисел [2]. В основу метода положены рекуррентные (Фибоначчи, Люка и др.) и мультирекуррентные последовательности чисел.
![]() Мультирекуррентные последовательности чисел формируются соотношениями:
Мультирекуррентные последовательности чисел формируются соотношениями:
![]() S2n = S2n-1 + S2n-2;
S2n = S2n-1 + S2n-2;
S2n-1 = kS2n-2 + S2n-3, (1)
где S1 = 1, S2 = 1, k – параметр последовательности.
Четные S2n и нечетные S2n-1 члены последовательности (1) определяются суммированием двух предыдущих чисел. Однако числа с четными номерами перед суммирование умножаются на коэффициент k. Следовательно, последовательность (1) является мультирекуррентной.
Числа мультирекуррентнх последовательности (1) можно представить в виде многочленов
S1 = 1, S5 = k2 + 3k2 + 1,
S2 = 1, S6 = k2 + 4k2 + 3,
S3 = k + 1, S7 = k3 + 5k2 + 6k +1,
S4 = k + 2 , S8 = k3 + 6 k2 + 10k + 4.
Коэффициенты многочленов совпадают с биноминальными коэффициентами треугольника Паскаля. Следовательно, мультирекуррентные числа можно представить также в виде сумм биномиальных составляющих:
S1 = ![]() , S5 =
, S5 = 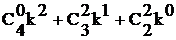 ,
,
S2 = ![]() , S6 =
, S6 = 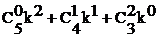 ,
,
S3 = 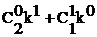 , S7 =
, S7 = 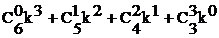 ,
,
S4 = 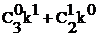 , S8 =
, S8 = 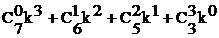 .
.
Мультирекуррентные последовательности последовательности чисел являются фундаментальными алгебраическими моделями многих физических процессов и явлений в природе, науке и техники (тепло - и массоперенос и др.), в том числе в теории электрических цепей, железнодорожных рельсовых цепей, электрических фильтрах и др. В целом можно отметить, что мультирекуррентные последовательности таят еще много не раскрытых особенностей и ждут своих исследователей.
Нечетных и четных членов лестничной последовательности чисел (1) связаны с гиперболическими функциями и определяются по формулам, установленным [6]:
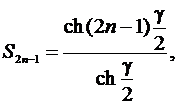
 (2) где γ = ln p1, p1 – корень характеристического уравнения p2 – (2 + k) p + 1 = 0.
(2) где γ = ln p1, p1 – корень характеристического уравнения p2 – (2 + k) p + 1 = 0.
Корни квадратного уравнения:
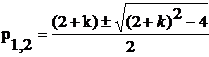
Из формул (2) могут быть получены формулы соответствующие частным случаям (при любом k) рекуррентных последовательностей. Так, в случае k = 1 последовательность (1) превращается в классическую последовательность Фибоначчи. Для k = 1, р1 = 2,618 и после преобразования (2) получим
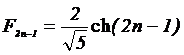
![]()

![]() , γ = 0,962.
, γ = 0,962.
Формулы для определения нечетных и четных членов Люка
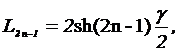
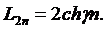 γ = 0,962.
γ = 0,962.
Рассмотрим цепочечно соединенные три четырехполюсники (n = 3) с параметрами k = R1/R2 = 1, kн = R1 /Rн и нагрузкой Rн. (рисунок 2),
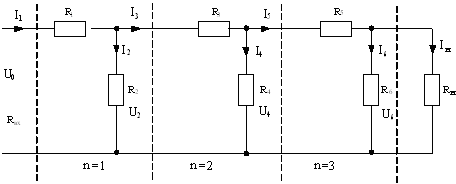
Рисунок 2 – Однородная лестничная электрическая цепь (n = 3)
Из анализа цепи можно установить следующие выражения токов цепи:
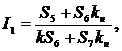
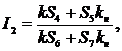
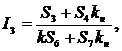
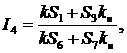
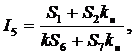
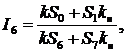
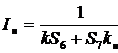 .
.
Токи цепи формируются двумя последовательностями (спиралями типа Фибоначчи). Первая – основная последовательность Фибоначчи, вторая – производная (модифицированная) последовательность типа Фибоначчи, которая определяется сопротивлением нагрузки Rн.
Входное сопротивление цепи
![]()
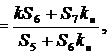
где U0 и I 1 соответственно напряжение и ток на входе цепи (см. рисунок 2).
В случае холостого хода (Rн = ∞, kн = 0) и короткого замыкания
(Rн = 0, kн = ∞) входные сопротивления соответственно равны
![]()
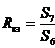 .
.
Коэффициент передачи цепи
К![]() =
= ![]() ,
,
где U0 и Uн напряжение соответственно на входе и выходе (нагрузке) цепи (см. рисунок 2).
В случае холостого хода (Rн = ∞, kн = 0) и короткого замыкания (Rн = 0, kн = ∞) коэффициент передачи соответственно равен:
Kxx =. S7, Kкз =. S6.
Аналогично могут быть получены формулы входных сопротивлений и коэффициента передачи и для других последовательностей (Rн).
Таким образом, применение мультирекуррентных (лестничных) чисел позволяет значительно упростить анализ лестничных однородных электрических цепей, а также упростить моделирование многих физических процессов в системах с сосредоточенными и распределенными однородными, параметрами в природе, науке и технике [2, 6].
Список литературы:
1. Семенюта, пропорция в природе и искусстве / ,
. – Гомель : БелГУТ, 2002. – 82 с.
2. Семенюта, линейных электрических цепей методом лестничных чисел /
. – Гомель : БелГУТ, 2010. – 109 с.
3. Семенюта, основы красоты – гармонические пропорции /
. – Гомель : БелГУТ, 2010. – 178 с.
4. Семенюта, пропорции в науке и технике / . – Гомель : БелГУТ, 20с.
5. Stakhov, A. The Mathematics of Harmony – From Euclid to comtemporary Mathematics and Computer Science / А. Stakhov. World Scientific : 2009. – 676 c.
6. Семенюта, Н. Ф. О связи рекуррентных числовых последовательностей и гиперболических функций / // Применение АВМ и ЭЦВМ к решению некоторых задач механики деформируемых тел. – Гомель : БелИИЖТ, 1972. – Вып. 114. – С. 39–43.




