ФМЭ, уч. г. Микроэкономика, модуль-3
____________________________________________________________________________________________________________
Семинар 26.
Тема: Олигополия: картель, динамическая олигополия
1. Презентация зссе
2. Решение задач.
Задача 1. Рассмотрите две фирмы, которые в каждый период 
игры, длящейся бесконечное число периодов, конкурируют по Бертрану, дисконтируя свои будущие выигрыши в соответствии с коэффициентом дисконтирования 
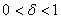. Обе фирмы имеют одинаковые постоянные предельные издержки 
. Найдите условия, при которых фирмы, используя стратегии возвращения к равновесию по Нэшу, поддерживают на рынке монопольную цену в совершенном в подыграх равновесии по Нэшу, если рыночный спрос в период имеет вид: 
, где 
.
Задача 2. Рассмотрим дуополию по Курно в отрасли, где функция спроса P(Q) = a – bQ, а предельные издержки обеих фирм постоянны, причем 0 < c1 < c2 < a. Предположим, фирмы объединились в картель. Найдите выпуск каждой участницы картеля.
Задача 3. Рассмотрите две фирмы, имеющие одинаковые функции издержек 
, 
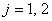, одновременно и независимо устанавливающие цены. Функции спроса на продукцию первой и второй фирмы имеют вид: 
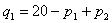и 
, соответственно.
(а) Найдите равновесные цены, выпуски фирм и прибыли. Приведите графическую иллюстрацию (в пространстве цен).
(б) Предположим теперь, что сначала первая фирма устанавливает цену, а затем вторая фирма, наблюдая цену, установленную первой фирмой, принимает решение о том, какую цену установить. Найдите равновесные цены, выпуски фирм и прибыли.
(в) Покажите, что в пространстве цен равновесие характеризуется касанием изопрофиты первой фирмы и функции реакции второй фирмы. Приведите графическую иллюстрацию.
Задача 4. Пусть некий товар продается на двух идентичных независимых рынках (
и 
). На каждом рынке действуют две фирмы, конкурирующие путем одновременного выбора цен. Игра длится бесконечное число периодов. Обе фирмы имеют одинаковые постоянные предельные издержки и используют стратегии возвращения к равновесию по Нэшу. На рынке эти фирмы встречаются каждый период, а на рынке эти же фирмы осуществляют продажи лишь по четным периодам. Пусть дисконтный фактор равен 
для любых двух соседних периодов, причем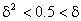 
.
(а) Покажите, что в заданном диапазоне для монопольная цена не может быть поддержана в качестве совершенного в подыграх равновесия по Нэшу, если фирмы встречаются только на рынке .
(б) Покажите, что при взаимодействии на обоих рынках монопольная цена может быть достигнута в качестве совершенного в подыграх равновесия при некоторых 
из рассматриваемого интервала. Укажите все такие значения .