математичне моделювання та обчислювальні методи
УДК 681.324
Владимир Михайлович Дубовой, Елена Дмитриевна Никитенко
Винницкий национальный технический университет, Винница
ОЦЕНКА ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНОГО ПРОЦЕССА СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Анотація. У статті вирішується задача оцінки швидкості виконання перетворень при моделюванні статистичних характеристик систем на основі GPGPU комплексів послідовно-паралельної обробки інформації. Розглянуто узагальнена задача координації послідовно-паралельного процесу статистичного моделювання для послідовних кроків перетворення вихідної інформації. Процеси координації проаналізовані з застосуванням діаграм Ганта. Правила виконання операцій моделювання ґрунтуються на операторному методі перетворень законів розподілу ймовірностей, який використовує інтегральні оператори. У роботі синтезована узагальнена модель координації паралельних процесів і перевірено її адекватність на прикладі її застосування до процесу обробки зображень. Розроблений підхід дозволяє сформувати критерій для вибору оптимального розміру блоків даних при паралельній обробці і скоротити час моделювання.
Ключові слова: статистичне моделювання, модель координації, послідовно-паралельна обробка, діаграма Ганта.
Аннотация. В статье решается задача оценки скорости выполнения преобразований при моделировании статистических характеристик систем на основе GPGPU комплексов последовательно-параллельной обработки информации.
Рассмотрена обобщенная задача координации последовательно-параллельного процесса статистического моделирования для последовательных шагов преобразования исходной информации. Процессы координации проанализированы с применением диаграмм Ганта. Правила выполнения операций моделирования основываются на операторном методе преобразований законов распределения вероятностей, который использует интегральные операторы. В работе синтезирована обобщенная модель координации параллельных процессов и проверена ее адекватность на примере ее применение к процессу обработки изображений. Разработанный подход позволяет сформировать критерий для выбора оптимального размера блоков данных при параллельной обработке и сократить время моделирования.
Ключевые слова: статистическое моделирование, модель координации, последовательно-параллельная обработка, диаграмма Ганта.
Abstract. The article is devoted to evaluation of speed of transformation to be performed while modeling the statistical characteristics of system based on GPGPU complex of sequential - parallel data processing. A generalized task of coordinating a sequential-parallel process of statistical modeling for sequential steps of transformation of the initial information. The processes of coordination analyzed using Gantt charts. Terms of performance of modeling operations based on the operator conversion method of distribution laws of probabilities, that uses integral operators. In tbe article were synthesized and tested for adequacy generalized model of coordination of parallel processes and considered its application to image processing. The developed approach allows you to create criteria for the selection of the optimum size of the data blocks in parallel processing and to reduce the simulation time.
Keywords: statistical modeling, coordination model, sequential - parallel processing, the Gantt chart.
Введение
Статистическое моделирование является одним из основных способов системного анализа и проектирования разнообразных систем массового обслуживания, информационно-измерительных систем и т. п. [1]. Такое моделирование связано с необходимостью выполнения большого объема преобразований, зависящего от размерности моделируемой системы и требуемой точности моделирования. Повышение скорости выполнения таких преобразований в системах реального времени является важной научно-прикладной проблемой.
Актуальность
Для статистического моделирования используются программно-аппаратные системы. Наибольшее распространение получили комплексы на основе GPSS [2], система моделирования на основе специализированных аппаратных вычислителей [3], параллельные системы моделирования на платформе GP GPU [4]. Управление их работой приводит к необходимости решения задачи координации [5]. В литературе [6-8] рассматриваются методы координации применительно к управлению технологическими процессами. Однако не рассмотрена задача распределения ресурсов во взаимосвязи с задачей синхронизации параллельных процессов. Аналогом ресурсов при обработке изображений является массив данных изображения. Отсутствие общего решения задачи координации процессов статистического моделирования не позволяет сформировать критерий для оптимального управления процессом моделирования, что обуславливает актуальность задачи оценки характеристик последовательно-параллельного процесса статистического моделирования с учетом процессов координации обработки данных.
Постановка задачи
Рассмотрим обобщенную задачу координации последовательно-параллельного процесса статистического моделирования для 
последовательных шагов преобразования исходной информации (рис. 1).
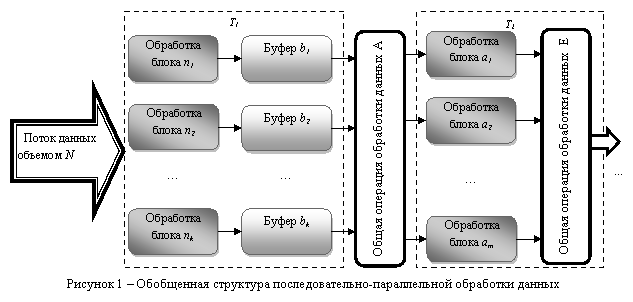Определены правила выполнение операций моделирования. За основу определения этих операций принят операторный метод преобразования законов распределения вероятностей [3], использующий интегральные операторы вида
,
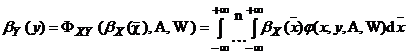где 
- функция статистического распределения, 
- ядро преобразования, 
– статистические моменты функции распределения, 
– параметры преобразования.
Так преобразования для унарных нелинейных операций вида 
.
, (1)
Для бинарных операций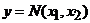 
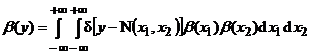. (2)
Для интегро-дифференциальных преобразований, характеризуемых импульсной передаточной функцией 
:
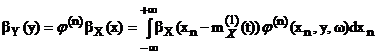, (3)
где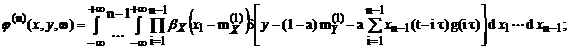 
; 
; 
; 
;
.
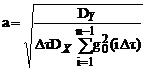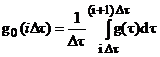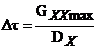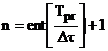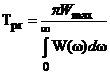Значения функции распределения вероятностей поступают на вход схемы рис.1 параллельным потоком. Поток объемом 
разделяется на кластеры количеством 
. Каждый кластер информации 
, поступает на блок обработки информации, производительностью 
. Каждому блоку соответствует буфер 
, максимальной вместимостью 
. Информация после обработки поступает к общему блоку обработки данных в определенной последовательности и обрабатывается с производительностью
. Обработанная информация поступает на параллельные блоки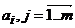 
, и снова на блок обработки всей информации 
.
Целью статьи является разработка подхода к оценке характеристик последовательно-параллельного процесса статистического моделирования с учетом процессов координации обработки данных. Для этого необходимо оценить временные характеристики системы моделирования при оптимальной синхронизации параллельных процессов.
Методы решения задачи
Для решения задачи представим операторные преобразования (1) – (3) в виде специализированных блоков, реализуемых на базе GP GPU.
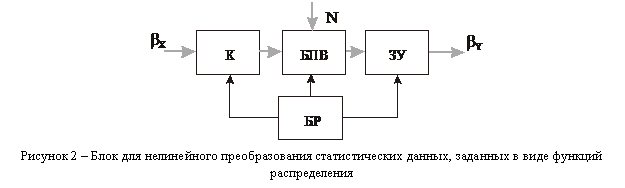
Блок для нелинейного преобразования статистических данных, заданных в виде функций распределения, (рис. 2) состоит из коммутатора (К), блока развертки (БР), блока параллельного вычисления (БПВ) и запоминающего устройства (ЗУ). Функция распределения задается в виде 
дискретных значений 
и подается одновременно со значениями, которые вырабатывает блок развертки, на соответствующие входы коммутатора. Из коммутатора значения поступают в блок параллельного вычисления, где выполняется дифференцирование и умножение, полученный результат заносится в запоминающее устройство. При прохождении полного цикла моделирования на выходе запоминающего устройства воспроизводятся значения функции распределения после нелинейного преобразования в соответствии с формулой (1).
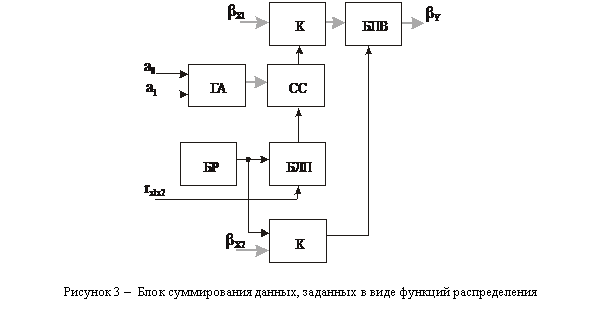
Структура блока суммирования статистических данных, заданных в виде функций распределения, представлена на рис.3, где обозначено: ГА – генератор аргумента, СС – схема совпадения, БЛП – блок линейного преобразования.
Блок работает следующим образом. Функции распределения задаются в виде дискретных значений 
, 
и подаются на соответствующие коммутаторы. На вход блока линейного преобразования поступает значение 
, вырабатываемое блоком развертки и формируется значение функции
,
поступающее на управляющий вход схемы совпадения, где оно сравнивается с текущими значениями 
, которые формирует генератор аргумента. Таким образом, на коммутатор поступают значения, которые выбирают данные, индексы которых удовлетворяют соотношению
 |
.
Тогда на выходе коммутатора 
формируются значения функции 
, которые поступают на вход блока параллельного вычисления БПВ, на второй вход поступают значения функции 
. В блоке параллельного вычисления выполняются операции умножения и интегрирования. При прохождении полного цикла преобразования на выходе БПВ формируются значения функции распределения сумы статистических данных 
в соответствии с формулой (2).
 |
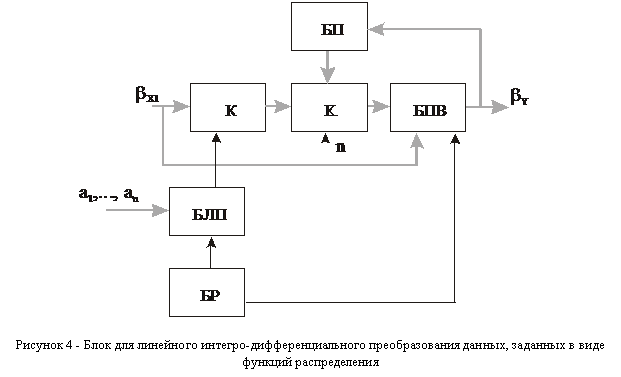Блок для линейного интегро-дифференциального преобразования статистических данных, заданных в виде функций распределения, имеет структуру, представленную на рис.4
Функция распределения задается в виде дискретных значений 
и подается одновременно на входы коммутатора и блока параллельного вычисления. В блоке развертки формируются текущие значения 
и подаются на входы блока параллельного вычисления и блока линейного преобразования. В блок линейного преобразования также подаются значения постоянных коэффициентов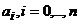 
, значения которых вычисляются в соответствии с формулой для ядра преобразования (3). На выходе блока линейного преобразования формируются значения
.
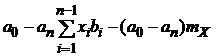На управляющий вход второго коммутатора подается значение , которое равно количеству циклов интегрирования. С выходов блока параллельного вычисления, где производится умножение и интегрирование, значения подаются в блок памяти. При прохождении 
циклов интегрирования на выходе блока параллельного вычисления формируются функции распределения 
после линейного интегро-дифференциального преобразования в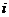 
-й времени. При прохождении полного цикла моделирования на выходе блока интегрирования формируются значения обобщающей функции после линейного интегро-дифференциального преобразования для дискретных значений 
.
Таким образом, последовательное выполнение операций статистического моделирования сочетается с параллельным преобразованием данных на каждой операции. Между операциями происходит перекоммутация данных от каналов вывода предыдущей операции на каналы вывода последующей операции, которая выполняется последовательно. Такой конвейерный метод требует координации процессов поступления данных от одной операции к другой. Целью координации процессов является уменьшение общего времени моделирования 
.
Модель координации процессов обработки данных покажем в виде диаграммы Ганта (рис. 5) [9].
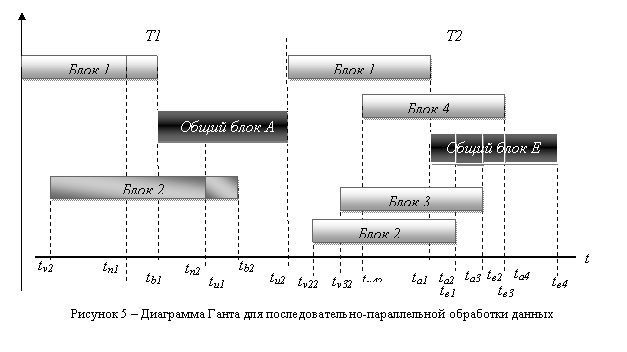
Время работы системы состоит из суммы времени выполнения всех последовательных шагов:
. (4)
Поскольку определен порядок поступления элементов на блок совместной обработки данных, то можно сказать, что первый блок обработает информацию раньше, а последний - позже. Тогда
, (5)
где 
– время простоя блока, которое зависит от порядка поступления соответствующего кластера в блок совместной обработки данных.
Очевидно
, (6)
где 
- время работы блока обработки, которое зависит от производительности этого блока и количества данных 
(7)
- время буферизации данных в блоке памяти, представляет собой разницу между временем заполнения 
и временем отдачи данных 
.
Время заполнения буфера памяти и время вывода данных из буфера памяти:
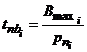, (8)
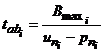, (9)
где - производительность обработки кластера данных в блоке .
Время нахождения данных в блоке памяти:
. (10)
Тогда 
:
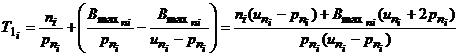(11)
Время обработки всех данных в блоке :
, (12)
где - общее количество данных, 
- коэффициент сжатия при обработке данных.
Блок 
аналогичен 
, но с другим количеством данных и другим количеством кластеров, то есть
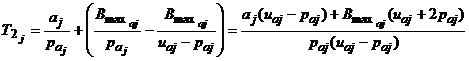, (13)
где 
- количество данных в кластере, 
- порядковый номер кластера, 
.
Время обработки всех данных в блоке :
(14)
где - общее количество информации, 
- коэффициент сжатия.
Общее время для двух аналогичных блоков будет состоять из суммы времен «медленных» блоков:
(15)
Для проверки адекватности модели (15) построим частные зависимости 
, 
, 
, 
, 
, получаемые из (15) фиксацией остальных переменных. Параметры зависимостей пронумерованы и приведены к диапазону (0, 100).
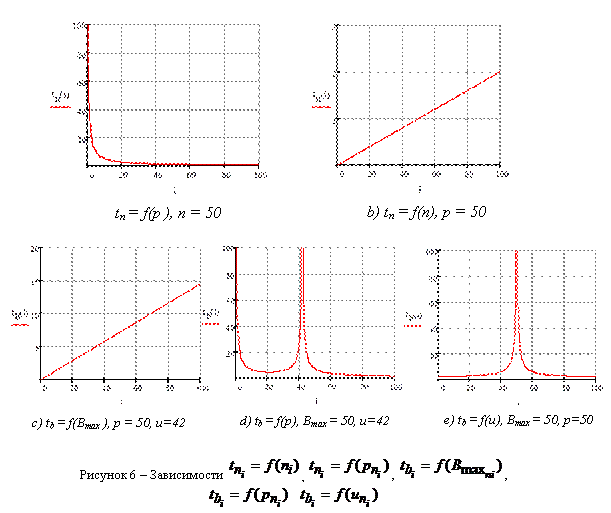
Анализ зависимостей (рис. 6) показывает соответствие расчетной и имитационной модели. Так, рис. 6, a показывает убывание времени выполнения операции с ростом производительности, а рис. 6, b и рис. 6, c показывают рост времени выполнения отдельной операции от количества данных и размера буфера. Наиболее интересна и нетривиальна зависимость на рис. 6, d, которая показывает наличие минимума времени буферизации при изменении производительности обработки и размера блоков данных. Оптимизация размера блоков позволит сократить общее время моделирования.
Выводы
Разработанный подход к оценке характеристик последовательно-параллельного процесса статистического моделирования с учетом процессов координации обработки данных позволяет сформировать критерий для выбора оптимального размера блоков данных при параллельной обработке и сократить время моделирования.
Список литературы
1. моделирование систем массового обслуживания / , – М.: Советское радио. – 1978. – 248 с.
2. Общецелевая система моделирования GPSS World / Exponenta. ru (Электронный документ) Режим доступа: http://www. exponenta. ru/soft/others/gpss/gpss. asp
3. Глонь систем керування в умовах невизначеності. Монографія./ , – Вінииця: УНІВЕРСУМ – Вінниця, 2003. – 174 c.
4. What is GPU accelerated computing / NVIDIA (Электронный документ) Режим доступа: http://www. /object/what-is-gpu-computing. html
5. Woodside C. M. Fast Allocation of Processes in Distributed and Parallel Systems / C. M. Woodside, and G. G. Monforton // IEEE Transactions on parallel and distributed systems. – 1993. – P. 164-174.
6. Katrenko A. V. Mechanisms of coordination in complex hierarchical systems. / A. V. Katrenko I. V. Savka - 2008 - URL: http://vlp. /files/16_1.pdf
7. Ladanyuk A. P. System task coordination continuous technological complexes type / A. P. Ladanyuk, D. A. Shumyhay, R. O. Boyko - URL:http://dspace. nuft. /jspui/bitstream/123456789/4444/1/Sh_3.pdf.
8. Mesarovic, M. D. Theory of Hierarchical Multilevel Systems / M. D. Mesarovic, D. Macko, Y. Takahara,. — Published by Academic Press, Inc., 1972. – 344 p.
9. Прийняття рішень в управлінні розгалуженими технологіч-ними процесами : [монографія] / , , І. В. Пилипенко, . — Вінниця : ВНТУ, 2013. — 223 c.
Данные про авторов
- д. т.н., проф., зав. кафедрой компьютерных систем управления, Факультет компьютерных систем и автоматики, Винницкий национальный технический университет,
(0432) 44-01-57 (мобильный: 8-097-214-21-60), v. *****@***com
Volodymyr Mikhailovich Dubovoy Doctor of Technical Sciences, Professor, Head of Computer control systems departmen, Faculty for Computer Systems and Automation, Vinnytsia National Technical University, (0432) 44-01-57 (мобильный: 8-097-214-21-60), v. *****@***com
Дубовой Володимир Михайлович - д. т.н., проф., зав. кафедри комп’ютерних систем управління, Факультет комп’ютерних систем і автоматики, Вінницький національний технічний університет, (0432) 44-01-57 (мобільний: 8-097-214-21-60), v. *****@***com
Lena Dmitrievna Nikitenko - Ph. D., Associate Professor of Computer control systems departmen, Faculty for Computer Systems and Automation, Vinnytsia National Technical University, университет (0432) 27-20-44 (мобільний: 8-067-299-43-13), lena260784@gmaі
- к. т.н., доцент кафедры компьютерных систем управления, Факультет компьютерных систем и автоматики, Винницкий национальный технический университет (0432) 27-20-44 (мобільний: 8-067-299-43-13), lena260784@gmaі
Никитенко Олена Дмитрівна - к. т.н., доцент кафедри комп’ютерних систем управління, Факультет комп’ютерних систем і автоматики, Вінницький національний технічний університет, (0432) 27-20-44 (мобільний: 8-067-299-43-13), lena260784@gmaі
