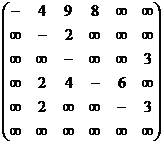Контрольная работа №1 по дисциплине «Исследование операций»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ
ВЫПОЛНИТЬ ВАРИАНТ 2
Структура контрольной работы
Контрольная работа состоит из двух частей: теоретической и практической.
Теоретическая часть выполняется в виде ответа на теоретический вопрос согласно варианту.
Практическая часть состоит из двух практических заданий.
Вариант для выполнения данной контрольной работы выбирается следующим образом: сумма двух последних цифр зачетной книжки студента делится с остатком на 10. К остатку от деления прибавляется единица. Полученное число является номером варианта.
Структура контрольной работы:
1. Титульный лист.
2. Содержание.
3. Ответ на теоретический вопрос.
4. Описание выполнения практических заданий.
5. Список литературы. (5-10 наименований)
Текст должен быть представлен в редакторе Word, cтраницы работы должны быть пронумерованы, на каждой из них справа оставлены поля размером 2,5-3 см для замечаний и предложений рецензента, шрифт - 14, одинарный межстрочный интервал. В конце реферата приводится список использованной литературы, ставится подпись и дата выполнения.
Вопросы для выполнения теоретической части задания
1. Понятия, принципы и средства исследования операций.
2. Прикладные аспекты исследования операций.
3. Вероятностные модели операций. Анализ случайных явлений.
4. Случайные процессы. Потоки событий. Основные понятия теории массового обслуживания.
5. Системы массового обслуживания с отказами.
6. Системы массового обслуживания с очередью.
7.Основные понятия теории игр. Определение игры. Разновидности игровых моделей.
8. Матричные игры с нулевой суммой. Способы поиска оптимальных решений.
9. Методы исследования кооперативных игр.
10. Неформальные методы исследования операций.
Практическое задание №1
Решение задач теории массового обслуживания
Методические указания
При исследовании операций часто приходится сталкиваться с системами, предназначенными для многоразового использования при решении однотипных задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания (СМО).
Главная особенность процессов массового обслуживания – случайность. При этом имеются две взаимодействующие стороны – обслуживаемая и обслуживающая.
Примерами процессов этого типа являются:
1) обслуживание покупателей в сфере розничной торговли;
2) транспортное обслуживание;
3) медицинское обслуживание населения;
4) ремонт аппаратуры, машин, механизмов, находящихся в эксплуатации;
5) обработка документов в системе управления;
6) туристическое обслуживание.
Неотъемлемой частью системы массового обслуживания является узел обслуживания, через который осуществляется взаимодействие входного и выходного потоков заявок. В случае транспортного обслуживания каналом может считаться отдельная единица транспортного средства.
Вид графической модели зависит как от числа каналов n, так и от допустимой длины очереди m. По указанным признакам различается ряд типов СМО, перечисленных в табл. 1.
Таблица 1
Типы систем массового обслуживания
№ п/п | Параметры СМО | Тип СМО | |
n | m | ||
1 | 1 | 0 | Одноканальная, без очереди |
2 | n > 1 | 0 | Многоканальная, без очереди |
3 | 1 | 1 < m <∞ | Одноканальная, с ограниченной очередью |
4 | n > 1 | 1 < m <∞ | Многоканальная, с ограниченной очередью |
5 | 1 | m = ∞ | Одноканальная, с неограниченной очередью |
6 | n > 1 | m = ∞ | Многоканальная, с неограниченной очередью |
По числу обслуживающих каналов различают одноканальные и многоканальные СМО.
Находящиеся в СМО заявки могут либо ожидать обслуживания, либо находиться под обслуживанием. Часть заявок, ожидающих обслуживания, образует очередь.
В зависимости от целочисленного значения m используются следующие названия в классификации типов СМО:
1) m = 0 – без очереди;
2) m > 0 – с очередью.
Если число мест в очереди m является конечным, то в СМО могут происходить отказы в предоставлении обслуживания некоторым заявкам. В связи с этим СМО указанного типа называются системами с отказами. Отклоняются от обслуживания те заявки, в момент прихода которых все места в очереди случайно оказались занятыми, или, если m = 0, все каналы оказались занятыми. Считается, что заявка, получившая отказ в обслуживании, навсегда теряется для СМО. Таким образом, пропускная способность СМО этого типа всегда меньше 100 %.
Если m не ограничено, что иногда условно записывают как m = ![]() , то соответствующая СМО называется системой с ожиданием. В СМО данного типа пришедшая заявка при отсутствии возможности немедленного обслуживания ожидает обслуживания, какой бы длинной ни были очередь и продолжительность времени ожидания.
, то соответствующая СМО называется системой с ожиданием. В СМО данного типа пришедшая заявка при отсутствии возможности немедленного обслуживания ожидает обслуживания, какой бы длинной ни были очередь и продолжительность времени ожидания.
Некоторые обозначения, применяемые в теории массового обслуживания, для формул:
n – число каналов в СМО;
λ – интенсивность входящего потока заявок Пвх;
v – интенсивность выходящего потока заявок Пвых;
μ – интенсивность потока обслуживания Поб;
ρ – показатель нагрузки системы (трафик);
m – максимальное число мест в очереди, ограничивающее длину очереди заявок;
i – число источников заявок;
pк – вероятность k-го состояния системы;
pо – вероятность простаивания всей системы, т. е. вероятность того, что все каналы свободны;
pсист – вероятность принятия заявки в систему;
pотк – вероятность отказа заявке в принятии ее в систему;
роб – вероятность того, что заявка будет обслужена;
А – абсолютная пропускная способность системы;
Q – относительная пропускная способность системы;
![]() оч – среднее число заявок в очереди;
оч – среднее число заявок в очереди;
![]() об – среднее число заявок под обслуживанием;
об – среднее число заявок под обслуживанием;
![]() сист – среднее число заявок в системе;
сист – среднее число заявок в системе;
![]() оч – среднее время ожидания заявки в очереди;
оч – среднее время ожидания заявки в очереди;
![]() об – среднее время обслуживания заявки, относящееся только к обслуженным заявкам;
об – среднее время обслуживания заявки, относящееся только к обслуженным заявкам;
![]() сис – среднее время пребывания заявки в системе;
сис – среднее время пребывания заявки в системе;
![]() ож – среднее время, ограничивающее ожидание заявки в очереди;
ож – среднее время, ограничивающее ожидание заявки в очереди;
![]() – среднее число занятых каналов.
– среднее число занятых каналов.
Абсолютная пропускная способность СМО А – среднее число заявок, которое может обслужить система за единицу времени.
Относительная пропускная способность СМО Q – отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок.
Примеры решения задач систем массового обслуживания
При решении задач массового обслуживания необходимо придерживаться нижеприведенной последовательности:
1) определение типа СМО по табл. 1;
2) выбор формул в соответствии с типом СМО;
3) решение задачи;
4) формулирование выводов по задаче.
Задача 1. На сортировочную станцию прибывают составы с интенсивностью 0,9 состава в час. Среднее время обслуживания одного состава 0,7 часа. Определить показатели эффективности работы сортировочной станции: интенсивность потока обслуживаний, среднее число заявок в очереди, интенсивность нагрузки канала (трафик), вероятность, что канал свободен, вероятность, что канал занят, среднее число заявок в системе, среднее время пребывания заявки в очереди, среднее время пребывания заявки в системе.
Решение. Сортировочную станцию можно рассматривать как одноканальную СМО с неограниченным ожиданием (т. е. с очередью). Таким образом, параметры системы: число каналов n = 1, число мест в очереди m = ![]() .
.
Интенсивность входящего потока λ = 0,9 состава в час, среднее время обслуживания одной заявки ![]() об = 0,7 ч, интенсивность потока обслуживаний
об = 0,7 ч, интенсивность потока обслуживаний
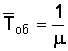 , (1)
, (1)
μ = 1/0,7 = 1,429. Таким образом, нагрузка системы
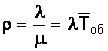 , (2)
, (2)
ρ = 0,9/1,429 = 0,63, или ρ = 0,9 ∙ 0,7 = 0,63.
Среднее число составов, ожидающих обслуживания,
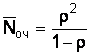 , (3)
, (3)
![]() оч = 0,632/(1 – 0,63) = 1,073.
оч = 0,632/(1 – 0,63) = 1,073.
Так как ρ < 1, то очередь составов на сортировку не может бесконечно возрастать, значит, предельные вероятности существуют. Вероятность того, что станция свободна p0, рассчитывается по следующей формуле:
pk = ρk(1 – ρ); k = 0,1,2…
p0 =1 – ρ. (4)
p0 = 1 – 0,63 = 0,37, тогда вероятность того, что станция занята pзан = 1 – – 0,37 = 0,63.
Среднее число заявок (составов) в системе (на сортировочной станции) рассчитывается по следующей формуле:
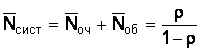 , (5)
, (5)
где ![]() ;
; ![]() сист = 0,63/1 – 0,63 = 1,703 или
сист = 0,63/1 – 0,63 = 1,703 или ![]() сист = 0,63 + 1,073 = 1,703.
сист = 0,63 + 1,073 = 1,703.
Среднее время пребывания заявки (состава) в очереди (в ожидании сортировки)
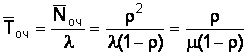 , (6)
, (6)
![]() оч = 1,073/0,63 = 0,632/(0,9(1 – 0,63)) = 0,63/(1,429(1 – 0,63)) = 1,19.
оч = 1,073/0,63 = 0,632/(0,9(1 – 0,63)) = 0,63/(1,429(1 – 0,63)) = 1,19.
Среднее время пребывания заявки (состава) в системе (на сортировочной горке под обслуживанием в ожидании обслуживания)
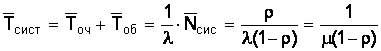 , (7)
, (7)
![]() сист = 0,7 + 1,19 = 0,63/(0,9(1 – 0,63)) = 1,703/0,9 = 1/(1,429(1 – 0,63)) = 1,89.
сист = 0,7 + 1,19 = 0,63/(0,9(1 – 0,63)) = 1,703/0,9 = 1/(1,429(1 – 0,63)) = 1,89.
Вывод. Очевидно, что скорость обслуживания составов на сортировочной станции невысокая, так как время на ожидание обслуживания (1,19 ч) превышает время на обслуживание (0,7 ч). Для повышения эффективности работы сортировочной горки необходимо уменьшить время обслуживания одного состава или увеличить число сортировочных станций.
Задача 2. Интенсивность потока пассажиров в кассах железнодорожного вокзала составляет λ = 1,35 чел. в мин. Средняя продолжительность обслуживания кассиром одного пассажира ![]() об = 2 мин. Определить минимальное количество кассиров n = nmin, при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при n = nmin(вероятность того, что в узле расчета отсутствуют покупатели, вероятность очереди, среднее число заявок находящихся в очереди, среднее время пребывания заявки в очереди, среднее число заявок, находящихся в системе, среднее время пребывания заявки в системе, доля занятых обслуживанием кассиров, абсолютная пропускную способность) (табл. 4.3).
об = 2 мин. Определить минимальное количество кассиров n = nmin, при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при n = nmin(вероятность того, что в узле расчета отсутствуют покупатели, вероятность очереди, среднее число заявок находящихся в очереди, среднее время пребывания заявки в очереди, среднее число заявок, находящихся в системе, среднее время пребывания заявки в системе, доля занятых обслуживанием кассиров, абсолютная пропускную способность) (табл. 4.3).
Указание. Прежде чем использовать формулы предельных вероятностей, необходимо быть уверенным в их существовании, ведь в случае, когда время t → ![]() , очередь может неограниченно возрастать. Доказано, что если ρ < 1, т. е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если ρ ≥ 1, очередь растет до бесконечности. Очередь не будет возрастать до бесконечности при условии ρ /n < 1, т. е. при n > ρ.
, очередь может неограниченно возрастать. Доказано, что если ρ < 1, т. е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если ρ ≥ 1, очередь растет до бесконечности. Очередь не будет возрастать до бесконечности при условии ρ /n < 1, т. е. при n > ρ.
Решение. n > 1, m = ![]() , т. е. имеем многоканальную систему с неограниченной очередью. По условию λ = 1,35 (1/мин). Показатель нагрузки системы определяется по формуле (2): ρ = 1,35∙2 = 2,7.
, т. е. имеем многоканальную систему с неограниченной очередью. По условию λ = 1,35 (1/мин). Показатель нагрузки системы определяется по формуле (2): ρ = 1,35∙2 = 2,7.
Очередь не будет возрастать до бесконечности при условии ρ / n < 1, т. е. при n > ρ = 2,7. Таким образом, минимальное количество контролеров-кассиров nmin = 3.
Найдем характеристики обслуживания СМО при nmin = 3.
Вероятность того, что в узле расчета отсутствуют покупатели, определяется по формуле
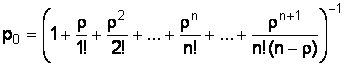 , (8)
, (8)
р0 = (1 + 2,7 + 2,72/2! + 2,73/3! + 2,74/3! ∙ (3 – 2,7))–1 = 0,025, т. е. в среднем 2,5 % времени контролеры-кассиры будут простаивать.
Вероятность того, что в узле расчета будет очередь, определяется по формуле
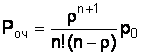 , (9)
, (9)
Роч = (2,74/3!(3 – 2,7)) ∙ 0,025 = 0,735.
Среднее число покупателей, находящихся в очереди, определяется по формуле
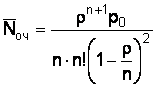 , (10)
, (10)
![]() оч = (2,74/3 ∙ 3!(1 – 2,7/3)2) ∙ 0,025 = 7,35.
оч = (2,74/3 ∙ 3!(1 – 2,7/3)2) ∙ 0,025 = 7,35.
Среднее время ожидания в очереди определяется по формуле
![]() , (11)
, (11)
![]() оч = 7,35/1,35 = 5,44 мин.
оч = 7,35/1,35 = 5,44 мин.
Среднее число покупателей в узле расчета определяется по формуле
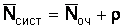 , (12)
, (12)
![]() сист = 7,35 + 2,7 = 10,05.
сист = 7,35 + 2,7 = 10,05.
Среднее время нахождения покупателей в узле расчета определяется по формуле
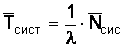 , (13)
, (13)
![]() сис = 10,05/1,35 = 7,44 мин.
сис = 10,05/1,35 = 7,44 мин.
Среднее число контролеров-кассиров, занятых обслуживанием покупателей, определяется по формуле
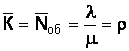 , (14)
, (14)
![]() = 2,7.
= 2,7.
Коэффициент (доля) занятых обслуживанием контролеров-кассиров
![]() = ρ/n = 2,7/3 = 0,9.
= ρ/n = 2,7/3 = 0,9.
Абсолютная пропускная способность узла расчета А = 1,35 (1/мин), или 81 (1/ч), т. е. 81 покупатель в час.
Вывод. Анализ характеристик обслуживания свидетельствует о значительной перегрузке узла расчета при наличии трех кассиров.
Задача 3. На грузовой станции имеется два выгрузочных фронта. Интенсивность подхода составов под выгрузку составляет 0,4 состава в сутки. Среднее время разгрузки одного состава – 2 суток. Приходящий поезд отправляется на другую станцию, если в очереди на разгрузку стоят более трёх составов. Оценить эффективность работы выгрузочных фронтов грузовой станции: вероятность, что выгрузочные фронты свободны, вероятность, что состав останется без разгрузки, относительную пропускную способность, абсолютную пропускную способность, среднее число поездов, ожидающих разгрузки, среднее число заявок в системе, среднее время пребывания заявки в очереди, среднее время пребывания заявки в системе.
Решение. По условию задачи n = 2, m = 3, т. е. грузовая станция представляет собой многоканальную систему с ограниченной очередью. Интенсивность потока обслуживаний определяется по формуле (1):
μ =1/2 = 0,5.
Интенсивность нагрузки канала (трафик) определяется по формуле (2): ρ = 0,4 ∙ 2 = 0,8.
Вероятность того, что выгрузочный фронт свободен, определяется по формуле
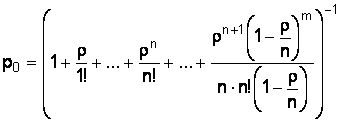 , (15)
, (15)
р0 = 0,431.
Вероятность того, что состав будет отправлен на другую станцию, определяется по формуле
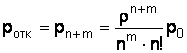 , (16)
, (16)
ротк = 0,009.
Относительная пропускная способность определяется по формуле
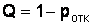 , (17)
, (17)
Q = 1 – 0,009 = 0,991.
Абсолютная пропускная способность определяется по формуле
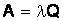 , (18)
, (18)
А = 0,4 ∙ 0,991 = 0,396, т. е. в среднем в сутки разгружается 0,4 состава.
Среднее число составов, ожидающих разгрузки, определяется по формуле
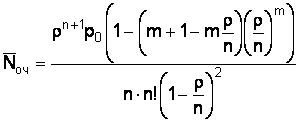 , (19)
, (19)
где ![]() = 0,21.
= 0,21.
Среднее время ожидания разгрузки определяется по формуле (11): ![]() оч = 0,21/0,4 = 0,524.
оч = 0,21/0,4 = 0,524.
Среднее число занятых фронтов (среднее число заявок под обслуживанием) определяется по формуле
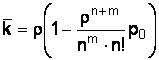 , (20)
, (20)
![]() = 0,77.
= 0,77.
Среднее число составов, находящихся у разгрузочного фронта определяется по формуле
![]() , (21)
, (21)
![]() сист = 0,21 + 0,77 = 0,98.
сист = 0,21 + 0,77 = 0,98.
Среднее время пребывания состава у разгрузочного фронта определяется по формуле (14): ![]() сис = 1,564/0,4 = 3,908.
сис = 1,564/0,4 = 3,908.
Вывод. Среднее время пребывания состава в ожидании разгрузки на другой станции невелико. Это говорит о нормальной работе выгрузочного узла.
Контрольное задание
Решить задачи 1–3 с исходными данными, которые приведены в табл. 2–4 согласно варианту.
Таблица 2
Исходные данные для решения задачи 1
Показатель | Вариант | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
λ | 0,5 | 0,8 | 0,4 | 0,6 | 0,7 | 0,5 | 0,7 | 0,6 | 0,8 | 0,4 |
| 0,3 | 0,5 | 0,6 | 0,9 | 0,2 | 0,2 | 0,4 | 0,8 | 0,3 | 0,5 |
Таблица.3
Исходные данные для решения задачи 2
Показатель | Вариант | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
λ | 1,37 | 1,62 | 1,42 | 1,83 | 1,75 | 1,55 | 1,4 | 1,65 | 1,7 | 1,3 |
| 2,3 | 2 | 1 | 2,5 | 1,5 | 1,7 | 1,2 | 2,6 | 1 | 2,5 |
Таблица.4
Исходные данные для решения задачи 3
Показатель | Варианты | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
λ | 0,5 | 0,9 | 0,5 | 0,3 | 0,6 | 0,8 | 0,9 | 0,4 | 0,6 | 0,5 |
| 2 | 1 | 1,5 | 1,4 | 1,3 | 1,2 | 1,5 | 2 | 1,9 | 1,4 |
Практическое задание №2. Нахождение кратчайшего пути в ориентированной сети с помощью алгоритма Дейкстры.
Методические указания
Задачи нахождения оптимальных маршрутов или сетевые задачи являются задачами исследования операций. Такие задачи возникают при исследовании различных процессов на транспорте и в системах связи.
Типичной задачей является задача нахождения кратчайшего пути в ориентированной сети. Одним из алгоритмов ее решения является алгоритм Дейкстры, который позволяет находить кратчайшие пути между двумя заданными вершинами в ориентированной сети. Веса дуг должны быть неотрицательными. Пусть задан взвешенный орграф![]() . Обозначим s - начало пути, t – конец пути. Алгоритм Дейкстры – это алгоритм расстановки меток. Метки присваиваются вершинам (узлам) графа, метки разделяют на временные и постоянные. Если вершине
. Обозначим s - начало пути, t – конец пути. Алгоритм Дейкстры – это алгоритм расстановки меток. Метки присваиваются вершинам (узлам) графа, метки разделяют на временные и постоянные. Если вершине ![]() присвоена временная метка
присвоена временная метка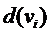 , то это означает. что существует путь длиной
, то это означает. что существует путь длиной 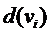 от вершины s до
от вершины s до![]() , если метка становится постоянной
, если метка становится постоянной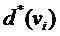 , то это означает, что найден кратчайший путь от вершины s до
, то это означает, что найден кратчайший путь от вершины s до![]() длиной
длиной 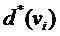 . Алгоритм состоит из двух этапов: на первом находится длина искомого кратчайшего пути, на втором – сам путь.
. Алгоритм состоит из двух этапов: на первом находится длина искомого кратчайшего пути, на втором – сам путь.
Этап I
1. Всем вершинам присваиваются начальные метки и выбирается текущая вершина ![]()
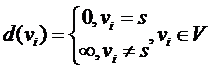 ,
, 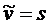
2. Изменение временных меток
Находим множество вершин![]() , непосредственно следующих за текущей вершиной
, непосредственно следующих за текущей вершиной![]() . Для всех вершин с временными метками из этого множества меняем метки во формуле
. Для всех вершин с временными метками из этого множества меняем метки во формуле
![]()
3. Замена временной метки на постоянную
Среди всех вершин с временными метками выбираем вершину с наименьшим значением метки и превращаем эту метку в постоянную
![]() ,
, 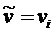
4. Проверка на конец этапа I.
Если 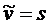 , то длина кратчайшего пути от вершины s до вершины t равна
, то длина кратчайшего пути от вершины s до вершины t равна
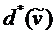 . В противном случае возвращение к пункту 2.
. В противном случае возвращение к пункту 2.
Этап I I
5. Находим множество вершин![]() , непосредственно предшествующей вершине
, непосредственно предшествующей вершине![]() . Среди всех вершин множества
. Среди всех вершин множества ![]() с постоянными метками находим вершину
с постоянными метками находим вершину ![]() , удовлетворяющую соотношению
, удовлетворяющую соотношению
![]()
Включаем дугу ![]() в путь и полагаем
в путь и полагаем 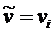 .
.
6. Проверка на конец этапа I I.
Если ![]() , то кратчайший путь от вершины s до вершины t найден. В противном случае возвращение к пункту 5.
, то кратчайший путь от вершины s до вершины t найден. В противном случае возвращение к пункту 5.
Пример По заданной матрице весов ![]() графа
графа![]() найти величину минимального пути сам путь от вершины
найти величину минимального пути сам путь от вершины ![]() до вершины
до вершины ![]() по алгоритму Дейкстры.
по алгоритму Дейкстры.
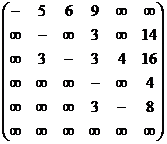
Этап I
1. ![]() ,
, 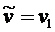
21. 
![]()
![]()
![]()
31. ![]() ,
, 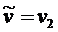
41 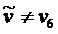 , поэтому возвращаемся к пункту 2.
, поэтому возвращаемся к пункту 2.
22. 
![]()
![]()
32. ![]() ,
, 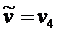
42 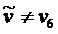 , поэтому возвращаемся к пункту 2.
, поэтому возвращаемся к пункту 2.
23. 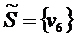
![]()
33. ![]() ,
, 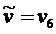
43 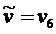 , длина кратчайшего пути от вершины
, длина кратчайшего пути от вершины ![]() до вершины
до вершины ![]() равна
равна
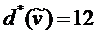
Этап I I
51. ![]()
Проверяем условие![]() всех вершин множества
всех вершин множества ![]() с постоянными метками
с постоянными метками
![]()
![]()
Включаем дугу ![]() в путь и полагаем
в путь и полагаем 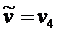 .
.
61. 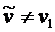 , поэтому возвращаемся к пункту 5.
, поэтому возвращаемся к пункту 5.
52. 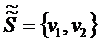
Проверяем условие![]() всех вершин множества
всех вершин множества ![]() с постоянными метками
с постоянными метками
![]()
![]()
Включаем дугу ![]() в путь и полагаем
в путь и полагаем 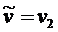 .
.
62. 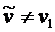 , поэтому возвращаемся к пункту 5.
, поэтому возвращаемся к пункту 5.
52. 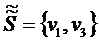
Проверяем условие![]() всех вершин множества
всех вершин множества ![]() с постоянными метками
с постоянными метками
![]()
Включаем дугу ![]() в путь и полагаем
в путь и полагаем 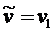 .
.
62. 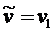 , кратчайший путь от вершины
, кратчайший путь от вершины ![]() до вершины
до вершины ![]() найден.
найден.
Кратчайший путь: ![]()

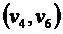 . Длина
. Длина ![]() .
.
Контрольное задание
По заданной матрице весов ![]() графа
графа![]() найти величину минимального пути сам путь от вершины
найти величину минимального пути сам путь от вершины ![]() до вершины
до вершины ![]() по алгоритму Дейкстры и сам кратчайший путь между этими вершинами.
по алгоритму Дейкстры и сам кратчайший путь между этими вершинами.
2.1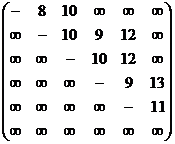 2.2
2.2 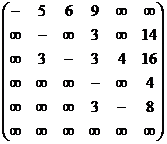
2.3 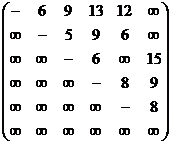 2.4
2.4 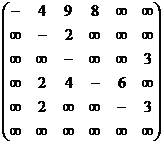
2.5  2.6
2.6 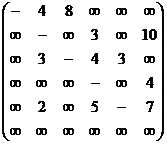
13.7 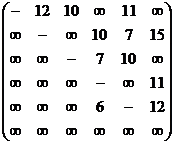 13.8
13.8 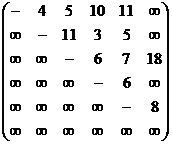
2.9 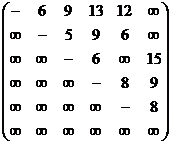 2.10
2.10