Элементы теории вероятностей. 6 класс

Элементы теории вероятностей. 6 класс

Из программы:

Случайные события, достоверные и невозможные события. Вероятность события. Классическое определение вероятности. Частота. Статистическое определение вероятности.

Учащиеся должны: знать различные способы определения вероятностей случайных событий и уметь применять их в простейших случаях.

Случайные события

Рассмотрим задачу:

В 10 часов утра из пункта А в пункт В, выехал легковой автомобиль. Успеет ли он приехать в пункт В к 3 часам дня, если расстояние между А и В 350 км, а правилами дорожного движения допускается скорость автотранспорта на этом участке до 90 км/ч?

Кажется, что ответ однозначный – успеет, т. к. за отведенные 5 часов двигаясь со скоростью 90 км/ч автомобиль может проехать 450 км, что значительно превышает расстояние между А и В. Это рассуждение основано на предположении, что на протяжении всего пути удастся выдерживать подходящую скорость, т. е. ситуация рассматривается как полностью определенная. Однако в данном рассуждении не учитывается ряд факторов, которые могут повлиять на рассматриваемую ситуацию, например, светофоры на дороге, перед которыми придется останавливаться, возможные «пробки», технические неполадки с автомобилем и т. п. Все перечисленные факторы носят случайный характер и превращают данную ситуацию в неопределенную, а ответ на вопрос задачи в неоднозначный.

Если задуматься, можно прийти к заключению, что в окружающем нас мире преобладают именно явления, в которых в той или иной степени присутствует случайность.

Но если мир устроен случайным образом, означает ли это, что в нем царит хаос, не поддающийся никакому описанию? Или существуют какие-то правила, законы, с помощью которых можно описывать случайные явления? Ответ на этот вопрос дает теория вероятностей – раздел математики, с которым вы начинаете знакомиться.

Одним из важнейших объектов, составляющих предмет теории вероятностей, является так называемое случайное событие. Под случайными событиями понимаются такие события, которые в рассматриваемых условиях могут произойти, а могут и не произойти. События принято обозначать заглавными латинскими буквами. В рассмотренном выше примере с автомобилем случайным событием является приезд автомобиля в пункт В до 3 часов дня. Это может произойти, а может и не произойти.

1. Приведите собственные примеры случайных событий. Объясните, почему вы считаете эти события случайными.

2. Сравните события А, В, С, D по возможности их появления:

А: На будущий год 15 января в Москве будет идти снег.

В: На будущий год 15 марта в Москве будет идти снег.

С: На будущий год 15 мая в Москве будет идти снег.

D: На будущий год 15 июля в Москве будет идти снег.

Различные случайные события могут иметь различную возможность произойти. Величина, характеризующая такую возможность, называется вероятностью. Для одних событий эта возможность высока, для других она меньше, иными словами, есть более вероятные и менее вероятные события.

3. В книге 500 страниц. Книгу открывают наугад. Сравните вероятности следующих событий:

А: Номер открытой страницы меньше 100.

В: Номер открытой страницы меньше 700.

С: Номер открытой страницы больше 100.

D: Номер открытой страницы больше 700.

Обоснуйте свой ответ.

Среди различных событий выделяются два предельных случая: невозможное событие – такое, которое в данных условиях не может произойти, и достоверное событие – такое, которое, наоборот, в данных условиях обязательно происходит. Эти события можно противопоставлять случайным событиям, но более продуктивно рассматривать их как особые виды случайных событий и говорить об их вероятности.

4. В ящике лежат три не различимых на ощупь шара: красный, синий и желтый. Из ящика наугад вынимают два шара. Сравните по вероятности следующие события:

Т: В ящике остался красный шар.

М: Среди вынутых шаров нет желтого.

S: Оба вынутых шара одного цвета.

R: В ящике остался желтый шар.

Н: Вынутые шары разного цвета.

N: В ящике осталось два шара.

L: В ящике остался один шар.

5. Приведите собственные примеры достоверных и невозможных событий.

Классическое определение вероятности

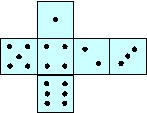Для более точного описания случайных событий нужно научиться измерять их вероятности. Существует несколько подходов к определению вероятностей событий. Сначала рассмотрим так называемый классический подход. Он возник в связи с попытками выявить закономерности в азартных играх, т. е. в таких играх, в которых выигрыш зависит, главным образом, не от умения игрока, а от случайности. Примерами таких игр являются всевозможные игры с игральными кубиками, с подбрасыванием монеты. Игральный кубик (или игральная кость) – это маленький кубик, на гранях (сторонах) которого точками нанесены числа от 1 до 6. В «правильном» кубике сумма чисел на любых противоположных гранях равна 7.

6. а) Сравните события, связанные с бросанием кубика, по их вероятностям:

А: Выпало число 1. F: Выпало число, кратное 3.

В: Выпало число 2. G: Выпало число, меньшее 3.

С: Выпало число 6. Н: Выпало число, большее 3.

D: Выпало четное число. I: Выпало число, кратное 1

Е: Выпало нечетное число. J: Выпало число, большее 3 и меньшее 4

б) Объясните свое решение.

Классический подход к определению вероятности события основан на том, что для события выделяется набор простейших (элементарных) событий – исходов, полностью определяющих условия, при которых происходит или не происходит данное событие. Для любого события, связанного с однократным бросанием кубика, таких взаимоисключающих событий всего шесть: выпадение 1, выпадение 2 и т. д. Все элементарные события – исходы равноправны и потому могут рассматриваться как равновероятные. Тогда вероятность события тем больше, чем больше исходов, при которых оно происходит (благоприятных для него исходов). Например, для события D благоприятны три исхода: выпадение 2, выпадение 4, выпадение 6, а для события G два благоприятных исхода: выпадение 1 и выпадение 2. Таким образом, по классической схеме событие D более вероятно, чем событие G. Самым вероятным является достоверное событие I, оно происходит при любом из 6 возможных исходов.

7. а) Опишите набор элементарных событий при однократном бросании монеты.

б) Какие еще события можно рассмотреть при однократном бросании монеты?

8. а) Опишите набор элементарных событий при двукратном бросании монеты.

б) сравните по вероятности следующие события при двукратном бросании монеты:

V: Оба раза выпадет орел.

W: Оба раза выпадет решка.

U: При первом и втором бросании монета упадет по-разному.

Само количество благоприятных исходов неудобно для выражения вероятности события, поскольку оно зависит от общего количества возможных исходов (элементарных событий), которое в разных ситуациях различно. Например, для однократного бросания монеты достоверное событие имеет 2 благоприятных исхода (из 2 возможных) и столько же благоприятных исходов (но из 6 возможных) имеет относительно маловероятное событие G из задания 6. Чтобы иметь единую шкалу измерения вероятностей принято выражать вероятность не количеством благоприятных исходов, а их долей в общем числе возможных исходов. Например, вероятность выпадения решки (так же как и выпадения орла) при однократном бросании монеты равна (1 благоприятный из 2 возможных исходов). Вероятность обычно принято обозначать буквой Р (от лат. probabilitas – вероятность). Чтобы показать, о вероятности какого именно события идет речь, в скобках около буквы Р записывают букву, обозначающую это событие. Например, запись Р(T) означает вероятность события Т.

Если общее число исходов равно п, а число благоприятных исходов для события Т равно т, то

9. Найдите вероятности всех событий из заданий 6 а) и 8 б).

10. Каковы вероятности невозможного и достоверного событий? В каких пределах может находиться вероятность любого события?

11. В ящике лежат 1красный и 3 зеленых шара (шары отличаются только цветом).

а) Из ящика наугад вынимают один шар. Найдите вероятности следующих событий:

А: вынутый шар окажется зеленым;

В: вынутый шар окажется красным;

С: среди оставшихся в ящике шаров не будет красного;

D: среди оставшихся в ящике шаров не будет зеленого;

Е: среди оставшихся в ящике шаров будет зеленый;

F: среди оставшихся в ящике шаров будет красный.

б) Из ящика наугад вынимают два шара. Найдите вероятности следующих событий:

А: вынутые шары одного цвета;

В: оставшиеся в ящике шары одного цвета;

С: вынутые шары разного цвета;

D: оставшиеся в ящике шары разного цвета.

Статистическое определение вероятности

12. Грани спичечного коробка пронумерованы следующим образом (см. рисунок): передняя – 1, задняя – 6, – верхняя – 3, нижняя – 4, левая – 5, правая – 2.

Событие В1 состоит в том, что при подбрасывании коробка он упадет так, что сверху окажется грань с номером 1. Аналогичным образом определяются события В2, …, В6.

Сравните вероятности: Р(В1), Р(В2), Р(В3), Р(В4), Р(В5), Р(В6).

Можно ли в этом случае пользоваться классическим определением вероятности?

Классическое определение вероятности требует соблюдения весьма жестких условий, главным из которых является равновероятность исходов (элементарных событий). На практике это условие выполняется далеко не всегда. Поэтому получил распространение статистический[1] подход к определению вероятности события, основанный на проведении последовательности (серии) испытаний (опытов), в каждом из которых рассматриваемое случайное событие А может произойти или не произойти. Важно, чтобы каждое испытание проходило в одних и тех же условиях. Результат отдельного испытания называют его исходом. Как и при классическом случае, исходы делятся на благоприятные (событие произошло) и неблагоприятные (событие не произошло). В качестве показателя возможности появления события А принимают отношение числа благоприятных исходов к общему числу испытаний, которое называется частотой события А.

Если в п испытаниях событие А произошло т раз, то частота события А равна .

13. Возьмите полный спичечный коробок и пронумеруйте его грани так, как указано в предыдущем задании.

а) Проведите 5 серий по 10 подбрасываний и для каждой серии найдите частоты событий: В1, В2, В3, В4, В5, В6.

б) Сравните значения частот одних и тех же событий, полученные в разных сериях.

в) Рассмотрите все 50 подбрасываний как одну серию испытаний и найдите частоты тех же событий в этой серии.

Для одного события частоты, получаемые в разных сериях даже с одинаковым количеством испытаний, обычно различаются. Возникает вопрос, как же при этом частоты могут служить мерой возможности появления событий. Чтобы ответить на этот вопрос, надо рассмотреть ситуацию, когда есть возможность соотнести статистический подход с классическим. Например, провести серии испытаний с игральным кубиком или монетой и сравнить полученные частоты событий с вероятностями, определенными для этих событий классическим способом.

14 (лабораторная работа). Определение частоты выпадения «орла» при бросании монеты.

а) Начертите в рабочей тетради такую же таблицу 1.

б) Подбросьте монету 100 раз. В случаях выпадения «орла» делайте отметки значком «+» в соответствующих клетках таблицы.

в) Подсчитайте число т10 благоприятных исходов (количество выпадений «орла») в первых 10 опытах. Впишите значение т10 в соответствующую клетку таблицы. Подсчитайте число т20 благоприятных исходов в 20 опытах. Для этого добавьте к т10 число благоприятных исходов в опытах с 11-го по 20-й. Впишите значение т20 в соответствующую клетку таблицы. Продолжайте обработку результатов опытов, подсчитывая последовательно число благоприятных исходов в 30 опытах т30, в 40 опытах т40 и т. д. до т100 включительно и внося эти числа в таблицу.

г) Впишите в соответствующие ячейки таблицы частоты выпадения «орла», полученные при различном числе опытов: ; ; …; .

Таблица 1

д) Начертите в рабочей тетради таблицу частот (таблицу 2). Перенесите в нее из таблицы 1 значения частоты для различного числа опытов, предварительно переведя их в десятичные дроби (с целью удобства сравнения) и округлив до сотых. При расчетах используйте микрокалькулятор.

Таблица 2

е) Объединитесь в группы по 4 – 5 человек. Познакомьтесь с результатами друг друга. Велико ли, по вашему мнению, различие полученных значений частоты выпадения «орла».

Начертите в тетради таблицу 3. Сравните таблицы 2, полученные разными участниками вашей группы. Для 10, 20, …, 100 опытов найдите наибольшее и наименьшее из полученных значений частот и впишите их в соответствующие клетки таблицы 3.

Под разбросом частот при заданном числе опытов будем понимать разность между наибольшим и наименьшим значениями частоты. Вычислите разброс частот при различном числе опытов и впишите в последнюю строку таблицы 3.

Таблица 3

Как зависит разброс частот от числа испытаний?

Сравните значения частот, приведенные в таблице 2 с классической вероятностью выпадения орла.

Если вероятность события может быть определена классическим способом, то с ростом числа испытаний около нее стабилизируются и значения частоты данного события. Таким образом, при достаточно большом числе испытаний частота события служит хорошим приближением его вероятности. Это дает основание и в случае, когда классическое определение вероятности события невозможно, принять в качестве приближенного значения вероятности частоту события (если число испытаний достаточно велико). Вероятность, полученную таким способом, называют статистической вероятностью.

15. Проведите серию из 100 испытаний для определения статистических вероятностей выпадения чисел 1, 2, 3, 4, 5, 6 при бросании игрального кубика. Сравните полученные значения с классическими вероятностями.

16. На рисунке показана мишень для стрельбы.

В результате выстрела возможны следующие события: А0 – пуля не попала в мишень; А6 – попадание в область, обозначенную цифрой 6; А7 – попадание в область, обозначенную цифрой 7; … ; А10 – попадание в десятку.

Стрелок произвел 50 выстрелов по мишени. Его результаты показаны в таблице.

а) Найдите для данного стрелка статистические вероятности событий А0, А6, А7, А8, А9, А10. Чему равна сумма всех этих вероятностей? Почему?

б) Найдите статистические вероятности следующих событий:

1) попадание в десятку;

2) непопадание в десятку;

3) попадание в мишень;

4) непопадание в мишень;

5) попадание в «яблочко» (область, закрашенную черным цветом);

6) непопадание в «яблочко».

в) Найдите суммы статистических вероятностей событий 1) и 2), событий 3) и 4), событий 5) и 6). Объясните полученный результат.

Частоты событий можно наглядно показать с помощью столбчатой диаграммы. На такой диаграмме по горизонтальной оси указываются рассматриваемые события, а по вертикальной оси откладываются их частоты.

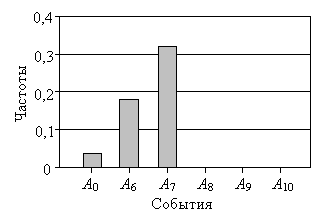17. На рисунке приведен фрагмент столбчатой диаграммы частот (статистических вероятностей) для событий А0, А6, …., А10 из задания 208. Перенесите этот фрагмент в рабочую тетрадь. Достройте диаграмму. Чему равна сумма высот всех столбцов диаграммы?

18. По данным таблицы 2 из задания 16 постройте столбчатую диаграмму для частот выпадения решки при 10, 20, 30,…, 100 бросаниях монеты. С помощью диаграммы убедитесь в том, что с ростом числа бросаний частоты выпадения стабилизируются около вероятности выпадения решки, определяемой классическим способом.

Существует еще один наглядный способ представления частот событий – в виде круговой диаграммы. Если несколько случайных событий образуют полную группу, т. е. никакие другие события в рассматриваемой ситуации невозможны, то, как вы могли убедиться, сумма частот этих событий в серии опытов равна 1. При построении круговой диаграммы частот за единицу принимают площадь какого-нибудь круга. Тогда каждому событию соответствует сектор этого круга, площадь которого равна частоте события. Площадь сектора пропорциональна углу между заключающими его радиусами круга. Поэтому чтобы «вырезать» сектор, соответствующий частоте Р, нужно построить угол с вершиной в центре круга и градусной мерой 360°×Р. Обычно для наглядности разные секторы круговой диаграммы закрашивают разными цветами.

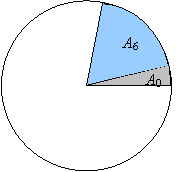19. На рисунке приведен фрагмент круговой диаграммы частот, построенный по приведенным выше результатам стрельбы. Перенесите рисунок в тетрадь. Достройте диаграмму.

20. По результатам задания 13 постройте столбчатую и круговую диаграммы частот выпадения различных граней при 50 бросаниях спичечного коробка.

Из истории математики

В настоящее время теория вероятностей широко применяется во всех естественных науках – физике, химии, биологии. Без применения вероятностных методов невозможно создание и испытание самолетов, космических кораблей, компьютеров и других сложнейших технических устройств, от которых требуется высочайшая надежность и безопасность. ор этого круга, площадь которого равна частоте события. Но применение теории вероятностей не ограничивается перечисленными областями знания. Она все глубже проникает и в гуманитарные, социально-экономические науки.

А начиналась теория вероятностей совсем с другого – с попыток выявить закономерности в азартных играх, т. е. в таких играх, в которых выигрыш зависит, главным образом, не от умения игрока, а от случайности. Анализом азартных игр с точки зрения математики занимались, например, крупнейшие французские ученые XVII в. Блез Паскаль и Пьер Ферма. С тех пор при изучении теории вероятностей продолжают широко использоваться модели, основанные на подбрасывании игрального кубика, монеты, вытаскивании шаров из ящика и т. п.

В развитие теории вероятностей значительный вклад внесли российские математики – (1903 – 1987), (1856 – 1922) и многие другие.

Выполните задания.

21. Приведите пример трех событий, связанных с бросанием игрального кубика, так чтобы первое было менее вероятно, чем второе, а второе – менее вероятно, чем третье.

22. а) Какие из следующих событий равновероятны:

1) выпадение четного числа при бросании игрального кубика;

2) выпадение единицы или двойки при бросании игрального кубика;

3) вытаскивание наугад черного шара из ящика, в котором лежит один белый, один черный и один зеленый шар, различающиеся только цветом;

4) выпадение решки при бросании монеты;

5) выпадение двух орлов при бросании двух монет.

б) Приведите свой пример равновероятных событий.

23. Игральный кубик бросили один раз. Какова вероятность следующих событий:

Т: сумма чисел на всех боковых гранях равна 14;

L: сумма чисел на всех боковых гранях равна 15;

G: числа на верхней и нижней гранях отличаются на 3;

K: числа на верхней и нижней гранях отличаются на 4.

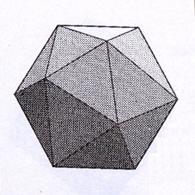24. Икосаэдром называется геометрическое тело, которое имеет двадцать граней, представляющих собой одинаковые равносторонние треугольники. Представьте себе, что у икосаэдра занумеровали все грани числами от 1 до 20 (аналогично тому, как у игрального кубика грани занумерованы числами от 1 до 6). Будем считать, что при бросании «игрального икосаэдра» выпадает то число, которое оказывается на его нижней грани. Найдите вероятности следующих событий при бросании «игрального икосаэдра»:

1) выпадение числа 17;

2) выпадение четного числа;

3) выпадение простого числа;

4) выпадение числа, кратного числу 3;

5) выпадение числа, кратного числу 4;

6) выпадение числа, кратного 4, но не кратного 3;

7) выпадение числа, кратного 4, но не кратного 3.

25. В ящике находятся несколько отличающихся только цветом шаров: 5 черных, 7 белых и 10 красных. Какова вероятность, что взятый наугад из ящика шар окажется белым?

26. В ящике находятся 1 белый и 3 черных шара (шары отличаются только цветом). Из ящика берут наугад 3 шара. Событие A состоит в том, что все выбранные шары будут черными, событие В – в том, что среди выбранных шаров окажется белый.

а) Попробуйте, на вычисляя вероятностей р(А) и р(В) по отдельности, найти их сумму;

б) Найдите вероятности р(А) и р(В) и проверьте ваше предположение об их сумме.

27. В каждом из двух ящиков находится по одному белому и одному черному шару. Из каждого ящика берут наугад по одному шару и перекладывают в другой ящик. Какова вероятность, что после перекладывания в одном из ящиков будут только белые шары, а в другом – только черные?

28. На автобусной остановке останавливаются автобусы трех маршрутов: № 7, № 26 и № 64. Всего работает 8 автобусов № 7, 10 автобусов № 26 и 5 автобусов № 64. Пассажир ждет на остановке автобус № 7 или № 64. Какова вероятность того, что первым подойдет нужный автобус?

29. а) Атос, Портос, Арамис и Д’Артаньян нашли золотую монету и решили разыграть ее. Как организовать справедливый розыгрыш монеты между друзьями (так, чтобы у каждого шансы на выигрыш были одинаковы)? Ничего, кроме самой монеты, использовать для розыгрыша нельзя.

*б) Атос, Портос и Арамис нашли золотую монету и решили разыграть ее между собой. Как это сделать, не пользуясь ничем, кроме этой монеты, чтобы розыгрыш был справедливым?

30. Пусть «о» – выпадение орла, «р» – выпадение решки при однократном бросании монеты. Монету подбрасывают 4 раза. Какой результат более вероятен: «оооо», «рррр», «оорр» или «орор»?

31. В старину среди морских разбойников – пиратов были очень популярны различные игры в кости. Например, игра «чет – нечет»:

Два игрока бросают кость (игральный кубик) по очереди. Если сумма чисел, выпавших в двух бросаниях, четная, то выигрывает первый игрок, если нечетная – второй.

Проигравший отдавал победителю мешок золотых монет.

Однажды пират Билли Бонс сказал капитану Флинту, что придумал новую игру, и предложил сыграть в нее. «Давай, бросим кость по очереди. Если произведение выпавших чисел окажется четным, выигрываю я, если нечетным – ты».

Согласились бы вы на месте Флинта играть в такую игру?

*32. Трамвайные билеты имеют шестизначные номера с 100 000 по 999 999. Какова вероятность того, что:

1) пассажиру попадется билет, в номере которого число, образованное первыми тремя цифрами, такое же, как число, образованное последними тремя цифрами;

2) пассажиру попадется билет, номер которого слева направо читается так же, как справа налево.

33. Известно, что разные буквы встречаются в текстах не одинаково часто.

а) Определите частоты появления разных букв на странице какой-нибудь книги и покажите их на столбчатой диаграмме.

б) Определите частоты гласных и согласных букв и покажите их на круговой диаграмме.

в) Сравните свои результаты с результатами, полученными другими учащимися.

[1] Статистический – означает «связанный с массовыми случайными явлениями».