НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ЭНЕРГЕТИКИ
КАФЕДРА ТЕХНИКИ И ЭЛЕКТРОФИЗИКИ ВЫСОКИХ НАПРЯЖЕНИЙ
“УТВЕРЖДАЮ”
Декан ФЭН
“___ ”______________200 г.
РАБОЧАЯ ПРОГРАММА учебной дисциплины
«ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
ООП 140200 "Электроэнергетика" - бакалавр
Факультет энергетики
Курс 2, семестр 4
Лекции 51 час
Практические занятия 34 часа
Расчетно-графическая работа – 4 семестр
Самостоятельная работа 43 часа
Экзамен – 4 семестр
Всего 128 часов
Новосибирск
2006
Рабочая программа составлена на основании Государственного образовательного стандарта высшего профессионального образования по направлению 551700 Электроэнергетика.
Регистрационный номер 215 тех/бак, дата утверждения 27 марта 2000 г.
Шифр дисциплины в ГОС – ЕН. Ф.01, федеральный компонент, шифр дисциплины по учебному плану – 2006.
Рабочая программа обсуждена на заседании кафедры Техники и электрофизики высоких напряжений – протокол № _____ от __________________ 200 г.
Программу разработали
профессор, д. т.н.
профессор, д. т.н.
Заведующие кафедрой
доцент, к. т.н.
профессор, д. т.н.
Ответственный за основную
доцент, к. т.н.
1. Внешние требования
Подготовка специалиста по направлению «Электроэнергетика» требует от него на всех направлениях будущей работы (научно-исследовательской, проектной, в эксплуатации электрических сетей) умения определять вероятностные характеристики как показателей режимов электрических сетей и характеристик электроснабжения потребителей, так и статистические характеристики тех воздействий, которым подвергается электроэнергетическое электрооборудование в условиях эксплуатации: в нормальном эксплуатационном режиме и в аномальных штатных и нештатных ситуациях. Это требование обуславливает необходимость уметь оценивать вероятностные характеристики более сложных событий на основе вероятностно-статистических характеристик как самого оборудования, так и более простых событий, являющихся составными частями более сложного события. Любое электрооборудование в электрических сетях выбирается с учетом определенной вероятности его отказа, которая должна быть достаточно малой. Курс «Теория вероятностей и математическая статистика» (ТВиМС) является фундаментальным курсом, на основе которого могут быть решены задачи, связанные с надежностью эксплуатации электрических сетей и электрооборудования, установленного на электрических станциях и подстанциях.
2. Особенности (принципы) построения дисциплины
Особенности (принципы) построения дисциплины описываются в табл. 1.
Таблица 1
Особенности (принципы) построения дисциплины
Особенность (принцип) | Содержание |
Основание для введения курса. | Цикл ЕН ГОС ВПО подготовки дипломированного специалиста по направлению «Электроэнергетика», «Математика» |
Адресат курса | Бакалаврская подготовка по направлению 551700 «Электроэнергетика» |
Главная цель | Применение ТВ и МС при решении ряда задач, связанных с обеспечением надежной эксплуатации электроэнергетического оборудования |
Ядро курса | Основные теоремы теории вероятностей и основы математической статистики, необходимой для грамотной обработки исходных данных, получаемых от электротехнических заводов и от эксплуатирующих организаций |
Уровень требований по сравнению с ГОС | Содержание задач, по-возможности, охватывает также и некоторые задачи электротехники и электроэнергетики |
Объём курса в часах | 128 часов |
Описание основных "точек" (понятий) | - Понятие вероятности события - Понятие случайной величины (СВ) - Понятие случайного процесса - Теоремы сложения и умножения вероятностей - Законы распределения вероятностей случайных величин (одномерных и двумерных) - Числовые характеристики СВ - Законы распределения функций СВ - Точечные и интервальные статистические оценки числовых характеристик СВ - Проверка правдоподобия гипотез и уровни значимости |
3. Цели учебной дисциплины
Цели учебной дисциплины описываются в табл.2.
Таблица 2
После изучения дисциплины студент будет
Номер цели | Содержание цели |
иметь представление | |
1 Ниша применения полученных знаний | Выделение комплекса задач электроэнергетики, в которых применяются знания, полученные при изучении курса ТВиМС |
знать | |
2. Случайные события | Понятия случайных событий, основные теоремы |
3.Случайные величины | Понятие СВ и их вероятностных характеристик |
4. Случайные процессы | Понятие случайных процессов и их основных характеристик |
5. Основы математической статистики | Оценка основных вероятностных характеристик случайных событий и случайных величин с определенной степенью достоверности |
уметь | |
6. Определять вероятности сложных событий на основе известных вероятностных характеристик простых событий, составляющих сложное событие | Определение вероятности сложных событий, имеющих место при эксплуатации электрических сетей и их элементов |
7. Уметь на основе известных законов распределения вероятностей случайных величин определять их числовые характеристики | Определение числовых характеристик случайных величин, позволяющих произвести упрощенную оценку вероятностных свойств случайной величины |
8. Определять закон распределения функции случайных величин при известных законах распределения этих случайных величин | Такая постановка задачи очень часто встречается в задачах электроэнергетики, так как в ряде случаев известны законы распределения СВ, требуется же определить закон распределения функции этих СВ, относительно которой нельзя поставить непосредственный статистический эксперимент |
9. Определять вероятностные характеристики случайных процессов | В задачах электроэнергетики специалист встречается с необходимостью обработки случайных процессов( например, определения основных характеристик случайного изменения напряжения на шинах питающих подстанций). |
10. Грамотно обрабатывать исходный статистический материал | Получать достоверную статистическую информацию на основе мониторинга, регистрации и активных экспериментов в электрических системах |
4. Содержание и структура учебной дисциплины
Блок, модуль, раздел, тема | Часы | № цели |
Лекции (51час) | ||
Блок 1 . Теория вероятностей | ||
Введение. Цель и задачи раздела курса. Применение ТВ при решении практических задач из области электротехники и электроэнергетики | 1 | 1 |
Основные понятия теории вероятностей События. Классификация событий (достоверное, невозможное, равносильные, равновозможные, произведение событий, сумма событий, геометрическая интерпретация произведения и суммы событий, противоположные, полная группа событий, случаи. Понятие вероятности события. Классическое определение вероятности (для равновозможных событий). Статистическое определение вероятности. Определение вероятности – как степень уверенности познающего субъекта. Классическое определение вероятности события. Элементы комбинаторики. | 2 | 2, 6 |
Основные теоремы теории вероятностей Постановка задачи. Теорема умножения вероятностей. Теорема сложения вероятностей. Примеры на применение теорем умножения и сложения вероятностей 1.Разработка более надежных систем из менее надежных элементов 2. Вероятностно-надежностные характеристики сложных систем 3. Зависимые события Формула полной вероятности Теорема гипотез (формула Байеса) | 4 | 2,6 |
Последовательность независимых испытаний - Частная теорема о повторении опытов. Схема Бернулли. - Интегральная предельная теорема - Асимптотическая формула Пуассона - Общая теорема о повторении опытов | 2 | 2, 6 |
Случайные величины - Непрерывные и дискретные случайные величины (СВ) - Законы распределения вероятностей СВ. Ряд распределения. Функция распределения и её свойства. Вероятность попадания непрерывной СВ на заданный участок - Плотность распределения вероятностей непрерывной СВ и её свойства - Числовые характеристики СВ - Характеристики положения: математическое ожидание, мода, медиана. - Моменты СВ. Начальные и центральные моменты. Дисперсия и среднее квадратическое значение СВ. Коэффициент асимметрии. Эксцесс СВ. | 4 | 3, 7 |
Некоторые законы распределения СВ 1. Законы распределения дискретных СВ 1.1. Биномиальный закон 1.2. Закон Пуассона ( редких явлений) 2. Законы распределения непрерывных СВ 2.1. Экспоненциальный закон 2.2. Закон равномерной плотности 2.3. Нормальный закон распределения 2.4. Усеченный нормальный закон | 4 | 3, 7 |
Системы случайных величин 1. Функция распределения системы непрерывных СВ и её свойства 2. Плотность распределения вероятностей системы двух СВ и её свойства 3. Условные законы распределения. Законы распределения СВ, входящих в систему 4. Числовые характеристики системы СВ. Начальные и центральные моменты системы СВ. Корреляционный момент и коэффициент корреляции. Линии регрессии. Корреляционные отношения. 5. Некоторые законы распределения системы СВ 5.1. Закон равномерной плотности 5.2. Нормальный закон на плоскости. Эллипсы рассеивания. | 6 | 3, 7 |
Законы распределения функций СВ 1. Постановка задачи 2. Числовые характеристики функций СВ 3. Определение закона распределения функции одного случайного аргумента 3.1. Функция 3.2. Функция 3.3. Функция 4. Определение закона распределения функции двух случайных аргументов 4.1. Постановка задачи 4.2. Определение закона распределения суммы двух случайных величии. Композиция законов распределения. | 4 | 3, 8 |
Теоремы о числовых характеристиках СВ | 2 | 3, 7, 8 |
Предельные теоремы теории вероятностей 1. Характеристические функции СВ и их свойства 2. Неравенство Чебышева 3. Теоремы Чебышева 4. Теорема Бернулли | 2 | 3,7, 8 |
– монотонно возрастающаяБлок 2 . Основы теории случайных процессов | ||
Основные понятия случайных процессов ( СП) 1. Случайные процессы и их характеристики 2. Начальные и центральные моменты СП. Автокорреляционная функция СП. 3. Основные свойства математического ожидания и автокорреляционной функции СП | 2 | 4 |
Классификация СП 1. Стационарные СП Стационарность в узком и широком смыслах. 2. Нормальные процессы 3. Марковские процессы. 4. Основные задачи решаемые с помощью теории СП | 1 | 4, 9 |
Спектральная плотность стационарных случайных процессов Линейные преобразования стационарных случайных процессов при использовании понятия спектральной плотности | 4 | 4, 9 |
Решение задачи фильтрации помехи | 1 | 4, 9 |
Блок 3 . Основы математической статистики | ||
Основные задачи и понятия математической статистики Статистические законы распределения СВ | 1 | 1, 10 |
Статистические оценки числовых характеристик СВ 1. Точечные оценки и требования к их определению (состоятельность, несмещенность и эффективность) 2. Интервальные оценки. Доверительная вероятность и доверительный интервал | 2 | 5,10 |
Проверка правдоподобия гипотез 1. Критерий значимости гипотезы 2. Критерий принадлежности двух статистических выборок единой генеральной совокупности 2.1. Порядковый критерий Вилькоксона 2.2. Критерий равенства математических ожиданий (критерий Z) 3. Проверка гипотезы о виде закона распределения СВ 3.1. Критерий Пирсона ( 3.2. Критерий Колмогорова 3.3. Критерий Мизеса (n | 6 | 5, 10 |
Основы теории статистической корреляции 1. Оценка числовых характеристик двух СВ по данным статистической выборки 2. Проверка гипотезы об отсутствии корреляции между двумя СВ, входящими в систему 3. Определение доверительного интервала для коэффициента корреляции | 3 | 5,10 |
)
)Практические занятия по разделу «Теория вероятностей» (34 часа) | ||
Основные понятия. Сумма и произведение событий. Запись сложных событий через составляющие его простые события. Классическое определение вероятности события для схемы случаев. | 2 | 2, 6 |
Основные теоремы теории вероятностей (теоремы умножения и сложения) | 2 | 2, 6 |
Формула полной вероятности и теорема гипотез. | 2 | 2, 6 |
Последовательность независимых испытаний. Частная и общая теоремы о повторении опытов. Интегральная предельная теорема Асимптотическая формула Пуассона | 2 | 2.6 |
Функция и плотность распределения вероятностей случайной величины | 2 | 3, 7 |
Числовые характеристики случайной величины | 2 | 3, 7 |
Некоторые законы распределения вероятностей случайной величины (закон Пуассона, закон равномерной плотности, нормальный закон) | 2 | 3, 7 |
Системы случайных величин. Зависимые и независимые СВ. Числовые характеристики системы дискретных и непрерывных СВ. Определения вероятности попадания двух СВ в заданные области при законах распределения равномерной плотности и нормальном. | 6 | 3, 7 |
Функции случайных величин. Числовые характеристики функций СВ. Законы распределения функций СВ | 4 | 3, 7 |
Случайные процессы. Числовые характеристики СП. Линейные преобразования СП при использовании понятия спектральной плотности процесса | 4 | 4, 9 |
Основы математической статистики. Выполняется расчетное задание. Состав задания Заданы две независимые выборки случайных чисел, распределенных по нормальным законам. 1. Определить статистические оценки математического ожидания и дисперсии двух выборок 2. Проверить правдоподобие гипотезы о принадлежности двух выборок единой генеральной совокупности с помощью трех критериев: порядкового критерия Вилькоксона, равенства математических ожиданий и равенства дисперсий (критерий Фишера). 3. Если гипотеза о принадлежности двух выборок единой генеральной совокупности не противоречит располагаемому статистическому материалу, то объединить выборки и определить точечные оценки математического ожидания и дисперсии для объединенной выборки 4. Найти интервальные оценки при доверительной вероятности Рдов=0.95 для статистическтх оценок МО и дисперсии объединенной выборки 5. Проверить гипотезу о нормальности закона распределения объединенной выборки по критериям: Пирсона и Мизеса. Определить уровни значимости гипотезы о нормальности закона объединенной выборки по этим двум критериям. 6. Построить гистограмму для объединенной выборки и нанести на график плотность распределения по гипотетическому нормальному закону 7. Рассмотреть далее заданные две выборки как систему двух случайных величин. На основе корреляционной таблицы определить оценки математических ожиданий и дисперсий для двух выборок, а также определить оценку коэффициента корреляции между двумя СВ. 8. Проверить гипотезу об отсутствии корреляционной связи между двумя СВ и определить уровень значимости этой гипотезы 9. Если гипотеза об отсутствии корреляционной связи между двумя СВ противоречит располагаемому статистическому материалу, то определить доверительный интервал для оценки коэффициента корреляции при Рдов=0.95. 10. Составить пояснительную записку к выполненному расчетному заданию с четкими выводами по каждому из его пунктов. | 6 | 5, 10 |
5. Учебная деятельность
1. По всем темам практических занятий каждый студент выполняет индивидуальные задания.
2. По желанию студент может выполнять расчетные задания на предложенную им тему, содержание которой охватывает приведенную в таблице тематику и включает в себя какую-либо практическую задачу из области электроэнергетики.
3. Требования к оформлению пояснительной записки к расчетному заданию
3.1. Пояснительная записка выполняются на стандартных листах бумаги формата А4.
3.3. Гистограмма приводится на графике. Желательно компьютерное оформление как самой пояснительной записки, так и её графического сопровождения.
6. Правила аттестации студентов по учебной дисциплине
1. В течение семестра студенты аттестуются по трехбалльной системе (0, 1, 2) на 7 и 12 неделях семестра.
2. К экзамену допускаются студенты, выполнившие все индивидуальные задания и сдавшие в оформленном виде расчетное задание.
3. В экзаменационном билете содержится один теоретический вопрос (по любому из трех разделов курса) и две задачи (по разделу «Теория вероятностей» - одна из задач на тему «Функции случайной величины»).
7. Список литературы
Основной список
1. Теория вероятностей (любого года издания)
2. Теория вероятностей и математическая статистика: - М.: Высшая школа.-2005.- 479 с.
3. , , Теория вероятностей и её приложения к задачам электроэнергетики.-СПб.: Наука.-1992.-376 с.
4. , Теория вероятностей и математическая статистика. Сборник задач по разделу «Теория вероятностей».- НГТУ.-2006.- 111 с.
5. , Основы математической статистики. Методические указания к расчетному заданию.-НГТУ.-1999.-34 с.
. Дополнительный список
1. Дунин-, Теория вероятностей и математическая статистика.- М.: Гостехизщдат.-1955.- 301 с.
Также могут быть рекомендованы любые другие учебники и учебные пособия по Теории вероятностей и математической статистике.
8. Контролирующие материалы для аттестации студентов по дисциплине
Экзамен (третий семестр), оценка по пятибалльной системе
Экзаменационные теоретические вопросы
Раздел: Теория вероятностей
1. Поясните следующие понятия: событие, случайная величина, случайный процесс. Охарактеризуйте вероятностные описания этих понятий и приведите соответствующие примеры.
2. Классификация событий. Поясните понятия произведения и суммы событий. Приведите соответствующие примеры.
3. Теоремы умножения и сложения вероятностей событий. Совместные и несовместные события. Зависимые и независимые события. Приведите соответствующие примеры.
4. Формула полной вероятности для событий. Поясните её применение на каком-либо примере.
5. Теорема гипотез применительно к событиям. Поясните её применение на каком-либо примере.
6. Частная и общая теоремы о повторении опытов. Проиллюстрируйте применение этих теорем на конкретных примерах.
7. Интегральная предельная теорема применительно к задаче о повторении независимых испытаний. Поясните её применение на конкретном примере.
8. Использование асимптотики Пуассона при решении задачи о повторении независимых испытаний. Ниша использования асимтотики Пуассона. Поясните применение асимптотики на конкретном примере.
9. Случайные величины и их классификация. Виды задания законов распределения вероятностей непрерывных и дискретных случайных величин. Приведите примеры.
10. Характеристики положения и моменты случайных величин. Приведите примеры определения математического ожидания и дисперсии непрерывной или дискретной случайной величины.
11. Законы распределения дискретных случайных величин( биномиальный и закон Пуассона) и их свойства. Составьте задачу на применение какого-либо из этих законов.
12. Законы распределения непрерывных случайных величин. Основные характеристики закона равномерной плотности, нормального и усеченного нормального законов. Составьте пример на применение какого-либо из этих законов.
13. Системы случайных величин. Закон распределения вероятностей системы двух случайных величин. Зависимые и независимые случайные величины. Условные и безусловные законы распределения. Приведите пример определения безусловного и условного законов распределения.
14. Числовые характеристики системы случайных величин (моменты первого и второго порядков). Приведите пример определения математического ожидания, дисперсии и корреляционного момента системы двух непрерывных или дискретных случайных величин.
15. Закон равномерной плотности на плоскости. Составьте задачу на применение этого закона.
16. Нормальный закон на плоскости. Эллипсы рассеивания. Вероятности попадания случайных величин в эллипс, круг и прямоугольник со сторонами, параллельными осям координат. Составьте задачу на использование нормального закона на плоскости.
17. Законы распределения функций случайных величин. Методика определения законов распределения монотонных и немонотонных функций случайного аргумента.
18. Методика определения закона распределения функции двух случайных величин. Композиция законов распределения.
19. Характеристические функции и их свойства. Что дает применение аппарата характеристических функций? Получите характеристическую функцию для закона равномерной плотности одной случайной величины.
20. Предельные теоремы теории вероятностей. Неравенство и теорема Чебышева. Центральная предельная теорема Ляпунова с примером.
Раздел: Теория случайных процессов
21. Классификация случайных процессов. Свойства стационарных случайных процессов. Стационарность в широком и узком смыслах. Эргодические процессы.
22. Спектральная плотность случайных процессов и её физический смысл. Преобразования Хинчина-Винера.
23. Линейные преобразования стационарных случайных процессов. Использование понятия спектральной плотности. Определение математического ожидания и корреляционной функции процесса на выходе линейной системы.
24. Задачи анализа и синтеза линейных систем. Использование понятия спектральной плотности при решении задачи фильтрации случайной помехи, поступающей на вход линейной системы.
Раздел: Основы математической статистики
25. Точечные и интервальные оценки случайных величин по данным экспериментов. Требования к точечным оценкам. Точечные и интервальные оценки для математического ожидания и дисперсии.
26. Общий алгоритм проверки правдоподобия тех или иных гипотез при обработке статистических данных. Уровни значимости гипотез. Какие критерии и для проверки каких гипотез Вы знаете?
27. Критерии, используемые при проверке гипотезы о принадлежности двух независимых выборок единой генеральной совокупности.
28. Критерии, используемые при проверке гипотезы о виде закона распределения случайной величины.
Тематика задач, содержащихся в экзаменационных билетах
Задача № 1
1. Упростить, пользуясь геометрической интерпретацией событий некоторое более сложное событие
2. Определить вероятности замыкания или размыкания цепи, содержащей несколько контактов, соединенных последовательно – параллельно. Вероятность замыкания (размыкания) единичного контакта задана.
3. Задачи на теорему полной вероятности события и на теорему гипотез.
4. Задан закон распределения некоторой случайной величины. Определить вероятность некоторого события (например, вероятности попадания в определенный интервал).
5. При заданных условиях построить ряд распределения и функцию распределения дискретной СВ.
6. Задан закон распределения системы СВ. Определить вероятность попадания Х и Y в некоторую заданную область
7. Некоторая случайная величина является суммой большого числа независимых одинаково распределенных слагаемых. Заданы математическое ожидание и дисперсия слагаемого. Определить закон распределения их суммы.
8. Задан закон распределения двух независимых одинаково распределенных сомножителей. Определить математическое ожидание и дисперсию их произведения.
9. Заданы функциональные связи двух СВ U и V со случайными величинами Х и Y. Определить KUV и rUV.
10. Задана корреляционная таблица для двух СВ. Определить числовые характеристики: M[X], M[Y], D[X], D[Y], KXY, rXY
Задача № 2
Все задачи на определение закона распределения функции одной случайной величины.
Заданы: 
, закон распределения аргумента (
или 
).
Найти: закон распределения функции (
и 
).
Контролирующие материалы для проверки остаточных знаний
1. Охарактеризуйте понятия: «Случайные события», « Случайные величины», «Случайные процессы»
2. Какие события называются совместными (несовместными)?
3. Какие события называются независимыми (зависимыми)?
4. Как определяется ве6роятность некоторого события, если события являются случаями?
5. Сформулируйте теоремы сложения и умножения вероятностей.
6. Как определятся вероятность некоторого события, которое может происходить одновременно с какими-либо другими событиями, называемыми гипотезами?
7. Что такое доопытная и послеопытная вероятности некоторого события?
8. Если в каждом опыте вероятности появления некоторого события одинаковы, то как определить вероятность того, что в серии из n опытов это событие произойдет m раз?
9. Что такое дискретные и непрерывные величины?
10. Какие числовые характеристики случайных величин Вы знаете?
11. Какие формы законов распределения вероятностей дискретных случайных величин вы знаете?
12. Какие формы законов распределения вероятностей непрерывных случайных величин вы знаете?
13. Охарактеризуйте закон равномерной плотности и нормальный закон распределения вероятностей.
14. Если Вам задан закон распределения системы двух случайных величин, то как Вы определите вероятность попадания этих СВ в заданную область на плоскости?
15. Если Вам задана функциональная связь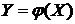 
и задан закон распределения вероятностей аргумента Х, то как вы определите закон распределения функции Y?
16. Что такое статистические оценки вероятностей случайной величины?
17. Какие основные требования Вы предъявляете к статистическим оценкам математического ожидания случайной величины и её дисперсии?
18. Что Вы понимаете под уровнем значимости той или иной гипотезы относительно закона распределения вероятностей случайной величины?
19. Назовите какие критерии проверки той или иной гипотезы относительно закона распределения вероятностей случайной величины Вы знаете.
20. Какие вероятностные характеристики для описания случайного процессы Вы знаете?
21. Поясните свойства стационарного процесса
22. Что такое Марковские случайные процессы?
