Глава 6. Рынок долгосрочного заемного капитала

<Для подсчета доходности к погашению сначала используется формула приведенной стоимости, подставляются цифры, но считается ответ по приближенной формуле>

Задание 4

Две облигации А и С имеют номинал 1000 долларов, купонную ставку равную 10% и продаются по рыночной стоимости, которая обеспечивает одинаковую доходность к погашению - 9 %. Однако у облигации А срок до погашения составляет 15 лет, а у С - 5 лет. Рассчитайте рыночную стоимость этих облигаций. Поясните, почему, несмотря на равную доходность, их рыночные стоимости отличаются?

1)  для А:

→

2) аналогично для С: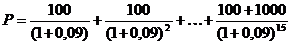

3) отличие - из-за различия сроков погашения.

Задание 5

Инвестор купил облигацию с 10 процентным полугодовым купоном за 95 процентов от номинала. Какова доходность к погашению, если облигация погашается через три года.

1) →

2) упрощенная формула: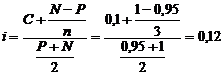

Задание 6

Инвестиционная компания купила облигацию с 10 процентным годовым купоном по курсу 79.96. Номинальная стоимость облигации - 1000 долларов, выплата купонов раз в квартал. Какова доходность к погашению, если облигация погашается через 5 лет.

---- аналогично предыдущей -----

Задание 7

Компания «А» приобрела облигацию номинальной стоимостью 100'000 руб., купонной ставкой 20% годовых с начислением процентов в конце каждого года, сроком до погашения 10 лет, по цене 70’000 руб. Определите значение доходности к погашению и значение текущей доходности на момент приобретения облигации.

1)  доходность к погашению считается аналогично предыдущим двум задачам

2)  текущей доходности на момент приобретения облигации:

Задание 8

Компания «А» приобрела облигацию номинальной стоимостью 10'000 руб., купонной ставкой 20% годовых с начислением процентов в конце каждого квартала, сроком до погашения 5 лет, по цене 9’500 руб. Определите значение доходности к погашению на момент приобретения облигации.

----- аналогично задачам 4-5 -----

Задание 9

Коммерческий банк имеет два альтернативных варианта использования денежных средств:

А) Выдать кредит в сумме 800’000 руб. под 20% годовых (начисляются простые проценты) на срок – 180 дней;

Б) Приобрести облигацию номинальной стоимостью 1’000’000 руб. с дисконтом 10% от номинальной стоимости, сроком до погашения 180 дней, купонной ставкой 10% годовых, периодичность выплаты – по полугодиям, последний купон выплачивается при погашении облигации вместе с номинальной стоимостью.

1) доход от кредита: →880000-800000=80000

2) доход от облигаций: →1000000-950000 (т. к. куплено c 5% дисконтом за 180%)=50000 → кредит выгоднее.

Задание 10

Какой из вышеперечисленных вариантов, при прочих равных условиях, обеспечит банку наибольшую эффективность использования денежных средств?

Задание 11

Компания «Next» выпустила 1 января 1989 года облигации номиналом 1000$, купонной ставкой 8%, сроком погашения 10 лет и полугодовым начислением процентов (30 июня и 31 декабря).

А) Рассчитайте полную доходность облигации на 1 января 1989 года.

Б) Определите полную доходность облигации на 1 января 1996 года, если текущая рыночная цена равна а) 825$, б) 1107$. Объясните динамику общей доходности облигации.

В) Чему равна текущая доходность в каждом случае?

Г) Приобрели бы вы 1 января 1996 года облигацию компании «Next», если бы уровень процентной ставки а) упал до 10%, б) возрос до 15%. Поясните ваш ответ.

1) (раз без дисконта – паритетная облигация à купонная ставка равна рыночной процентной ставке à i=0,08)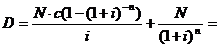

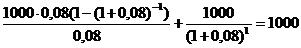
2)→,

.

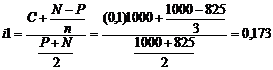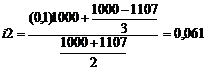3) ,

4)

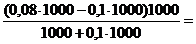
Задание 12

Облигация со сроком до погашения 4 года, номинальной стоимостью 1000$ и купонной ставкой 10%, продается по цене 1032,40$. По ней полагаются ежегодные процентные выплаты.

А) Чему равна доходность к погашению данной облигации?

Б) Определите доходность облигации, если она будет отозвана через 2 года по цене 1100$.

1) Отсюда высчитывается доходность к погашению r. Посчитаем ее по упрощенной формуле: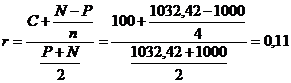

2)

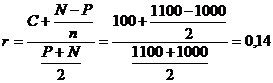
Задание 13

Срок до погашения облигации - 90 дней, номинал - 1000 рублей, сумма по последнему купону (выплачивается в момент погашения облигации) составляет 100. Определите текущую стоимость облигации, если ставка дисконтирования равна 8 % годовых (формула простых процентов), дней в году - 360.

1)

Задание 14

Номинал облигации – 1000 долларов. Купонная ставка – 8 %. Купон выплачивается два раза в год. Цена покупки дилера – 112:03, цена продажи дилера – 112:07. Время до погашения 1 год. Рассчитать текущую доходность и доходность к погашению.

1)  Рассчитываем для инвестора (беря цену его покупки 112.07)

2)  текущая доходность (1000$ = 100 пунктов):

3)  доходность к погашению (по упрощенной формуле):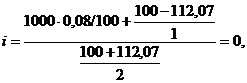

4)  годовая доходность дилера: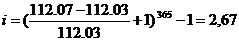

Задание 15

Номинал дисконтной облигации - 1 000 000 долларов. Одна облигация куплена за 92,75 , срок погашения через 112 дней, вторая за 94,86, срок погашения – 103 дня. Какую облигацию приобретет инвестор?

1)  доходность к погашению 1-й облигации:

2)  доходность к погашению 2-й облигации:

→ 1-я облигация выгоднее.