УДК 622.276.031.532.11
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ТЕПЛОПЕРЕДАЧИ В СТВОЛЕ НЕФТЯНЫХ СКВАЖИН
1, Аб. Г. Рзаев1, 2, Ас. Г. Рзаев1, 2, 2
(Институт систем управления НАНА1,
Азербайджанская государственная нефтяная академия2)
Как известно, при движении пластовых флюидов (нефти, газа и воды) в подъемной насосно-компрессорной трубе (НКТ) от забоя до устья нефтедобывающей скважины (НС) происходит постепенное понижение температуры потока. При этом происходит увеличение вязкости нефти (нефтяной эмульсии), и, следовательно, гидравлического сопротивления (силы трения), возникающего при движении флюидов в НКТ. Понижение температуры потока особенно нежелательно для высоковязких нефтей, содержащих тугоплавкие парафины и структурированные асфальтены (в виде кластеров), так как при этом происходит не только повышение гидравлического (вязкостного) сопротивления, оказываемое потоку, а также отложение этих компонентов на внутренней поверхности НКТ и создающее проблемы в работе глубинного насоса. Следовательно, определение законов распределения температуры восходящего потока флюида (ПФ) в НКТ с учетом процессов теплопередачи от ПФ к горной породе окружающей обсадной колонны НС и геотермического градиента является актуальной задачей. Решению данной проблемы посвящены работы ряда авторов [1-9], которые внесли значительный вклад в решении данной проблемы. В частности академик , усовершенствовав формулы Стентона-Тейлора, получил новое выражение для определения коэффициента теплопередачи от жидкости, текущей в горизонтальной трубе к ее стенке [5]. Кроме того, он решил общее уравнение для распределения температур по длине горизонтального (транспортного) трубопровода, записанного в цилиндрических координатах. Однако, объектом исследования был горизонтальный трубопровод, а не НКТ.
Следует особенно подчеркнуть работы [1-4], посвященные определению распределения температур восходящего потока флюидов в НКТ, с учетом геотермического градиента. Однако, в указанных работах не учтено влияние теплопроводности водонефтяного слоя и газовой шапки, находящихся в пространстве между НКТ и обсадной колонной (ОК), которые на порядок ниже, чем теплопроводность углеродистой стали. Эти факторы учтены в работах [7,8], где разработан косвенный метод определения дебита НС по данным термограммы, полученной на выкидной линии скважин, но не разработана математическая модель теплопередачи от восходящего ПФ к горным породам (ГП), через несколько слоев с различными теплопроводностями.
С учетом многослойности цилиндрической стенки в работе [9] приводится следующая формула:
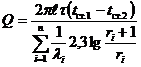 (1)
(1)
где i, n–соответственно порядковый номер и число слоев; Q – количество передаваемого тепла, ккал; ![]() - длина стенки цилиндра, м; ri - текущий радиус i-ой стенки, м; tст.1 – tст.2- разность температур внутренной и наружных поверхностей стенки, 0С;
- длина стенки цилиндра, м; ri - текущий радиус i-ой стенки, м; tст.1 – tст.2- разность температур внутренной и наружных поверхностей стенки, 0С; ![]() i- теплопроводность материала i-го слоz стенки,
i- теплопроводность материала i-го слоz стенки, 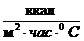 ; τ - время, часы.
; τ - время, часы.
Однако, в формуле (1) не учтены изменения Q, температуры ПФ и температуры окружающей среды (горной породы) по высоте НКТ. Кроме того, в данной формуле не учтено влияние слоя жидкости и газа в межтрубном пространстве, образованном между НКТ и обсадной колонной (ОК). Для устранения этих недостатков в данной статье предлагается комплексный подход и новая математическая модель для определения теплопередачи от восходящего потока флюидов в НКТ НС к окружающей ГП (рис.).
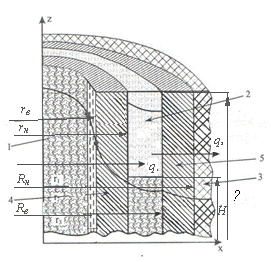
Рис. Структурная схема передачи тепла от ПФ к горной породе
1- НКТ; 2-межтрубное пространство (между НКТ и ОК); 3-ГП; 4-стенка НКТ; 5 –стенка ОК; q1,q2 – соответственно количество тепла, передаваемое за определенный период времени (секунду) через единицу поверхностей стенок НКТ и ОК; ℓ - глубина НС; Н – уровень жидкости в межтрубном пространстве; rв, rн – внутренний и внешний радиус стенки НКТ; Rв, Rн – внутренний и внешний радиус ОК.
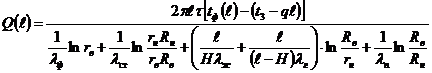 (2)
(2)
где q- геотермический градиент, oC/м; λф, λж, λг, λп, λст - теплопроводность соответственно флюида, жидкости, газа, породы и стенок НКТ и ОК.
Процесс получения формулы (2) с учетом специфических особенностей НС осуществлялся следующим образом. Сначала использован эмпирический закон Фурье в следующем виде:
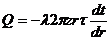
или
![]()
где z – вертикальный координат, м; t – текущая температура, оС.
Согласно структурной схемы НС интегрируя это уравнение в пределах от центра подъемной трубы (НКТ) НС до внутренней стенки, от внутренней стенки до наружной стенки, от наружной стенки НКТ до внутренней стенки ОК, от внутренней стенки до наружной стенки ОК, от наружной стенки последней в горную породу до контура питания НС получим:
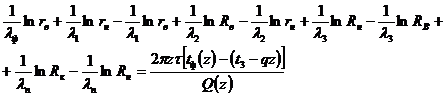 (3)
(3)
где: λ1 и λ3 – теплопроводность соответственно стенок НКТ и ОК, λ2 – теплопроводность межтрубного пространства.
Приравнивая эмпирическую формулу охлаждения Ньютона, выражающую количество тепла, переданного от стенки к жидкости и наоборот:
![]()
к формуле Фурье
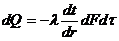
получим:
![]()
где α - коэффициент теплопередачи, ![]() ,
, ![]() и tж – соответственно температура стенки и жидкости, оС.
и tж – соответственно температура стенки и жидкости, оС.
Следовательно, вместо выражения 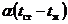 в слое жидкости и газа в межтрубном пространстве, соприкасающиеся со стенкой может быть использовано выражение
в слое жидкости и газа в межтрубном пространстве, соприкасающиеся со стенкой может быть использовано выражение ![]() .
.
Ввиду того, что значение ![]() для цилиндрической стенки НКТ и ОК одинаково, можем написать
для цилиндрической стенки НКТ и ОК одинаково, можем написать ![]() . Кроме того, жидкость и газ, заполняющие межтрубное пространство, как видно из таблицы, имеют различные значения
. Кроме того, жидкость и газ, заполняющие межтрубное пространство, как видно из таблицы, имеют различные значения ![]() .
.
Таблица
Теплопроводность газа, воды, ГП и углеристой стали
Газ | Вода | Горная порода | Углеродистая сталь | |
Теплопроводность | 0,02-0,08 | 0,51÷0,72 | 2,25 | 40 |
Причем значение ![]() воды на порядок больше, чем
воды на порядок больше, чем ![]() газа, а
газа, а ![]() углеродистой стали на два порядка больше, чем
углеродистой стали на два порядка больше, чем ![]() воды. Следовательно, межтрубное пространство, заполненное жидкостью (смесь нефти и воды) и газа является существенным барьером при передачи тепла от восходящего потока флюида в НКТ НС до горной породы, окружающей обсадную (эксплуатационную) колонну. С учетом вышеизложенного можем написать:
воды. Следовательно, межтрубное пространство, заполненное жидкостью (смесь нефти и воды) и газа является существенным барьером при передачи тепла от восходящего потока флюида в НКТ НС до горной породы, окружающей обсадную (эксплуатационную) колонну. С учетом вышеизложенного можем написать:
![]()
где Н-уровень воды в ОК, м; ℓ-глубина скважины.
Обычно, при решении задачи теплопередачи в горизонтальном трубопроводе (для перекачки жидкости) температура окружающей среды считается постоянной [5,6]. Однако, в вертикальной подъемной трубе НС это условие не соблюдается в виду с существованием геометрического градиента горной породы. Следовательно, и температура потока флюидов в подземной трубе и горной породе в зависимости от вертикальной координаты (z) будет переменными величинами. С учетом изложенного уравнение (3) приобретает следующий вид:
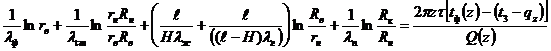 (4)
(4)
где t3 – температура ПФ в забое скважин, 0С; Rк – радиус контура питания
Наконец, с учетом вышеизложенного, из формулы (4) при значении z=ℓ получаем окончательную математическую модель процесса теплопередачи от восходящего ПФ в подъемной трубе НС к окружающей ГП.
Для определения изменения температуры восходящего потока флюидов в стволе скважин (в НКТ) в зависимости от координаты z в работах [7,8] разработана математическая модель в следующем виде:
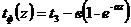 (5)
(5)
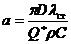 (6)
(6)
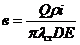 (7)
(7)
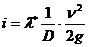 (8)
(8)
где D - диаметр НКТ, м; Q*- расход флюидов в НКТ, м3/ч; ρ – плотность ПФ, кг/м3; С- удельная теплоемкость флюидов, ккал/г, 0С; Е- механический эквивалент тепла, 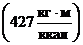 ; i - гидравлический уклон (безразмерный);
; i - гидравлический уклон (безразмерный); ![]() - коэффициент гидродинамического сопротивления (безразмерный); v – скорость потока флюидов в стволе скважин, м/сек2; g- ускорение силы тяжести, м/сек2.
- коэффициент гидродинамического сопротивления (безразмерный); v – скорость потока флюидов в стволе скважин, м/сек2; g- ускорение силы тяжести, м/сек2.
Таким образом, как видно из вышеизложенного, предложенная математическая модель (формулы (4-8)) более адекватна, т. к. учитывается геометрический градиент (ГП) и изменение температуры от забоя до выкидной линии НСк, содержание жидкости в межтрубном пространстве, образованной между НКТ и ОК и их теплопроводностей, чем существующие математические модели, описывает процесс передачи тепла от восходящего ПФ в стволе (в НКТ) НСк к окружающей ОК горной породе.
Заключение. Проведен системный анализ современного состояния процессов теплопередачи в горизонтальных трубопроводах и стволе нефтяных скважин. Показаны недостатки существующих работ при математическом моделировании процесса передачи тепла от восходящего потока флюидов к горной породе. С учетом геометрического градиента и теплопроводностей жидкости и газа, находящихся в межтрубном пространстве, т. е. между насосно-компрессорной трубой и обсадной колонной, предложена новая адекватная математическая модель процесса теплопередачи.
ЛИТЕРАТУРА
1. Чекалюк нефтяного пласта. М.: Недра, 1965.- 288с.
2. , , Штырлин аномальных данных термодинамических исследований нефтяных скважин // Нефтяное хозяйство, 2000, №3, с. 41-47
3. , , Цику состояния призабойной зоны скважины на основе комплексных исследований методами термо - и гидродинамики // Нефтяное хозяйство, 2010, №11, с. 94-97
4. Зайцев термокольматации околоскважинных зон на производительность скважин // Нефтяное хозяйство, 2011, №2, с. 83-85
5. Лейбензон трудов. Нефтепромысловая механика. Из-во Академии Наук СССР, М.: 1955, Том III, с.252-273
6. Левич -химическая гидродинамика. М.: «Физико-математическая литература», 1959.
7. Abbas Rzayev, Gambar Guluyev et al. Determining Oil Well Debit Using Оutlet Temperature Information Processing // Proceeding of the sixth International Conference on Management Science and Engineering Management. Valume 1, Chapter 4, Springer-Verlog, London, 2013, p.55-64.
8. Рзаев Аб.Г., Гулуев Г.А. и др. Связь между разностью температур на устье и дебитом в нефтяных скважинах // Известия Национальной Академии Наук Азербайджана, Баку, 2011, №3, с.125-129
9. Касаткин процессы и аппараты химической технологии. М.: «Химическая литература», 1960. -829 с.




