От умных пчёл к красивым паркетам
![]()

![]()
![]()
Прочитай текст и выполни задания 1–7.

(1) Если вы когда-нибудь видели пчелиные соты, то, возможно, замечали, что их основа – правильные шестиугольники. И это не случайно. Как доказали математики, такая конструкция очень экономична и прочна. Пчёлы же «дошли» до этого «своим умом» (рис. 1). А знаете ли вы, какие шестиугольники называют правильными?

Рис. 1 Рис. 2 Рис. 3
(2) Вам наверняка встречался треугольник, у которого равны и все стороны, и все углы. Существует и четырёхугольник с равными сторонами и равными углами – это квадрат, и пятиугольник, и шестиугольник, и т. д. (рис. 2). Многоугольник, у которого равны все стороны и все углы, называют правильным.
(3) Правильный шестиугольник составляется из правильных треугольников. Сложив три одинаковых правильных треугольника, как показано на рисунке 3, и приложив снизу ещё три таких треугольника, вы получите правильный шестиугольник. Каждая его сторона равна стороне правильного треугольника, а каждый угол – двум его углам.
(4) Интересно, что построить правильный шестиугольник можно с помощью циркуля. Для этого достаточно начертить окружность и «пройтись» по ней циркулем с шагом, равным её радиусу (рис. 4). Соединив последовательно все полученные точки, вы и получите правильный
шестиугольник. Если же соедините эти точки через одну, то получите правильный треугольник.
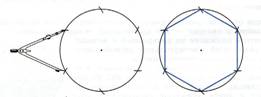
Рис. 4
(5) Вы, конечно, знаете, что такое паркет. Обычно, это дощечки прямоугольной формы, выложенные «ёлочкой» (рис. 5). Но составление паркета может быть и искусством. Им в совершенстве владели мастера, создававшие паркеты во дворцах царей и вельмож (рис. 6).
(6) В математике паркет – это покрытие плоскости фигурами без зазоров
и пересечений. Используются здесь и правильные многоугольники: на рисунке 7 изображён паркет из правильных треугольников, как бы «переходящий» в паркет из правильных шестиугольников.

Рис. 5 Рис. 6 Рис. 7
![]()
1. Прочитай название текста. Что в этом тексте связывает пчёл и паркеты?
Ответ:






2. Какой из данных пятиугольников является правильным? Обведи номер выбранного ответа.

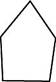

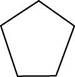
1) 2) 3) 4)
![]()
Используя прочитанный текст, объясни свой выбор. Найди в тексте и выпиши предложение, на основании которого ты сделал свой вывод.
Объяснение:




![]()
3. Рамка, которую хочет сделать Коля, имеет форму правильного шестиугольника со стороной 15 см. У Коли есть рейка длиной 1 м. Хватит ли ему этой рейки, чтобы сделать рамку? Ответ обоснуй.
Ответ: Обоснование:
4. Катя хочет сделать аппликацию в виде черепахи, изображённую на рисунке. У неё есть шаблон правильного треугольника. Сколько правильных треугольников ей надо вырезать из бумаги, чтобы сложить из них рисунок панциря черепахи? Запиши число.
Ответ:
5. Петя прочитал текст о том, как построить правильный шестиугольник с помощью циркуля. Он решил использовать этот способ для построения другого правильного многоугольника. Петя разделил окружность на шесть равных дуг, а затем точки деления соединил через одну. Какой правильный многоугольник у него получился? Обведи номер ответа.





1) | двенадцатиугольник | 3) | четырёхугольник | |
2) | шестиугольник | 4) | треугольник | |

6. На занятии математического кружка Ваня узнал, что паркеты, которые составлены только из правильных многоугольников, называют правильными паркетами. И что существует ровно 11 различных правильных паркетов. Все они показаны на этих рисунках.
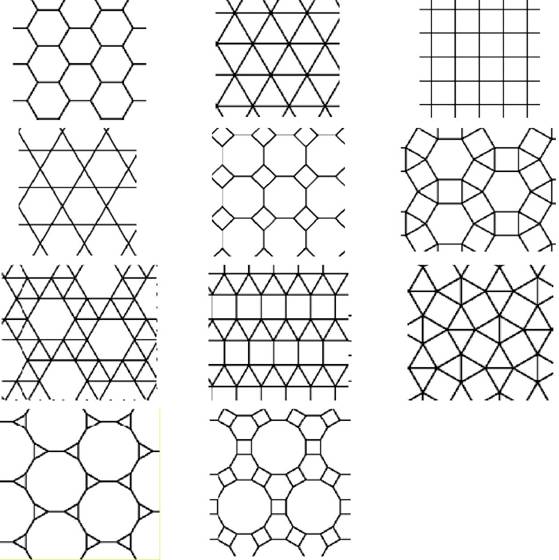
Рассматривая рисунки, Ваня сделал несколько выводов относительно правильных паркетов. Какие из них являются верными, а какие – неверными? Обведи в таблице «Да» или «Нет».
Выводы, сделанные Ваней | Верен ли вывод? | |||||
1) | Из квадратов и правильных треугольников | Да | Нет | |||
можно составить два разных паркета. | ||||||
2) | Существует только три правильных паркета, | Да | Нет | |||
которые составлены из многоугольников одного | ||||||
вида. | ||||||
3) | Каждый правильный паркет составлен из | Да | Нет | |||
многоугольников не более чем двух видов. | ||||||
4) | Из правильных пятиугольников можно составить | Да | Нет | |||
паркет. | ||||||
| ||||||
|
7. Прочитай текст из Википедии (интернет-энциклопедии):
«Сотовая связь – один из видов мобильной радиосвязи, в основе которого лежит сотовая сеть. Ключевая особенность заключается в том, что общая зона покрытия делится на ячейки (соты), определяющиеся зонами покрытия отдельных базовых станций (БС). Соты частично перекрываются и вместе образуют сеть. На идеальной (ровной и без застройки) поверхности зона покрытия одной БС представляет собой круг, поэтому составленная из них сеть имеет вид сот с шестиугольными ячейками (сотами).»
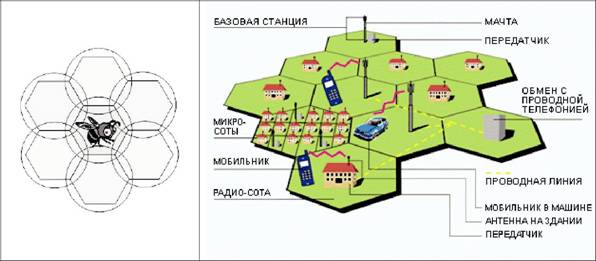
Опираясь на этот текст и рисунки, объясни, почему описанный вид мобильной связи назван сотовым.
Ответ:



 Основные порталы (построено редакторами)
Основные порталы (построено редакторами)

