 |
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
О Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №1
«Автоматизированный априорный анализ статистической совокупности в среде MS Excel»
Вариант № 9
Выполнил:
Проверил:
Уфа - 2007г.
Постановка задачи
При проведении статистического наблюдения за деятельностью предприятий корпорации получены выборочные данные по 32-м предприятиям, выпускающим однородную продукцию (выборка 10%-ная, механическая), о среднегодовой стоимости основных производственных фондов и о выпуске продукции за год.
В проводимом статистическом исследовании обследованные предприятия выступают как единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые признаки единиц.
Для проведения автоматизированного статистического анализа совокупности выборочные данные представлены в формате электронных таблиц процессора Excel в диапазоне ячеек B4:C35. Для варианта № 9 выборочные данные приведены в табл. 1-В9.
Таблица 1-В9
Исходные данные Варианта № 9
Номер предприятия | Среднегодовая стоимость основных производственных фондов, млн. руб. | Выпуск продукции, млн. руб. |
1 | 584,00 | 566,50 |
2 | 688,50 | 621,50 |
3 | 710,50 | 693,00 |
4 | 749,00 | 770,00 |
5 | 485,00 | 385,00 |
6 | 787,50 | 660,00 |
7 | 809,50 | 891,00 |
8 | 606,00 | 605,00 |
9 | 743,50 | 709,50 |
10 | 859,00 | 885,50 |
11 | 941,50 | 935,00 |
13 | 716,00 | 737,00 |
14 | 787,50 | 803,00 |
15 | 903,00 | 973,50 |
16 | 1035,00 | 1045,00 |
17 | 771,00 | 704,00 |
18 | 853,50 | 836,00 |
19 | 677,50 | 522,50 |
20 | 864,50 | 715,00 |
21 | 963,50 | 962,50 |
22 | 661,00 | 544,50 |
23 | 523,50 | 511,50 |
24 | 881,00 | 819,50 |
25 | 787,50 | 715,00 |
26 | 732,50 | 676,50 |
27 | 567,50 | 440,00 |
28 | 765,50 | 687,50 |
29 | 886,50 | 753,50 |
30 | 842,50 | 715,00 |
32 | 617,00 | 638,00 |
В процессе исследования совокупности необходимо решить ряд статистических задач для выборочной и генеральной совокупностей.
Статистический анализ выборочной совокупности
1. Выявить наличие среди исходных данных резко выделяющихся значений признаков («выбросов» данных) с целью исключения из выборки аномальных единиц наблюдения.
2. Рассчитать обобщающие статистические показатели совокупности по изучаемым признакам: среднюю арифметическую (![]() ), моду (Мо), медиану (Ме), размах вариации (R), дисперсию(
), моду (Мо), медиану (Ме), размах вариации (R), дисперсию(![]() ), средние отклонения – линейное (
), средние отклонения – линейное (![]() ) и квадратическое (σn), коэффициент вариации (Vσ), структурный коэффициент асимметрии К. Пирсона (Asп).
) и квадратическое (σn), коэффициент вариации (Vσ), структурный коэффициент асимметрии К. Пирсона (Asп).
3. На основе рассчитанных показателей в предположении, что распределения единиц по обоим признакам близки к нормальному, оценить:
а) степень колеблемости значений признаков в совокупности;
б) степень однородности совокупности по изучаемым признакам;
в) устойчивость индивидуальных значений признаков;
г) количество попаданий индивидуальных значений признаков в диапазоны (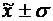 ), (
), (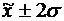 ), (
), (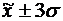 ).
).
4. Дать сравнительную характеристику распределений единиц совокупности по двум изучаемым признакам на основе анализа:
а) вариации признаков;
б) количественной однородности единиц;
в) надежности (типичности) средних значений признаков;
г) симметричности распределений в центральной части ряда.
5. Построить интервальный вариационный ряд и гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов и установить характер (тип) этого распределения. Рассчитать моду Мо полученного интервального ряда и сравнить ее с показателем Мо несгруппированного ряда данных.
Статистический анализ генеральной совокупности
1. Рассчитать генеральную дисперсию ![]() , генеральное среднее квадратическое отклонение
, генеральное среднее квадратическое отклонение ![]() и ожидаемый размах вариации признаков RN. Сопоставить значения этих показателей для генеральной и выборочной дисперсий.
и ожидаемый размах вариации признаков RN. Сопоставить значения этих показателей для генеральной и выборочной дисперсий.
2. Для изучаемых признаков рассчитать:
а) среднюю ошибку выборки;
б) предельные ошибки выборки для уровней надежности P=0,683, P=0,954, P=0,997 и границы, в которых будут находиться средние значения признака генеральной совокупности при заданных уровнях надежности.
3. Рассчитать коэффициенты асимметрии As и эксцесса Ek. На основе полученных оценок сделать вывод о степени близости распределения единиц генеральной совокупности к нормальному распределению.
СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЫБОРОЧНОЙ И ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Анализ выборочной совокупности
Задача 1. Выявим наличие среди исходных данных резко выделяющихся значений признаков («выбросов» данных) с целью исключения из выборки аномальных единиц наблюдения, используя диаграмму рассеяния. Аномальных единиц наблюдения 2 – см. Табл.2 (ПРИЛОЖЕНИЕ 1)
Задача 2. Рассчитанные обобщающие статистические показатели совокупности по изучаемым признакам: средняя арифметическая (![]() ), мода(Мо), медиана (Ме), дисперсия(
), мода(Мо), медиана (Ме), дисперсия(![]() ), средние отклонения – линейное (
), средние отклонения – линейное (![]() ) и квадратическое (σn), коэффициент вариации (Vσ), структурный коэффициент асимметрии К. Пирсона (Asп) представлены в таблицах 3 и 5 (ПРИЛОЖЕНИЕ 2). На основе этих таблиц сформируем единую Таблицу 8 значений выборочных показателей «Описательные статистики выборочной совокупности»
) и квадратическое (σn), коэффициент вариации (Vσ), структурный коэффициент асимметрии К. Пирсона (Asп) представлены в таблицах 3 и 5 (ПРИЛОЖЕНИЕ 2). На основе этих таблиц сформируем единую Таблицу 8 значений выборочных показателей «Описательные статистики выборочной совокупности»
Таблица 8
Табл. 8. Описательные статистики выборочной совокупности
По столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб." | По столбцу "Выпуск продукции, млн. руб" | ||
Среднее | 760 | Среднее | 717,3833333 |
Медиана | 768,25 | Медиана | 712,25 |
Мода | 787,5 | Мода | 715 |
Стандартное отклонение | 133,0311734 | Стандартное отклонение | 158,6947668 |
Эксцесс | -0,344943844 | Эксцесс | -0,205332365 |
Интервал | 550 | Интервал | 660 |
Дисперсия | 17107,38333 | Дисперсия | 24344,56139 |
Среднее линейное отклонение | 105,2333333 | Среднее линейное отклонение | 120,1933333 |
Коэффициент вариации,% | 17,20989423 | Коэффициент вариации,% | 21,74952089 |
Коэффициент асимметрии | -0,21025237 | Коэффициент асимметрии | 0,015275091 |
Размах вариации R равен значению интервала.
Задача 3. На основе рассчитанных показателей в предположении, что распределения единиц по обоим признакам близки к нормальному, оценим:
а) степень колеблемости значений признаков в совокупности определим по значению коэффициента вариации Vσ , исходя из оценочной шкалы:
0% < Vσ≤ 40% - колеблемость незначительная;
40% < Vσ ≤ 60% - колеблемость средняя (умеренная);
Vσ > 60% - колеблемость значительная.
Так как Vσ =17,20989423 по столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб." ; Vσ = 21,74952089 по столбцу "Выпуск продукции, млн. руб" и 0% < Vσ <(=) 40% , то колеблемость незначительная.
б) степень однородности совокупности по изучаемым признакам:
Для нормальных и близких к нормальному распределений показатель Vσ служит индикатором однородности совокупности: если Vσ ≤ 33%, то совокупность является однородной по данному признаку.
Значит, совокупность является однородной по Среднегодовой стоимости основных производственных фондов (Vσ =17,20989423) и по Выпуску продукции (Vσ = 21,74952089).
в) устойчивость индивидуальных значений признаков:
Определим отношение среднего линейного отклонения (![]() ) к квадратическому (σn); если
) к квадратическому (σn); если ![]() / σn > 0,8, то значения признака неустойчивы, в них имеются «аномальные» выбросы.
/ σn > 0,8, то значения признака неустойчивы, в них имеются «аномальные» выбросы.
1) по столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб.":
105,2333333 /133,0311734 = 0,79104266 (1)
Т. к. (1) <0,8, значит значения признака устойчивые.
2) по столбцу "Выпуск продукции, млн. руб":
120,1933333/158,6947668 =0,7573868 (2)
Т. к. (2) < 0,8, то значения признака устойчивые.
г) количество попаданий индивидуальных значений признаков в диапазоны (![]() ), (
), (![]() ), (
), (![]() ).
).
Таблица 9
Границы диапазонов | Количество значений хi, находящихся в диапазоне | |||
Первый признак | Второй признак | Первый признак | Второй признак | |
| (627;893) | (558;876) | 20 | 20 |
| (494;1026) | (399;1035) | 28 | 28 |
| (361;1159) | (240;1194) | 30 | 30 |
Табл. 9. Распределение значений признака по диапазонам рассеяния признака относительно ![]()
На основе данных таблицы 9 определим процентное соотношение рассеяния значений признака по трём диапазонам:
Всего 30 единиц наблюдения (предприятий) - 100%
20 – 66,67%
28 – 93,33%
Сопоставим полученное соотношение с ожидаемым по правилу «трёх сигм»:
Ожидаемое соотношение:
68,3% войдёт в диапазон (![]() )
)
95,4% попадёт в диапазон (![]() )
)
99,7% появится в диапазоне (![]() )
)
Полученное соотношение:
66,67% входит в диапазон (![]() )
)
93,33% попадает в диапазон (![]() )
)
100% появляется в диапазоне (![]() )
)
Задача 4. Дадим сравнительную характеристику распределений единиц совокупности по двум изучаемым признакам на основе анализа:
а) вариации признаков:
По столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб." | По столбцу "Выпуск продукции, млн. руб" | ||
Коэффициент вариации, % | 17,20989423 | Коэффициент вариации, % | 21,74952089 |
Vσ(1) первого признака (17,20989423) < Vσ(2) второго признака (21,74952089)
б) количественной однородности единиц:
Для нормальных и близких к нормальному распределений показатель Vσ служит индикатором однородности совокупности: если Vσ ≤ 33%, то совокупность является однородной по данному признаку.
Значит, совокупность является однородной по двум признакам, но она более однородна по Среднегодовой стоимости основных производственных фондов (Vσ(1) =17,20989423%), чем по Выпуску продукции (Vσ(2) = 21,74952089%).
в) надежности (типичности) средних значений признаков:
Для оценки надёжности (типичности) средней величины ![]() воспользуемся значением показателя вариации. Т. к. его значение невелико (Vσ ≤33%), то индивидуальные значения признака хi мало отличаются друг от друга, единицы наблюдения количественно однородны и, следовательно средняя величина
воспользуемся значением показателя вариации. Т. к. его значение невелико (Vσ ≤33%), то индивидуальные значения признака хi мало отличаются друг от друга, единицы наблюдения количественно однородны и, следовательно средняя величина ![]() является надёжной характеристикой данной совокупности. Для первого признака
является надёжной характеристикой данной совокупности. Для первого признака ![]() является наиболее надёжной (типичной), т. к. Vσ(1)< Vσ(2)
является наиболее надёжной (типичной), т. к. Vσ(1)< Vσ(2)
г) симметричности распределений в центральной части ряда:
В симметричном распределении характеристики центра распределения совпадают: ![]() = Мо= Ме.
= Мо= Ме.
Так как для первого признака справедливо неравенство ![]() < Ме < Мо, 760< 768,25<787,5, то для данного случая характерна левосторонняя асимметрия. Для второго признака
< Ме < Мо, 760< 768,25<787,5, то для данного случая характерна левосторонняя асимметрия. Для второго признака ![]() > Мо > Ме, 717,3833333 > 715 > 712,25- правосторонняя асимметрия.
> Мо > Ме, 717,3833333 > 715 > 712,25- правосторонняя асимметрия.
По столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб." | По столбцу "Выпуск продукции, млн. руб" | ||
Коэффициент асимметрии | -0,21025237 | Коэффициент асимметрии | 0,015275091 |
По оценочной шкале асимметричности:
|As| ≤ 0,25 – асимметрия незначительная;
0,25 < |As| ≤0,5 – асимметрия заметная (умеренная);
|As| > 0,5 – асимметрия существенная.
В данном случае асимметрия незначительная по обоим признакам, т. к.
Asп(1) = - 0,21025237 для первого признака,
Asп(2)= 0,015275091 для второго признака
и |As| ≤ 0,25
| Asп(1) | > | Asп(2) | , поэтому распределение по первому признаку более асимметрично.
Задача 5. Построим интервальный вариационный ряд и гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов и установим характер (тип) этого распределения.
Группы предприятий по среднегодовой стоимости основных фондов | Число предприятий в группе | Накопленная частость группы, % |
485-595 | 4 | 13,33% |
595-705 | 5 | 30,00% |
705-815 | 11 | 66,67% |
815-925 | 7 | 90,00% |
925-1035 | 3 | 100,00% |
Итого | 30 |
Табл. 7. Интервальный ряд распределения предприятий
по стоимости основных производственных фондов
Гистограмма
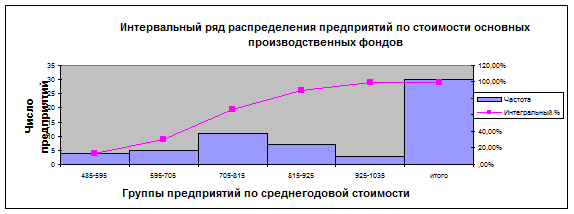
Для определения типа закономерности эмпирического распределения оно приближённо описывается теоретическим (вероятностным) распределением, форма кривой которого называется формой распределения. Расхождение между формой распределения и нормальной формой оценим показателями асимметрии и эксцесса.
Т. к. гистограмма имеет одновершинную форму, можно предполагать, что выборка является однородной по признаку Среднегодовая стоимость основных производственных фондов.
В симметричном распределении характеристики центра распределения
совпадают: ![]() = Мо= Ме;
= Мо= Ме;
As = 0, Asп = 0, R = 6 σ , где R - размах вариации
Данные соотношения нарушены, что свидетельствует о наличии асимметрии распределения. Вершина сдвинута вправо и левая часть длиннее правой, то в данном случае левосторонняя асимметрия, для которой справедливо неравенство ![]() < Ме < Мо, 760< 768,25< 787,5; оно означает что в распределении чаще встречаются более низкие значения признака. Распределение с незначительной асимметрией (задача 4 п. г ) часто относят к нормальному.
< Ме < Мо, 760< 768,25< 787,5; оно означает что в распределении чаще встречаются более низкие значения признака. Распределение с незначительной асимметрией (задача 4 п. г ) часто относят к нормальному.
Показатель эксцесса характеризует крутизну кривой распределения - её заострённость или пологость по сравнению с нормальной кривой.
Коэффициент эксцесса Еk = - 0,344943844, Еk < 0, это значит, что значения данного признака достаточно равномерно рассеяны по всему диапазону от xmax до xmin.
Т. о. гистограмма приблизительно симметрична, её «хвосты» не очень длинны, поэтому она представляет распределение, близкое к нормальному.
Рассчитаем моду Мо* полученного интервального ряда по формуле:
Mo* = XMo + h*[ (fMo – fMo-1) / (fM – fMo-1) + (fMo + fMo-1)],
где XMo – нижняя граница модального интервала,
h – величина модального интервала,
fMo – частота модального интервала
Mo* = 705 + 110 * [(11-5) / (11-5) + (11-7)] = 771
Сравним ее с показателем Мо несгруппированного ряда данных:
Mo = 787,5 ( из табл. 3 ПРИЛОЖЕНИЕ 2) Mo* =771; Mo* < Mo
Анализ генеральной совокупности
Задача 1. Значения генеральной дисперсии ![]() , генерального среднего квадратического отклонения
, генерального среднего квадратического отклонения ![]() , коэффициент асимметрии К. Пирсона (Asп), эксцесс Еk приведены в таблице 3. Сформируем для них таблицу 10 «Описательные статистики генеральной совокупности».
, коэффициент асимметрии К. Пирсона (Asп), эксцесс Еk приведены в таблице 3. Сформируем для них таблицу 10 «Описательные статистики генеральной совокупности».
Таблица 10
По столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб." | По столбцу "Выпуск продукции, млн. руб" | ||
Стандартное отклонение | 133,0311734 | Стандартное отклонение | 158,6947668 |
Дисперсия выборки | 17697,2931 | Дисперсия выборки | 25184,02902 |
Эксцесс | -0,344943844 | Эксцесс | -0,205332365 |
Асимметричность | -0,152503649 | Асимметричность | 0,042954448 |
Табл. 10. Описательные статистики генеральной совокупности
Установим степень расхождения между ![]() и
и ![]() по формуле:
по формуле:
![]() = n/(n-1)*
= n/(n-1)*![]()
1)для первого признака: ![]() = 30 / (30 - 1) * 17107,38333=17697,2931,
= 30 / (30 - 1) * 17107,38333=17697,2931,
![]() и
и ![]() совпадают
совпадают
2)для второго признака:![]() = 30 / (30 - 1) * 24344,56139=25184,02902,
= 30 / (30 - 1) * 24344,56139=25184,02902,
![]() и
и ![]() отличаются незначительно.
отличаются незначительно.
Прогнозные оценки размаха вариации RN рассчитаем по формуле:
R = 6 σ и сравним для каждого признака прогнозное значение RN с Rn.
1)для первого признака: RN = 6 *133,0311734 = 798,1870404
Rn = 550, RN > Rn
2)для второго признака: RN = 6 *158,6947668 = 952,1686008
Rn = 660, RN > Rn
Задача 2. Для изучаемых признаков рассчитаем:
а) Средние ошибки выборки рассчитаны и приведены в таблице 3.
По столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб." | По столбцу "Выпуск продукции, млн. руб" | ||
Стандартная ошибка | 24,28805818 | Стандартная ошибка | 28,97356785 |
б) Оценки предельных ошибок выборки для уровней надежности P=0,683, P=0,954, P=0,997 имеются в табл. 3, табл. 4а, табл. 4б.
Найдём границы, в которых будут находиться средние значения признака генеральной совокупности при заданных уровнях надежности Х = ![]() ± ∆х.
± ∆х.
Таблица 11
Доверительная вероятность Р | Коэффициент доверия t | Предельные ошибки выборки | Ожидаемые границы для средних х | ||
Для первого признака | Для второго признака | Для первого признака | Для второго признака | ||
0,683 | 1 | 24,73023361 | 29,50104517 | 735,2697664 ≤Х≤ 784,7302336 | 687,8822881 ≤Х≤ 746,8843785 |
0,954 | 2 | 50,63603436 | 60,404441 | 709,3639656 ≤Х≤ 810,6360344 | 656,9788923 ≤Х≤ 777,7877743 |
0,997 | 3 | 78,67878057 | 93,85702927 | 681,3212194 ≤Х≤ 838,6787806 | 623,526304 ≤Х≤ 811,2403626 |
Табл. 11. Предельные ошибки выборки и ожидаемые границы для генеральных средних
Задача 3. Значения коэффициентов асимметрии As и эксцесса Ek приведены в таблице 10.
По столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб." | По столбцу "Выпуск продукции, млн. руб" | ||
Эксцесс | -0,344943844 | Эксцесс | -0,205332365 |
Асимметричность | -0,152503649 | Асимметричность | 0,042954448 |
Так как распределение единиц выборочной совокупности близко к нормальному, выборка является репрезентативной (значения показателей ![]() и
и ![]() расходятся незначительно) и при этом коэффициенты
расходятся незначительно) и при этом коэффициенты
AsN (1) = - 0,152503649, AsN (2) = 0,042954448 указывают на небольшую величину асимметрии; EkN(1) = - 0,344943844, EkN(2) = - 0,205332365 указывают на умеренную величину эксцесса. На основе этого можно считать, что распределение единиц генеральной совокупности по изучаемым признакам будет близко к нормальному.
ПРИЛОЖЕНИЕ 1
Исходные данные | ||
Номер предприятия | Среднегодовая стоимость основных производственных фондов, млн. руб. | Выпуск продукции, млн. руб. |
1 | 584,00 | 566,50 |
2 | 688,50 | 621,50 |
3 | 710,50 | 693,00 |
4 | 749,00 | 770,00 |
5 | 485,00 | 385,00 |
6 | 787,50 | 660,00 |
7 | 809,50 | 891,00 |
8 | 606,00 | 605,00 |
9 | 743,50 | 709,50 |
10 | 859,00 | 885,50 |
11 | 941,50 | 935,00 |
13 | 716,00 | 737,00 |
14 | 787,50 | 803,00 |
15 | 903,00 | 973,50 |
16 | 1035,00 | 1045,00 |
17 | 771,00 | 704,00 |
18 | 853,50 | 836,00 |
19 | 677,50 | 522,50 |
20 | 864,50 | 715,00 |
21 | 963,50 | 962,50 |
22 | 661,00 | 544,50 |
23 | 523,50 | 511,50 |
24 | 881,00 | 819,50 |
25 | 787,50 | 715,00 |
26 | 732,50 | 676,50 |
27 | 567,50 | 440,00 |
28 | 765,50 | 687,50 |
29 | 886,50 | 753,50 |
30 | 842,50 | 715,00 |
32 | 617,00 | 638,00 |
ПРИЛОЖЕНИЕ 2
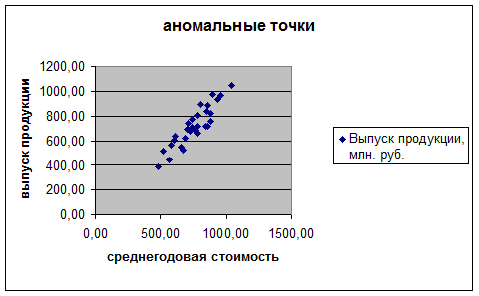
Таблица 2 | ||
Аномальные единицы наблюдения | ||
Номер предприятия | Среднегодовая стоимость основных производственных фондов, млн. руб. | Выпуск продукции, млн. руб. |
12 | 320,00 | 825,00 |
31 | 1035,00 | 275,00 |
ПРИЛОЖЕНИЕ 3
Таблица 3 | |||
Описательные статистики | |||
По столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб." | По столбцу "Выпуск продукции, млн. руб" | ||
Столбец1 | Столбец2 | ||
Среднее | 760 | Среднее | 717,3833333 |
Стандартная ошибка | 24,28805818 | Стандартная ошибка | 28,97356785 |
Медиана | 768,25 | Медиана | 712,25 |
Мода | 787,5 | Мода | 715 |
Стандартное отклонение | 133,0311734 | Стандартное отклонение | 158,6947668 |
Дисперсия выборки | 17697,2931 | Дисперсия выборки | 25184,02902 |
Эксцесс | -0,344943844 | Эксцесс | -0,205332365 |
Асимметричность | -0,152503649 | Асимметричность | 0,042954448 |
Интервал | 550 | Интервал | 660 |
Минимум | 485 | Минимум | 385 |
Максимум | 1035 | Максимум | 1045 |
Сумма | 22800 | Сумма | 21521,5 |
Счет | 30 | Счет | 30 |
Уровень надежности(95,4%) | 50,63603436 | Уровень надежности(95,4%) | 60,404441 |
Таблица 4а | |||
Предельные ошибки выборки | |||
По столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб." | По столбцу "Выпуск продукции, млн. руб" | ||
Столбец1 | Столбец2 | ||
Уровень надежности(68,3%) | 24,73023361 | Уровень надежности(68,3%) | 29,50104517 |
Таблица 4б | |||
Предельные ошибки выборки | |||
По столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб." | По столбцу "Выпуск продукции, млн. руб" | ||
Столбец1 | Столбец2 | ||
Уровень надежности(99,7%) | 78,67878057 | Уровень надежности(99,7%) | 93,85702927 |
Таблица 5 | |||
Выборочные показатели вариации и асимметрии | |||
По столбцу "Среднегодовая стоимость основных производственных фондов, млн. руб." | По столбцу "Выпуск продукции, млн. руб" | ||
Стандартное отклонение | 130,7951961 | Стандартное отклонение | 156,0274379 |
Дисперсия | 17107,38333 | Дисперсия | 24344,56139 |
Среднее линейное отклонение | 105,2333333 | Среднее линейное отклонение | 120,1933333 |
Коэффициент вариации, % | 17,20989423 | Коэффициент вариации, % | 21,74952089 |
Коэффициент асимметрии | -0,21025237 | Коэффициент асимметрии | 0,015275091 |




