Компьютерный практикум «Решение задач линейного программирования с использованием Microsoft Excel»

Компьютерный практикум «Решение задач линейного программирования с использованием Microsoft Excel»

ЦЕЛЬ РАБОТЫ

Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Для задачи ЛП составьте модель задачи и найдите оптимальное решение в табличном редакторе Microsoft Excel.

2. Оформите отчет по лабораторной работе, который должен содержать:

§  исходные данные задачи;

§  модель задачи;

§  последовательность действий для решения задачи в табличном редакторе Microsoft Excel;

Пример решения задачи.

Фирма производит два вида продукции: А и В. Прибыль на единицу продукции А и В составляет соответственно 360 и 240 евро.

Технология производства требует работы 3 машин. Время работы машин 1, 2, 3 в минутах, необходимое для производства единицы продукции каждого вида, приведено в таблице.

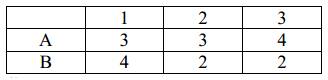
Еженедельный резерв времени работы машин равен соответственно 36, 32 и 40 часов в день. Определите ежедневные нормы выпуска продукции 1 и 2, максимизирующие прибыль.

Решение.

Построим математическую модель. Введем обозначения x1 и x2 для количества изделий моделей А и В.

Прибыль от реализации данной продукции равна L=360x1 + 240x2→max

Эту прибыль нужно максимизировать. Это целевая функция (для нее ищется экстремум (минимум или максимум).

Бесконечному росту целевой функции препятствуют ограничения, т. к. они не дают возможности бесконечно увеличивать количество производимой продукции А и В. Мы имеем ограничения лишь по времени работы машин.

Переведем время, необходимое для производства единицы продукции каждого вида, данное в минутах, в часы. Получим: по продукции А – 0,05, 0,05, 0,06; по продукции
В – 0,06, 0,03, 0,03. Ограничение по резерву времени для машины 1 выглядит следующим образом: 0,05x1 + 0,06x2 ≤ 36,

Для машины 2: 0,05x1 + 0,03x2 ≤ 32, для машины 3: 0,06x1 + 0,03x2 ≤ 40.

Последнее ограничение – количества изделий не могут быть отрицательными числами, поэтому x1 ≥ 0, x2≥0.

Модель задачи:

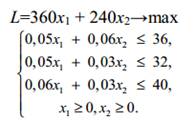
В настоящее время одним из наиболее известных способов численного решения задач линейного программирования является использование надстройки «Поиск решения» электронных таблиц Microsoft Excel.

Теоретической основой надстройки «Поиск решения» является симплекс-метод, позволяющий находить оптимальное решение задачи планирования с помощью итерационного процесса перехода к улучшающимся планам. «Поиск решения» является дополнением Excel, т. е. может не входить в стандартный вариант установки электронных таблиц.

Для его добавления достаточно воспользоваться командой Данные - Поиск решения.

При решении задачи с помощью надстройки Поиск решения необходимо:

1) открыть окно Microsoft Excel;

2) заполнить ячейки A1-А3 таблицы обозначениями x1 , x2 и max соответственно (см. рис. 1);

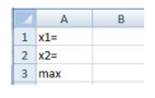
Рис. 1

3) в ячейку В3 записать формулу L=360x1 + 240x2 через адреса соответствующих ячеек =360*B1+240*B2 (адреса ячеек вводятся щелчком мыши по соответствующей ячейке или набираются с клавиатуры на английской раскладке), нажать Enter.

4) в диапазон ячеек А7-С9 записать систему ограничений через адреса соответствующих ячеек, т. е. в А7 ввести формулу =0,05*B1+0,06*B2, нажать Enter, в А8 ввести формулу =0,05*B1+0,03*B2, нажать Enter, в А9 ввести формулу =0,06*B1+0,03*B2, нажать Enter, в ячейки В7-В9 ввести слова не более, в ячейки С7-С9 36, 32 и 40 соответственно (см. рис. 2);

Рис. 2

5) для решения поставленной задачи в вкладке Данные выбрать пункт Поиск

решения (см. рис. 3);

Рис. 3

6) в появившемся окне Поиск решения в поле Установить целевую ячейку надо щёлкнуть по кнопке , затем в ячейке B3 и снова по кнопке ; в поле Равной установить флажок (щёлкнуть левой кнопкой мыши в соответствующем кружке) максимальному значению, в поле Изменяя ячейки щёлкнуть по кнопке , выделить мышью диапазон ячеек В1 - В2 и снова щёлкнуть по кнопке (см. рис. 4);

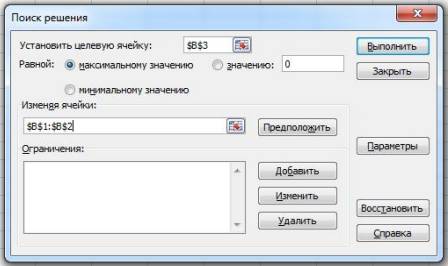
Рис. 4

7) в этом же окне Поиск решения осталось незаполненным поле Ограничения, поэтому надо нажать на кнопку Добавить: появится новое окно Добавление ограничения, в поле Ссылка на ячейку надо щёлкнуть по кнопке , затем выделить мышью диапазон ячеек В1-В2 и снова щёлкнуть по кнопке , в следующем поле необходимо выбрать знак >=, нажав , затем в поле Ограничение ввести 0 (см. рис. 5);

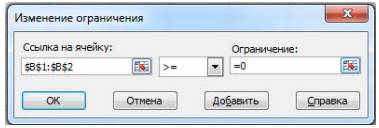
Рис. 5

8) в этом же окне Добавление ограничения нажать кнопку Добавить (появится новое лось окно Добавление ограничения) и ввести новое ограничение: в поле Ссылка на ячейку надо щёлкнуть по кнопке , затем выделить мышью диапазон ячеек А7-А9 и снова щёлкнуть по кнопке , в следующем поле необходимо выбрать знак <=, нажав , затем в поле Ограничение надо щёлкнуть по кнопке , затем выделить мышью диапазон ячеек C7-C9 и снова щёлкнуть по кнопке (см. рис. 6);

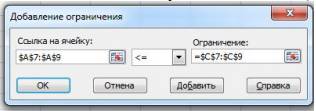
Рис. 6

9) теперь все ограничения нами учтены: надо нажать кнопку ОК, после чего снова откроется диалоговое окно Поиск решения, и надо нажать кнопку Параметры;

10) в диалоговом окне параметры поиска решения необходимо установить галочки напротив опций Линейная модель и Неотрицательные значения (рис. 7);

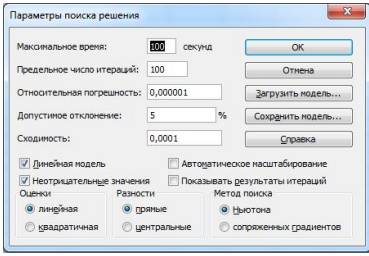
Рис. 7

11) щелкните кнопку ОК. Вы окажетесь в исходном окне. Теперь все готово для работы алгоритма поиска решения. Нажмем кнопку Выполнить. (рис.8);

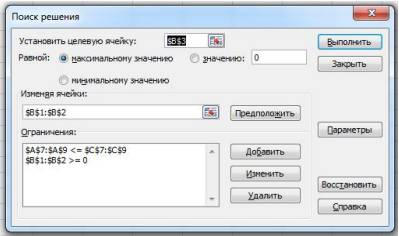
Рис. 8

12) в появившемся диалоговом окне Результаты поиска решения (в котором компьютер предлагает по умолчанию сохранить найденное решение) надо нажать кнопку ОК (рис. 9).

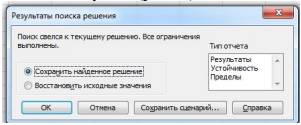
Рис. 9

13) Результат полученных вычислений представлен на рис. 10.

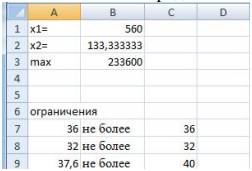
Рис. 10

Мы видим что вид таблицы изменился. В ячейках В1 и В2 появились значения 560 и 133,33 изделий А и В соответственно. При этом целевая функция достигает максимального значения 233 600. Кроме того в ячейках А7, А8, А9 появились значения 36, 32, 37,6, означающие максимально полное использование ресурсов времени работы машин.

Замечание 1. Если часть ограничений представляют собой неравенства другого знака, то все коэффициенты и свободные члены для данных строк умножаются на -1 и знак выставляется одинаковый для всей системы.

Замечание 2. На практике часто требуется, чтобы на переменные налагалось условие целочисленности (например, если какой-то продукт нельзя разрезать на части, а можно добавлять в рацион только целыми порциями), в этом случае в окне Добавление ограничения, в поле Ссылка на ячейку надо щёлкнуть по кнопке , затем выделить мышью диапазон ячеек и снова щёлкнуть по кнопке , в следующем поле необходимо выбрать условие ЦЕЛ, нажав (рис. 11).

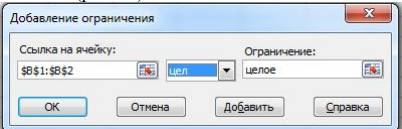
Рис. 11

Задания для самостоятельной работы

Решить задачу в Microsoft Excel

Задача 1.

Для осуществления перевозок по трем городским маршрутам используются автобусы двух типов. Автобусы первого типа вмещают 100 пассажиров, второго типа – 120 пассажиров. Количество автобусов на маршруте, необходимость в перевозке пассажиров, эксплуатационные расходы каждого вида автобусов даны в таблице.

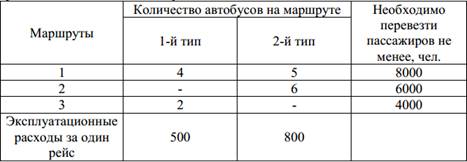
Определить, какое количество рейсов должно быть выполнено автобусами на каждом маршруте, чтобы расходы от перевозок были минимальными.

Задача 2.

Фабрика выпускает два вида каш для завтрака. Используемые для производства обоих продуктов ингредиенты в основном одинаковы и, как правило, не являются дефицитом. Основным ограничением, накладываемым на объем выпуска, является наличие фонда рабочего времени в каждом из трех цехов фабрики. В приведенной ниже таблице указаны общий фонд рабочего времени и число человеко-часов, требуемое для производства 1 т продукта. Доход от производства 1 т первого тип каши составляет 3750 евро, а от производства второго типа каши – 1875 евро. На настоящий момент нет никаких ограничений на возможные объемы продаж.

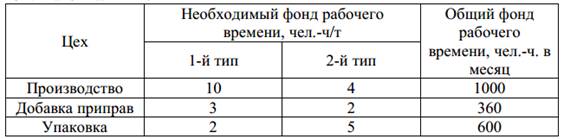
Требуется спланировать работу фабрики так, чтобы общий доход за месяц был максимальным.

Задача 3.

Небольшая фабрика изготавливает два вида красок: для внутренних (I) и наружных (II) работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта A и B. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 т, соответственно. На одну тонну краски I расходуется 2 т продукта A и 1 т продукта B. На одну тонну краски II расходуется 1 т продукта A и 2 т продукта B. Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску II более чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки. Оптовые цены одной тонны краски равны: 2 тыс. долл. для краски I и 3 тыс. долл. для краски II. Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

Задача 4.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 часами в сутки. Время обработки и прибыль от продажи одного изделия каждого вида приведены в таблице.

Требуется найти оптимальные объемы производства изделий каждого вида.