Коэффициент Джини, коэффициент Лоренца

ОГЛАВЛЕНИЕ

Введение. 3

Дифференциация доходов населения. 4

Кривая Лоренца (коэффициент Лоренца) 5

Коэффициент Джини. 9

Заключение. 14

Список литературы.. 15

ВВЕДЕНИЕ

С переходом к рыночной экономике резко обострился процесс расслоения общества по уровню доходов, и это обусловило необходимость внедрения в статистическую практику показателей для анализа социально-экономической дифференциации населения. К этим показателям относятся:

Модальный доход;

Медианный доход;

Децильный коэффициент дифференциации доходов населения;

Коэффициенты концентрации Лоренца и Джини.

Цель данной работы – изучить такие показатели социально-экономической дифференциации населения как коэффициент Лоренца и Джини.

ДИФФЕРЕНЦИАЦИЯ ДОХОДОВ НАСЕЛЕНИЯ

Дифференциация доходов населения - это объективно складывающиеся различия в уровне доходов индивидов и социальных групп, обусловленные различиями в оплате труда и социальных выплат, способностях и предприимчивости, имущественном положении [3].

Денежные доходы населения включают в себя заработную плату, социальные трансферты, предпринимательские доходы, проценты, дивиденды и другие доходы от собственности, а также общую стоимость продукции - личного подсобного хозяйства, потребленной в семье и проданной. Доходы населения распределяются по группам населения неравномерно [5].

Существует ряд показателей оценки дифференциации доходов населения, которые позволяют увидеть, насколько интенсивно протекает данный процесс. В их числе:

ü  распределение населения по уровню среднедушевых доходов (модальный и медианный доходы) - это показатель удельного веса или процента населения в тех или иных заданных интервалах среднедушевых денежных доходов.

ü  распределение общего объема денежных доходов по различным группам населения - показатель в процентах доли общего объема денежных доходов, которой обладает каждая из групп населения - кривая фактического распределения дохода (кривая Лоренца)

ü  коэффициент концентрации доходов (индекс Джини)

ü  децильный коэффициент дифференциации доходов – соотношение среднедушевых денежных доходов последней и первой групп населения. Он показывает, во сколько раз доходы n% наиболее обеспеченного населения превышают доходы n% наименее обеспеченного населения [4].

Далее рассмотрим более подробно кривую Лоренца (коэффициент Лоренса) и индекс Джини (коэффициент Джини).

КРИВАЯ ЛОРЕНЦА (КОЭФФИЦИЕНТ ЛОРЕНЦА)

Кривая Лоренца – это графическое изображение концентрации отдельных элементов совокупности по группам: концентрация населения по группам семей с разным уровнем душевого дохода; концентрация работающих по группам с разным уровнем оплаты труда [1].

Кривая Лоренца отражает кумулятивные (накопленные) доли дохода населения. Кривая Лоренца — это графическое изображение функции распределения. Она была предложена американским экономистом Максом Отто Лоренцем в 1905 году как показатель неравенства в доходах населения. В таком представлении она есть изображение функции распределения, в котором аккумулируются доли численности и доходов населения. В прямоугольной системе координат кривая Лоренца является выпуклой вниз и проходит под диагональю единичного квадрата, расположенного в I координатной четверти [6].

Каждая точка на кривой Лоренца соответствует утверждению вроде «20 самых бедных процентов населения получают всего 7% дохода». В случае равного распределения каждая группа населения имеет доход, пропорциональный своей численности. Такой случай описывается кривой равенства (line of perfect equality), являющейся прямой, соединяющей начало координат и точку (1;1). В случае полного неравенства (когда лишь один член общества имеет доход) кривая (line of perfect inequality) сначала «прилипает» к оси абсцисс, а потом из точки (1;0) «взмывает» к точке (1;1).

Если распределение равномерное, попарные доли осей абсцисс и ординат должны совпадать (ось абсцисс – 0, 20, 40, 60, 80, 100, ось ординат соответственно – 2, 20, 40, 60, 80, 100) и располагается по диагонали квадрата, что означает полное отсутствие концентрации объема признака.

При абсолютном неравенстве при оси ординат должно быть 0, 0, 0, 0, 0, 100. Это означает, например, в случае концентрации доходов семей: все население за исключением одной семьи, не имеет доходов, а это одна семья получает весь доход. Абсолютное неравенство — тот гипотетический случай, когда все население, за исключением одного человека (одной семьи), не имеет доходов, а этот один (одна семья) получает весь доход. Это практически гипотетический случай, который вряд ли можно ожидать [1].

Кривая Лоренца заключена между кривыми равенства и неравенства. Очевидно, в конкретных случаях нельзя ожидать ни абсолютного равенства, ни абсолютного неравенства в распределении доходов среди населения.

Кривые Лоренца применяют для распределений не только доходов, но и имущества домохозяйств, долей рынка для фирм в отрасли, природных ресурсов по государствам. Встретить кривую Лоренца можно и за пределами экономической науки [8].

Рассмотрим кривую Лоренца на примере ее построения. Построение кривой Лоренца удобнее всего рассмотреть на следующем примере: 

Представим экономику, состоящую из 3-х агентов: А, B, C. Доход агента А составляет 200 единиц, доход агента В составляет 300 единиц, доход агента С составляет 500 единиц. 

Для построения кривой Лоренца найдем доли индивидов в общем доходе. Общий доход составляет 1000. Тогда доля индивида А составляет 20%, доля В составляет 30%, доля С составляет 50%. 

Далее будем искать кумулятивные (накопленные) доли доходов и численности населения для индивидов, начав с самого бедного и постепенно включая более богатых индивидов: 

Доля в населении индивида А составляет 33%. Доля его дохода составляет 20%. Затем включим в анализ более богатого индивида – индивида В. Совместная доля А+В в населении составляет 67%. Совместная доля А+В в доходе составляет 50% (20%+30%). Далее включим в анализ еще более богатого индивида С. Совместная доля А+В+С в населении составляет 100%. Совместная доля А+В+С в доходе составляет 100% (20%+30%+50%) [10]. 

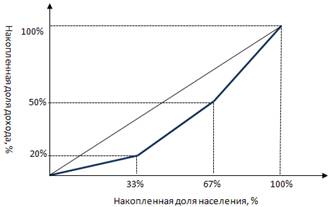Отметим полученные результаты на графике:

Линия, соединяющая левую нижнюю точку и правую верхнюю точку графика, называется линией равномерного распределения доходов. Это гипотетическая линия, которая показывает, что было бы, если доходы в экономике распределяются равномерно. При неравномерном распределении доходов кривая Лоренца лежит левее этой линии, причем чем больше степень неравенства, тем сильнее изгиб кривой Лоренца. А чем ниже степень неравенства, тем более она приближена к линии абсолютного равенства [9]. 

В нашем случае кривая Лоренца выглядит как кусочно-линейный график. Это получилось так, потому что в нашем анализе мы выделили только три группы населения. С ростом числа рассматриваемых групп населения 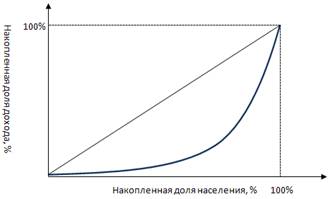кривая Лоренца будет выглядеть следующим образом: 

Кривая Лоренца позволяет судить о степени неравенства доходов в экономике о ее изгибу.

Относительная характеристика неравенства в распределении доходов определяются при помощи коэффициента концентрации Лоренца и Джини.

Коэффициент Лоренца как относительная характеристика неравенства в распределении доходов. Коэффициент Лоренца - это доля площади отклонения от равномерного распределения диагонали квадрата в половине площади этого квадрата либо это отношение фактической суммы абсолютных разностей долей в объеме совокупности и в объеме признака по группам максимально возможному значению этой суммы.

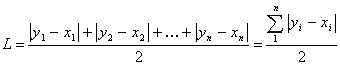где уi — доля доходов, сосредоточенная у i-й социальной группы населения; хi — доля населения, принадлежащая к i-й социальной группе в общей численности населения; n — число социальных групп [1].

Экстремальные значения коэффициента Лоренца: L = 0 в случае полного равенства в распределении доходов; L = 1 — при полном неравенстве. Для количественного измерения степени неравенства дохода по кривой Лоренца существует специальный коэффициент – коэффициент Джини. 

КОЭФФИЦИЕНТ ДЖИНИ

Коэффициент Джини, как и коэффициент Лоренца, используется для характеристики концентрации доходов. Коэффициент Джини — статистический показатель степени расслоения общества данной страны или региона по отношению к какому-либо изучаемому признаку. Наиболее часто в современных экономических расчётах в качестве изучаемого признака берётся уровень годового дохода [7].

Коэффициент Джини можно определить, как макроэкономический показатель, характеризующий дифференциацию денежных доходов населения в виде степени отклонения фактического распределения доходов от абсолютно равного их распределения между жителями страны.

Иногда используется процентное представление этого коэффициента, называемое индексом Джини.

Иногда коэффициент Джини (как и кривую Лоренца) используют также и для выявления уровня неравенства по накопленному богатству, однако в таком случае необходимым условием становится неотрицательность чистых активов домохозяйства [6].

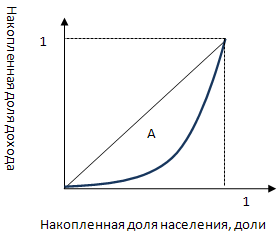
Коэффициент Джини равен отношению площади фигуры, ограниченной прямой абсолютного равенства и кривой Лоренца, к площади всего треугольника под кривой Лоренца. 
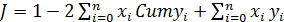, где уi — доля доходов, сосредоточенная у i-й социальной группы населения; Cumyi – кумулятивная доля доходов, хi — доля населения, принадлежащая к i-й социальной группе в общей численности населения; n — число социальных групп [1].

Если кривая Лоренца изображена не в %, а в долях, то площадь большого треугольника всегда равна ½. Формула коэффициента Джини для этого случая приобретает вид: J = 2*SA. Коэффициент Джини может принимать значения от 0 до 1. Чем ближе коэффициент Джини к нулю, тем меньше изгиб кривой Лоренца, и доходы распределены более равномерно. Чем ближе коэффициент Джини к единице, тем больше изгиб кривой Лоренца, и доходы распределены менее равномерно. 

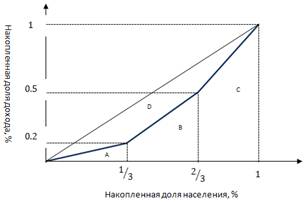Рассчитаем коэффициент Джини для нашего примера с тремя индивидами. Для этого построим кривую Лоренца в долях, а не в %

 Площадь внутренней фигуры D быстрее всего можно посчитать путем вычитания из площади большого треугольника площади фигур А, В и С [10].

 
В этом случае коэффициент Джини будет равен: 

Как известно, любой статистический показатель имеет плюсы и минусы. Преимущества коэффициента Джини, следующие:

Позволяет сравнивать распределение признака в совокупностях с различным числом единиц (например, регионы с разной численностью населения) [7].

Дополняет данные о ВВП и среднедушевом доходе. Служит своеобразной поправкой этих показателей.

Может быть использован для сравнения распределения признака (дохода) между различными совокупностями (например, разными странами). При этом нет зависимости от масштаба экономики сравниваемых стран.

Может быть использован для сравнения распределения признака (дохода) по разным группам населения (например, коэффициент Джини для сельского населения и коэффициент Джини для городского населения).

Позволяет отслеживать динамику неравномерности распределения признака (дохода) в совокупности на разных этапах.

Анонимность — одно из главных преимуществ коэффициента Джини. Нет необходимости знать, кто имеет какие доходы персонально [6].

Помимо плюсов, любой статистический показатель имеет свои изъяны. Так же, как и по показателю ВВП нельзя судить об уровне благосостояния экономики, и коэффициент Джини (и другие показатели степени неравенства) не могут дать в полной мере объективную картину степени неравенства доходов в экономике. 

Это происходит по нескольким причинам:

Во-первых, уровень дохода индивидов не является постоянным и может резко изменяться с течением времени. Доходы молодых людей, которые только что закончили университет, как правило, являются минимальными, и затем начинают расти по мере того, как человек набирается опыта и наращивает человеческий капитал. Доходы людей, как правило, достигают пика между 40 и 50 годами, и затем резко снижаются, когда человек уходит на пенсию. Э то явление называется в экономике жизненным циклом. 

Но человек имеет возможность компенсировать различие в доходах на разных этапах жизненного цикла с помощью финансового рынка – беря кредиты или делая сбережения. Так, молодые люди, находящиеся в самом начале жизненного цикла, охотно берут кредиты на образование или ипотечные кредиты. Люди, которые находятся ближе к окончанию экономического жизненного цикла, активно делают сбережения. 

Кривая Лоренца и коэффициент Джини не учитывают жизненный цикл, поэтому этот показатель степени неравенства доходов в обществе не является точной оценкой степени неравенства доходов. 

Во-вторых, на доходы индивидов влияет экономическая мобильность. В частности, экономика США является примером экономики возможностей, когда индивид из низов может благодаря сочетанию усердия, таланта и удачи, стать очень успешным человеком, и история знает множество подобных примеров. Но также известны случаи потери крупных состояний или даже полных банкротств вполне состоятельных предпринимателей. Как правило, в таких экономиках, как экономика США, отдельное домохозяйство за свою жизнь успевает побывать в нескольких категориях распределения доходов. И связано это с высокой экономической мобильностью. Так, например, какое-то домохозяйство может в одном году входит в группу с самым низким уровнем дохода, а следующем году уже в группу со средним уровнем доходов. Кривая Лоренца и коэффициент Джини также не учитывают данный эффект. 

В-третьих, индивиды могут получать трансферты в натуральной форме, которые не отражаются в кривой Лоренца, хотя при этом влияют на распределение доходов индивидов. Трансферты в натуральной форме могут быть реализованы в виде помощи беднейшим слоям населения продуктами питания, одеждой, но обычно они предоставляются в виде многочисленных льгот (бесплатный проезд в общественном транспорте, бесплатные путевки в санатории и так далее). С учетом подобных трансфертов экономическое положение беднейших слоев населения улучшается, но кривая Лоренца и коэффициент Джини этого не учитывают. Не так давно в России многие льготы были монетизированы, и объективные доходы беднейших слоев населения стало считать легче. Следовательно, кривая Лоренца стала лучше отражать реальное распределение доходов в обществе [11].

Таким образом, кривая Лоренца и коэффициент Джини используются для оценки степени неравенства доходов, и входят в область позитивного экономического анализа. Напомним, что позитивный анализ отличается от нормативного анализа тем, что позитивный анализ анализирует экономику объективно, как есть, а нормативный анализ является попыткой улучшить мир, сделать «как должно быть». Если оценка степени неравенства является позитивным экономическим анализом, то попытки снизить неравенство в распределении доходов принадлежат к области нормативного экономического анализа. 

Нормативный экономический анализ известен тем, что разные экономисты могут предложить разное, часто диаметральное противоположные рекомендации по решению одной и той же проблемы. Это не означает, что кто-то является более компетентным, а кто менее компетентным. Это только означает, что экономисты отталкиваются от различных философских взглядов на понятие справедливости, а единства в этом вопросе нет [2]. 

ЗАКЛЮЧЕНИЕ

Дифференциация доходов населения - это объективно складывающиеся различия в уровне доходов индивидов и социальных групп, обусловленные различиями в оплате труда и социальных выплат, способностях и предприимчивости, имущественном положении.

Существует ряд показателей оценки дифференциации доходов населения, в частности коэффициенты Лоренца и Джини.

Кривая Лоренца – это графическое изображение концентрации отдельных элементов совокупности по группам: концентрация населения по группам семей с разным уровнем душевого дохода; концентрация работающих по группам с разным уровнем оплаты труда.

Коэффициент Лоренца как относительная характеристика неравенства в распределении доходов. Коэффициент Лоренца - это доля площади отклонения от равномерного распределения диагонали квадрата в половине площади этого квадрата либо это отношение фактической суммы.

Коэффициент Джини — статистический показатель степени расслоения общества данной страны или региона по отношению к какому-либо изучаемому признаку.

Коэффициент Джини равен отношению площади фигуры, ограниченной прямой абсолютного равенства и кривой Лоренца, к площади всего треугольника под кривой Лоренца.

Таким образом, кривая Лоренца и коэффициент Джини используются для оценки степени неравенства доходов, и входят в область позитивного экономического анализа.

СПИСОК ЛИТЕРАТУРЫ

1.  Голуб -экономическая статистика. – М.: Гуманит. изд. центр ВЛАДОС, 2009.

2.  , , Гаврилов . – СПб.: Питер, 2007.

3.  , Шпаковская -экономическая статистика: Учебник. – М.: Юристъ, 2009.

4.  Социальная статистика: Учебник / под ред. . – М.: Финансы и статистика, 2008.

5.  Статистика: Учеб. пособие / под ред. . – М.: Финансы и статистика, 2009.

6.  Статистика: Учеб. пособие / под ред. . – М.: ИНФРА-М, 2008.

7.  Статистика: Учебник / под ред. – М.: Высшее образование, 2007.

8.  Теория статистики: учебник / под ред. . – М.: Финансы и статистика, 2007.

9.  Юдина : Учебно-методическое пособие. – Владивосток: Изд-во ВГУЭС, 2010.

10.  Экономика и статистика фирм: Учебник / под ред. . – М.: Финансы и статистика, 2007.

11.  Экономическая статистика: Учебник / под ред. . - М.: ИНФРА-М, 2009.