Станица Советская
Новокубанского района
Использование информационных технологий на уроке математики как средство повышения его эффективности
Хочется верить, что заветная мечта каждого творчески работающего педагога – научить ребенка видеть необычное в обычном, чтобы вся дальнейшая жизнь каждого ребенка стала непрерывным открытием. И если ты учитель математики, то гораздо ближе находишься к исполнению этой мечты. У тебя есть возможность создавать условия для познания математики как уникального языка, описывающего все явления окружающего мира и одновременно являющегося инструментарием, способствующим описанию математической модели любого проекта. Подтверждение данной гипотезы нахожу в федеральном компоненте государственного образования, в котором определены цели математического образования учащихся:
-овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин;
-формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Поэтому, чтобы учащиеся овладевали системой математических знаний и умений, необходимо очень серьезно относится к обобщению и систематизации получаемых знаний по каждой теме, всему курсу обучения. Занимаясь исследовательской и экспериментальной деятельностью в течение ряда лет в области информатизации образования, приходишь к заключению, что далеко не всегда учитель уделяет серьезное внимание систематизации знаний учащихся. Большую часть своих усилий он направляет на то, чтобы добиваться запоминания учебной информации, выполнения заданий по алгоритму, образу и подобию.
Формируя информационную культуру учащихся, добиваясь от них понимания того, что без системы понятий невозможно успешное освоение любого учебного курса, а тем более курса математики, возможен переход на новое качество образования. Когда каждый обучающийся сознательно использует в своей учебной деятельности принципы информационного взаимодействия, тогда использование информационных технологий в образовательном процессе позволяет расширить возможности его эффективности.
Творческой группой педагогов, руководителем которой я являюсь, накоплен достаточный опыт по формированию информационной культуры всех участников образовательного процесса. Данный опыт описан и внесен в краевой банк передового педагогического опыта. И именно этот опыт позволяет сегодня говорить о создании авторской информационно-педагогической технологии обобщающего урока. Почему выбор был остановлен именно на обобщающем уроке? Почему использование данной технологии так необходимо в проведении уроков по математике?
Российская педагогика и практика накопила огромный опыт в организации образовательного процесса, но все больше и больше детей проявляют свое нежелание обучаться в обычной школе, говорят о том, что в школе стало не интересно и скучно учиться. Неужели современные дети потеряли интерес к новому, необычному. Неужели они ничего не хотят знать? Конечно, нет! Понаблюдайте за ними на переменах. С каким интересом они обсуждают возможности нового мобильного телефона или радуются еще за одного из своих одноклассников, которому родители подарили компьютер. Среди стайки ребят мы увидим и тех, кому часто скучно на уроке, кто упорно отказывается заниматься учебным трудом. И неправда, что они используют телефоны и компьютеры только для игр и развлечений. Есть и такие, но в основном ребята с жадностью осваивают все новые и новые возможности своего компьютера или телефона.
Сегодня мы все перегружены информацией, и поэтому главной задачей школы должно стать стремление научить каждого ребенка ориентироваться в этом нарастающем потоке информации, научить его отсеивать ненужное, искать достаточное для обоснования необходимого. Главным инструментом мыследеятельности по любой теме является система основных понятий. Определив систему и каждое понятие, убедившись в согласованности тезауруса учителя и учащихся, можно говорить об освоении учащимися социального опыта, т. е. знаний, умений и навыков в этой области. Именно систематизация знаний учащихся помогает учителю создать наиболее благоприятные условия и возможности для реализации их способностей с учетом индивидуального восприятия информации и способов работы с нею. Преимущество современного урока математики в условиях информатизации заключается в свободе выбора учителем методик и технологий, учебников и программ. Но результативность педагогической деятельности всегда зависела, и будет зависеть от того, насколько умело педагог умеет организовать работу с учебной информацией, а главным критерием эффективности учительского выбора по-прежнему остается качество образовательного процесса и знаний учащихся.
Поэтому творческий учитель на основе использования информационных технологий способен организовать современный урок таким образом, когда организация познавательной деятельности учащихся носит технологический, развивающий эффект. Существенная перемена в структуре образования может быть охарактеризована как перенос центра тяжести с преподавания в процессе обучения на учение. Это не обыкновенное «натаскивание» учеников, не экстенсивное увеличение знаний, а творческий подход к обучению всех участников образовательного процесса. На помощь учителю приходят коллективные формы обучения, и тогда учащиеся, которые испытывают затруднения в освоении математических понятий, получают дополнительные возможности для получения консультации, помощи, поддержки, а «математики» - дополнительную возможность реализовать себя. И именно информационные технологии позволяют осуществить этот переход, т. к. появляется потребность для более широкой дифференциации, индивидуализации и интеграции образовательного процесса. Новые возможности для организации систематического контроля над усвоением учебной информации не только через различные виды тестирования, но и подготовки таких видов заданий, которые позволяют видеть результат сразу после его выполнения, переводят образовательный процесс на более высокий уровень.
Сотрудничество обучаемых и обучающихся, их взаимопонимание является важнейшим условием образования. Серьезный подход к подбору приемов педагогических техник при конструировании обобщающего урока математики позволяет создать обстановку взаимодействия и взаимной ответственности. Положительный результат образовательного взаимодействия возможен только при наличии высокой мотивации.
В условиях информатизации образования и внедрения информационно-педагогических технологий системный подход к организации работы с информацией позволяет решить множество проблем, а творческий подход определяется научным выбором лучшего из возможного. Т. е., речь здесь уже должна идти об изобретении новых информационно-педагогических технологий. Следовательно, необходима теоретическая подготовка учителя, его четкое представление структуры, целей и задач образования в условиях внедрения информационных технологий, чтобы использование ИКТ на уроках не превратилось в новомодную игрушку. По мере реализации идей эксперимента выявлено, что осознанное использование приемов педагогических техник необходимо не только учителю, но и учащимся, что необходима адаптация учащихся к новым методам работы с информацией. И когда технологическая культура учащихся повышается вместе с учительской, учитель становится организатором учебного процесса, познавательной активности учащихся. Тогда нет места пассивности на уроке ни одной из сторон взаимодействия, и деятельностный подход становится основным в ходе обретения знаний.
В чем же проявляется технологическая культура учителя и учащихся, какие проблемы возникают при реализации принципов информационного взаимодействия при организации образовательного процесса с использованием информационных технологий на уроке математики? Это, прежде всего, овладение методикой конструирования сценария обобщающего урока, основанного на использовании принципов информационного взаимодействия. Одним из основополагающих моментов информационно-педагогической технологии обобщающего урока является выстраивание системы понятий, привлекательная форма подачи предлагаемой к изучению информации и организация процесса сотворчества учителя и учащихся. Установление новых связей между понятиями и идеями; четкая и грамотная постановка учебной, воспитательной и развивающей целей урока и моделирование на их основе образовательной деятельности; учет особенности конкретного классного коллектива и каждого его члена при отборе приемов педагогических техник позволяет максимально реализовать поставленные цели на каждом этапе урока. Ни в коем случае не следует увлекаться набором различных приемов и способов организации учебной работы: только согласованность и логичность отбора позволит создать целостность и завершенность урока, а использование информационных технологий повысить его эффективность.
Конкретные находки в методике преподавания математики кажутся нередко стороннему наблюдателю малозначащими. Между тем именно они являются важным средством активизации мышления школьников и основой системы работы каждого учителя. Это позволяет говорить как об улучшении качества работы учителя, так и качества знаний учащихся. Применение математических знаний учащимися в школьном курсе в основном сводится к решению задач, в которых уже сформулирован вопрос. В жизни же чаще требуется умение самому эти вопросы формулировать и, применяя имеющиеся знания, находить на них ответы.
Поэтому работа по созданию системы математических упражнений, включающих в себя задания различного характера, в том числе и задания по составлению условий математических задач, алгоритмов исследований, математических моделей, проектов и т. д. способствует повышению педагогической компетентности и мастерства учителя. Такая работа возможна только тогда, когда учитель совместно с учащимися систематически проводит анализ выполненных работ, допущенных ошибок и причин их допущения, т. е. устанавливает не только неусвоенные понятия и их свойства, но проводит работу по упреждению возможных ошибок. Для организации работы такого характера необходимо умение по проектированию полноты системы математических упражнений. Эта идея берет свое начало в методе укрупненных дидактических единиц, которым я в свое время была увлечена и с большим интересом изучала и применяла на практике.
В основе всей психической деятельности человека находятся циклические, кольцевые процессы, поток информации распространяется по замкнутым путям. Характерная особенность кольцевого процесса заключается в том, что он может быть начат с любого звена цикла умозаключений и, тем не менее, привести к проявлению всех элементов и связей цикла.
Создание полноты системы математических упражнений по теме «Уравнение» при обобщении знаний учащихся 5-го класса способствует расширению и укрупнению этих знаний. Поэтому предлагаемая методика не разбивается на модули и блоки, а реализуется последовательно и планомерно при обращении к этой теме в учебном плане каждого конкретного класса, или при организации повторения, индивидуальных или групповых занятий.
Если начальная школа основательно занимается формированием понятия «Натуральные числа» и отрабатывает с учащимися вычислительные умения, навыки по решению задач, то понятие «Уравнение» очень часто для ученика начальной школы остается непонятым. (В лучшем случае учитель добивается зазубривания алгоритмов решения всех типов элементарных уравнений.) И на основе этого непонимания учитель начальной школы отрабатывает с учащимися умения решать элементарные уравнения. В пятом классе непонимание многих учащихся в этой области знаний переходит в стойкое нежелание разобраться с этой темой.
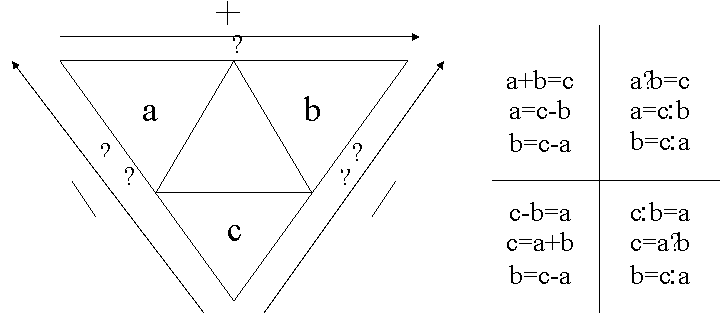

Начальная школа дает учащимся понятия «Выражение», «Равенство», «Уравнение», но учащиеся еще очень долго путаются в них. Именно поэтому учащиеся допускают логические ошибки при оформлении решения уравнения. Например:
2х + 3 = 5 = 5 – 3;
2х = 8 = 8 : 2 = 4 и т. п.
Поэтому очень важно на раннем этапе расширения знаний учащихся об уравнении привести первоначальные математические знания пятиклассников в систему:
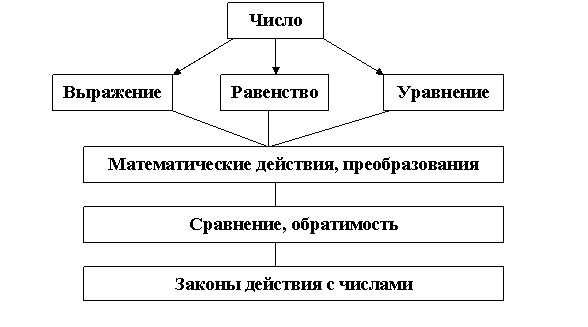

Действия - основной вид математических вычислений.
Преобразование – превращение из одного вида в другой.
Обратимость – способность после определенного круга развития возвращаться к первоначальному состоянию.
Работа с данной таблицей может быть организована по-разному:
- если в классе достаточно сильных учащихся, то таблица заполняется на уроке совместно с учащимися;
- если в классе много слабых учащихся, то работу по систематизации знаний учащихся лучше организовать с готовой таблицей.
И в том, и в другом случае для этого используются следующие вопросы:
1. Какое понятие в математике является основным? (число)
2. Какое выражение называется числовым?
3. Какое выражение называется буквенным?
4. Дайте определение равенства?
5. Что называется уравнением?
6. Какие математические операции вы можете выполнять с данными понятиями? (Найти значение числового и буквенного выражения, решить уравнение). И т. д.
Очень важно при этом обратить внимание учащихся на то, что сложение одинаковых слагаемых можно заменить умножением и установить подобную зависимость на вычитание и деление и отметить, что к этому замечанию обязательно будет возвращение. После повторения всех компонентов при сложении, вычитании, умножении и делении необходимо повторить нахождение каждого компонента и результат повторения предложить занести в таблицу, предложив обозначить числа буквами а и в, а результат выполненных действий буквой с:
а + в = с а = с – в в = с - а | а * в = с а = с : в в = с : а |
а – в = с а = с + в в = а - с | а : в = с а = с * в в = а : с |
Далее предлагается учащимся внимательно изучить полученную таблицу и обратить внимание на то, что при нахождении неизвестных компонентов при сложении и умножении используется одно и то же действие, обратное данному. При нахождении неизвестных компонентов при вычитании и делении используются и данные действия, и им обратные. С этого момента и начинается путаница при решении элементарных уравнений. Поэтому учащимся предлагается провести небольшую исследовательскую работу. Чтобы эта работа была более продуктивной, предлагаются заранее следующие вопросы:
1. Какие из компонентов в равенствах а – в = с и а: в =с больше?
2. Может ли уменьшаемое (делимое) быть больше вычитаемого (делителя?)
3. Можно ли большее число найти действием вычитания (деления)?
4. Может ли слагаемое (множитель) быть больше суммы (произведения).
Наиболее результативной такая работа бывает при групповой форме организации. Причем учащимся предлагается сначала поразмышлять самостоятельно, а затем свои выводы согласовать в группе и только после этого их огласить. Чтобы закрепить результаты исследований, каждой группе предлагаются неверно решенные уравнения. Учащиеся анализируют решение уравнения, указывают ошибку и называют причину допущенной ошибки; затем решают уравнение и называют правильный ответ. Например:
1. Проанализируйте решение уравнения:
54 – х = 42, Проверка:
х = 54 + 42, 54-96=42
х = 96.
Ответ: х = 96.
Ответ ученика.
В решении уравнения допущена ошибка при нахождении вычитаемого, которое находится сложением уменьшаемого и разности и не сделана проверка, а только подставлено найденное значение буквы в данное уравнение.
Чтобы найти вычитаемое, надо из уменьшаемого 54 вычесть разность 42. Вычитаемое равно 12. Из 54 вычесть 12, получаем 42. Ответ: х = 12.
Для формирования умения учащихся решать элементарные уравнения, эффективно использовать задания следующего типа:
1. Заполни квадраты: ![]()
![]()
5 + = 12 + 12 = 46
![]()
![]() 34 - = 20 - 15 = 6 и т. д.
34 - = 20 - 15 = 6 и т. д.
2. Заполни пропуски:
___ + 25 = 49 73 - __ = 64
___ - 42 = 31 67 + __ = 105 и т. д.
3. Составь уравнение:
а) 7; 35; а.
(35 : а = 7; 35 – а = 7; 7 + а = 35; а + 7 = 35; 7 * а = 35; а * 7 = 35.)
б) 28; 5; х.
(28 – х = 5; х + 5 = 28; 5 + х = 28.) и т. д.
При переходе к решению сложных уравнений, когда используются свойства равенств и учащиеся знакомятся с переносом членов уравнения из одной части в другую, работа по систематизации знаний учащихся должна переходить на более высокий уровень. Учащиеся должны очень четко представлять зависимость между всеми компонентами при решении любых уравнений, только тогда их знания будут прочными, а навыки при решении любых уравнений не будут получать сбой всякий раз, когда прошло достаточно времени с момента рассмотрения данной темы.
Учитель математики МОУ СШ №9,
Руководитель МОЭП
,
высшая квалификационная категория.




