КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Теоретическая механика»
Задание 1: Железнодорожный вагон ![]() массой m получив в точке A начальную скорость VA движется по рельсам, которые на различных участках либо горизонтальны, либо наклонны под углом a к горизонту (рис. 1). Длина участка AB = ℓ. Считается, что на всех участках на вагон действует сила трения (коэффициент трения f), а на участке BC еще и сила сопротивления среды R, зависящая от скорости V вагона. Считать, что в точке B вагон меняет только направление скорости, сохраняя ее модуль.
массой m получив в точке A начальную скорость VA движется по рельсам, которые на различных участках либо горизонтальны, либо наклонны под углом a к горизонту (рис. 1). Длина участка AB = ℓ. Считается, что на всех участках на вагон действует сила трения (коэффициент трения f), а на участке BC еще и сила сопротивления среды R, зависящая от скорости V вагона. Считать, что в точке B вагон меняет только направление скорости, сохраняя ее модуль.
Рассматривая вагон в виде материальной точки, определить закон изменения скорости и закон движения вагона на участке AB, а также закон изменения скорости на участке BC. Единицу измерения коэффициента сопротивления m, следует определить самостоятельно из формулы силы сопротивления R.
Схемы движения железнодорожного вагона изображены на рис. 1., а необходимые для решения данные приведены в табл. 1.
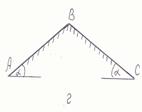
Рис. 1 – Схема движения вагона к заданию № 1
Исходные данные к заданию № 1 по динамике материальной точки
Номер варианта | Рис.1 (а – е) |
т |
м/с |
град. |
м |
|
кН |
|
28 | г | 40 | 10 | 7 | 300 | 0,07 |
| 0,05 |
РЕШЕНИЕ
1. Рассмотрим движение вагона на первом участке АВ. Изображаем его на рисунке (в виде точки) в текущем (промежуточном положении). Указываем все действующие на вагон силы – это сила трения, Fтр, направленная против вектора скорости V; сила тяжести Р, направленная вертикально вниз; нормальная реакция N, направленная перпендикулярно рельсам (линии АВ). Строим декартову систему координат Аху, взяв начало в начальном положении вагона и проведя ось Ах по АВ.
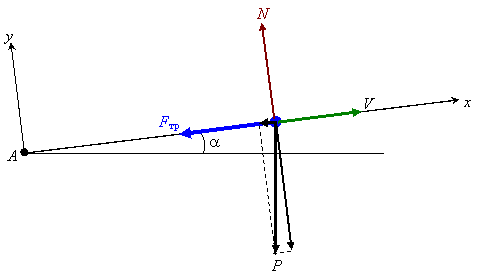 |
Схема сил, действующих на вагон на участке АВ.
2. Составим дифференциальные уравнения движения вагона в проекциях на выбранные оси.
В соответствии с законом Ньютона:
a×m = –Fтр – Р×sina, распишем силы.
Вес вагона Р = m×g, где g ≈ 9,81 м/с2 – ускорение свободного падения; сила трения Fтр = f×N, в свою очередь нормальная реакция от веса вагона N = P×cosa = m×g×cosa.
Учитывая, что ускорение это первая производная от скорости и вторая от пройденного пути, получаем:
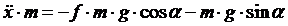 , сокращаем массу и окончательно получаем дифференциальное уравнение, описывающие движение вагона на участке АВ.
, сокращаем массу и окончательно получаем дифференциальное уравнение, описывающие движение вагона на участке АВ.
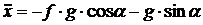 (1)
(1)
3. Интегрируем полученное уравнение по времени
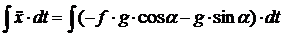 , учитываем, что интеграл от второй производной равен первой производной, т. е.
, учитываем, что интеграл от второй производной равен первой производной, т. е. 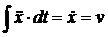 – скорость вагона. Кроме этого, во второй части уравнения все величины постоянные, интеграл от постоянной величины равен этой величине, умноженной на время, плюс постоянная интегрирования С1.
– скорость вагона. Кроме этого, во второй части уравнения все величины постоянные, интеграл от постоянной величины равен этой величине, умноженной на время, плюс постоянная интегрирования С1.
Получаем
v = – g(f×cosa + sina)×t + С1 (2)
Получили закон изменения скорости вагона, он движется равнозамедленно с ускорением а = – g(f×cosa + sina).
Проинтегрируем полученное уравнение (2), в результате после интегрирования первой производной получаем саму величину, т. е. получаем закон изменения пути, х.
Интеграл от t будет равен 0,5t2.
Получаем
òv×dt = ò[– g(f×cosa + sina)×t + С1]×dt
x = – g(f×cosa + sina)×òt×dt + òС1×dt
x = – 0,5×g(f×cosa + sina)×t2 + С1×t + C2 (3)
здесь С2 – вторая постоянная интегрирования.
4) Для определения постоянных интегрирования запишем начальные условия движения вагона на первом участке АВ.
В момент времени t = 0 вагон имел начальную скорость v0 = V и его путь равнялся нулю, он находился в начале координат, х0 = 0.
Подставляем t = 0 в полученные уравнения 2 и 3:
v0 = – g(f×cosa + sina)×0 + С1
Получаем С1 = V
x0 = – 0,5×g(f×cosa + sina)×02 + V×0 + C2
C2 = 0.
5) Находим окончательные законы изменения скорости и движения на участке АВ:
v = – g(f×cosa + sina)×t + V (4)
x = – 0,5×g(f×cosa + sina)×t2 + V×t (5)
Теперь подставляем значения и получаем:
v = – 9,81(0,07×cos7° + sin7°)×t + 10 (6)
или v ≈ 10 – 1,877×t
Для последующего решения потребуется скорость и ускорение в т. В, определим их.
Из уравнения (5) для точки В находим время, за которое вагон доедет до этой точки:
xВ = – 0,5×g(f×cosa + sina)×tВ2 + V×tВ, где хВ = ℓ.
Подставляем значения:
300 + 0,5×9,81×(0,07×cos7° + sin7°)×tВ2 – 10×tВ = 0
0,93855985×tВ2 – 10×tВ + 300 = 0, решаем квадратное уравнение:
tB = 5,327 ± j17,066 – уравнение не имеет физически реализуемых корней.
Определим время, при котором скорость вагона станет нулевой.
0 ≈ 10 – 1,877×t0
t0 = 5,327 с.
За это время вагон пройдёт
Х0 = – 0,5×g(f×cosa + sina)×t02 + V×t0 = 50,558 м – он не доходит до верхней точки В и скатится назад.
Чтобы продолжить решение задачи и выполнить вторую часть расчётов сократим заданный путь до 50 м, ℓ = 50 м.
Тогда xВ = – 0,5×g(f×cosa + sina)×tВ2 + V×tВ,
Подставляем значения:
50 + 0,5×9,81×(0,07×cos7° + sin7°)×tВ2 – 10×tВ = 0
0,93855985×tВ2 – 10×tВ + 50 = 0, решаем квадратное уравнение:
tB1 = 5,265 с, tВ2 = 99,257 с, оставляем первый корень, так как второй не имеет физического смысла, за это время вагон остановится.
Получаем скорость в т. В
VB = – 9,81(0,07×cos7° + sin7°)×5,265 + 10 = 0,117 м/с.
6) Рассмотрим движение вагона на втором участке ВС аналогично тому, как это было сделано для участка АВ. Основные изменения – изменится направление действия силы тяжести и добавиться сила сопротивления R, которая зависит от скорости вагона.
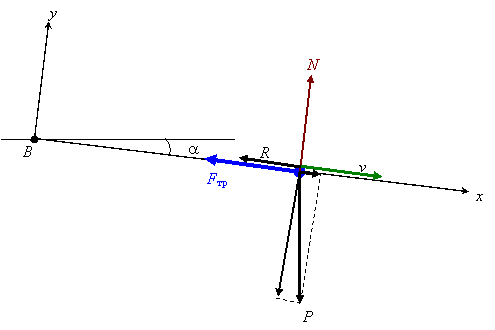 |
Схема сил, действующих на вагон на участке ВC.
7) Для участка ВС строим новую систему координат Вху взяв начало в точке В и проведя ось Вх по ВС.
Составляем дифференциальные уравнения движения вагона в проекциях на указанные оси.
В соответствии с законом Ньютона:
a×m = –Fтр + Р×sina – R, добавилась сила R = m×v2 = ![]() .
.
Получаем для участка ВС:
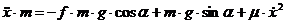 (7)
(7)
8) Решаем неоднородное нелинейное дифференциальное уравнение второго порядка.
Для упрощения выкладок сразу подставим постоянные величины:
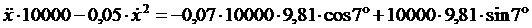
10000×x" – 0,05×(x')2 = 1,87712×104
Решаем однородное уравнение:
10000×x" – 0,05×(x')2 = 0
Водим новую переменную (скорость)
x' = ![]() = v(t), тогда x" = v'(t), это позволит понизить порядок уравнения:
= v(t), тогда x" = v'(t), это позволит понизить порядок уравнения:
Получаем:
10000×v' – 0,05×v2 = 0, сокращаем
Переписываем через дифференциалы и разделяем переменные
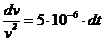
Интегрируем полученное уравнение
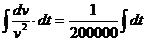
–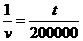 + C1, где С1 – постоянная интегрирования.
+ C1, где С1 – постоянная интегрирования.
Получаем:
v(t) = ![]() , переобозначаем постоянную интегрирования
, переобозначаем постоянную интегрирования
v(t) = 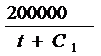 (8),
(8),
или
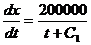 , опять разделяем переменные и интегрируем
, опять разделяем переменные и интегрируем
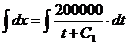
x = 200000×ln(t + C1) + C2 (9)
Получили решение однородного уравнения (9).
Для получения общего решения уравнения (7) необходимо к решению однородного уравнения прибавить частное решение неоднородного уравнения ![]() . Для неоднородного уравнения с правой частью в виде константы, частное решение ищут в виде этой константы,
. Для неоднородного уравнения с правой частью в виде константы, частное решение ищут в виде этой константы, ![]() = 18771,2.
= 18771,2.
Первая и вторая производная от постоянной равны нулю и мы очевидно получаем после подстановки в исходное уравнение частного решения
10000×(![]() )" – 0,05×(
)" – 0,05×(![]() ')2 +
')2 + ![]() = 1,87712×104
= 1,87712×104
10000×0 – 0,05×02 + 18771,2 = 1,87712×104 – тождество.
Общее решение
x = 200000×ln(t + C1) + C2 + 18771,2 (10)
9. Для участка ВС принимаем новый отсчет времени от начального момента t = 0. Найходим с помощью начальных условий движения постоянные интегрирования.
При t = 0, х = 0 и v(0) = VB = 0,117 м/с.
Из (8) получаем
0,117 = 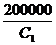 , С1 = 200000/0,117 = 1709916,5.
, С1 = 200000/0,117 = 1709916,5.
Окончательно искомый закон изменения скорости вагона на участке ВС:
v(t) = 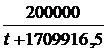 .
.
Задание 2: Машинист электровоза посредством контроллера увеличивает мощность тяговых двигателей так, что модуль силы тяги FT возрастает согласно уравнению FT = 22×t + 0,3×t2. 2. Масса электровоза m = 140 т начальная скорость V0 = 0. Модуль силы сопротивления движению постоянен и равен R = mG, где m = 0,017 – коэффициент сопротивления; G– вес электровоза.
Принимая электровоз за материальную точку, определить момент времени, когда он тронется с места, а также закон изменения скорости и уравнение движения. Участок пути считать горизонтальным.
РЕШЕНИЕ.
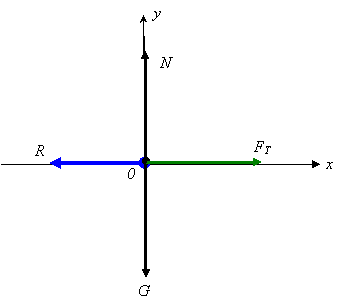 1. Изображаем электровоз на рисунке (в виде материальной точки) в произвольный момент времени и указываем все действующие на него силы.
1. Изображаем электровоз на рисунке (в виде материальной точки) в произвольный момент времени и указываем все действующие на него силы.
На электровоз действует сила тяжести G = m×g; сила тяги FT и сила сопротивления R, которая постоянна и равна R = mG = 0,017×140000×9,81 = 2,335×104 Н. Считаем, что в эту силу включены все силы сопротивления, включая силу трения. Так же на электровоз действует сила нормальной реакции, которая при горизонтальном расположении электровоза будет равна его весу N = G.
2. Определим момент времени t1 когда электровоз трогается с места. Условие трогания, равенство силы тяги и сопротивления:
t = t1
R = FT;
m×m×g = 22×t1 + 0,3×t12
22×t1 + 0,3×t12 – 2,335×104 = 0
Решаем квадратное уравнение и получаем корни:
t1 = 244,706 с и t1 = –318,039 с – этот корень отбрасываем, как физически нереализуемый.
Электровоз тронется с места через t1 = 244,706 c ≈ 4 мин.
3. Принимаем за начало координат точку начального положения электровоза и направляем ось Ох по горизонтальному участку пути.
В соответствии с законом Ньютона составляем дифференциальное уравнение движения электровоза в проекции на ось Ох:

x"×m = 22×t1 + 0,3×t12 – m×m×g
x"×140000 = 22×t1 + 0,3×t12 – 2,335×104 (1)
Интегрируем дважды дифференциальное уравнение (1) и находим закон изменения скорости и закон движения электровоза.
140000òx"×dt = ò(22×t1 + 0,3×t12 – 2,335×104)×dt
140000×x' = 11×t2 + 0,1×t3 – 23347,8×t +C1 (2)
В момент трогания электровоза его скорость равна нулю, отсюда запишем начальные условия для нахождения С1:
t = t1 = 244,706 c
x'(t1) = 0
140000×0 = 11×t12 + 0,1×t13 – 23347,8×t1 +C1
C1 = (23347,8 – 11×t1 + 0,1×t12)× t1 = (23347,8 – 11×244,706 + 0,1×244,7062)×244,706 = 3589330,811 ≈ 3589330,8
Подставляем полученное значение и получаем искомое уравнение для скорости электровоза:
140000×v(t) = 11×t2 + 0,1×t3 – 23347,8×t +3589330,8
v(t) = 7,1429×10–7×t3 + 7,8571×10–5×t2 – 0,16677×t + 25,63808 м/с (3)
или
v(t) = 2,57144×10–6×t3 + 2,82856×10–5×t2 – 0,60037×t + 92,29709 км/час
Теперь находим закон изменения пути:
140000òx'×dt = ò(11×t2 + 0,1×t3 – 23347,8×t +358930,8)×dt
140000×x = 3,66667×t2 + 0,025×t4 – 11673,9×t2 + 25,63808 ×t + C2
Запишите начальные условия движения для момента трогания электровоза, его путь равен нулю:
t = t1 = 244,706 c
x(t1) = 0
140000×0 = 3,66667×t13 + 0,025×t14 – 11673,9×t12 +3589330,8×t1 + C2
С2 = 11673,9×244,7062 – 3,66667×244,7062 – 0,025×244,7064 – 3589330,8×244,706 = – 3,22658×108
140000×x = 3,66667×t2 + 0,025×t4 – 11673,9×t2 +3589330,8×t – 3,22658×108
x = 1,78571×10–7×t4 + 2,61905×10–5×t3 – 0,083385×t2 + 25,63808×t – 2304,69767 м (4)
Уравнения (3) и (4) – искомые законы изменения скорости и уравнение движения электровоза.
Задание 3: Механическая система состоит из груза А массой mA = 9 кг, блока В массой mB = 3 кг; (большой радиус R = 60 см, меньший r = 40 см), цилиндра С массой mC = 19 кг и радиуса RC = 30 см и призмы D массой mD = 59 кг находящейся на горизонтальной плоскости. Трение между призмой и плоскостью отсутствует. Груз А получает перемещение SA = 1 м относительно призмы вдоль ее поверхности влево. Куда и на какое расстояние переместиться призма?
РЕШЕНИЕ
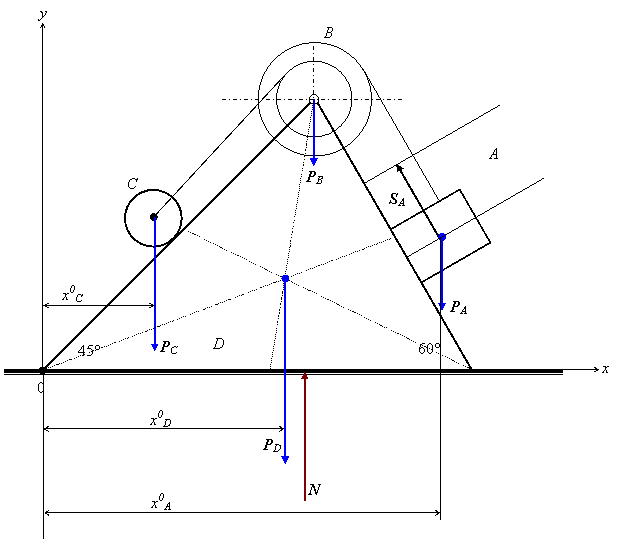 1. Построим неподвижную декартовую систему координат Оху, взяв начало О по левому краю призмы D.
1. Построим неподвижную декартовую систему координат Оху, взяв начало О по левому краю призмы D.
2. Указываем на рисунке все внешние активные силы и реакции внешних связей, действующие на данную механическую систему. К ним относятся силы тяжести всех четырех тел – РА, РВ, РС, РD, а также реакция опорной горизонтальной поверхности – ![]() . Силы тяжести всех тел приложены в их центрах тяжести (центр тяжести треугольной призмы находится в точке пересечения ее медиан), а положение точки приложения реакции связи
. Силы тяжести всех тел приложены в их центрах тяжести (центр тяжести треугольной призмы находится в точке пересечения ее медиан), а положение точки приложения реакции связи ![]() не имеет принципиального значения. В данной схеме все указанные силы направлены вдоль координатной оси у.
не имеет принципиального значения. В данной схеме все указанные силы направлены вдоль координатной оси у.
3. Составим дифференциальное уравнение движения центра масс данной системы в проекции на горизонтальную ось ![]() :
:
![]()
где: М – масса всей системы; ![]() – проекция ускорения центра масс всей системы на ось Ox.
– проекция ускорения центра масс всей системы на ось Ox.
4. Проинтегрируем дважды полученное дифференциальное уравнение, учитывая, что в начальный момент времени система находилась в покое. В результате двойного интегрирования получим:
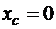 . (1)
. (1)
Равенство (1) означает, что положение центра масс системы на координатной оси ![]() остается неизменным (несмотря на то, что отдельные тела в системе переместились по сравнению с их первоначальным положением).
остается неизменным (несмотря на то, что отдельные тела в системе переместились по сравнению с их первоначальным положением).
Отсюда делаем вывод о том, что координата х0c центра масс системы вначале (когда все тела находились в покое) будет равна координате хc системы в конце (после перемещения отдельных тел в системе), т. е. будет выполняться равенство: х0c = хc.
5. Составим вторую схему, положение системы в конечном положении:
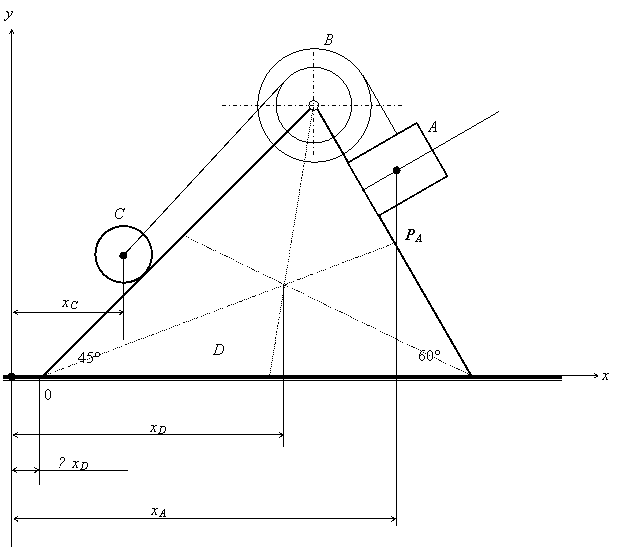
6. Воспользуемся формулами для определения координат центра масс системы вначале х0С (когда она находилась в покое) и в конце хС (когда груз А совершит перемещение SA):
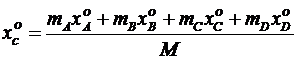 ,
,
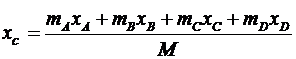 ,
,
где: mA, mB, mC, mD – массы тел A, B, C и D соответственно;
xOA, xOB, xOC, xOD – начальные координаты центров масс тел A, B, C и D;
xA, xB, xC, xD – конечные координаты центров масс тел A, B, C и D.
Начальные и конечные координаты центров масс тел определяем по рисункам. Центр тяжести призмы D находится в точке пересечения медиан, но его точное расположение неважно, необходимо найти только перемещение призмы и её направление.
На рисунке конечного положения предполагается, что после перемещения груза А по грани призмы влево на расстояние SA призма D переместится вправо на расстояние ∆xD.
![]() Обозначаем проекции на ось Ох в начальном положении:
Обозначаем проекции на ось Ох в начальном положении:
xOA = a
xOB = b
xOC = c
xOD = d
Из второго рисунка находим абсолютные перемещения и новые координаты, выражая их через заданное перемещение и проекции в начальном положении:
![]() xA = a – SA×cos60° + ∆xD
xA = a – SA×cos60° + ∆xD
xB = b + ∆xD
xC = c – SA×(r/R)×cos45° + ∆xD
xD = d + ∆xD
7. Подставляем полученные выражения в формулы для нахождения центра масс и приравниваем х0c = хc:
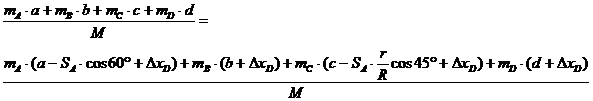
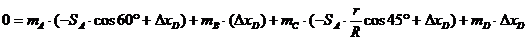
Подставляем величины и находим неизвестное перемещение:
0 = 9×(–1×cos60° + ∆xD) + 3×∆xD + 19×(–1×cos45°×40/60 + ∆xD) + 59×∆xD
∆xD = ![]() ≈ 0,199278 м.
≈ 0,199278 м.
Положительное значение величины означает, что предположение о том, что призма перемещается вправо, оказалось верным.
Призма переместится на 199,28 мм, или на 19,93 см вправо.
Задание 4: Механическая система состоит из тел, взаимосвязанных между собой нерастяжимой нитью. Под действием сил тяжести система из состояния покоя приходит в движение. Какую скорость приобретет груз ![]() , переместившись (вверх или вниз) на расстояние
, переместившись (вверх или вниз) на расстояние ![]() ? Качение цилиндра (или блока) происходит без проскальзывания с коэффициентом трения качения –
? Качение цилиндра (или блока) происходит без проскальзывания с коэффициентом трения качения – ![]() . Коэффициент трения скольжения –
. Коэффициент трения скольжения – ![]() . Радиусы инерции –
. Радиусы инерции – ![]() ,
, ![]() . Внешние радиусы –
. Внешние радиусы – ![]() ,
, ![]() . Внутренние радиусы –
. Внутренние радиусы – ![]() ,
, ![]() . Кроме того, определить с каким ускорением будет двигаться груз
. Кроме того, определить с каким ускорением будет двигаться груз ![]() в этот момент времени.
в этот момент времени.
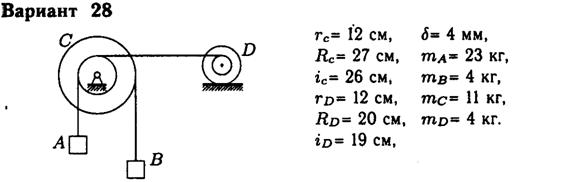 |
РЕШЕНИЕ.
1. Для определения скорости груза ![]() применим интегральную форму теоремы об изменении кинетической энергии механической системы:
применим интегральную форму теоремы об изменении кинетической энергии механической системы:
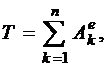
где: ![]() – текущее значение кинетической энергии системы;
– текущее значение кинетической энергии системы;

– сумма работ всех внешних сил, действующих на систему.
2. Зададим грузу А скорость VA и выразим через нее скорости других точек и тел механической системы:
– скорость точки К блока С – VK = VA = VM (так как нить нерастяжимая);
– угловая скорость блока C – ωC = VK/rC = VA/rC;
– скорость точки внешнего обода блока С, равная скорости груза В – VB = ωC×RC = VA×RC/rC;
– угловая скорость цилиндра ![]() – ωD = VM/(RD + rD) =
– ωD = VM/(RD + rD) = 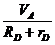 ;
;
– скорость центра масс цилиндра D – VC3 = ωD×RD = 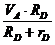 .
.
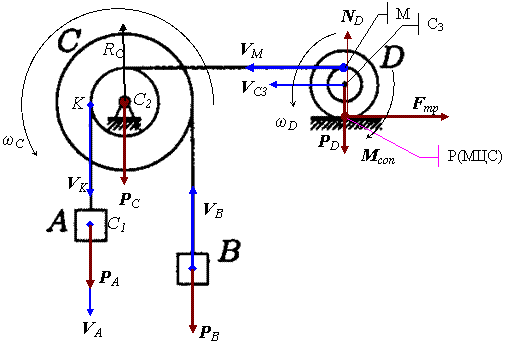 |
Точка контакта Р(МЦС) цилиндра ![]() с горизонтальной опорной поверхностью называется мгновенным центром скоростей (ее скорость всегда равна нулю).
с горизонтальной опорной поверхностью называется мгновенным центром скоростей (ее скорость всегда равна нулю).
3. Вычислим кинетическую энергию механической системы в виде функции от искомой скорости VA:
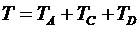 ,
,
где: TA, TB, TC, TD – кинетические энергии грузов А и В, блока С и цилиндра D соответственно.
Так как оба груза совершают поступательное движение, то их кинетическая энергия определяется по формуле:
ТА +ТВ = 0,5(mA×VA2 + mB×VB2) = 0,5[mA + mB×![]() ]×VA2
]×VA2
Так как блок C совершает вращение вокруг неподвижной оси C2, то его кинетическая энергия определяется по формуле:
TC = 0,5×JC2×ωC2 = 0,5×mC×iC2×VA2/rC2
Так как цилиндр ![]() совершает плоскопараллельное движение, то его кинетическая энергия определяется по формуле:
совершает плоскопараллельное движение, то его кинетическая энергия определяется по формуле:
TD = 0,5×mD×VC32 + 0,5×JC3×ωD2 = 0,5×[mD×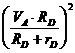 + mD×iD2×
+ mD×iD2×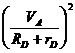 ] =
] =
0,5×mD×[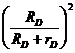 + iD2×
+ iD2×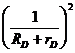 ]×VA2.
]×VA2.
Суммируем все кинетические энергии:
Т = 0,5×VA2×[mA + mB×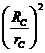 +×mC×
+×mC×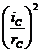 + mD×
+ mD×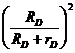 + mD
+ mD 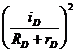 ]
]
4. Вычислим сумму работ всех внешних сил, действующих на систему при заданном перемещении груза А – S = 1 м.
– работа силы тяжести грузов – АРА + АРВ = mA×g×S – mB×g×S×RC/rC;
– работа силы тяжести блока – АРС = 0, так как SC2 = 0
– работа реакции неподвижного шарнира блока – АRC = 0, так как реакция приложена к неподвижной точке С2;
– работа силы тяжести цилиндра – АРD = 0, так как вектор силы тяжести перпендикулярен направлению перемещения;
– работа нормальной реакции горизонтальной опорной поверхности – АND = 0, так как SР(МЦС) = 0;
– работа силы трения скольжения, действующей на цилиндр – АFтр = 0, так как SР(МЦС) = 0;
– работа момента сопротивления качению – АМсоп = – Мсоп×φD =
– d×mD×g×S/(rD+RD)×
Просуммируем все работы и получим формулы для суммарной работы всех внешних сил:
А = SАi = [mA – mB×![]() – d×mD×
– d×mD×![]() ]×g×S
]×g×S
Получаем:
Т = А
0,5×VA2×[mA + mB×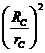 +×mC×
+×mC×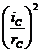 + mD×
+ mD×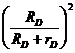 + mD
+ mD 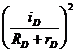 ] =
] =
[mA – mB×![]() – d×mD×
– d×mD×![]() ]×g×S
]×g×S
5. Из полученного выражения находим скорость:
VA = 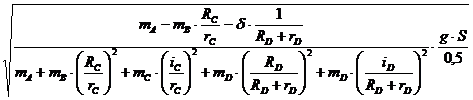 =
=
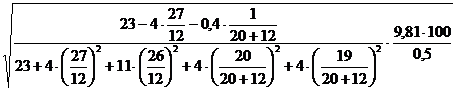 = 16,746 см/с.
= 16,746 см/с.
Получили VA = 16,746 см/с..
6. Для определения ускорения груза используем дифференциальную форму теоремы об изменении кинетической энергии системы
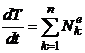 , где:
, где:![]() – суммарная мощность всех внешних сил, действующих на систему.
– суммарная мощность всех внешних сил, действующих на систему.
Выражение для суммарной мощности можно получается, если продифференцировать по времени формулу для суммарной работы этих же сил:
![]() [mA – mB×
[mA – mB×![]() – d×mD×
– d×mD×![]() ]×g×VA
]×g×VA
так как VA = dS/dt, а мощность сил по определению равна N = dA/dt.
Теперь дифференцируем по времени выражение для кинетической энергии системы
dT/dt = VA×[mA + mB×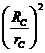 +×mC×
+×mC×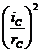 + mD×
+ mD×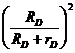 + mD
+ mD 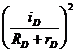 ]×(dVA/dt)
]×(dVA/dt)
где dVA/dt = aA – ускорение груза.
Подставляем полученные формулы в формулу теоремы и получаем выражение для определения требуемого ускорения:
аА = {[mA – mB×![]() – d×mD×
– d×mD×![]() ]×g×VA}/{VA×[mA + mB×
]×g×VA}/{VA×[mA + mB×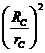 +×mC×
+×mC×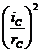 + mD×
+ mD×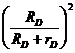 + mD
+ mD 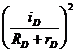 ]} =
]} =
{[mA–mB×![]() –d×mD×
–d×mD×![]() ]×g}/{[mA+mB×
]×g}/{[mA+mB×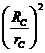 +mC×
+mC×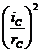 +mD×
+mD×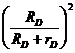 +mD
+mD 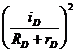 ]} =
]} =
[23–4×(27/12)–0,4×4/(12+20)]×9,81/[23+4×![]() +11×
+11×![]() +4×
+4×![]() +4
+4 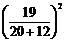 ] = 1,402 см/с2
] = 1,402 см/с2
Положительное значение ускорения говорит о том, что груз ![]() движется вниз ускоренно.
движется вниз ускоренно.





