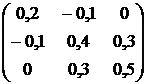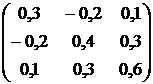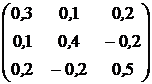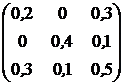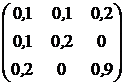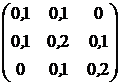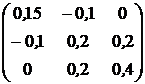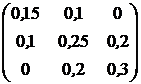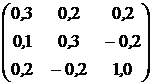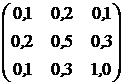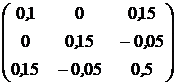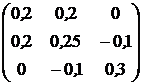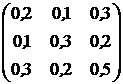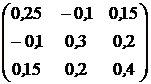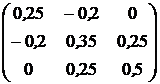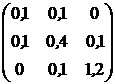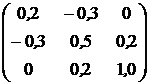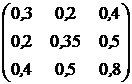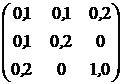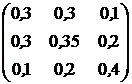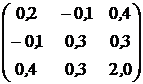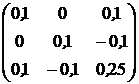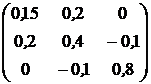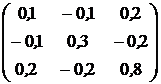З А Д А Н И Е 2

Портфель рискованных активов. Множество инвестиционных

возможностей. Эффективная граница. Касательный портфель

На рынке имеются рискованные активы трех видов с ожидаемыми доходностями: , , . Ковариационная матрица доходностей этих активов равна (см. табл.2.1).

2.1. Найти портфель с наименьшим риском, который можно составить из данных рискованных активов при условии, что:

а) короткие продажи рискованных активов разрешены;

б) короткие продажи рискованных активов запрещены.

Определить ожидаемую доходность и стандартное отклонение доходности портфеля с наименьшим риском.

2.2. Найти множество портфелей, определяющих эффективную границу множества инвестиционных возможностей при использовании данных рискованных активов в случае, если: а) разрешены короткие продажи рискованных активов, б) запрещены короткие продажи рискованных активов. В обоих случаях составить уравнение эффективной границы и ее построить.

2.3. Найти касательные портфели, соответствующие безрисковым процентным ставкам и (см. табл.2.2), при условии, что:

а) короткие продажи рискованных активов разрешены;

б) короткие продажи рискованных активов запрещены.

2.4. Определить эффективную границу множества инвестиционных возможностей при разрешенных коротких продажах рискованных активов, если инвесторы могут предоставлять кредиты под безрисковую процентную ставку , а брать ссуды под безрисковую процентную ставку .

Построить стратегию инвестирования для обеспечения ожидаемой доходности: 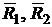и (см. табл.2.2).

2.5. Определить эффективную границу множества инвестиционных возможностей при запрещенных коротких продажах рискованных активов, если инвесторы могут предоставлять кредиты под безрисковую процентную ставку , а брать ссуды под безрисковую процентную ставку .

Построить стратегию инвестирования для обеспечения ожидаемой доходност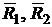и: и ?

Таблица 2.1

Продолжение таблицы 2.1

Окончание таблицы 2.1

Таблица 2.2