Информационные технологии – инструментарий для формирования знаний и умений на занятиях математики и инженерной графики
,
преподаватели
БОУ ОО СПО «Омский промышленно-
экономический колледж»
(г. Омск)
Уровень производства, научно-технический прогресс предъявляют к современному специалисту среднего звена высокие требования. Если раньше это был просто исполнитель, то сейчас это человек, который должен неординарно мыслить, быть технически грамотным, владеть современными информационными технологиями. Для специалиста – техника важно составлять грамотно техническую документацию, а для этого нужны знания многих специальных, общепрофессиональных и общеобразовательных дисциплин, таких например, как инженерная графика и геометрия.
В основе понимания форм различных деталей, способов их образования, а значит и построения чертежа этих деталей лежит пространственное мышление. Не у каждого человека оно развито в достаточной мере. И один из разделов геометрии как раз посвящен этому вопросу. Решая задачи на построение секущих плоскостей на различных геометрических телах, студенты учатся определять линии пересечения плоскостей, что несомненно пригодится при построении чертежей разрезов деталей.
Большую роль в развитии пространственного мышления оказывают такие программы как Живая Геометрия и КОМПАС 3D, которые дают возможность визуально увидеть решение задачи.
Среда Живая Геометрия представляет собой электронный аналог готовальни, с дополнительными возможностями, например, такими как создание своеобразных геометрических "мультфильмов".
Для создания чертежей используются стандартные геометрические операции такие, как - проведение прямой (луча, отрезка) через две точки, построение окружности по заданному центру и точке на окружности (или по заданным центру и радиусу), биссектрисы угла, середины отрезка, проведение перпендикулярных и параллельных прямых, фиксация пересечения прямых, окружностей, прямой и окружности.
Имеется хорошо развитая система измерений длин, углов, площадей, периметров, отношений с достаточно большой точностью, которая легко регулируется.
Система преобразований позволяет производить над объектами такие операции как отражение, растяжение, сдвиги, повороты. Во время работы с Живой Геометрией можно взять мышкой точку на созданном нами чертеже и перемещать ее по предписанной траектории. При этом изменяется длина, форма линий, то есть программа позволяет "оживлять" чертежи, плавно изменяя положение исходных точек, тем самым, первоначальное изображение принимает совсем иные формы.
Таким образом, одно из главных достоинств Живой Геометрии - возможность непрерывно менять объекты, что создает предпосылки для развития компьютерного эксперимента.
Для решения многих геометрических задач, связанных с многогранниками, полезно уметь строить на рисунке их сечения различными плоскостями.
Сечение – это изображение фигуры, которая получается при мысленном рассечении тела плоскостью. Назовем секущей плоскостью многогранника любую плоскость, по обе стороны от которой имеются точки данного многогранника.
Существует несколько методов построения сечений многогранника плоскостью: метод следов, метод внутреннего проектирования и комбинированный метод.
Суть метода следов заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры F. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры F.
Строить сечение фигуры F секущей плоскостью 
методом следов удобно в тех случаях, когда секущая плоскость задана тремя точками, ей принадлежащими, или прямой и не принадлежащей ей точкой, или двумя пересекающимися прямыми, или двумя параллельными прямыми.
Если секущая плоскость пересекает непосредственно грань многогранника, то можно также говорить о следе секущей плоскости на грани и аналогично говорить о следе на ребре. След секущей плоскости на плоскости нижнего основания условимся называть просто следом секущей плоскости. С построения именно этого следа чаще всего начинают построение сечения многогранника. Способы задания сечения весьма разнообразны. Наиболее распространенным из них является способ задания секущей плоскости тремя точками, не лежащими на одной прямой.
Решение задачи на построение сечения методом следов с помощью программы «Живая математика» выглядит следующим образом:
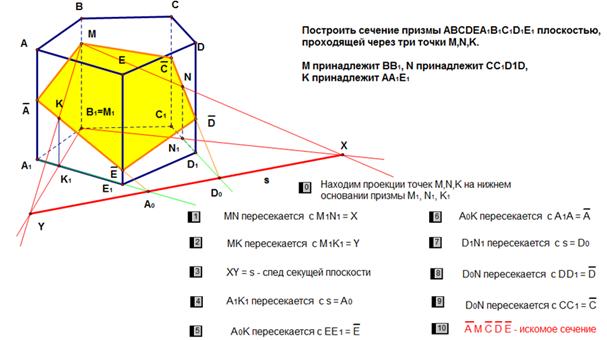
Рисунок 1 – Построение сечения методом следов
Метод внутреннего проектирования в достаточной мере является универсальным и имеет определенные преимущества по сравнению с методом следов в тех случаях, когда нужный след секущей плоскости оказывается за пределами чертежа. Вместе с тем построение при использовании этого метода получается «скученным», т. к. все они выполняются внутри многогранника (это обстоятельство послужило причиной назвать этот метод также методом вспомогательных сечений).
В тех случаях, когда сечение строится с помощью следа на плоскости нижнего основания, задавая три точки, принадлежащие непосредственно секущей плоскости, следует указать их таким образом, что бы проекции этих точек на плоскость нижнего основания строились однозначно. Сделать это можно, например, если указать, на каком ребре лежит заданная точка, или в какой грани и т. д.
При этом если многогранником, сечение которого строится, является призма, как в рассмотренном примере, то проектирование (внутреннее) на плоскость нижнего основания выполняется параллельное. Его направление определяется боковым ребром призмы. Если же многогранником является пирамида, то выполняется центральное (внутреннее) проектирование на плоскость основания. Центром проектирования является вершина пирамиды, в которой сходятся все боковые ребра.
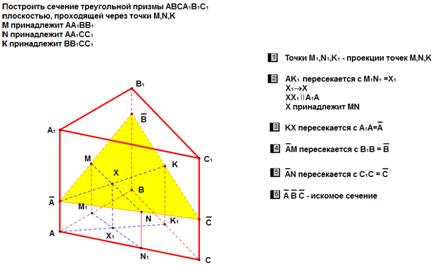
Рисунок 2 – Построение сечения методом внутреннего проектирования
Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.
Решение задачи на построение сечения комбинированным методом с помощью программы «Живая математика» выглядит следующим образом:
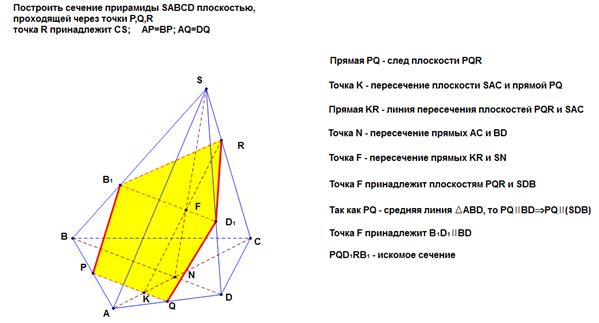
Рисунок 3 – Построение сечения комбинированным методом
В машиностроительных чертежах секущие плоскости используют при создании разрезов.
Детали машин и приборов очень часто имеют сложную форму. Они могут сочетать в себе различные геометрические тела – многогранники и тела вращения. Один из способов представления детали на чертеже – ортогональное проецирование, то есть построение видов. Если в детали имеются различной формы углубления и отверстия, целесообразно применить такое изображение как разрез.
Разрез – это мысленное сечение детали одной плоскостью или несколькими плоскостями. При выполнении разреза очень важно правильно определить точки пересечения различных геометрических тел, составляющих деталь с секущей плоскостью. Если разрез не удается построить в ручной графике, можно воспользоваться возможностями система автоматизированного проектирования.
Модель в системе КОМПАС создается с помощью различных операций над объемными элементами (рис. 4). Объемные элементы образуются путем заданного перемещения плоской фигуры (эскиза) в пространстве. Эскиз изображается на плоскости стандартными средствами чертежно-графического редактора КОМПАС-ГРАФИК.
Система построения трехмерной модели позволяет оперировать элементами вращения, элементами выдавливания, кинематическими элементами, элементами по сечениям.
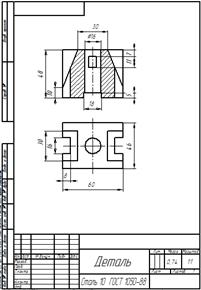По созданной модели программа позволяет получить не только виды, но и создать сечение или разрез (рис. 5).
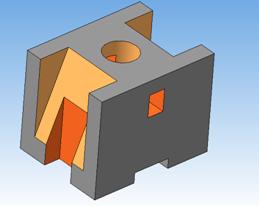
Рисунок 4 Рисунок 5
Вывод: использование информационных технологий при изучении задач на построение сечений существенно помогает в развитии пространственного воображения.
Знание методов построения сечений, способов нахождения точек и линий пересечения секущих плоскостей с различными геометрическими объектами, заложенное в общеобразовательной дисциплине помогает при изучении общепрофессиональных дисциплин, что очень важно для формирования знаний и умений будущего конкурентоспособного специалиста.
