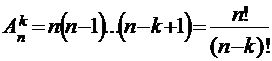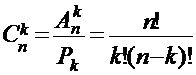ЛЕКЦИЯ 6
Тема: Основные понятия дискретной математики.
Теория вероятности.
План:
1.Основные понятия комбинаторики
2.Теория вероятностей
2.1.Случайные события и операции над ними
2.2.Определение вероятности события
2.3.Основные теоремы вычисления вероятности
1. Основные понятия комбинаторики
Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Определение 1: . Отличающиеся друг от друга порядком наборы, составленные из всех элементов данного конечного множества, называются перестановками этого множества.
Пример 1. Множество, состоящее из трех элементов {1,2,3}, имеет следующие перестановки: (1,2,3), (1,3,2), (2,3,1), (2,1,3), (3,2,1), (3,1,2). Число всех перестановок множества из п элементов обозначается Рn.
Теорема 1: (о числе перестановок). Число перестановок Рп определяется по формуле
|
Задача: Сколькими различными маршрутами можно навестить больного по 5 адресам?
Решение. Занумеруем адреса цифрами от 1 до 5. Каждому маршруту можно сопоставить один из наборов, состоящих из этих пяти цифр, например, (2,5,3,4,1). Такой набор означает, что сначала выбирается второй адрес, затем пятый, третий, четвертый и первый. Всего различных маршрутов, т. е. отличающихся порядком наборов пяти цифр будет 5! = 120.
Определение 2: Упорядоченные наборы, состоящие из k различных элементов, выбранных из данных n элементов, называются размещениями из n элементов по k.
Размещения могут отличаться друг от друга как элементами, так и порядком.
Пример 2. Различными размещениями множества из трех элементов {1,2,3} по два будут наборы (1,2), (2,1), (1,3), (3,1), (2,3), (3,2).
Число всех размещений из n элементов по k обозначается ![]() .
.
При k = п число размещений совпадает с числом перестановок.
Теорема 2 (о числе размещений). Число размещении из п элементов по k определяется по формуле
|
Задача. Студентам надо сдать 4 экзамена за 8 дней. Сколькими способами можно составить расписание сдачи экзаменов
Решение. Занумеруем дни сдачи экзаменов цифрами 1,2,.. .,8. Составлять различные расписания можно следующим образом. Сначала выберем дни для сдачи экзаменов, например, (2,4,5,7), а затем порядок сдачи экзаменов. Таким образом, нужно составить различные наборы четырех чисел из восьми, которые отличаются друг от друга не только элементами, но и порядком. Таких наборов 4: 8*7*6*5 = 1680.
Определение 3: Неупорядоченные наборы, состоящие из k элементов, взятых из данных п элементов, называются сочетаниями из n элементов по k.
Сочетания отличаются друг от друга только элементами.
Пример 3. Для множества {1,2,3} сочетаниями по 2 элемента являются {1, 2}, {1, 3}, {2, 3}.
Число всех сочетаний из п элементов по k обозначается
Теорема 3 (о числе сочетаний). Число сочетаний из п элементов по k определяется по формуле
|
Задача. В хоккейном турнире участвуют 6 команд. Каждая команда должна сыграть с каждой одну игру. Сколько игр сыграно в турнире?
Решение. Различные пары команд образуют сочетания из 6 по 2, поскольку порядок среди двух команд, играющих в одной игре, нам безразличен. Следовательно, число игр будет равно
2. Теория вероятностей
Теория вероятностей - это математическая наука, изучающая закономерности массовых случайных событий.
2.1.Случайные события и операции над ними
Случайным называется событие наступление, которого нельзя гарантировать.
Рассмотрим основные понятия теории вероятности:
Испытанием называется совокупность условий, при котором может произойти данное случайное событие.
Событие – это факт, который при осуществлении определенных условий может произойти или нет. События обозначают большими латинскими буквами А, В, С…
Опр: Событие, всегда осуществляющееся при проведении испытания, называют достоверным событием.
Опр: Когда событие не может произойти в результате испытания, его называют невозможным.
Опр: Под случайным событием, связанным с некоторым опытом, понимается всякое событие, которое при осуществлении этого опыта либо происходит, либо не происходит.
Опр: События называются несовместными, если в результате данного испытания появление одного из них исключает появление другого.
Опр: События называются совместными, если в результате данного испытания появление одного из них не исключает появление другого.
Опр: События называются равновозможными, если нет основания считать, что одно из них происходит чаще, чем другое.
События образуют полную группу событий, если в результате испытания обязательно произойдет, хотя бы одно из них и любые два из них несовместны.
События, входящие в полную группу попарно несовместных и равновозможных событий, называются исходами, или элементарными событиями.
Частным случаем событий, образующих полную группу, являются противоположные события.
Опр: Два несовместных события А и ![]() (не А) называются противоположными, если в результате испытания одно из них должно обязательно произойти.
(не А) называются противоположными, если в результате испытания одно из них должно обязательно произойти.
Операции над событиями
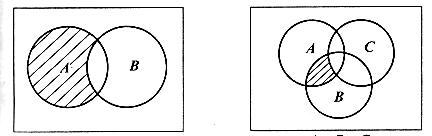
Суммой двух событий А и В называют событие С=А+В, заключающееся в наступлении события А, или события В, или события А и В одновременно.
Например, два стрелка производят по одному выстрелу. Событие А - попадание в мишень первым стрелком, событие В - попадание в мишень вторым стрелком. Событие С=А+В - попадание при выстреле первым стрелком, или вторым, или первым и вторым.
Суммой нескольких событий называют событие, которое состоит в осуществлении хотя бы одного из этих событий. Событие А+В+С заключается в осуществлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С.
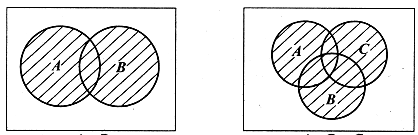
Произведением двух событий А и В называют С=АВ состоящее в совместном осуществлении (совмещении) этих событий.
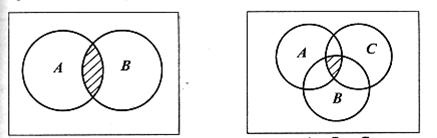
Разностью двух событий А и В (А-В) называется событие, состоящее из исходов, входящих в А, но не входящих в В.
2.2.Определение вероятности события
Случайные события реализуются с различной возможностью. Одни чаще, другие реже. Для количественной оценки возможностей реализации события вводится понятие вероятности события.
Вероятность события – это число, характеризующее степень возможности появления событий при многократном повторении события.
Вероятность является одним из основных понятий тории вероятности. Существует несколько определений этого понятия.
Классическое определение вероятности
Р (А)=![]() , где m – число благоприятных исходов, n – число всех исходов.
, где m – число благоприятных исходов, n – число всех исходов.
Свойства вероятности
1. Р(А)= 0, если А – невозможное событие
2. Р(А)=1, если А – достоверное событие
3. Вероятность случайного события: ![]()
Статистическое определение вероятности
Относительной частотой случайного события называют отношение числа появлений этого события к общему числу проведенных экспериментов:
![]()
где А – случайное событие по отношению к некоторому испытанию,
N раз проведено испытание и при этом событие А наступило в NA случаях.
Опыт с равносильными исходами
Опыт с равновероятными исходами: не существует никаких объективных оснований считать, что одно из событий является более возможным, чем другое.
Говорят, что события равновероятны и вероятность каждого из события равна 1/n.
2.3.Основные теоремы вычисления вероятности
Зная вероятности одних событий, можно вычислить вероятности других событий, если они связаны между собой.
Теорема сложения
Теорема: Вероятность наступления одного из двух несовместных событий А и В равна сумме вероятностей этих событий P(A+B)=P(A)+P(B)
Пример: в ящике находятся 20 шаров: 5 из них синих, 10 красных и 5 черных. Найти вероятность того, что при одном извлечении появится цветной шар.
Теорема: Вероятность суммы конечного числа попарно независимых событий А1, А2, …,Аn равна суме вероятностей этих событий:
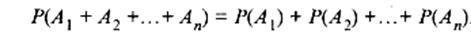
Следствие 1. Если события А1, А2, …, Аn образуют полную группу, то сумма вероятностей их равна единице:
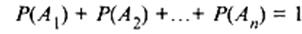
Следствие 2. Сумма вероятностей противоположных событий равна единице:
Теорема: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления:
![]()
Теорема умножения вероятностей
Событие А называют независимым от события В, если вероятность осуществления события А не зависит от того, осуществилось ли событие В или нет.
Событие А называют зависимым от события В, если вероятность осуществления события А зависит от того, осуществилось ли событие В или нет. (условная вероятность р(А/В))
Теорема: Вероятность произведения двух независимых событий называют произведение вероятностей этих событий:
P(AB)=P(A)*P(B)
Пример: Медицинская сестра обслуживает в палате двух больных. Вероятность того, что в течении часа внимания сестры потребует первый больной равна 0,2, второй больной = 0,3.Найти вероятность того, что в течение часа все больные потребуют внимания медсестры.
Теорема: Вероятность произведения двух зависимых событий А и В равна произведению одного их них на условную вероятность второго, вычисленную при условии, что первое событие осуществилось:
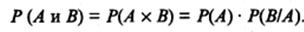
Формула полной вероятности
Формула полной вероятности является обобщением терем умножения и сложения вероятностей. Формула применяется для решения задач на определение вероятности события, которое может произойти с одним из несовместных событий, образующих полную группу.
Теорема: Вероятность события А, которое может наступить только при условии появления одного из событий Н1, Н2, …Нn, образующих полную группу попарно несовместных событий, равна сумме произведений вероятностей каждого из событий Н1, Н2, …Нn на соответствующую условную вероятность события А:
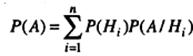
Контрольные вопросы для закрепления:
1. Какая область математики называется комбинаторикой.
2. Какие наборы множеств называются перестановками, размещениями, сочетаниями.
3. Что изучает теория вероятности?
4. Какое событие называется достоверным, случайным, невозможным
5. Приведите примеры совместных и несовместных событий.
6. Какие события называются противоположными.
7. Какие операции над событиями можно совершать, охарактеризуйте каждую операцию.
8. Дайте определение вероятности события.
9. Назовите основные теоремы вычисления вероятности.
Литература:
1. , Демидова : Компьютерные технологии в медицине. – Ростов н/Д:Феникс, 2008. -588 с. Ил.-(Среднее профессиональное образование)
2. Теория вероятности [электронный ресурс]: URL: http://www. nuru. ru/teorver. htm