Муниципальное бюджетное образовательное учреждение
средняя образовательная школа № 000
с углублённым изучением отдельных предметов
г. Уссурийска Уссурийского округа
Методические рекомендации
Решение текстовых задач
работу выполнила
учитель математики
2014 год
В разделе В![]() ( решение текстовых задач) единого государственного экзамена есть задачи на проценты. Решение таких задач вызывает у учеников определённые трудности. Данный материал поможет выпускнику успешно подготовиться к ЕГЭ по математике. Он состоит из двух частей.
( решение текстовых задач) единого государственного экзамена есть задачи на проценты. Решение таких задач вызывает у учеников определённые трудности. Данный материал поможет выпускнику успешно подготовиться к ЕГЭ по математике. Он состоит из двух частей.
Часть первая - решение восьми типов задач на проценты.
Часть вторая – задачи для самостоятельного решения с ответами.
Часть первая - решение задач.
Задача 1. Пять рубашек дешевле куртки на 5%. На сколько процентов шесть рубашек дороже куртки?
Решение:
Пусть x - стоимость 5 рубашек, y – одной куртки, т. к. 5 рубашек дешевле 1 куртки на 5%, тогда
1). y – 100%
x – 95%, получим 95y = 100x, x = ![]() y = 0,95y стоимость 5 рубашек.
y = 0,95y стоимость 5 рубашек.
2). 0,95 y : 5 = 0,19y стоимость одной рубашки, т. е. одна рубашка составляет 19% от стоимости пиджака.
3). 0,19y![]() 6 = 1,14y стоимость 6 рубашек, т. е 6 рубашек на 14% дороже пиджака.
6 = 1,14y стоимость 6 рубашек, т. е 6 рубашек на 14% дороже пиджака.
Ответ: 14%
Задача 2. Брюки дороже рубашки на 30% и дешевле пиджака на 22%. На сколько процентов рубашка дешевле пиджака?
Решение:
Пусть x – стоимость брюк, y – стоимость рубашки, z – стоимость пиджака,
т. к. брюки дороже рубашки на 30% , то x = y + 0,3y с другой стороны
брюки дешевле пиджака на 22%, то x = z – 0,22z. Получили уравнение:
y + 0,3y = z – 0,22
1,3y = 0,78z
y = 0,6z, т. е. рубашка составляет 60% стоимости пиджака или пиджак дороже рубашки на 40%.
Ответ: 40%.
Задача 3. В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 16% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Решение:
Возьмем стоимость акций в воскресенье за 1 и пусть в понедельник акции подорожали на а%, тогда
1) 1 – 100%
x – a%, получим 100x = 1а, x =![]() =0,01a на столько акции подорожали в понедельник.
=0,01a на столько акции подорожали в понедельник.
2) 1 + 0.01а столько стали стоить акции в понедельник.
3) 1 + 0.01а - 100%
y - a%, получим
y = 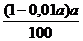 = (1 – 0,01a) 0,01a = 0,01a – 0,0001a
= (1 – 0,01a) 0,01a = 0,01a – 0,0001a![]() на столько подешевели акции во вторник.
на столько подешевели акции во вторник.
4) 1 – 0,01a - 0,01a + 0,0001a![]() = 1 – 0,0001a
= 1 – 0,0001a![]() столько стали стоить акции во вторник.
столько стали стоить акции во вторник.
По условию задачи акции стали во вторник стоить дешевле на 16%, получим уравнение:
1 – ( 1 – 0,0001a![]() ) = 0,16
) = 0,16
a![]() = 1600
= 1600
a = ![]() 40
40
Ответ: 40%.
Задача 4. Виноград содержит 90% влаги, а изюм – 5%. Сколько килограммов винограда требуется для получения 20 кг изюма?
Решение:
1) Изюм содержит 5% влаги, тогда сухого вещества в изюме будет
100% - 5% = 95%, тогда
20кг - 100%
х - 95%, получим х =![]() = 19 кг сухого вещества.
= 19 кг сухого вещества.
2) Виноград содержит 90% влаги, тогда сухого вещества в винограде будет
100% - 95% = 10%, тогда
х кг - 100%
19 кг - 10%, получим х =![]() = 190 кг
= 190 кг
Ответ: 190 кг.
Задача 5. Семья состоит из мужа, жены и их дочери – студентки. Если бы зарплата мужа увеличилась вчетверо, общий доход семьи вырос бы на 198%. Если бы стипендия дочери уменьшилась вчетверо, общий доход семьи сократился бы на 3%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Решение:
Введем переменные:
|
|
|
Составим и решим систему уравнений:
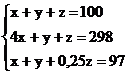
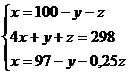 , составим и решим уравнение:
, составим и решим уравнение:
100 – y – z = 97 – y – 0,25z
100 – z = 97 – 0,25z
![]() z = 3
z = 3
z = 4 , выполним замену, получим систему:
![]()
![]()
Решим уравнение:
384 – 4y + y = 294
384 -3y =294
y = 30
Ответ: 30%
Задача 6. В сосуд, содержащий 10 литров 24-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составит концентрация получившегося раствора?
Решение:
Запишем условие задачи
![]()
![]()
![]()
![]()
![]()
![]()
раствор 10 л 5 л 15л
24% = 0,24 + 0% = 0 = х% = 0,01х
вещество 10 ![]() 0,24 0
0,24 0 ![]() 5 15
5 15 ![]() 0,01х
0,01х
составим и решим уравнение: 10![]() 0,24 + 0
0,24 + 0 ![]() 5 = 15
5 = 15![]() 0,01х
0,01х
10![]() 0,24 = 15
0,24 = 15![]() 0,01х
0,01х
0,15х = 2,4
х = 16
Ответ: 16%
Задача 7. Первый сплав содержит 5% меди, второй – 11% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
Запишем условие задачи:
![]()
![]()
![]()
![]()
![]()
![]()
Сплав х кг (х + 4) кг (х + х + 4) кг
5% = 0,05 + 11% = 0,11 = 10% = 0.1
Вещество 0,05х 0,11(х + 4) 0.1(х + х 4)
составим и решим уравнение: 0,05х + 0,11(х + 4) = 0,1(2х + 4)
5х + 11х + 44 = 20х + 40
-4х = -4
х = 1
Найдём массу третьего сплава : 1 + 1 + 4 = 6 кг
Ответ: 6 кг.
Задача 8. Смешав, 43-процентный и 89-процентный растворы кислоты и добавив 10 кг чистой воды, получили 69- процентный раствор кислоты.
Если бы вместо 10 кг воды добавили 10 кг 50- процентного раствора той же кислоты, то получили бы 73-процентный раствор кислоты. Сколько килограммов 43-процентного раствора использовали для получения смеси?
Решение:
первый случай
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
раствор х кг у кг 10 кг х + у + 10
43% = 0,43 + 89% = 0,89 + 0% = 0 = 69% = 0,69
вещество 0,43х 0,89у 0 (х + у + 10)0,69
![]()
второй случай
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
раствор х кг у кг 10 кг х + у + 10
43% = 0,43 + 89% = 0,89 + 50% = 0,5 = 73% = 0,73
вещество 0,43х 0,89у 10 ![]() 0,5 (х + у + 10)0,73
0,5 (х + у + 10)0,73
составим и решим систему уравнений:
![]()
![]()
![]()
![]()
46х = 1610
х = 35
Ответ: 35 кг.
Часть вторая – задачи для самостоятельного решения с ответами.
Задача 1. Четыре рубашки дешевле куртки на 20%. На сколько процентов шесть рубашек дороже куртки?
(Ответ: 20%)
Задача 2.Три килограмма черешни стоят столько же, сколько пять килограммов вишни, а три килограмма вишни – столько же, сколько два килограмма клубники. На сколько процентов килограмм клубники дешевле килограмма черешни?
( Ответ: 10%)
Задача 3. В четверг акции компании подорожали на некоторое число процентов, а в пятницу подешевели на то же самое число процентов. В результате они стали стоить на 81% дешевле, чем при открытии торгов в четверг. На сколько процентов подорожали акции компании в четверг?
(Ответ: 90%)
Задача 4. Виноград содержит 90% влаги, а изюм – 5%. Сколько килограммов винограда требуется для получения 82 кг изюма?
( Ответ: 779 кг)
Задача 5. Семья состоит из мужа, жены и их дочери – студентки. Если бы зарплата мужа увеличилась втрое, общий доход семьи вырос бы на 114%. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 2%. Сколько процентов от общего дохода семьи составляет зарплата жены?
( Ответ: 39%)
Задача 6. В сосуд, содержащий 7 литров 15-процентного водного раствора некоторого вещества, добавили 8 литров воды. Сколько процентов составит концентрация получившегося раствора?
(Ответ: 7%)
Задача 7. Имеется два сплава. Первый содержит 10% никеля, второй – 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?
(Ответ: 135 кг)
Задача 8. Имеется два сосуда. Первый содержит 75 кг, а второй - 30 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52% кислоты. Если же смешать равные массы этих растворов, то получится, раствор, содержащий 58% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
( Ответ: 33 кг)
Список использованной литературы.
1.Единый государственный экзамен. Математика. Тематический сборник заданий. Под редакцией ёнова ,. ЕГЭ - 2013.
2.Математика. 30типовых вариантов заданий для подготовки к единому государственному экзамену. ФИПИ – школьникам и учителям. Под редакцией ёнова, . ЕГЭ - 2013.
3. Математика. Типовые тестовые задания. Под редакцией ёнова, . ЕГЭ - 2014.




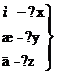 100%
100%