Контрольно-измерительные материалы по дисциплине
« Теория вероятности и математическая статистика»
Вариант 2
1. Выяснить, какой из методов можно применить для решения системы уравнений:
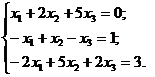
а) метод обратной матрицы; б) по формулам Крамера; в) метод Гауса.
2. Какие функции являются решениями дифференциального уравнения y|| sinx?
а) y = cosx,; б) y = - sinx+С1x+С2; в) y = ex + С; г) y = 5x + С.
3. Для сигнализации об аварии установлены два независимо работающих анализатора. Вероятность того, что при аварии сработает первый сигнализатор 0,95; второй – 0,9. Найти вероятность того, что при аварии сработает только один анализатор:
а) 0; б) 0,5; в) 0,14; г) 1.
4. Игра с «нулевой суммой» - это, если
а) выигрыш игрока А равен проигрышу игрока В; б) выигрыш игрока А равен О и выигрыш игрока В равен О.
5. Выяснить, какие из приведенных матриц являют продуктивными:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
6. Какие из перечисленных функций являются бесконечно малыми при x = 0?
а) y =![]() б) y = x10; в) y = sin
б) y = x10; в) y = sin![]() ; г) y = cos2x.
; г) y = cos2x.
7. Функция распределения непрерывной случайной величины x задана выражение:
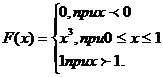
Найти вероятность попадания на участок от 0,5 до 0,8.
а) 0,5; б) 0,387; в)1; г)0.
8. Платежной матрицей называется матрица, элементами которой является
а) «выигрыши» игрока А;
б) «выигрыши» игрока В;
в) сумма «выигрышей» игрока А и игрока В.
9. Выяснить, какие из следующих операций можно выполнить над матрицами
А = ![]() и В =
и В = ![]() ;
;
а) А+В; д) В*А;
б) А1+В; е) А1*В;
в) А+В1; ж) А1*В1;
г) А*В з) В1*А1;
10. Найти сумму частных производных первого порядка функции Z = xeyb точке (1;1).
а) 1; б) 2e2; в) 2e; г) 1+e3.
11. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом равна 0,95, для винтовки без оптического прицела равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки, что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него? Какие формулы применяются для решения этой задачи?
а) формула Бернулли;
б) формула полной вероятности;
в) формула Байеса;
г) формула Пуассона.
12. Что такое оптимальный план в задаче линейного программирования?
а) допустимое решение системы ограничений, которое оптимизирует целевую функцию;
б) опорное решение задачи.
13. Дан ряд ![]()
Выбрать верные высказывания:
а) ряд сходится при x = 1 и расходится при x = 1,5
б) ряд сходится при x = 1 и расходится при x = 0
в) ряд сходится при x = 1 и расходится при x = 1
14. Какие функции являются решением дифференциального уравнения. y||=e2x?
а)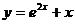 ; б)
; б) 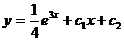 ; в)
; в) ![]() ; г)
; г) ![]()
15. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из 4x или три из шести? Какие формулы применяются для решения этой задачи?
а) формула Байеса;
б) формула полной вероятности;
в) формула Бернулли;
г) формула Пуассона.
16. Когда возникает необходимость использования симплекс – метода с искусственным базисом? Если:
а) первоначальный план является недопустимым;
б) число переменных больше пяти.
17. Какие из приведенных троек векторов образуют базис в пространстве R3?
а) ![]()
![]() ;
; ![]() .
.
б) ![]() ;
; ![]() ;
; ![]() .
.
в) ![]() ;
; ![]() ;
; ![]() .
.
г) ![]() ;
; ![]() ;
; ![]() .
.
18. Из данных рядов выбрать сходящиеся:
а) ![]() б)
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
19. В первой урне содержится 10 шаров, из них 8 белых, во второй 20 шаров, из 4 белых. Из каждой урны наудачу извлечены по 1 шару, а потом из этих двух шаров наудачу взяли один шар. Найти вероятность того, что взят белый шар. Какие формулы применяются для решения этой задачи?
а) формула Бернулли;
б) формула полной вероятности;
в) формула Байеса;
г) формула Пуассона.
20. Игра «с природой» - это, если
а) стратегии одного из игроков неизвестны;
б) цена игры равна нулю.
21. Найти решение дифференциального уравнения y||+y=sinx.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]()
22. Найти точки экстремума функции ![]() .
.
а) (-2; 0) – точка минимума;
б) (0;0) – точка максимума;
в) (1; 1) - точка минимума.
23. Бросаются две монеты. Какова вероятность, что обе монеты выпадут к верху одной и той стороной?
а) 0,5; б) 0,25; в) 0,75; г) 1.
24. Какие игры можно решать графическим методом? Если матрица игры имеет размер?
а) ![]()
![]() ,
, ![]() .
.
б) ![]() ,
, ![]() .
.
в)![]() ,
, ![]() .
.
25. Вычислить определитель 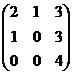
а) 4; б) 0; в) –4; г) 1.
Ключи к тестам по дисциплине
«Теория вероятностей и математическая статистика»
1 | 2 | 3 | 4 |
в | б | в | а |
5 | 6 | 7 | 8 |
а, г | б, в | б | А |
9 | 10 | 11 | 12 |
2,3 | в | в | А |
13 | 14 | 15 | 16 |
в | б, в | в | А |
17 | 18 | 19 | 20 |
б, г | а, в | б | А |
21 | 22 | 23 | 24 |
а | а | а | А |
25 | |||
в |





