Федеральное государственное автономное образовательное учреждение высшего профессионального образования
"Национальный исследовательский университет
"Высшая школа экономики"

Факультет социальных наук

Департамент социологии

Рабочая программа дисциплины

Теория вероятностей и математическая статистика

для образовательной программы «Социология»

направления подготовки 39.03.01

бакалавр

Разработчик(и) программы:

, к. физ.-мат. н., профессор, *****@***ru

, старший преподаватель, *****@***ru

, к. соц. н., доцент, *****@***ru

Одобрена на заседании департамента социологии «___»____________ 2015 г.

Руководитель департамента ________

Рекомендована Академическим советом образовательной программы бакалавриата «Социология» «___»____________ 2015 г., № протокола_________________

Утверждена «___»____________ 2015 г.

Академический руководитель образовательной программы бакалавриата «Социология»

_________________

Москва, 2015

Настоящая программа не может быть использована другими подразделениями университета и другими вузами без разрешения кафедры-разработчика программы.

Область применения и нормативные ссылки

Настоящая программа учебной дисциплины устанавливает минимальные требования к знаниям и умениям студента и определяет содержание и виды учебных занятий и отчетности.

Программа предназначена для преподавателей, ведущих данную дисциплину, учебных ассистентов и студентов направления подготовки бакалавра 39.03.01 Социология. Программа разработана в соответствии с:

·  Образовательным стандартом ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО АВТОНОМНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ «ВЫСШАЯ ШКОЛА ЭКОНОМИКИ». http://www. hse. ru/data/2015/04/09/1095226565/Бакалавриат_ОС_Социология. pdf.

·  Образовательной программой 39.03.01 «Социология» подготовки бакалавра

·  Учебным планом на весь период обучения подготовки бакалавра 2015-2020 (4 года, очная форма) по направлению 39.03.01 СОЦИОЛОГИЯ, утверждённым в 2015 г.

·  Рабочим учебным планом университета по направлению 39.03.01 «Социология» подготовки бакалавра, утверждённым в 2015 г.

  Цели освоения дисциплины

Целями освоения дисциплины «Теория вероятностей и математическая статистика» являются:

·  изучение и практическое освоение теории вероятностей, математической статистики и базовых методов статистического анализа данных в социальных науках,

·  изучение и практическое освоение компьютерной программы, применяемой для математико-статистического анализа данных (пакета SPSS),

·  приобретение понимания специфики работы с количественными данными в социальных науках, понимания типов задач, которые могут быть решены с помощью математико-статистических методов.

  Компетенции обучающегося, формируемые в результате освоения дисциплины

В результате освоения дисциплины студент должен:

-- Знать основные понятия теории вероятностей, математической статистики, методы статистического анализа данных в пределах программы курса,

-- Уметь ставить и понимать социологические задачи, которые могут быть решены с помощью методов теории вероятностей и математической статистики; понимать специфику данных, используемых в математико-статистическом анализе.

-- Иметь навыки самостоятельного статистического анализа данных на компьютере в программе SPSS.

В результате освоения дисциплины студент осваивает следующие компетенции:

  Место дисциплины в структуре образовательной программы

Настоящая дисциплина является обязательной дисциплиной профессионального цикла бакалаврской программы направления 39.03.01 Социология.

Изучение данной дисциплины базируется на следующих дисциплинах:

«Алгебра и анализ»

Основные положения дисциплины должны быть использованы в дальнейшем при изучении следующих дисциплин:

«Анализ социологических данных»

«Многомерные методы анализа данных»

«Методы анализа латентных признаков»

«Методы измерения в социологии»

«Методы классификации в социологии»

Научно-исследовательский семинар

  Тематический план учебной дисциплины

2.  , , Теория вероятностей: учебник для экономических и гуманитарных специальностей. М.: МЦНМО, 2009. С.173-185,

3.  Bluman A. Elementary statistics. McGraw-Hill, 2008. Pp.242-251

Литература дополнительная

1.  Хили Дж. Статистика. Социологические и маркетинговые исследования. СПб.: Питер, 2005

Тема 8. Теорема Муавра - Лапласа. Центральные предельные теоремы.

Теорема Муавра - Лапласа. Центральные предельные теоремы.

Литература основная

1.  , , Теория вероятностей: учебник для экономических и гуманитарных специальностей. М.: МЦНМО, 2009. С.126-136, 148-156

2.  Bluman A. Elementary statistics. McGraw-Hill, 2008. Pp.207-214, 214-220

Литература дополнительная

1.  Практическая бизнес-статистика. М.: Издательский дом «Вильямс», 2004

Тема 9. Закон больших чисел.

Закон больших чисел.

Литература основная

1.  Математико-статистические модели в социологии. М.: ИД ГУ-ВШЭ, 2007. С.64-68

2.  , , Теория вероятностей: учебник для экономических и гуманитарных специальностей. М.: МЦНМО, 2009. С.206-221, 226-233

3.  Bluman A. Elementary statistics. McGraw-Hill, 2008. Pp.251-263

Тема 10. Введение в статистический анализ данных. Выборка и генеральная совокупность. Вероятностный отбор. Простая случайная выборка (SRS).

Выборка и генеральная совокупность. Вероятностный отбор. Простая случайная выборка (SRS).

Для решения каких задач в социальных науках используется статистический анализ данных. Примеры исследований, построенных на статистическом анализе данных. Источники данных для статистического анализа: опрос, перепись, агрегированная статистика. Основные методы анализа. Обзор содержания курса. Основы работы в SPSS. Архитектура пакета. Синтаксис SPSS.

Литература основная

1.  Математико-статистические модели в социологии. М.: ИД ГУ-ВШЭ, 2007. С.19-70.

2.  Методология математического анализа данных // Социология и математика. М.: Научный мир, 2003. С.80-94.

3.  Анализ социологических данных с помощью пакета SPSS : учебное пособие для вузов. – М.: Изд. дом ГУ ВШЭ, 2007. – С.10-13

4.  Теория вероятностей и математическая статистика для социологов и менеджеров: учебник для студентов учреждений высш. образования / Науч. ред.: . М. : Издательский центр «Академия», 2014. С.8-28.

5.  , Анализ данных на компьютере: учебное пособие. – М.: ИД «ФОРУМ», 2008. – С. 15-44, 296-314.

6.  Маркетинговые исследования с SPSS: Учебное пособие. – М.: ИНФРА-М, 2007. – С. 21-41.

7.  Случайные и неслучайные выборки в социологических исследованиях // Социальная реальность. 2007. №4. С. 89-109.

8.  Основы формирования выборки: лекции для студентов направления 040100.62 (Социология) – М.: ГУ-ВШЭ, 2005, с. 8-38.

9.  Agresti, A. and Finlay, B. Statistical Methods for the Social Sciences. 4th ed. Pearson Prentice Hall, 2009. Pp.1-30

Литература дополнительная

1.  , Теория вероятностей и прикладная статистика, ч.1. М.: Юнити, 2001.

2.  SPSS: искусство обработки информации. СПб.: ДиаСофтЮП, 2005.

3.  Методы социологического исследования. / . – 4-е изд. – М.: КДУ, 2006.

4.  SPSS 19: профессиональный статистический анализ данных. – СПб.: Питер, 2011.

5.  Анализ социологических данных. М.: Научный мир, 2000

6.  Статистика для всех. / Пер. с англ. , , . – М.: ДМК Пресс, 2015.

7.  Bluman A. Elementary statistics. McGraw-Hill, 2008.

Тема 11. Данные и переменные. Описательная статистика (меры среднего и меры разброса для разных типов шкал) и статистические графики.

Шкалы измерений (интервальная, порядковая, категориальная). Средние величины, медиана, мода. Дисперсия. Распределения и их характеристики. Статистическая визуализация. График плотности распределения. Диаграммы рассеяния. Гистограммы. Столбиковые диаграммы. Линейные диаграммы. Коробчатые диаграммы. Круговые диаграммы.

Литература основная

1.  Математико-статистические модели в социологии. М.: ИД ГУ-ВШЭ, 2007. С.19-70.

2.  Анализ социологических данных с помощью пакета SPSS : учебное пособие для вузов. – М.: Изд. дом ГУ ВШЭ, 2007, С.10-36.

3.  Теория вероятностей и математическая статистика для социологов и менеджеров: учебник для студентов учреждений высш. образования / Науч. ред.: . М. : Издательский центр «Академия», 2014. С.29-76.

4.  , Анализ данных на компьютере: учебное пособие. – М.: ИД «ФОРУМ», 2008. – С. 44-58.

5.  Маркетинговые исследования с SPSS: Учебное пособие. – М.: ИНФРА-М, 2007. – С.42-60.

6.  Agresti, A. and Finlay, B. Statistical Methods for the Social Sciences. 4th ed. Pearson Prentice Hall, 2009. Pp.31-72.

Литература дополнительная

1.  , Теория вероятностей и прикладная статистика, ч.1. М.: Юнити, 2001.

2.  SPSS: искусство обработки информации. СПб.: ДиаСофтЮП, 2005.

3.  Методы социологического исследования. / . – 4-е изд. – М.: КДУ, 2006.

4.  SPSS 19: профессиональный статистический анализ данных. – СПб.: Питер, 2011.

5.  Анализ социологических данных. М.: Научный мир, 2000

6.  Статистика для всех. / Пер. с англ. , , . – М.: ДМК Пресс, 2015.

7.  Bluman A. Elementary statistics. McGraw-Hill, 2008.

Тема 12. Точечное и интервальное оценивание. Доверительные интервалы для среднего и доли. Размер выборки.

Два вида оценивания: точечное и интервальное. Понятие стандартной ошибки. Доверительные интервалы для среднего арифметического и для доли. Уровень доверительной вероятности, его содержательный смысл. Связь точности исследования и объема выборки исследования.

Литература основная

1.  Математико-статистические модели в социологии. М.: ИД ГУ-ВШЭ, 2007. С.71-100.

2.  Анализ социологических данных с помощью пакета SPSS : учебное пособие для вузов. – М.: Изд. дом ГУ ВШЭ, 2007. – С.37-39

3.  Теория вероятностей и математическая статистика для социологов и менеджеров: учебник для студентов учреждений высш. образования / Науч. ред.: . М. : Издательский центр «Академия», 2014. С.124-176.

7.  Математическая статистика для социологов: задачник: учебное пособие для вузов / отв. ред. . – М.: Изд. дом ГУ-ВШЭ, 2010, С.45-65

4.  , Анализ данных на компьютере: учебное пособие. – М.: ИД «ФОРУМ», 2008. – С.125-146.

5.  Маркетинговые исследования с SPSS: Учебное пособие. – М.: ИНФРА-М, 2007. – С.42-60.

6.  Основы формирования выборки: лекции для студентов направления 040100.62 (Социология) – М.: ГУ-ВШЭ, 2005, С. 8-38.

7.  Agresti, A. and Finlay, B. Statistical Methods for the Social Sciences. 4th ed. Pearson Prentice Hall, 2009. Pp.73-142.

Литература дополнительная

1.  , Теория вероятностей и прикладная статистика, ч.1. М.: Юнити, 2001.

2.  SPSS: искусство обработки информации. СПб.: ДиаСофтЮП, 2005.

3.  Методы социологического исследования. / . – 4-е изд. – М.: КДУ, 2006.

4.  SPSS 19: профессиональный статистический анализ данных. – СПб.: Питер, 2011.

5.  Анализ социологических данных. М.: Научный мир, 2000

6.  Статистика для всех. / Пер. с англ. , , . – М.: ДМК Пресс, 2015.

7.  Bluman A. Elementary statistics. McGraw-Hill, 2008.

Тема 13. Статистические гипотезы и их проверка. Основные понятия и алгоритмы. Статистическая значимость.

Введение в проверку статистических гипотез. Базовые понятия: статистическая гипотеза, нулевая гипотеза, альтернативная гипотеза, направленные и ненаправленные альтернативные гипотезы, статистика критерия, фиксированный уровень значимости, минимальный уровень значимости (p-value), критическая область, ошибки 1 и 2 рода, статистический вывод и мн. др.

Примеры.

Литература основная

1.  Математико-статистические модели в социологии. М.: ИД ГУ-ВШЭ, 2007. С.101-107, 120-122, 130-140.

2.  Теория вероятностей и математическая статистика для социологов и менеджеров: учебник для студентов учреждений высш. образования / Науч. ред.: . М. : Издательский центр «Академия», 2014. С.177-197.

3.  Математическая статистика для социологов: задачник: учебное пособие для вузов / отв. ред. . – М.: Изд. дом ГУ-ВШЭ, 2010, С.66-68, 106-108

4.  , Анализ данных на компьютере: учебное пособие. – М.: ИД «ФОРУМ», 2008. – С.82-96.

5.  Agresti, A. and Finlay, B. Statistical Methods for the Social Sciences. 4th ed. Pearson Prentice Hall, 2009. Pp.143-147.

Литература дополнительная

1.  , Теория вероятностей и прикладная статистика, ч.1. М.: Юнити, 2001.

2.  Статистика для всех. / Пер. с англ. , , . – М.: ДМК Пресс, 2015.

3.  Bluman A. Elementary statistics. McGraw-Hill, 2008.

Тема 14. Совместное распределение переменных. Таблицы сопряженности. Критерий Хи-квадрат. Анализ стандартизированных остатков.

Понятие о двумерной частотной таблице и способах отражения в ее виде независимости рассматриваемых признаков. Ожидаемые частоты и наблюдаемые частоты.

Логика проверки гипотезы об отсутствии связи между двумя номинальными (или рассматриваемыми как номинальные) признаками на основе критерия Хи-квадрат. Основная модель. Интерпретация остатков. Примеры.

Литература основная

1.  Анализ социологических данных с помощью пакета SPSS: учебное пособие для вузов. – М.: Изд. дом ГУ ВШЭ, 2007. – С.57-67, 81.

2.  , Анализ данных на компьютере: учебное пособие. – М.: ИД «ФОРУМ», 2008. – С.240-253, 263-267.

3.  Теория вероятностей и математическая статистика для социологов и менеджеров: учебник для студентов учреждений высш. образования / Науч. ред.: . М. : Издательский центр «Академия», 2014. С.197-215.

4.  Маркетинговые исследования с SPSS: Учебное пособие. – М.: ИНФРА-М, 2007. – С.74-80.

5.  Agresti, A. and Finlay, B. Statistical Methods for the Social Sciences. 4th ed. Pearson Prentice Hall, 2009. Pp.221-255.

Литература дополнительная

1.  , Теория вероятностей и прикладная статистика, ч.1. М.: Юнити, 2001.

2.  SPSS: искусство обработки информации. СПб.: ДиаСофтЮП, 2005.

3.  SPSS 19: профессиональный статистический анализ данных. – СПб.: Питер, 2011.

4.  Статистика для всех. / Пер. с англ. , , . – М.: ДМК Пресс, 2015.

5.  Agresti, A. and Finlay, B. Statistical Methods for the Social Sciences. 4th ed. Pearson Prentice Hall, 2009

6.  Bluman A. Elementary statistics. McGraw-Hill, 2008.

Тема 15. Парные коэффициенты корреляции

Коэффициента линейной корреляции Пирсона (для переменных, измеренных на уровне шкал высокого порядка), коэффициенты ранговой корреляции Спирмена и Кендалла (для переменных, измеренных на порядковом уровне). Проверка статистических гипотез о равенстве коэффициентов 0. Соотнесение с ограничениями социологических шкал.

Литература основная

1.  Математико-статистические модели в социологии. М.: ИД ГУ-ВШЭ, 2007. С.126-127, 128-129.

2.  Теория вероятностей и математическая статистика для социологов и менеджеров: учебник для студентов учреждений высш. образования / Науч. ред.: . М. : Издательский центр «Академия», 2014. С.77-107, 264-287.

3.  Анализ социологических данных с помощью пакета SPSS: учебное пособие для вузов. – М.: Изд. дом ГУ ВШЭ, 2007. – С.67-81, 115-146, 166-182.

4.  Математическая статистика для социологов: задачник: учебное пособие для вузов / отв. ред. . – М.: Изд. дом ГУ-ВШЭ, 2010, С.34-44, 102-104.

5.  , Анализ данных на компьютере: учебное пособие. – М.: ИД «ФОРУМ», 2008. – С.253-263, 267-269, 208-219, 230-239.

6.  Маркетинговые исследования с SPSS: Учебное пособие. – М.: ИНФРА-М, 2007. – С.104-127.

7.  Agresti, A. and Finlay, B. Statistical Methods for the Social Sciences. 4th ed. Pearson Prentice Hall, 2009. Pp.255-300.

Литература дополнительная

1.  , Теория вероятностей и прикладная статистика, ч.1. М.: Юнити, 2001.

2.  SPSS: искусство обработки информации. СПб.: ДиаСофтЮП, 2005.

3.  SPSS 19: профессиональный статистический анализ данных. – СПб.: Питер, 2011.

4.  Статистика для всех. / Пер. с англ. , , . – М.: ДМК Пресс, 2015.

5.  Bluman A. Elementary statistics. McGraw-Hill, 2008.

Тема 16. Проверка гипотезы о математических ожиданиях (средних). Т-тест (одновыборочный). Гипотеза о равенстве доли определенному числу.

Алгоритм (правила) проверки гипотез. Статистический критерий проверки гипотез о равенстве математического ожидания и доли определенному числу (константе). Статистический критерий проверки гипотезы о равенстве двух математических ожиданий для случая парных (связных) выборок. Содержательный характер исследовательских задач. Примеры.

Литература основная

1.  Теория вероятностей и математическая статистика для социологов и менеджеров: учебник для студентов учреждений высш. образования / Науч. ред.: . М. : Издательский центр «Академия», 2014. С.226-228.

2.  Анализ социологических данных с помощью пакета SPSS : учебное пособие для вузов. – М.: Изд. дом ГУ ВШЭ, 2007. – С.94-96

3.  , Анализ данных на компьютере: учебное пособие. – М.: ИД «ФОРУМ», 2008. – С.147-158.

4.  Agresti, A. and Finlay, B. Statistical Methods for the Social Sciences. 4th ed. Pearson Prentice Hall, 2009. Pp.147-159.

Литература дополнительная

1.  , Теория вероятностей и прикладная статистика, ч.1. М.: Юнити, 2001.

2.  Статистика для всех. / Пер. с англ. , , . – М.: ДМК Пресс, 2015.

3.  Bluman A. Elementary statistics. McGraw-Hill, 2008.

Тема 17. Гипотеза о равенстве дисперсий в двух группах. Т-тест для двух независимых выборок. Т-тест для двух связных выборок. Гипотеза о равенстве долей в двух группах.

Алгоритм (правила) проверки гипотез. Статистический критерий проверки гипотезы о равенстве двух математических ожиданий для случая независимых выборок. Статистические критерии проверки гипотез о равенстве дисперсий и долей в двух группах. Содержательный характер исследовательских задач. Примеры.

Литература основная

1.  Математико-статистические модели в социологии. М.: ИД ГУ-ВШЭ, 2007. С.113-119.

2.  Теория вероятностей и математическая статистика для социологов и менеджеров: учебник для студентов учреждений высш. образования / Науч. ред.: . М. : Издательский центр «Академия», 2014. С.215-263.

3.  Анализ социологических данных с помощью пакета SPSS : учебное пособие для вузов. – М.: Изд. дом ГУ ВШЭ, 2007. – С.82-94, 97-99.

4.  Математическая статистика для социологов: задачник: учебное пособие для вузов / отв. ред. . – М.: Изд. дом ГУ-ВШЭ, 2010, С.79-105

5.  , Анализ данных на компьютере: учебное пособие. – М.: ИД «ФОРУМ», 2008. – С.158-169.

6.  Маркетинговые исследования с SPSS: Учебное пособие. – М.: ИНФРА-М, 2007. – С.81-90.

7.  Agresti, A. and Finlay, B. Statistical Methods for the Social Sciences. 4th ed. Pearson Prentice Hall, 2009. Pp.183-187, 191-197.

Литература дополнительная

1.  , Теория вероятностей и прикладная статистика, ч.1. М.: Юнити, 2001.

2.  SPSS: искусство обработки информации. СПб.: ДиаСофтЮП, 2005.

3.  SPSS 19: профессиональный статистический анализ данных. – СПб.: Питер, 2011.

4.  Статистика для всех. / Пер. с англ. , , . – М.: ДМК Пресс, 2015.

5.  Bluman A. Elementary statistics. McGraw-Hill, 2008.

Тема 18. Дисперсионный анализ (ANOVA).

Дисперсионный анализ как проверка статистической гипотезы о равенстве средних (формулировка гипотезы, используемый критерий, логика проверки). Однофакторный дисперсионный анализ. Основная модель. Класс решаемых задач. Понимание причинно-следственной связи при использовании однофакторного дисперсионного анализа (априорная модель такой связи). Примеры.

Литература основная

1.  Анализ социологических данных с помощью пакета SPSS : учебное пособие для вузов. – М.: Изд. дом ГУ ВШЭ, 2007. – С.99-114.

2.  Математико-статистические модели в социологии. М.: ИД ГУ-ВШЭ, 2007. С.144-190.

3.  Математическая статистика для социологов: задачник: учебное пособие для вузов / отв. ред. . – М.: Изд. дом ГУ-ВШЭ, 2010, С.113-124, 126-135

4.  , Анализ данных на компьютере: учебное пособие. – М.: ИД «ФОРУМ», 2008. – С.170-193.

5.  Маркетинговые исследования с SPSS: Учебное пособие. – М.: ИНФРА-М, 2007. – С.90-103.

6.  Agresti, A. and Finlay, B. Statistical Methods for the Social Sciences. 4th ed. Pearson Prentice Hall, 2009. Pp.369-376.

Литература дополнительная

1.  , Теория вероятностей и прикладная статистика, ч.1. М.: Юнити, 2001.

2.  SPSS: искусство обработки информации. СПб.: ДиаСофтЮП, 2005.

3.  SPSS 19: профессиональный статистический анализ данных. – СПб.: Питер, 2011.

4.  Статистика для всех. / Пер. с англ. , , . – М.: ДМК Пресс, 2015.

5.  Bluman A. Elementary statistics. McGraw-Hill, 2008.

  Образовательные технологии

Занятия проводятся в форме лекций и семинаров (в компьютерном классе).

  Оценочные средства для текущего контроля и аттестации студента

Тематика заданий текущего контроля

В 1 и 2 модулях студентам предлагаются две контрольные работы по задачам теории вероятностей и математической статистики, которые выполняются в классе.

В течение всего учебного года студентам предлагаются дополнительные задания, выполняемые по желанию (добровольно) в виде «Тренировочных задач» для самоподготовки (самопроверки) дома к каждой изученной теме курса. Эти задания требуют решения (расчетов) «вручную» или на компьютере (в программе SPSS). Тренировочные задачи обычно включают в себя самостоятельное решение и содержательную интерпретацию результатов анализа.

  Порядок формирования оценок по дисциплине

Аттестация знаний осуществляется в 10-балльной шкале.

Итоговая оценка за курс вычисляется следующим образом:

=

Перед вычислением итоговой оценки: накопленная оценка (отражающая успешность академической работы в течение 1-2 модулей) и оценка за экзамен (отражающая успешность выполнения письменной работы в конце 2-го модуля) округляются до целого. Округление производится в сторону ближайшего целого (арифметический способ).

Формами текущего контроля по данному курсу являются: 1 контрольная работа в первом модуле (она состоит из двух частей, распределенных во времени, – микро-контрольная А и микро-контрольная Б), 1 контрольная работа во втором модуле (она состоит из двух частей, распределенных во времени, – микро-контрольная А и микро-контрольная Б). Обе контрольные работы оцениваются в 10-балльной шкале.

Формами итогового контроля выступают: письменный экзамен (который проводится в конце 1 модуля) по материалам теории вероятностей и письменный экзамен (который проводится в конце 2 модуля) по матемариалам всего курса целиком с преимущественным акцентом на математическую статистику.

Оценка за первую часть дисциплины («Теория вероятностей», 1 модуль) формируется следующим образом:

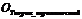= 0,6* + 0,2* + 0,2* , где

·  - оценка за письменную экзаменационную работу в 1-ом модуле (с весом 60%)

·  - оценка за контрольную работу в 1-ом модуле (с весом 20%).

·  - оценка за активную работу на семинарских занятиях (решение задач у доски), выполнение домашних заданий для самоподготовки и тренировки к каждому семинару по изученной теме в 1-ом модуле (с весом 20%).

Оценка за вторую часть дисциплины («Математическая статистика», 2 модуль) фор-

мируется следующим образом:

= 0,8*+0,2*, где

·  - оценка за контрольную работу во 2-ом модуле (с весом 80%).

·  - оценка за активную работу на семинарских занятиях (решение задач у доски), выполнение домашних заданий для самоподготовки и тренировки к каждому семинару по изученной теме в 1-ом и 2-ом модулях (с весом 20%).

Важные примечания.

В случае болезни или отсутствия на контрольной работе по уважительной причине, студенту нужно предупредить преподавателя, проводящего контрольную работу, до ее начала. Повторное проведение контрольных работ для студентов, пропустивших их по уважительной причине (подтвержденной соответствующими документами), назначается преподавателем, проводящим семинарские занятия. В случае пропуска контрольной работы по неуважительной причине и/или отсутствия соответствующих документов повторное проведение контрольной работы не производится.

Пересдача элементов текущего контроля (контрольных работ) не производится.

При округлении накопленной и итоговой оценок за курс «Теория вероятностей и математическая статистика» производится в соответствии с арифетическим правилом округлении. Так, например, оценка 3,5 балла округляется до 4.

  Учебно-методическое и информационное обеспечение дисциплины

  Базовые учебники

1.  , , Теория вероятностей: учебник для экономических и гуманитарных специальностей. М.: МЦНМО, 2009.

2.  , Анализ данных на компьютере: учебное пособие. – М.: ИД «ФОРУМ», 2008.

3.  Математико-статистические модели в социологии. М.: ИД ГУ-ВШЭ, 2007.

4.  Анализ социологических данных с помощью пакета SPSS: учебное пособие для вузов. – М.: Изд. дом ГУ ВШЭ, 2007.

5.  Теория вероятностей и математическая статистика для социологов и менеджеров: учебник для студентов учреждений высш. образования / Науч. ред.: . М. : Издательский центр «Академия», 2014.

6.  Agresti, A. and Finlay, B. Statistical Methods for the Social Sciences. 4th ed. Pearson Prentice Hall, 2009.

  Основная литература

1.  Томас Дж. Вероятность. М.: МЦНМО, 2015.

2.  Математическая статистика для социологов: задачник: учебное пособие для вузов / отв. ред. . – М.: Изд. дом ГУ-ВШЭ, 2010

3.  Маркетинговые исследования с SPSS: Учебное пособие. – М.: ИНФРА-М, 2007.

  Дополнительная литература

1.  , Теория вероятностей и прикладная статистика, ч.1. М.: Юнити, 2001.

2.  SPSS: искусство обработки информации. СПб.: ДиаСофтЮП, 2005.

3.  Методы социологического исследования. / . – 4-е изд. – М.: КДУ, 2006.

4.  SPSS 19: профессиональный статистический анализ данных. – СПб.: Питер, 2011.

5.  Практическая бизнес-статистика. М.: Издательский дом «Вильямс», 2004

6.  Анализ социологических данных. М.: Научный мир, 2000

7.  Хили Дж. Статистика. Социологические и маркетинговые исследования. СПб.: Питер, 2005

8.  Основы формирования выборки: лекции для студентов направления 040100.62 (Социология) – М.: ГУ-ВШЭ, 2005

9.  Статистика для всех. / Пер. с англ. , , . – М.: ДМК Пресс, 2015.

10.  Bluman A. Elementary statistics. McGraw-Hill, 2008.

  Программные средства

Для успешного освоения дисциплины студент использует следующие программные средства: SPSS.

  Дистанционная поддержка дисципли

Материалы к курсу, включающие в себя программу, слайды к лекциям и материалы к семинарам и практическим занятиям, домашние задания и базы данных, доступны в системе LMS.

11.  Материально-техническое обеспечение дисциплины

На лекциях, семинарах и практических занятиях используется проектор. Практические занятия проводятся в компьютерном классе с установленной на компьютерах программой SPSS.