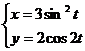МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования «МАТИ» - Российский государственный технологический университет им.
Кафедра «ТИАС»
КУРСОВАЯ РАБОТА
По курсу: «Теоретическая механика»
Группа: 2АСУ-2ДБ-074
Выполнил: .
Проверил:
Москва 2006
СОДЕРЖАНИЕ
1. Задание №1...................................................................................................... 3
1. Задание №2...................................................................................................... 6
2. Задание №3...................................................................................................... 9
3. Задание №4.................................................................................................... 11
Задание №1
Кинематика движения материальной точки
Вариант 29
Дано:
|
1. Определим максимальные и минимальные значения, которые могут принимать x и y из условия ограниченности функций синуса и косинуса
![]() ;
;
![]() ;
;
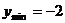
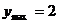
Значит:
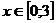
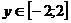
2. Выразим зависимость координаты y от координаты x
![]()
![]()
![]()
3. Положение точки при заданных параметрах
![]() ;
;
![]() .
.
4. Скорость точки при заданных параметрах
![]() ;
;
![]() ;
;
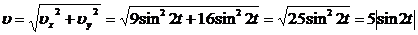 ;
;
 ;
;
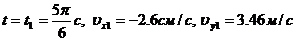 ;
;
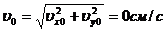 ;
;
![]() .
.
5. Ускорение точки при заданных параметрах
![]() ;
;
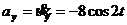 ;
;
![]() ;
;
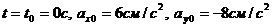 ;
;
![]() ;
;
- 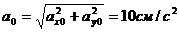 ;
;
![]() .
.
6. Касательное ускорение точки при заданных параметрах
![]() ;
;
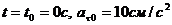 ;
;
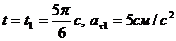 .
.
6. Нормальное ускорение точки при заданных параметрах
![]() ;
;
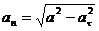 ;
;
![]() ;
;
![]() .
.
7. Радиус кривизны траектории в данной точке при заданных параметрах
![]() ;
;
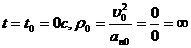 ;
;
![]() .
.
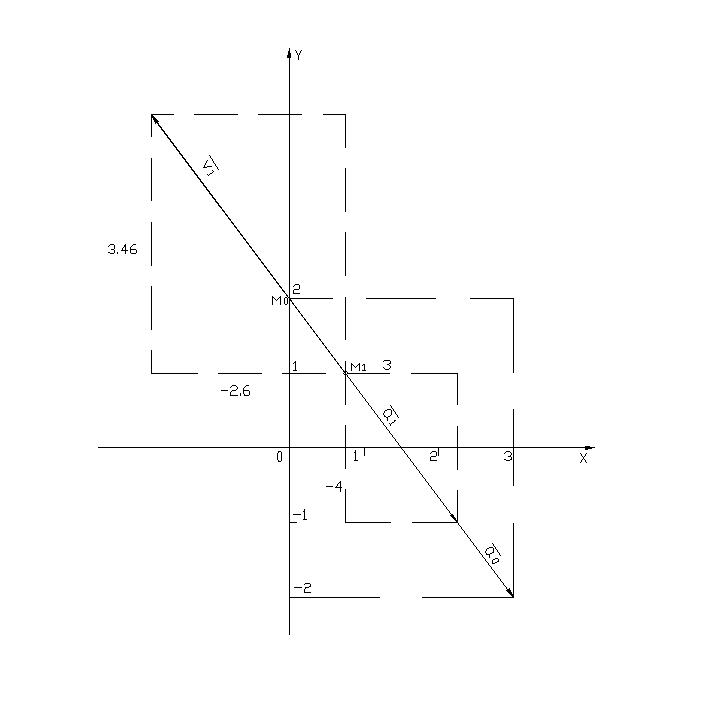
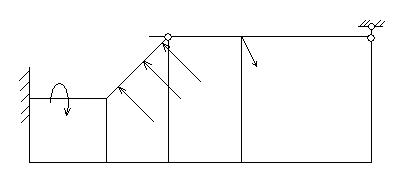
Рис.1. Чертеж к заданию №1
Задание №2
Сложное движение точки
Вариант 48
Дано:
|
1. Положение точки М:
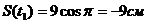 ;
;
2. Найдем абсолютную скорость:
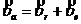 ;
;
![]() ;
;
![]() ;
;
![]() , где
, где 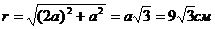 ;
;
![]() ;
;
![]() ;
;
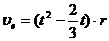 ;
;
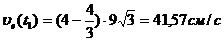 ;
;
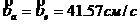 .
.
3. Найдем абсолютное ускорение:
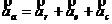 ;
;
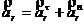 ;
;
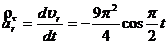 ;
;
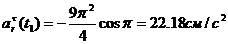 ;
;
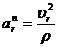 ;
; ![]()
![]() ;
;
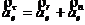 ;
;
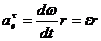 ;
;
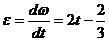 ;
;
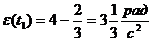 ;
;
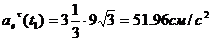
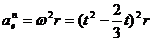 ;
;
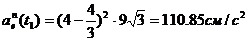
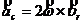 ;
;
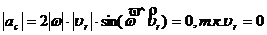 ;
;
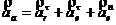 ;
;
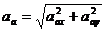
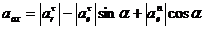 где
где 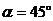 ;
;
 ;
;
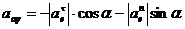 ;
;
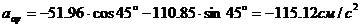 ;
;
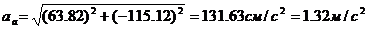 .
.
Ответ: ![]() ,
, ![]() .
.
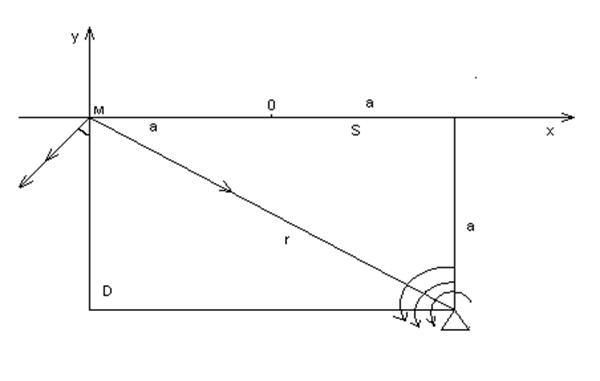
Рис.2. Чертеж к заданию №2
Задание №3
Статика
Вариант 154
Дано:
|
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Схема I
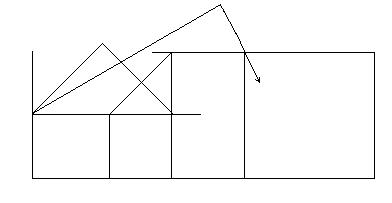
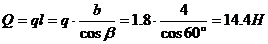 ;
;
Схема II
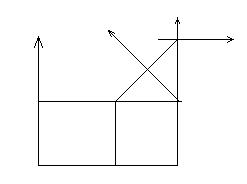 |
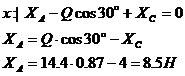
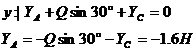
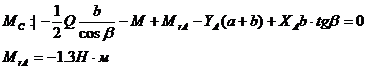
Схема III
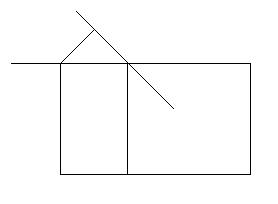
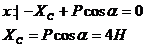
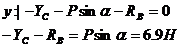
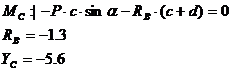
|
|
|
|
|
|
8.5 | -1.6 | -1.3 | 4 | -1.3 | -5.6 |
Проверка:
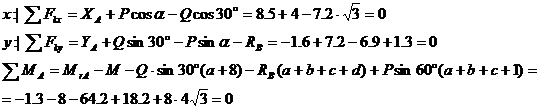
Задание №4
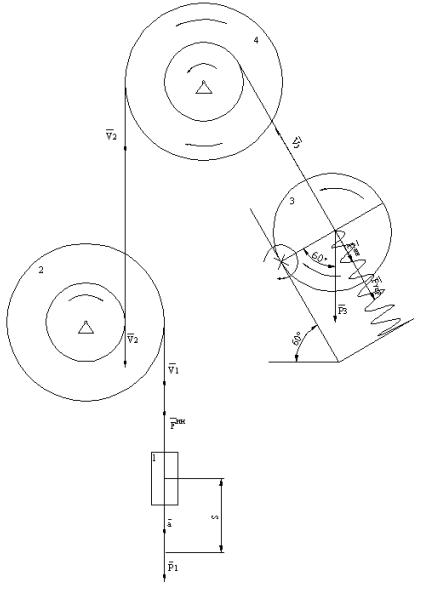 |
|
По теореме об изменении кинетической энергии:
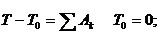
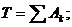
![]()
![]() ;
;
![]() , где
, где ![]() ;
;
![]() , где
, где ![]() ;
;
![]() , где
, где ![]() .
.
Кинематический анализ
![]() ;
;
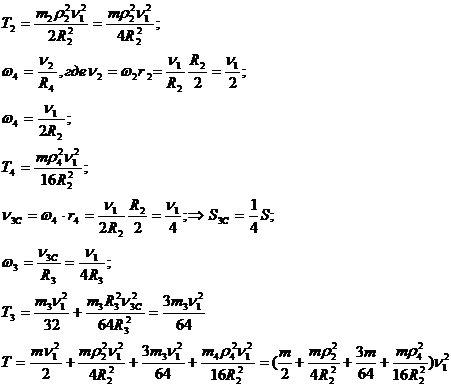
Расчет работы системы
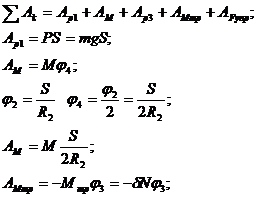
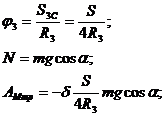
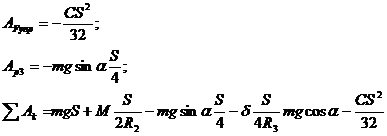
![]() Дж
Дж
![]()
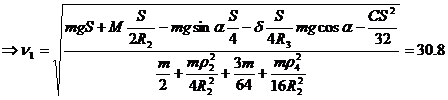 м/с
м/с
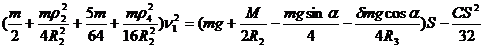
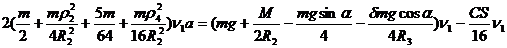
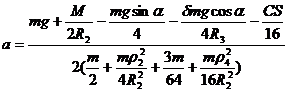
![]()
Метод Д’Аламбера-Лагранжа
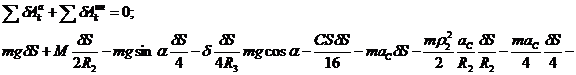
![]()
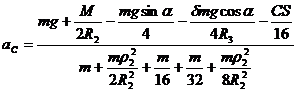
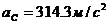 .
.
Найдем силы натяжения нитей.
По II закону Ньютона:
![]() ;
;
![]() ;
;
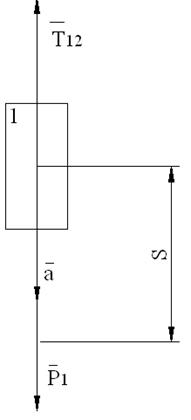
![]() ;
;
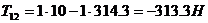 ;
;
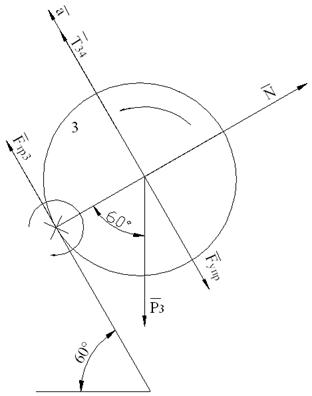
По II закону Ньютона:
![]()
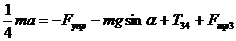
![]()
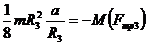
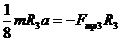
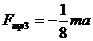
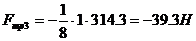
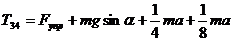
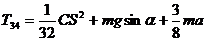
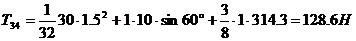 .
.