Задача № 1
по разделу «Теоретическая механика»
Стальная стержневая конструкция находится под действием сил, моментов и распределенной нагрузки.
Определить реакции опор твердого тела.
В этой группе задач исходные данные принимаются, в соответствии с шифром, следующим образом:
1. По последней цифре шифра принять схему нагружения.
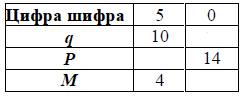
2. По первой цифре шифра из табл. 2 принять величину силы P.
3. По второй цифре шифра из табл. 2 принять величину распределенной нагрузки q.
4. По третьей цифре шифра из табл. 2 принять величину моментаM.
Таблица 2
Исходные данные к задаче № 1
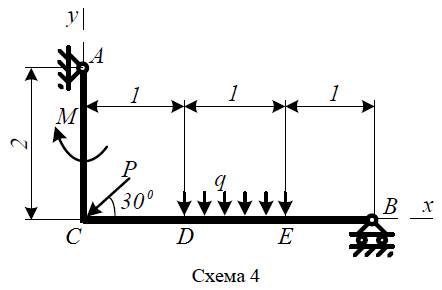
Задача № 2
по разделу «Теоретическая механика»
Определить для заданного положения скорости всех точек механизма и угловые скорости звеньев с помощью плана скоростей. Сделать проверку найденных значений с помощью мгновенных центров скоростей.
В этой группе задач исходные данные принимаются, в соответствии с шифром, следующим образом:
1. По последней цифре шифра принять схему рычажного механизма.
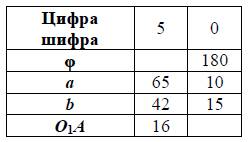
2. По первой цифре шифра из табл. 3 принять величину угла φ.
3. По второй цифре шифра из табл. 3 принять длину кривошипа O1A.
4. Недостающими длинами звеньев задаться самостоятельно.
Таблица 3
Исходные данные к задаче № 2
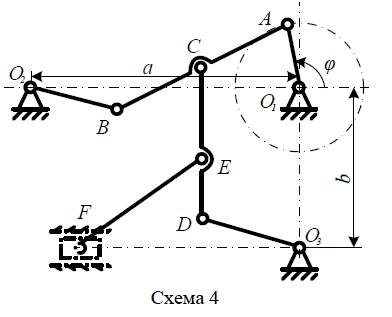
Задача № 3
по разделу «Сопротивление материалов»
Стальной стержень находится под действием продольных сил.
Построить эпюры внутренних продольных сил F и нормальных напряжений s, найти перемещение Dl сечения I–I. Влиянием собственного веса стержня пренебречь.
Модуль упругости стали Ест равен 215000 МПа.
В этой группе задач исходные данные принимаются, в соответствии с шифром, следующим образом:
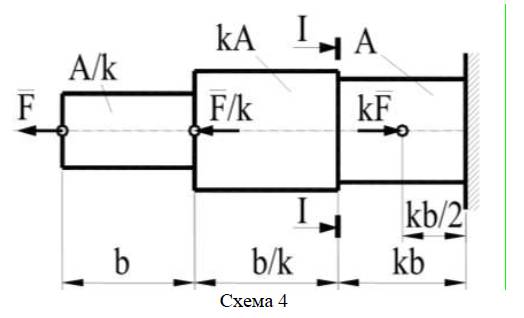
1. По последней цифре шифра принять схему нагружения.
2. По первой цифре шифра из табл. 4 принять величину силы F.
3. По второй цифре шифра из табл. 4 принять величину площади сечения А.
4. По третьей цифре шифра из табл. 4 принять величину коэффициента k.
5. По четвертой цифре шифра из табл. 4 принять величину, характеризующую длину стержня – b.
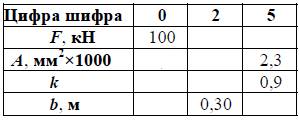
Таблица 4
Исходные данные к задаче № 3
На схемах 0–9 центрами маленьких окружностей обозначены точки
приложения сил.
Задача № 4
по разделу «Сопротивление материалов»
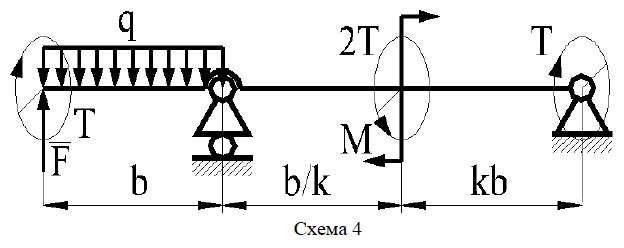
Для заданной схемы стальной балки круглого постоянного сечения,
нагруженной распределенной нагрузкой q, сосредоточенной силой F,
изгибающим моментом М и крутящими моментами Т, произвести следующие расчеты:
– определить составляющие реакций в опорах;
– построить эпюру поперечных сил;
– построить эпюру изгибающих моментов;
– построить эпюру крутящих моментов;
– пользуясь построенными эпюрами и механическими характери-
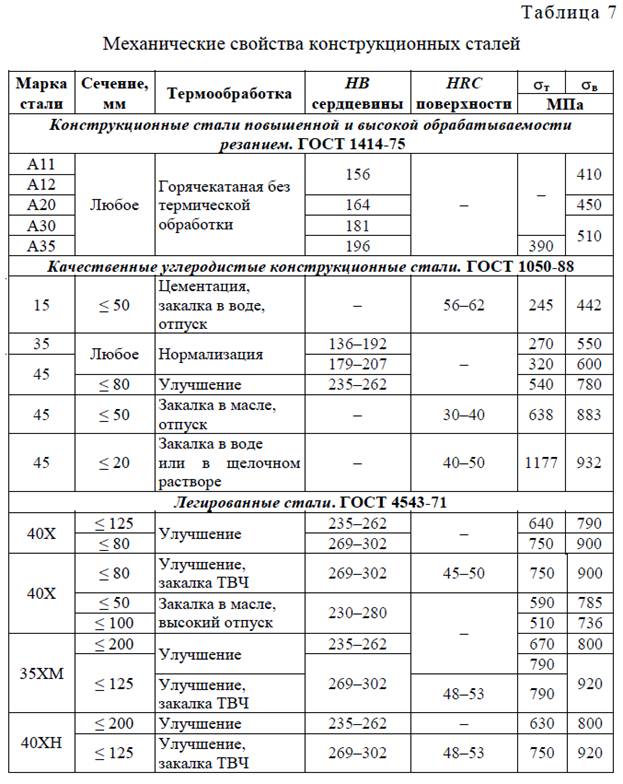
стиками принятого материала (табл. 7), по одной из теорий прочности
определить величину минимально допускаемого диаметра (полученное значение округлить до ближайшей большей величины из ряда нормальных линейных размеров по ГОСТ 6636-69 (табл. 6).
Маркой стали балки задаться самостоятельно (табл. 7).
Коэффициент безопасности по пределу текучести Sтp принять равным 2.
Исходные данные для решения задачи принять в соответствии со своим личным шифром (см. раздел 4) в следующем порядке:
1. По последней цифре шифра принять схему нагружения балки.
2. По первой цифре шифра из табл. 5 принять величину интенсивности распределенной нагрузки q.
3. По второй цифре шифра из табл. 5 принять величину силы F.
4. По третьей цифре шифра из табл. 5 принять величину изгибающего момента М.
5. По четвертой цифре шифра из табл. 5 принять величину, характеризующую длину балки – b.
6. По абсолютной величине разности первой и второй цифр шифра из табл. 5 принять величину крутящего момента Т.
7. По абсолютной величине разности первой и третьей цифр шифра из табл. 5 принять величину коэффициента k.
Таблица 5
Исходные данные к задаче № 4

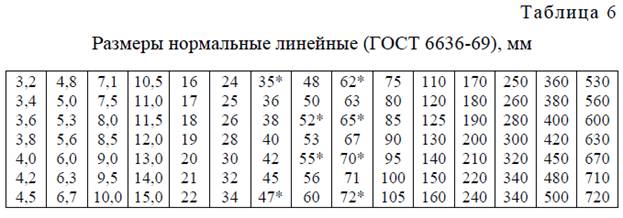
Примечание. В табл. 6 звездочкой (*) помечены размеры посадочных мест
для подшипников качения. В других случаях их использование не рекомендуется.
Указания:
Расчет балки круглого сечения на статическую прочность сводится к определению напряжений и к определению коэффициента безопасности и сравнению полученных значений с допускаемыми.
Напряжения в наиболее опасном сечении вала определяют (по третьей теории прочности) по формуле
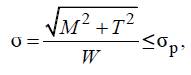
где М – максимальный изгибающий момент;
T – крутящий момент;
W – момент сопротивления.
Значения момента сопротивления для балки круглого сечения
![]()
Допускаемые напряжения σр равны:
![]()
где σт – предел текучести материала вала; значения σт приведены
в табл. 5;
Sтр – допускаемый коэффициент безопасности по пределу текучести;
Sтр =1,5¼2,0.
Коэффициент безопасности по пределу текучести определяется по
нижеприведенной формуле и его величина сравнивается с допускаемой
величиной:
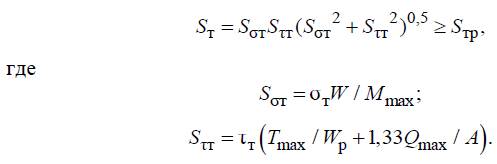
Здесь Mmax – наибольшее значение изгибающего момента в рассматри-
ваемом сечении;
Tmax – наибольшее значение крутящего момента в рассматривае-
мом сечении;
Qmax – наибольшее значение перерезывающей силы в рассчиты-
ваемом сечении;
σт , τт – предел текучести материала вала по нормальным и каса-
тельным напряжениям (табл. 5);
A – площадь рассматриваемого сечения.




