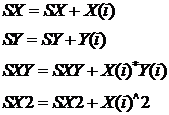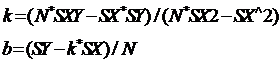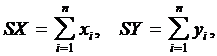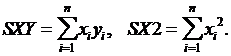Рис. 10.8

 

ввод данных

да

нет

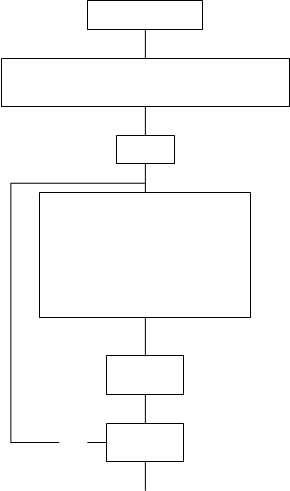
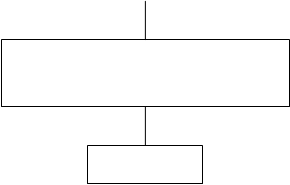
печать

Рис.10.9

Значения параметров k, b линейной функции находятся из системы вида 10.4. Блок-схема расчета параметров линейной регрессии приведена на рисунке 10.9.

В блок-схеме используются следующие обозначения:

Замечание: приведенная блок-схема позволяет рассчитать лишь значения параметров линейной регрессии, но не дает величины средней квадратичной ошибки (блок-схему для расчета величины читателю предлагаем составить самостоятельно).

Проделав необходимые вычисления, получаем:

Т. е. приближающее линейное уравнение запишется в виде

Для нахождения параметров c и m степенной функции воспользуемся формулой (10.7). Составив соответствующую программу для ЭВМ, получим:

Таким образом, уравнение степенной регрессии имеет вид

Как видно, сумма квадратов абсолютных погрешностей для линейной функции составляет , для степенной функции — Видно, что приближение в виде степенной функции в данном случае предпочтительнее.

Для решения задачи приближения функции методом наименьших квадратов сформулируем основные шаги алгоритма.

1. Ввод исходных данных.

2. Выбор вида уравнения регрессии.

3. Преобразование данных к линейному типу зависимости.

4. Получение параметров уравнения регрессии.

5. Обратное преобразование данных и вычисление суммы квадратов

отклонений вычисленных значений функции от заданных.

1. Вывод результатов.

10.5 Контрольные вопросы

1. В чем суть приближения таблично заданной функции по методу

наименьших квадратов? Чем отличается этот метод от метода интерполяции?

2. Каким образом сводится задача построения приближающих функций в виде различных элементарных функций к случаю линейной функции?

3. В чем состоит основная идея метода наименьших квадратов?

4. Почему используется принцип минимума суммы квадратов абсолютных величин, а не суммы самих абсолютных величин? Ответ обосновать и подтвердить примерами.

5. Почему метод наименьших квадратов наиболее эффективен, если функция f(x) линейна относительно искомых параметров?

10.6 Задания к лабораторной работе № 10

1. Методом наименьших квадратов вывести формулы для параметров и и приближающей квадратичной функции:

2. Построить точечный график по заданной таблице варианты заданий указаны в таблице 10.8). Подобрать наиболее подходящие по внешнему виду приближающие функции. После нахождения значений параметров каждой из приближающих функций найти суммы квадратов абсолютных значений по формуле (10.2) и по их значениям установить, какое из приближений лучше. На том же чертеже построить графики рассчитанных приближающих функций.

В оформленной работе должны быть приведены все графики, составленные алгоритмы или блок-схемы, тексты программ и результаты расчетов, ответы на контрольные вопросы.

Таблица 10.8

Вариант

Результаты опыта

1

x

0,0

0,5

1,0

11,5

2,0

2,5

y

-13,65

-5,77

-0,07

6,95

12,05

18,97

x

3,0

3,5

4,0

4,5

5,0

5,5

y

25,67

31,57

38,44

46,20

51,33

58,83

2

x

0,0

0,5

1,0

1,5

2,0

2,5

y

15,65

183,47

2226,27

27121,09

330398

4025059

3

x

0,0

0,5

1,0

1,5

2,0

2,5

y

10,652

10,730

10,074

10,455

10,951

10,532

x

3,0

3,5

4,0

4,5

5,0

5,5

y

10,310

10,934

10,564

10,703

10,667

10,334

4

x

-4,0

-3,5

-3,0

-2,5

-2,0

-1,5

y

7,49

6,95

5,95

5,93

5,42

4,99

x

-1,0

-0,5

0,0

0,5

1,0

1,5

y

4,45

3,90

3,85

2,91

2,41

1,40

5

x

0

1

2

3

4

5

y

0,129

x

6

7

8

9

10

y

6

x

-5,0

-4,5

-4,0

-3,5

-3,0

-2,5

y

54,98

45,52

37,00

29,53

23,00

17,53

x

-2,0

-1,5

-1,0

-0,5

0

0,5

y

12,97

9,49

7,034

5,50

4,98

5,32

7

x

10

12

14

16

18

20

y

29,5885

29,5880

29,6747

29,6869

29,7484

29,7223

x

22

24

26

28

30

32

y

29,7710

29,8260

29,8100

29,8038

29,8554

29,8885

8

x

1,0

1,2

1,4

1,6

1,8

2,0

y

3,875

3,640

3,475

3,363

3,260

3,195

x

2,2

2,4

y

3,125

3,072

9

x

0,2

0,4

0,6

0,8

1,0

1,2

y

2,617

1,893

1,659

1,347

1,888

1,698

x

1,4

1,6

y

1,323

1,127

10

x

-5,0

-4,1

-3,2

-2,3

-1,4

-0,5

y

-45,03

-35,99

-27,04

-18,00

-8,99

-0,01

x

0,4

y

8,98

11

x

1,0

1,2

1,4

1,6

1,8

2,0

y

9,35

8,48

7,74

7,30

6,84

6,61

x

2,2

2,4

y

6,28

6,13

12

x

0,9

1,1

1,3

1,5

1,7

1,9

y

8,48

7,23

6,35

5,71

5,22

4,84

x

2,1

2,3

y

4,52

4,26

13

x

0,4

0,7

1,0

1,3

1,6

1,9

y

8,481

5,382

4,153

3,480

3,069

2,777

x

2,2

2,5

y

2,571

2,418

14

x

2

3

4

5

6

7

y

8,15

13,45

22,17

36,55

60,26

99,35

x

8

9

10

11

12

y

163,79

270,05

445,24

734,08

1210,286

15

x

2

3

4

5

6

7

y

0,967

1,346

1,872

2,604

3,621

5,037

x

8

9

10

11

12

y

7,010

9,75

13,56

18,86

26,24

16

x

2

3

4

5

6

7

y

37,52

22,76

13,80

8,37

5,08

3,08

x

8

9

10

11

12

y

1,87

1,13

0,68

0,41

0,25

17

x

2

3

4

5

6

7

y

12,21

13,498

14,918

16,487

18,220

20,137

x

8

9

10

11

12

y

22,255

24,596

27,183

30,040

33,200

18

x

2

3

4

5

6

7

y

0,967

1,346

1,872

2,604

3,621

5,037

x

8

9

10

11

12

y

7,010

9,75

13,56

18,86

26

24

19

x

0

1

2

3

4

5

y

0

2,0

2,297

2,491

2,639

2,759

x

6

7

8

9

10

11

y

2,861

2,95511

3,031

3,104

3,169

3,231

20

x

0

1

2

3

4

5

y

0

10,00

14,114

17,32

20,00

22,36

x

6

7

8

9

10

11

y

24,49

26,45

28,28

30,00

31,62

33,16

21

x

1

2

3

4

5

6

y

1,0

0,707

0,577

0,500

0,447

0,408

x

7

8

9

10

11

12

y

0,377

0,353

0,333

0,316

0,301

0,288

22

x

1

2

3

4

5

6

y

10

9,33

8,95

8,70

8,51

8,36

x

7

8

9

10

11

12

y

8,23

8,12

8,03

7,94

7,86

7,80

23

x

1

2

3

4

5

6

y

-2,00

-3,38

-4,19

-4,77

-5,22

-5,58

x

7

8

9

10

11

112

y

-5,89

-6,16

-6,39

-6,60

-6,79

-6,96

24

x

1

2

3

4

5

6

y

5,50

5,25

5,16

5,112

5,10

5,08

x

7

8

9

10

11

12

y

5,07

5,07

5,05

5,05

5,04

5,04

25

x

1

2

3

4

5

6

y

0,17

0,25

0,30

0,33

0,36

0,37

x

7

8

9

10

11

12

y

0,39

0,40

0,41

0,42

0,42

0,43

Из за большого объема этот материал размещен на нескольких страницах:
1 2