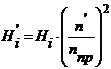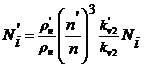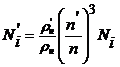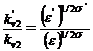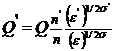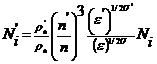![]() , (4)
, (4)
где h – величина шага для аргумента ![]() функции
функции ![]() .
.
Основу моделирования режима работы компрессорной машины (КМ) составляет математическое описание её характеристики, точность описания которой определяет точность оценки энергопотребления ГПА. Математическая модель характеристик КМ включает в себя аппроксимацию фактических данных и методику их пересчёта на иные условия работы (Tн, состав газа, n).
Для моделирования ГДХ ЦБК в газовой промышленности получил широкое распространение метод приведённых характеристик. Основу модели составляют зависимости ![]() ,
, 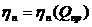 , полученные для одной (базовой) частоты вращения ротора ЦБК (
, полученные для одной (базовой) частоты вращения ротора ЦБК (![]() ). Для аппроксимации используют полиномы вида
). Для аппроксимации используют полиномы вида ![]() ;
; ![]() , где
, где ![]() – коэффициенты полиномов, m – степень полинома. Точность аппроксимации в соответствии с методом наименьших квадратов обеспечивается выбором степени полинома m, исходя из минимума среднеквадратичного отклонения расчётных и фактических значений. Пересчёт на иные условия работы осуществляется по уравнениям (5), которые являются частным случаем общих уравнений теории подобия лопаточных машин (таблица 1).
– коэффициенты полиномов, m – степень полинома. Точность аппроксимации в соответствии с методом наименьших квадратов обеспечивается выбором степени полинома m, исходя из минимума среднеквадратичного отклонения расчётных и фактических значений. Пересчёт на иные условия работы осуществляется по уравнениям (5), которые являются частным случаем общих уравнений теории подобия лопаточных машин (таблица 1).
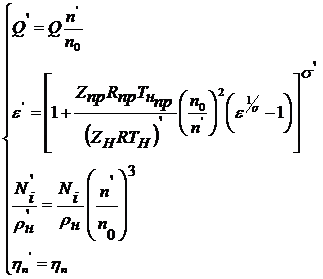 , (5)
, (5)
где 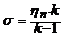 ,
, ![]() ;
; ![]() – плотность (кг/м3) газа на входе в компрессор;
– плотность (кг/м3) газа на входе в компрессор; ![]() – внутренняя мощность ЦБК (кВт, МВт). Индексом пр обозначены параметры приведения ГДХ, штрихом ‑ параметры пересчёта на «новые» условия работы.
– внутренняя мощность ЦБК (кВт, МВт). Индексом пр обозначены параметры приведения ГДХ, штрихом ‑ параметры пересчёта на «новые» условия работы.
Таблица 1 – Формулы расчёта ГДХ ЦБК при изменении условий его работы
№ п/п | Допущения | Расчётные зависимости | |||
Производитель-ность | удельная работа (напор) | Политроп-ный КПД | Внутренняя мощность ЦБК | ||
1 | Общий вид |
|
|
|
|
2 |
(при |
|
| ||
3 |
|
|
| ||
|
Известно, что зависимости метода приведённых характеристик (таблица 1, строка 2) верны в случае ε < 1,5, а допущение о равенстве КПД (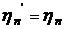 ) выполняется приближённо, и только для одно - и двухступенчатых ЦБК. Погрешность пересчёта увеличивается с ростом ε, отклонением от условий подобия по числам Маха и Рейнольдса, показателю адиабаты (Re = idem, Mu = idem, k=idem), а также от области автомодельности (Re > 1∙106, Mu < 0,6).
) выполняется приближённо, и только для одно - и двухступенчатых ЦБК. Погрешность пересчёта увеличивается с ростом ε, отклонением от условий подобия по числам Маха и Рейнольдса, показателю адиабаты (Re = idem, Mu = idem, k=idem), а также от области автомодельности (Re > 1∙106, Mu < 0,6).
При моделировании высоконапорных многоступенчатых ЦБК необходимо учитывать изменения ![]() (таблица 1, строка 1) и
(таблица 1, строка 1) и ![]() . Аналитические зависимости для определения данных параметров отсутствуют, существующие расчётные методы (вычислительная газовая динамика, использование характеристик модельных ступеней) характеризуются сложностью и трудоёмкостью, требуют большого количества исходных данных и, в основном, используются разработчиками КМ.
. Аналитические зависимости для определения данных параметров отсутствуют, существующие расчётные методы (вычислительная газовая динамика, использование характеристик модельных ступеней) характеризуются сложностью и трудоёмкостью, требуют большого количества исходных данных и, в основном, используются разработчиками КМ.
Эмпирические зависимости имеют ограниченную область применения, например формулы для ![]() (таблицы 1, строка 3) могут применяться только для одноступенчатых ЦБК. Поэтому наиболее надёжным способом определения вида ГДХ многоступенчатых ЦБК является проведение испытаний при различных частотах вращения. Экспериментальные данные удобно аппроксимировать двухпараметрическими уравнениями:
(таблицы 1, строка 3) могут применяться только для одноступенчатых ЦБК. Поэтому наиболее надёжным способом определения вида ГДХ многоступенчатых ЦБК является проведение испытаний при различных частотах вращения. Экспериментальные данные удобно аппроксимировать двухпараметрическими уравнениями:
![]() , (6)
, (6)
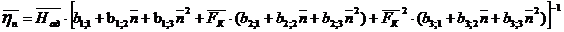 , (7)
, (7)
где ![]() ‑ относительная частота вращения ротора компрессора;
‑ относительная частота вращения ротора компрессора; 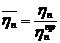 ‑ относительный политропный КПД;
‑ относительный политропный КПД; 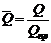 ‑ безразмерная производительность;
‑ безразмерная производительность; 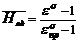 ‑ безразмерный напор;
‑ безразмерный напор; 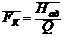 ‑ параметр, учитывающий фактическое изменение параметров ГДХ с изменением
‑ параметр, учитывающий фактическое изменение параметров ГДХ с изменением ![]() .
.
Значения коэффициентов ![]() и
и ![]() определяются в результате решения системы линейных уравнений, в качестве исходных данных используются значения экспериментальных параметров ГДХ для трёх различных частот вращения ротора ЦБК. В случае изменения параметров
определяются в результате решения системы линейных уравнений, в качестве исходных данных используются значения экспериментальных параметров ГДХ для трёх различных частот вращения ротора ЦБК. В случае изменения параметров 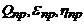 значения коэффициентов
значения коэффициентов ![]() и
и ![]() в (6) и (7) определяются по формулам вида:
в (6) и (7) определяются по формулам вида:
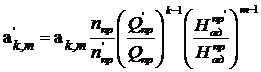 (8)
(8)
В третьей главе проведена оценка методической погрешности метода МО (ММО), влияния компонентного состава газа и выбора уравнения состояния на результаты расчёта показателей энергоэффективности, а также сравнительный анализ способов моделирования ГДХ ЦБК, рассмотренных в главе 2.
Методическая погрешность ММО обусловлена допущением ![]() при проведении линеаризации точных зависимостей. Из сравнения результатов расчёта
при проведении линеаризации точных зависимостей. Из сравнения результатов расчёта ![]() и
и ![]() по точным формулам и формулам в виде МО (2) следует, что погрешность определения
по точным формулам и формулам в виде МО (2) следует, что погрешность определения ![]() по уравнениям в виде МО всегда меньше величины отклонения параметров работы ГПА. Погрешность расчёта
по уравнениям в виде МО всегда меньше величины отклонения параметров работы ГПА. Погрешность расчёта ![]() не превышает 1,0 % при изменении удельной мощности
не превышает 1,0 % при изменении удельной мощности ![]() = ±20,0 % и
= ±20,0 % и ![]() от минус 15,0 % до плюс 7,0 % Таким образом, точность уравнений в виде МО удовлетворяет целям данного исследования.
от минус 15,0 % до плюс 7,0 % Таким образом, точность уравнений в виде МО удовлетворяет целям данного исследования.
Определено, что выбор уравнения состояния не оказывает существенного влияния на точность расчётов по ММО, вследствие малой величины коэффициентов влияния ![]() (0,10-0,15) и
(0,10-0,15) и ![]() (10∙10-5-16∙10-5). Указанные значения получены в результате расчётов с использованием расчётной процедуры НТП МГ (Нормы технологического проектирования МГ), уравнений Пенга-Робинсона, Бенедикта-Вэбба-Рабина, Соаве-Редлиха-Квонга.
(10∙10-5-16∙10-5). Указанные значения получены в результате расчётов с использованием расчётной процедуры НТП МГ (Нормы технологического проектирования МГ), уравнений Пенга-Робинсона, Бенедикта-Вэбба-Рабина, Соаве-Редлиха-Квонга.
Сравнительный анализ точности методик пересчёта ГДХ с учётом изменения ![]() (таблица 1, строка 3) и без него (метод приведённых характеристик) проведён с использованием данных о характеристиках ЦБК различного назначения, напорности и конструктивного исполнения, опубликованных в литературе (таблица 2), и фактических режимов работы ЦБК в составе ГПА ДКС (СПЧ /1,7).
(таблица 1, строка 3) и без него (метод приведённых характеристик) проведён с использованием данных о характеристиках ЦБК различного назначения, напорности и конструктивного исполнения, опубликованных в литературе (таблица 2), и фактических режимов работы ЦБК в составе ГПА ДКС (СПЧ /1,7).
Определялись максимальная величина погрешности ![]() и
и ![]() , и их влияние на расчёт показателей энергоэффективности ГПА,
, и их влияние на расчёт показателей энергоэффективности ГПА, ![]() и
и ![]() (рисунок 2). Также учитывалась погрешность определения расхода на границе помпажа.
(рисунок 2). Также учитывалась погрешность определения расхода на границе помпажа.
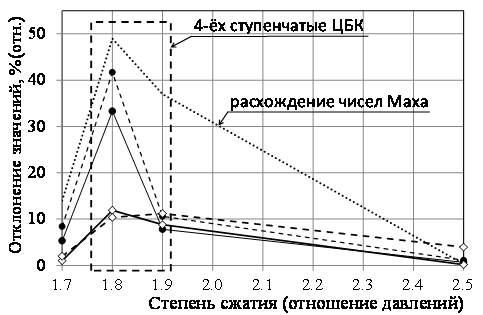
а) |
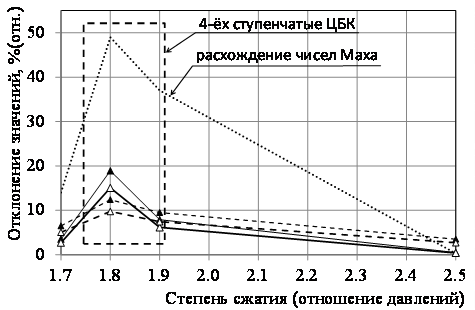
б) |
Рисунок 2 – Погрешность определения параметров работы ГПА для различных методик пересчёта ГДХ ЦБК: а) Погрешность определения б) Погрешность определения мощности |
● – политропный КПД; ◊ ‑ степень сжатия; ▲― мощность «на валу» привода; ∆ ‑ расход топливного газа |
Значения ![]() и
и ![]() на рисунке 2б определялись по формулам:
на рисунке 2б определялись по формулам:
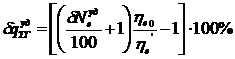 , (9)
, (9)
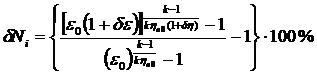 , (10)
, (10)
где 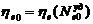 ,
, ![]() ;
; ![]() ,
, ![]() определялись для загрузки мощности привода Kз=0,9.
определялись для загрузки мощности привода Kз=0,9.
Таблица 2 – Компрессоры для сравнения методик моделирования ГДХ
№ п/п | Название | Тип компрессора | Количество рабочих колёс | Номинальная степень сжатия | Объект применения |
1* | СПЧ /1,7 | ЦБК (НЛСМ в составе ГПА) | 3 | 1,7 | ГПА-16ДКС-07 в составе ДКС |
2 | ‑ | ЦБК | 1 | 2,5 | Холодильная установка |
3 | двухкорпусный ЦБК 95-81-1 | Секция низкого давления (ЦНД) | 4 | 1,9 | Газоперерабатывающий завод |
4 | Секция высокого давления (ЦВД) | 4 | 1,8 | ||
*‑ фактические данные |
Сравнительный анализ точности способов моделирования ГДХ проведён на примере характеристики одноступенчатого ЦБК с εном= 4,0 (рисунок 3).

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 |