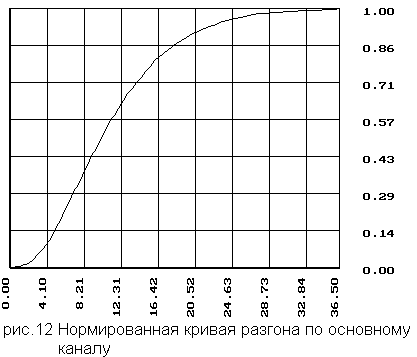
4.3 Нормированная кривая разгона по основному каналу
табл. 4.3
1 | 0,0000 | 0,0000 | 30 | 14,5000 | 0,7579 |
2 | 0,5000 | 0,0050 | 31 | 15,0000 | 0,7779 |
3 | 1,0000 | 0,0100 | 32 | 15,5000 | 0,7977 |
4 | 1,5000 | 0,0166 | 33 | 16,0000 | 0,8143 |
5 | 2,0000 | 0,0315 | 34 | 16,5000 | 0,8259 |
6 | 2,5000 | 0,0498 | 35 | 17,0000 | 0,8408 |
7 | 3,0000 | 0,0713 | 36 | 17,5000 | 0,8541 |
8 | 3,5000 | 0,0896 | 37 | 18,0000 | 0,8673 |
9 | 4,0000 | 0,1177 | 38 | 18,5000 | 0,8756 |
10 | 4,5000 | 0,1493 | 39 | 19,0000 | 0,8872 |
11 | 5,0000 | 0,1824 | 40 | 19,5000 | 0,8988 |
12 | 5,5000 | 0,2189 | 41 | 20,0000 | 0,9088 |
13 | 6,0000 | 0,2554 | 42 | 20,5000 | 0,9154 |
14 | 6,5000 | 0,2919 | 43 | 21,0000 | 0,9221 |
15 | 7,0000 | 0,3201 | 44 | 21,5000 | 0,9287 |
16 | 7,5000 | 0,3566 | 45 | 22,0000 | 0,9353 |
17 | 8,0000 | 0,3947 | 46 | 22,5000 | 0,9420 |
18 | 8,5000 | 0,4312 | 47 | 23,0000 | 0,9486 |
19 | 9,0000 | 0,4594 | 48 | 23,5000 | 0,9552 |
20 | 9,5000 | 0,4942 | 49 | 24,0000 | 0,9602 |
21 | 10,0000 | 0,5290 | 50 | 24,5000 | 0,9652 |
22 | 10,5000 | 0,5622 | 51 | 25,5000 | 0,9701 |
23 | 11,0000 | 0,5857 | 52 | 25,5000 | 0,9751 |
24 | 11,5000 | 0,6153 | 53 | 26,0000 | 0,9801 |
25 | 12,0000 | 0,6434 | 54 | 26,5000 | 0,9851 |
26 | 12,5000 | 0,6716 | 55 | 27,0000 | 0,9900 |
27 | 13,0000 | 0,6899 | 56 | 27,5000 | 0,9950 |
28 | 13,5000 | 0,7131 | 57 | 28,0000 | 1,0000 |
29 | 14,0000 | 0,7347 |
5. Аппроксимация методом Симою.
С помощью программы ASR в пункту аппроксимации последовательно считаем площади каждой из кривой разгона для последующего получения уравнения передаточной функции.
Для кривой разгона по внешнему контуру для объекта второго порядка получаем следующие данные:
Значения площадей:
F1= 6.5614
F2= 11.4658
F3= -4.5969
F4= -1.1636
F5= 44.0285
F6= -120.0300
Ограничимся второй площадью. F1<F2, а F3 отрицательная. Следовательно для определения передаточной функции необходимо решить систему уравнений:
a1 = F1 + b1
a2 = F2 + b2 + b1 F2
a3 = F3 + b3 + b2 F1 + b1 F2
a1 = 6.5614 + b1
a2 = 11.4658 + b1 6.5614
0 = - 4.5969 + b1 11.4658
Решив систему получаем : b1 = 0.4
a1 = 6.9614
a2 = 14.0904
Тогда передаточная функция объекта второго порядка по внешнему контуру имеет вид:
0.4 s
W(s)=-------
2
14.0904 s + 6.9614 s + 1
Для кривой разгона по внутреннему контуру для объекта второго порядка получаем следующие данные:
Значения площадей:
F1= 9.5539
F2= 24.2986
F3= -16.7348
F4= -14.7318
F5= 329.7583
F6= -1179.3989
Для определения передаточной функции решаем систему, так как F3<0.
a1 = 9.5539 + b1
a2 = 24.2986 + 9.5539 b2
0 = -16.7348 + b1 24.2986
Решив систему получаем : b1 = 0.6887
a1 = 10.2426
a2 = 30.8783
Тогда передаточная функция объекта второго порядка по внутреннему контуру имеет вид:
0.6887 s + 1
W(s) = -------
2
30.8783s + 10.2426 s + 1
Для кривой разгона по заданию для объкта третьего порядка с запаздыванием получаем следующие данные:
Значения площадей:
F1= 10.6679
F2= 38.1160
F3= 30.4228
F4= -46.5445
F5= 168.8606
F6= -33.3020
Так как F3<F2 и положительна, то ограничиваемся второй площадью и передаточная объекта третьего порядка по управлению имеет вид:
1
W(s) =
2
38.1160 s + 10.6679 s + 1
6. Проверка аппроксимации методом Рунге - Кутта.
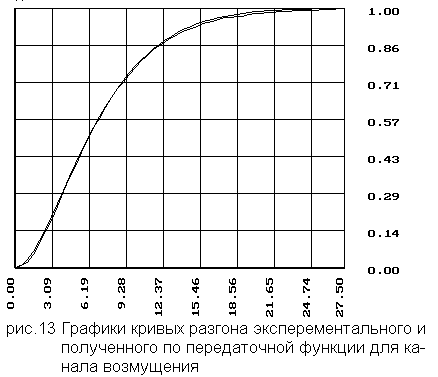
В программе ASR в пункте передаточная функция задаем полученные передаточные функции. И затем строим графики экспериментальной и аналитической кривых разгона (по полученной передаточной функции).
6.1 Для кривой разгона по внешнему контуру
Устанавливаем для проверки методом Рунге-Кутта конечное время 27c, шаг 0,5с.
6.2 Для кривой разгона по внутреннему контуру
Устанавливаем конечное время 39с, шаг 0,5с.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |




