по выполнению самостоятельной работы
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
 |
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Кафедра теоретической механики
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Методические указания
по выполнению самостоятельной работы
М о с к в а 2009
С о с т а в и т е л ь
доцент, кандидат технических наук
Компьютерная правка и верстка
Лицензия ЛР № 000 от 01.01.2001 г.

Подписано в печать 14.09.2009 г. Формат 60´84 1/16 Печать офсетная
И-149 Объем 2 п. л. Т. 2000 Заказ 498
 |
Московский государственный строительный университет.
Типография МГСУ. Москва, Ярославское ш., 26
КАФЕДРА ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
Теоретическая механика является одной из фундаментальных общенаучных дисциплин физико-математического цикла. На материале курса теоретической механики базируются такие важные для общего инженерного образования дисциплины, как сопротивление материалов, теория механизмов и машин, строительная механика, гидравлика, теория колебаний и др., а также большое число специальных инженерных дисциплин, посвящённых изучению движения различных механизмов, методов расчёта, сооружения и эксплуатации таких объектов, как мосты, тоннели, плотины, водоводы, гидромелиоративные сооружения, трубопроводы и многое другое. Изучение теоретической механики должно также дать тот минимум фундаментальных знаний, на базе которых будущий специалист сумеет самостоятельно овладеть всем новым, с чем ему придётся сталкиваться в ходе дальнейшего научно-технического прогресса. Наконец, изучение курса теоретической механики способствует расширению научного кругозора и повышению общей культуры будущего специалиста, развитию его мышления и становлению его мировоззрения.
Кафедра теоретической механики – одна из старейших кафедр нашего университета. Работает с момента основания МИСИ, являясь одной из основополагающих кафедр общенаучного цикла. В различные годы кафедру возглавляли известные специалисты в области механики – проф., д. т.н. , чл.-корр. АН УССР, проф., д. ф.-м. н. , проф., д. ф.-м. н. , проф., д. т.н. , проф., д. т.н. . В настоящее время кафедрой заведует проф., д. т.н. .
Большое число работников кафедры принимало активное участие в Великой Отечественной войне, как на полях сражений, так и в оборонной промышленности. Рядовыми воевали Юрий Петрович Алексеев и Олег Николаевич Савинов. Практически всю войну с 1941 по 1944 год прошли, обслуживая боевые самолёты, авиамеханики Иван Петрович Былинкин и Анатолий Петрович Грязнов. Анатолий Михайлович Морковкин с февраля 1942 по май 1945 года был артиллерийским разведчиком, закончив войну в Пруссии. Александр Николаевич Глаголев был лётчиком-истребителем, командиром звена. В войне с Японией участвовал Леонид Андреевич Ларионов. На преподавательской работе в военных учебных заведениях работали военные инженеры Лев Михайлович Лахтин, Василий Семёнович Медведев, Иван Акимович Скорик. Ведущими инженерами НИИ ВВС были во время войны Арсений Яковлевич Суханов и Леонид Агафонович Бойко. внёс большой вклад в разработку бронезащиты самолётов и совершенствование авиационного оружия. Все эти ветераны составляли костяк кафедры в 70-80-е годы.
Добрых слов заслуживают Степан Григорьевич Терзибашьянц и Людмила Владимировна Янковская, отдавшие МИСИ лучшие годы жизни. пришёл на кафедру в 1932 году и проработал на ней 55 лет. Помимо преподавательской вёл большую административную работу. Был и начальником учебной части института, и деканом факультета ТЭС. Более 55 лет отдала кафедре . Многие поколения специалистов строителей с благодарностью вспоминают этих замечательных преподавателей.
Весной 2009 г. кафедра торжественно отметила 100-летие доктора технических наук, профессора Бойко, который заведовал кафедрой с 1959 по 1980 г. Леонид Агафонович занимает особое место в истории кафедры, являясь по сути организатором того ядра преподавательского коллектива, который и сегодня во многом определяет лицо кафедры. Будучи крупным специалистом в области механики тел переменной массы, внёс значительный вклад в создание и совершенствование военной техники в военное и послевоенное время. После ВОВ работал консультантом ЦАГИ. Обладая незаурядным талантом чтения лекций, считал обучение и научное воспитание студентов одной из важнейших задач учёного. Многие известные в наши дни специалисты в свои студенческие и аспирантские года, а иногда и в зрелом возрасте внимательно слушали лекции Леонида Агафоновича, потому что знали – на этих лекциях они могут получить то, что не написано ни в одной книге.
В 1982 году заведывание кафедрой принял доктор технических наук, профессор Игорь Григорьевич Филиппов – крупный специалист в области динамических задач механики деформируемого твёрдого тела, теории колебаний упругих и вязкоупругих элементов строительных конструкций. Автор 250 научных работ и 11 монографий.
Кафедра всегда выделяла из своей среды сотрудников, занимавших достойное место в административном аппарате нашего института. Уже упоминался , долгие годы возглавлявший факультет ТЭС. работал директором НИИОУС, а затем возглавлял кафедру АСУ. Работают на кафедре или работали ранее нынешние декан МиАС , директор ИФО , заместитель директора ИФО , заведующий кафедрой инженерной геодезии , проректор МГСУ , первый проректор МГСУ .
На сегодняшний день кафедра представляет собой сложившийся коллектив научно-педагогических кадров. На кафедре работают 6 профессоров, 12 доцентов, 4 ассистента и 2 лаборанта.
На кафедре работает научно-педагогическая школа “Теория расчёта сооружений и элементов конструкций”, основанная академиком АН СССР . В настоящее время школу возглавляет Олег Олегович Егорычев, доктор технических наук, профессор, заведующий кафедрой теоретической механики МГСУ, первый проректор МГСУ. Научная деятельность школы развивается по следующим основным направлениям:
- теория колебаний упругих и вязкоупругих элементов строительных конструкций;
- динамическая теория устойчивости строительных конструкций;
- методы расчета многокомпонентных сред при нестационарных воздействиях;
- разработка методов сейсмо - и виброзащиты сооружений;
- анализ применимости численных методов решения динамических задач на основе сравнения с аналитическими решениями;
и ряд других направлений.
Сотрудники кафедры принимали и принимают участие в работе и организации многих российских и международных научных конференций. На регулярной основе издаются сборники научных трудов кафедры.
Кафедра вносит весомый вклад в подготовку специалистов высшей квалификации. За последние 20 лет аспирантами кафедры защищено более 40 диссертаций на соискание учёной степени кандидата технических наук. Подготовлено и защищено 11 диссертаций на соискание учёной степени доктора технических наук.
Сотрудники кафедры, обладая большим научным потенциалом и педагогическим опытом, в большинстве своём являются талантливыми преподавателями, профессионалами, знающими и любящими своё дело. Идёт постоянная работа по совершенствованию методики изложения курса. На кафедре работает научно-методический семинар, позволяющий ведущим преподавателям обменяться опытом, а молодым этот опыт приобрести. С целью обеспечения самостоятельной работы студентов проводится большая работа по созданию и совершенствованию учебной литературы. За последние годы подготовлено свыше 30 учебных пособий и большое количество методических работ.
Кафедра активно внедряет в учебный процесс современные формы преподавания. Разрабатываются компьютерные тесты по курсу теоретической механики для текущего контроля успеваемости, подготавливаются электронные учебные материалы для дистанционного обучения. Разработаны и внедрены в учебный процесс материалы мультимедийной иллюстрации лекций и практических занятий. Идёт работа над созданием электронного учебника.
Открытие новых специальностей в МГСУ потребовало разработки новых курсов. Разработан односеместровый курс теоретической механики для специальностей “Инженерная защита окружающей среды” и “Комплексное использование и охрана водных ресурсов”. Для студентов ИФО специальностей “Прикладная механика” и “Прикладная математика” разработаны новые курсы: “Введение в волновую механику”, “Аналитическая динамика и теория колебаний”; “Детали машин и основы конструирования”; “Проблемы динамики и прочности машин”; “История механики”,”История и методология науки в области прикладной механики”.
Сотрудники кафедры с уверенностью и надеждой смотрят в будущее, прекрасно осознавая роль и место кафедры в системе формирования и воспитания инженеров-строителей. Теоретическая механика, будучи важным инструментом в решении многих научных задач, является необходимой основой для изучения всех инженерных дисциплин и, видимо, единственной в МГСУ дисциплиной, прививающей навыки формализованной (математической) постановки задач, анализа систем и разработки расчётных схем, выбора способа решения и анализа полученных результатов.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ОРГАНИЗАЦИИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ
В качестве основной используется традиционная технология изучения материала, предполагающая живое общение преподавателя и студента. Существенным дополнением служат, разработанные на кафедре иллюстративные материалы. Для реализации программы мультимедийного сопровождения лекций и практических занятий используется аудитория, оборудованная проектором и экраном. Отдельные вопросы могут быть проиллюстрированы при помощи имеющегося комплекта демонстрационных приборов.
Каждый студент должен иметь в печатном виде учебные пособия, соответствующие читаемому курсу, или конспекты лекций. Предполагается создание электронных учебников и системы контроля текущей успеваемости, использующей компьютерные технологии.
Для успешного освоения теоретического и практического материала дисциплины «Теоретическая механика» обучающийся должен владеть знаниями и навыками, полученными при изучении курса высшей математики. Особенно важными для изучения курса теоретической механики являются такие разделы курса высшей математики, как векторная алгебра и аналитическая геометрия, дифференциальное и интегральное исчисления, дифференциальные уравнения (в т. ч. необходимо иметь общее представление о дифференциальных уравнениях в частных производных).
Изучение дисциплины подразумевает аудиторные занятия (лекции и практические занятия) и самостоятельную работу студентов.
Лекции содержат теоретическую основу курса. Практические занятия призваны обучить студента применять полученные теоретические знания для постановки и решения конкретных прикладных задач, а также привить навыки анализа полученных результатов. В условиях ограниченного времени, отводимого на аудиторные занятия, и в случае небольших по количеству слушателей потоков не имеет смысла чёткое разделение аудиторных занятий на лекции и практические занятия.
В процессе самостоятельной работы студент закрепляет полученные знания и навыки, выполняя расчетно-графические работы, включающие в себя материал определенного фрагмента курса.
Все виды деятельности студента должны быть обеспечены доступом к учебно-методическим материалам (учебникам, учебным пособиям, методическим указаниям к решению задач, методическими указаниями к выполнению расчетно-графических работ). Учебные материалы должны быть доступны в печатном виде, а кроме этого могут быть представлены в электронном варианте (электронный учебник, обучающая программа и. т.д.) и предоставляться на CD и/или размещаться на сайте учебного заведения.
Изучаемый курс разделен на тематические блоки, изучение которых заканчивается выполнением соответствующей расчетно-графической работы. Выполненная расчетно-графическая работа в указанные сроки передается преподавателю для проверки. Сданная работа проверяется, рецензируется и возвращается студенту. Возвращенная и, при необходимости, исправленная работа подлежит защите преподавателю. При защите работы студент должен продемонстрировать как знание теоретических вопросов данного блока, так и навык решения соответствующих задач.
Выполнение и защита расчетно-графической работы является формой промежуточного контроля знаний по данному блоку. При успешном прохождении промежуточного контроля по каждому из блоков, предусмотренных в данном семестре, студент получает зачет или допуск к экзамену. При наличии соответствующей материально-технической и проработанной методической базы, при промежуточном контроле, как один из элементов, может допускаться компьютерное тестирование.
В качестве итогового контроля предусмотрен экзамен. Студент должен изложить темы, предложенные в экзаменационном билете, решить задачу и ответить на дополнительные вопросы. Экзамен может проводиться как в устной, так и в письменной форме.
Приступая к изучению курса, студент должен ознакомиться с его программой и календарным графиком изучения курса и выполнения расчетно-графических работ.
План УЧЕБНЫХ ЗАНЯТИЙ
Содержание лекционного курса
Лекция 1. (Семестр 2)
Введение в механику. Предмет механики. Основные понятия механики – масса и сила. Системы отсчёта. Основные модели материальных тел, используемые в теоретической механике. Свободные и несвободные тела. Связи и их реакции. Основные понятия и определения статики – система сил, равнодействующая, эквивалентность систем сил. уравновешенная система сил. Основные аксиомы статики – действия над силами, приложенными в одной точке; действия над системами сил; силовой ноль. Действие силы на абсолютно твёрдое тело – силу можно переносить вдоль её линии действия в любую точку. Момент силы относительно точки и оси. Геометрический и аналитический способы вычисления момента силы относительно точки. Физический и геометрический смысл момента силы относительно точки.
Лекция 2. (Семестр 2)
Главный вектор и главный момент системы сил. Связь между главными моментами системы сил, вычисленными относительно двух различных точек. Пара сил. Плоскость действия и плечо пары сил Момент пары сил – определение и способ его вычисления. Теорема о параллельном переносе силы. Теорема о сложении пар сил, расположенных в пересекающихся плоскостях или в одной плоскости.
Лекция 3. (Семестр 2)
Основные теоремы статики. Теорема о приведении произвольной системы сил к одному центру. Приведение системы сил к двум силам. Необходимые и достаточные условия равновесия системы сил в векторной и координатной формах записи. Теорема об эквивалентности системы сил. Эквивалентность пар сил – момент полностью задаёт действие пары сил на абсолютно твёрдое тело.
Лекция 4. (Семестр 2)
Приведение системы сил к простейшему виду. Статические инварианты. Анализ возможных случаев приведения системы сил к простейшему виду – динамический винт, равнодействующая, пара сил, уравновешенная система сил.
Замечание: следующие темы носят, в основном, прикладной характер и подробно изучаются на практических занятиях.
Статический расчёт механических систем. Частные виды силовых систем. Система сходящихся сил. Система параллельных сил. Система сил, расположенных в одной плоскости. Система сочленённых тел. Расчёт ферм. Статически определимые и статически неопределимые конструкции.
Лекция 5. (Семестр 2)
Объёмные и поверхностные силы. Центр параллельных сил. Центр тяжести механической системы и сплошного тела. Определение положения центра тяжести однородного тела. Частные случаи – однородная пластина, однородный стержень. Методы определения положения центра тяжести – симметрия однородных тел, метод разбиений, метод отрицательных масс.
Лекция 6. (Семестр 2)
Распределённая нагрузка. Замена распределённой нагрузки равнодействующей. Частные случаи – равномерно и линейно распределённая нагрузка. Реакция негладкой поверхности. Сила трения при покое и при скольжении. Трение качения и верчения. Равновесие тел при наличии трения.
Лекция 7. (Семестр 2)
Кинематика точки. Основные понятия и задачи кинематики. Координатный способ задания движения точки. Радиус-вектор точки. Траектория точки и способы её построения. Скорость точки – определение и способ её вычисления при координатной форме задания движения. Ускорение точки – определение и способ его вычисления при координатной форме задания движения. Расположение вектора ускорения точки по отношению к траектории.
Лекция 8. (Семестр 2)
Естественный способ задания движения точки. Естественный трёхгранник. Вычисление скорости точки при естественном способе задания её движения. Вычисление ускорения точки при естественном способе задания её движения. Радиус кривизны траектории. Частные случаи движения точки – равнопеременное и равномерное движения.
Лекция 9. (Семестр 3)
Кинематика твёрдого тела. Основные задачи кинематики твёрдого тела. Поступательное движение твёрдого тела. Закон движения. Основные свойства. Вращение твёрдого тела вокруг неподвижной оси. Закон вращения. Распределение скоростей точек тела при вращательном движении (формула Эйлера). Распределение ускорений точек тела при вращении. Векторы угловой скорости и углового ускорения тела. Формула Эйлера в векторной форме. Осестремительное и вращательное ускорения точки.
Лекция 10. (Семестр 3)
Плоскопараллельное движение твёрдого тела. Закон движения. Распределение скоростей точек плоской фигуры. Мгновенный центр скоростей. Способы определения положения мгновенного центра скоростей и его использование для определения скоростей точек плоской фигуры. Распределение ускорений точек плоской фигуры. Способы определения ускорений точек плоской фигуры. Мгновенный центр ускорений. Способы определения положения мгновенного центра ускорений и его использование для определения ускорений точек плоской фигуры. Сферическое движение твёрдого тела. Углы Эйлера. Мгновенная угловая скорость и мгновенное угловое ускорение. Движение свободного твёрдого тела.
Лекция 11. (Семестр 3)
Сложное движение точки. Основные понятия и определения. Формулы Пуассона. Абсолютная и относительная производные вектора. Теорема сложения скоростей при сложном движении точки. Теорема сложения ускорений при сложном движении точки (теорема Кориолиса). Правило Жуковского.
Лекция 12. (Семестр 3)
Основные понятия. Модели материальных тел – материальная точка, механическая система, геометрически неизменяемая механическая система, абсолютно твёрдое тело. Основные законы механики (законы Ньютона). Дифференциальные уравнения движения материальной точки – в векторной форме и в проекциях на декартовы оси координат и на оси естественного трёхгранника. Первая основная задача динамики – постановка и метод решения. Вторая основная задача динамики – постановка и метод решения.
Лекция 13. (Семестр 3)
Линейные колебания материальной точки. Постановка задачи. Движение точки под действием восстанавливающей силы. Амплитуда, частота, период и фаза колебаний. Влияние постоянной силы на свободные незатухающие колебания. Движение точки при наличии сопротивления. Анализ возможных случаев.
Лекция 14. (Семестр 3)
Вынужденные колебания при отсутствии сопротивления. Резонанс. Вынужденные колебания при наличии сопротивления. Относительное движение точки. Дифференциальные уравнения относительного движения точки. Сила инерции материальной точки. Условия относительного покоя и относительного равномерного прямолинейного движения. Принцип относительности Галилея.
Лекция 15. (Семестр 4)
Возможные подходы к решению задачи об определении движения точек механической системы. Основные свойства внутренних сил. Количество движения материальной точки и механической системы. Теорема об изменении количества движения механической системы. Момент количества движения материальной точки и механической системы. Теорема об изменении кинетического момента механической системы в дифференциальной и интегральной формах. Центр масс механической системы. Способ вычисления количества движения механической системы. Теорема о движении центра масс. |
Лекция 16. (Семестр 4)
Кинетическая энергия материальной точки и механической системы. Вычисление кинетической энергии абсолютно твёрдого тела при поступательном, вращательном и плоскопараллельном движениях. Работа и мощность силы. Вычисление мощности и элементарной работы силы при различных способах задания движения точки приложения силы. Потенциальные силы. Потенциальная энергия механической системы. Теорема об изменении кинетической энергии механической системы в дифференциальной и интегральной формах. Закон сохранения полной механической энергии механической системы.
Лекция 17. (Семестр 4)
Система осей Кёнига. Первая и вторая теоремы Кёнига. Теорема об изменении кинетического момента относительно центра масс механической системы.
Лекция 18. (Семестр 4)
Кинетический момент твёрдого тела при сферическом движении твёрдого тела. Моменты инерции. Теорема Гюйгенса-Штейнера. Примеры вычисления осевых моментов инерции – сплошной однородный цилиндр, однородная труба, однородный стержень, однородная треугольная и прямоугольная пластины.
Лекция 19. (Семестр 4)
Вычисление кинетической энергии абсолютно твёрдого тела при поступательном, вращательном и плоскопараллельном движениях. Работа внутренних сил геометрически неизменяемой механической системы
Лекция 20. (Семестр 4)
Некоторые частные случаи вычисления работы силы – работа силы тяжести, работа упругой силы, работа вращающего момента. Дифференциальные уравнения поступательного движения твёрдого тела. Дифференциальное уравнение вращательного движения твёрдого тела. Дифференциальные уравнения плоскопараллельного движения твёрдого тела.
Лекция 21. (Семестр 4)
Принцип Даламбера. Сила инерции Даламбера. Основные уравнения кинетостатики. Главный вектор и главный момент сил инерции механической системы. Вычисление главного вектора и главного момента сил инерции абсолютно твёрдого тела при поступательном, вращательном и плоскопараллельном его движениях.
Лекция 22. (Семестр 4)
Классификация связей – связи удерживающие и неудерживающие, стационарные и нестационарные, голономные и неголономные. Возможные скорости и возможные перемещения. Идеальные связи. Примеры идеальных и неидеальных связей.
Лекция 23. (Семестр 4)
Принцип возможных перемещений. Примеры исследования равновесия механизмов. Применение принципа возможных перемещений для определения сил реакций идеальных связей. Использование принципа возможных перемещений при наличии неидеальных связей.
Лекция 24. (Семестр 4)
Общее уравнение динамики. Применение общего уравнения динамики к исследованию движения механической системы со многими степенями свободы. Принцип Даламбера-Лагранжа.
Лекция 25. (Семестр 4)
Обобщённые координаты и обобщённые силы. Уравнения Лагранжа 2-го рода. Применение уравнений Лагранжа 2-го рода к исследованию движения механической системы со многими степенями свободы.
Перечень практических занятий
Занятия Семестр 2)
Определение опорных реакций тела, нагруженного системой сил, расположенных в одной плоскости. Пара сил. Задачи из §§ 2, 3 и 4.
Занятие 4. (Семестр 2)
Жёсткая и скользящая заделки. Распределённая нагрузка. Задачи из §§ 3 и 4.
Занятия Семестр 2)
Определение опорных реакций системы тел, нагруженных системой сил, расположенных в одной плоскости. Задачи из §§ 3 и 4.
Занятие 7. (Семестр 2)
Расчёт ферм. Задачи из § 4.
Занятие 8. (Семестр 2)
Равновесие тела при наличии трения. Задачи из § 5.
Занятия Семестр 2)
Определение опорных реакций тела, нагруженного произвольной системой сил. Задачи из § 8.
Занятие 11. (Семестр 2)
Приведение системы сил к простейшему виду. Задачи из § 7.
Занятие 12. (Семестр 2)
Определение положения центра тяжести Задачи из § 9.
ЗанятияСеместр 2)
Определение основных кинематических характеристик точки при различных способах задания её движения. Задачи из §§ 10, 11 и 12.
Занятие 15. (Семестр 2)
Определение скоростей и ускорений точек тела, вращающегося вокруг неподвижной оси. Задачи из §§ 13 и 14.
Занятие 16. (Семестр 2)
Определение скоростей точек тела, совершающего плоскопараллельное движение.
Задачи из § 16.
Занятия 17 – 18. (Семестр 3)
Определение ускорений точек тела, совершающего плоскопараллельное движение.
Задачи из § 18.
Занятия 19 – 20. (Семестр 3)
Вычисление скорости и ускорения точки при её сложном движении. Задачи из §§ 22 и 23.
Занятия 21 – 23. (Семестр 3)
Две основные задачи динамики материальной точки. Задачи из §§ 26, 27 и 32.
Занятия 24 – 25. (Семестр 3)
Общие теоремы динамики. Задачи из §§ 35, 36, 38.
Занятия 26 – 28. (Семестр 4)
Движение абсолютно твёрдого тела. Задачи из §§ 35, 37, 39.
Занятия 29 – 30. (Семестр 4)
Принцип Даламбера. Задачи из §§ 41 и 42.
Занятия 31 – 34. (Семестр 4)
Элементы аналитической механики. Задачи из §§ 46, 47 и 48.
РАСЧЁТНО-ГРАФИЧЕСКИЕ РАБОТЫ
И КОНТРОЛЬНЫЕ ЗАДАНИЯ
КОМПЛЕКСНАЯ КОНТРОЛЬНАЯ РАБОТА № 1
ТЕМА: «Определение опорных реакций тела, нагруженного системой сил, расположенных в одной плоскости».
Контрольная работа или индивидуальная задача, выдаваемая для домашнего решения в недельный срок (на усмотрение преподавателя).
Срок проведения – четвёртая неделя второго семестра.
ТЕМА: «Расчёт ферм».
Контрольная работа или индивидуальная задача, выдаваемая для домашнего решения в недельный срок (на усмотрение преподавателя).
Срок проведения – восьмая неделя второго семестра.
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 1 на тему: «Приведение системы сил к простейшему виду».
Выдача – одиннадцатая неделя второго семестра; приём – четырнадцатая неделя второго семестра.
КОМПЛЕКСНАЯ КОНТРОЛЬНАЯ РАБОТА № 2
ТЕМА: «Определение основных кинематических характеристик точки при различных способах задания её движения».
Контрольная работа или индивидуальная задача, выдаваемая для домашнего решения в недельный срок (на усмотрение преподавателя).
Срок проведения – первая неделя третьего семестра.
ТЕМА: «Вычисление скорости и ускорения точки при её сложном движении».
Контрольная работа или индивидуальная задача, выдаваемая для домашнего решения в недельный срок (на усмотрение преподавателя).
Срок проведения – восьмая неделя третьего семестра.
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 2 на тему: «Кинематическое исследование плоского механизма ».
Выдача – пятая неделя третьего семестра; приём – четырнадцатая неделя третьего семестра.
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 3 на тему: «Динамическое исследование механических систем с одной и двумя степенями свободы с использованием общих теорем динамики и уравнений Лагранжа 2-го рода».
Выдача: часть 1 – четвёртая неделя четвёртого семестра; часть 2 – десятая неделя четвёртого семестра; часть 3 – четырнадцатая неделя четвёртого семестра; приём – пятнадцатая неделя четвёртого семестра.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Самостоятельная работа представляет собой важную составную часть учебного процесса, на которую отводится около половины учебных часов, предусмотренных рабочей программой изучения дисциплины. Самостоятельная работа включает в себя изучение лекций, как теоретической основы курса, выполнение задаваемых на дом практических задач, а также выполнение расчётно-графических работ и контрольных заданий.
Для успешного освоения теоретического и практического материала дисциплины «Теоретическая механика» обучающийся должен владеть знаниями и навыками, полученными при изучении курса высшей математики. Особенно важными для изучения курса теоретической механики являются такие разделы курса высшей математики, как векторная алгебра и аналитическая геометрия, дифференциальное и интегральное исчисления, дифференциальные уравнения (в т. ч. необходимо иметь общее представление о дифференциальных уравнениях в частных производных). Поэтому, осваивая курс теоретической механики, студент при необходимости должен обращаться к учебно-методической и справочной литературе по высшей математике.
Курс теоретической механики традиционно делится на три раздела – статика, кинематика и динамика. На изучение курса теоретической механики отводится три семестра – второй, третий и четвёртый. В качестве итогового контроля предусматривается экзамен по разделам статика и динамика и зачёт по разделу кинематика. В течение семестров студент должен выполнить расчётно-графические задания и контрольные задания, предусмотренные рабочей программой.
В самостоятельной работе студент должен использовать учебники по теоретической механике, перечень которых приведён в конце данной работы. Существенную помощь могут оказать учебные пособия, конспекты лекций и методические разработки кафедры теоретической механики МГСУ (см. библиографический список). В учебных пособиях изложен основной теоретический материал, приведено решение большого количества типовых задач по всем изучаемым темам и даны методические рекомендации к практическому использованию теоретического материала. Издаваемые кафедрой сборники задач содержат различные варианты расчётно-графических работ, контрольных задач и задач для самостоятельной проработки.
Ниже приводятся некоторые рекомендации, касающиеся основных подходов к освоению ключевых вопросов дисциплины. Эти рекомендации относятся в основном к разделу «Статика», поскольку именно в этом разделе закладывается фундамент методологии дисциплины.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО РАЗДЕЛУ «СТАТИКА»
Общий подход к решению задачи об определении реакций опор
Во многих случаях, встречающихся в инженерной практике, заранее известно, что некоторое тело находится в равновесии. Например, оно соответствующим образом закреплено (имеет опоры). На тело действуют заданные силы, которые называют активными. Природа активных сил, как правило, не указывается, т. е. неважно какие тела и по каким физическим законам взаимодействуют с рассматриваемым телом, дан только результат этого взаимодействия в виде сил. Под действием активной нагрузки тело оказывает давление на опоры (связи), со стороны которых, в соответствии с третьим законом Ньютона, возникают реакции связей. Задача состоит в определении сил реакций связей.
Сила реакции связи заранее неизвестна, она зависит от приложенных к телу активных сил и вида самой связи. Заранее можно только утверждать, что сила реакции связи направлена в сторону, противоположную той, куда данная связь не даёт перемещаться телу.
При решении задач об определении сил реакций опор предлагается следующая последовательность действий.
1. Выбрать тело (или систему тел), равновесие которого будет рассматриваться, и изобразить на чертеже приложенную к выбранному телу активную нагрузку.
2. Ввести реакции связей, изобразив силы реакций на чертеже. Если направление сил реакций заранее неизвестно, необходимо показать их составляющие.
3. Составить условия равновесия для системы сил, приложенных к рассматриваемому телу, и определить неизвестные. Эта система сил состоит из всех активных сил и всех реакций внешних связей.
Равновесие системы сходящихся сил
При решении некоторых задач оказывается целесообразным использование условий равновесия системы сходящихся сил в геометрической форме:
для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из сил системы, был замкнут.
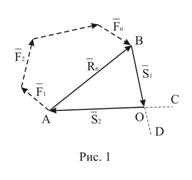 Геометрическую форму условий равновесия можно использовать в случае плоской системы сходящихся сил. Как правило, в ходе решения задачи требуется построить многоугольник, у которого все стороны известны по направлению и только две неизвестны по величине. В конечном счёте задача сводится к построению треугольника, поскольку всегда можно построить сумму
Геометрическую форму условий равновесия можно использовать в случае плоской системы сходящихся сил. Как правило, в ходе решения задачи требуется построить многоугольник, у которого все стороны известны по направлению и только две неизвестны по величине. В конечном счёте задача сводится к построению треугольника, поскольку всегда можно построить сумму ![]() заданных сил (рис.1). Построение треугольника начинается с заданной силы
заданных сил (рис.1). Построение треугольника начинается с заданной силы ![]() . Через начало и конец силы
. Через начало и конец силы ![]() проведём прямые (
проведём прямые (![]() и
и ![]() ), параллельные линиям действия неизвестных сил
), параллельные линиям действия неизвестных сил ![]() и
и ![]() . Таким образом определяется положение вершины
. Таким образом определяется положение вершины ![]() силового многоугольника и, следовательно, величины двух его сторон, длины которых равны модулям неизвестных сил
силового многоугольника и, следовательно, величины двух его сторон, длины которых равны модулям неизвестных сил ![]() и
и ![]() .
.
Можно проводить построение в определённом масштабе. Тогда величины неизвестных сил определяются измерением по чертежу длин соответствующих сторон. Однако, во многих случаях имеет смысл рассчитать силовой треугольник. При таком расчёте используют известные геометрические и тригонометрические положения: теорему Пифагора, теорему синусов, теорему косинусов, подобие и т. д. В некоторых случаях не очевидно, что действующая на тело система сил является сходящейся. Установить этот факт и определить линию действия реакции шарнира помогает теорема о трёх силах.
Условия равновесия системы сил, линии действия которых
расположены в одной плоскости
В условиях равновесия произвольной системы сил в рассматриваемом случае остаётся только три значащих уравнения:
![]()
![]()
![]()
 где
где ![]() – произвольно выбранная точка плоскости
– произвольно выбранная точка плоскости ![]() .
.
Моменты различных сил такой системы относительно любой точки плоскости отличаются друг от друга только величиной и знаком проекции на координатную ось ![]() . Поэтому при изучении плоской системы сил во многих учебниках вводят обозначение
. Поэтому при изучении плоской системы сил во многих учебниках вводят обозначение ![]() , понимая под ним проекцию на ось
, понимая под ним проекцию на ось ![]() момента силы относительно точки
момента силы относительно точки ![]() . В настоящей работе такое обозначение не используется. При этом для вычисления
. В настоящей работе такое обозначение не используется. При этом для вычисления 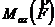 применимо простое правило:
применимо простое правило:
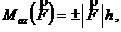
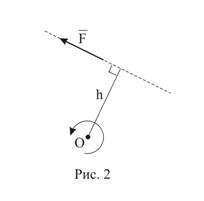
где ![]() – плечо силы, равное кратчайшему расстоянию от точки
– плечо силы, равное кратчайшему расстоянию от точки ![]() до линии действия силы; знак « + » соответствует повороту вокруг точки
до линии действия силы; знак « + » соответствует повороту вокруг точки ![]() против хода часовой стрелки (рис.2).
против хода часовой стрелки (рис.2).
Учёт пары сил при составлении уравнений равновесия
Рассмотрим особенности решения задач, в которых наряду с силами на тело действует пара сил ![]() с моментом
с моментом ![]() , расположенная в координатной плоскости
, расположенная в координатной плоскости ![]() .
.
При составлении уравнений равновесия следует учитывать, что в условия равенства нулю суммы проекций всех сил на любую координатную ось входящие в пару силы ![]() и
и ![]() никакого вклада не внесут, так как сумма проекций этих сил на любую координатную ось равна нулю (
никакого вклада не внесут, так как сумма проекций этих сил на любую координатную ось равна нулю (![]() ).
).
Вычислим сумму моментов сил, образующих пару, относительно оси ![]() (рис. 3).
(рис. 3).
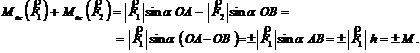
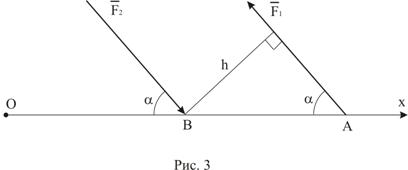
Таким образом, в уравнении моментов к моментам прочих сил алгебраически прибавляется момент пары, точнее проекция на ось ![]() вектора момента пары, взятая с соответствующим знаком. Проекция момента пары положительна, если с положительного конца оси
вектора момента пары, взятая с соответствующим знаком. Проекция момента пары положительна, если с положительного конца оси ![]() поворот пары виден против хода часовой стрелки.
поворот пары виден против хода часовой стрелки.
Общие замечания
Для получения наиболее простых уравнений равновесия имеет смысл одну из координатных осей проводить перпендикулярно возможно большему числу неизвестных сил, а за моментную принимать точку, через которую проходят линии действия возможно большего числа неизвестных сил.
Имеет смысл получать решение в общем виде (в буквенных обозначениях). Численные значения следует подставлять только на последнем этапе решения задачи.
Равновесие составных тел
При решении задач об определении опорных реакций может оказаться, что из составленных условий равновесия невозможно определить все неизвестные величины, так как их число больше числа уравнений, в которые эти неизвестные входят. Подобное может произойти по двум основным причинам.
Во-первых, на рассматриваемое тело могут быть наложены лишние связи, ненужные для обеспечения равновесия абсолютно твёрдого тела, но необходимые для предотвращения недопустимо больших деформаций. В этом случае задача определения реакций опор является статически неопределимой в том смысле, что невозможно определить реакции связей без учёта деформаций тела, т. е. оставаясь в рамках модели абсолютно твёрдого тела. Такие задачи в теоретической механике не рассматриваются.
Во-вторых, в качестве тела, равновесие которого рассматривается, может быть выбрана конструкция, состоящая из двух или более тел, соединённых между собой внутренними связями. На такую конструкцию заведомо приходится накладывать дополнительные связи, обеспечивающие равновесие конструкции. Основная особенность решения таких задач состоит в том, что необходимо рассматривать равновесие нескольких тел данной конструкции.
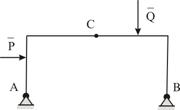
Рассмотрим, например, трёх шарнирную арку ![]() , нагруженную активными силами
, нагруженную активными силами ![]() и
и ![]() (рис. 4). Можно рассмотреть равновесие арки в целом. Тогда в систему внешних сил войдут заданные силы
(рис. 4). Можно рассмотреть равновесие арки в целом. Тогда в систему внешних сил войдут заданные силы ![]() и
и ![]() и силы реакций внешних опор – шарниров
и силы реакций внешних опор – шарниров ![]() и
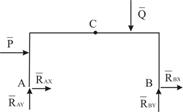
и ![]() . Соответствующая силовая схема представлена на рис. 5.
. Соответствующая силовая схема представлена на рис. 5.
|
| |
Рис. 4 | Рис. 5 |
Хотя такая арка не является абсолютно твёрдым телом, заранее известно, что она покоится и, следовательно, приложенные к ней силы удовлетворяют условиям равновесия. Наличие шарнира ![]() позволяет двум частям арки поворачиваться друг относительно друга. Для предотвращения такого поворота приходится усиливать одну из опор, например, ставить в точке
позволяет двум частям арки поворачиваться друг относительно друга. Для предотвращения такого поворота приходится усиливать одну из опор, например, ставить в точке ![]() шарнирно неподвижную опору вместо шарнирно подвижной. При этом число неизвестных составляющих сил реакций увеличивается – появляется
шарнирно неподвижную опору вместо шарнирно подвижной. При этом число неизвестных составляющих сил реакций увеличивается – появляется ![]() . Трёх уравнений равновесия недостаточно для определения четырёх неизвестных. Поэтому приходится рассматривать равновесие ещё какой-либо части конструкции, например, стержня
. Трёх уравнений равновесия недостаточно для определения четырёх неизвестных. Поэтому приходится рассматривать равновесие ещё какой-либо части конструкции, например, стержня ![]() .
.
|
| |
Рис. 6 | Рис. 7 |
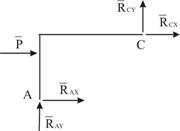
Для стержня ![]() шарнир
шарнир ![]() является внешней опорой, поэтому его реакция входит в систему внешних сил, действующих на
является внешней опорой, поэтому его реакция входит в систему внешних сил, действующих на ![]() (рис. 6). Для стержня
(рис. 6). Для стержня ![]() можно составить ещё три уравнения равновесия, которые вместе с уравнениями равновесия, составленными для арки
можно составить ещё три уравнения равновесия, которые вместе с уравнениями равновесия, составленными для арки ![]() , образуют систему шести уравнений, содержащих шесть неизвестных.
, образуют систему шести уравнений, содержащих шесть неизвестных.
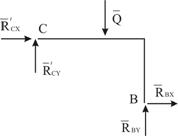
Можно рассмотреть равновесие правого стержня ![]() (рис. 7). При этом следует учитывать, что силы взаимодействия в шарнире
(рис. 7). При этом следует учитывать, что силы взаимодействия в шарнире ![]() подчиняются третьему закону Ньютона:
подчиняются третьему закону Ньютона: ![]() ;
; ![]() . Для решения поставленной задачи достаточно рассмотреть равновесие только двух из трёх тел в любой комбинации. Условия равновесия третьего тела могут быть использованы для проверки полученных результатов.
. Для решения поставленной задачи достаточно рассмотреть равновесие только двух из трёх тел в любой комбинации. Условия равновесия третьего тела могут быть использованы для проверки полученных результатов.
Универсальный метод решения подобных задач состоит в том, что конструкция разбивается на отдельные абсолютно твёрдые тела и рассматривается равновесие каждого из этих тел. Однако, во многих случаях такой подход оказывается нерациональным, поскольку приводит к необходимости решения системы уравнений, каждое из которых может содержать несколько неизвестных. Причём в уравнения может входить значительное число лишних неизвестных, которые не требуется определять по условиям решаемой задачи. Приобретя определённые навыки, можно поставить целью поиск наиболее рационального способа решения задачи, в основе которого лежит идея использования минимального числа уравнений, каждое из которых, по возможности, содержит только одну неизвестную.
В заключение подчеркнём ещё раз – необходимо рисовать отдельную силовую схему для каждого тела, равновесие которого рассматривается.
Приведение системы сил к простейшему виду
В основе решения первой основной задачи статики (приведение системы сил к простейшему виду) лежит теорема о приведении системы сил к одному центру. При решении задач о приведении системы сил к простейшему виду имеет смысл придерживаться определённой последовательности действий.
1. Вычислить главный вектор и главный момент заданной системы сил относительно выбранного (или заданного) центра приведения. Центр приведения, если возможно, следует принять за начало координат.
2. Вычислить второй статический инвариант и определить, к какому простейшему виду приводится заданная система сил.
3. Определить параметры простейшей силовой системы, эквивалентной заданной системе сил.
Приведение плоской системы сил к простейшему виду
 Приведённую здесь информацию можно рассматривать как методические указания к выполнению расчётно-графической работы.
Приведённую здесь информацию можно рассматривать как методические указания к выполнению расчётно-графической работы.
Если заданная система сил расположена в одной плоскости и число сил невелико, можно использовать чисто графический метод, основанный на использовании аксиомы о равнодействующей двух сил, приложенных в одной точке (аксиома 1).
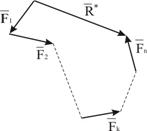
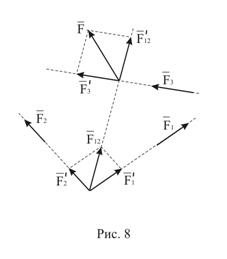
Рассмотрим систему трёх сил 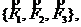 расположенных в одной плоскости (рис.8). Определив точку пересечения каких-либо двух сил, например,
расположенных в одной плоскости (рис.8). Определив точку пересечения каких-либо двух сил, например, ![]() и
и ![]() , перенесём силы вдоль их линий действия в эту точку и заменим равнодействующей
, перенесём силы вдоль их линий действия в эту точку и заменим равнодействующей ![]() Затем ищем точку пересечения линий действия построенной силы
Затем ищем точку пересечения линий действия построенной силы ![]() и следующей силы
и следующей силы ![]() Переносим эти силы в точку пересечения линий действия и заменяем одной силой. В рассматриваемом случае задача решена:
Переносим эти силы в точку пересечения линий действия и заменяем одной силой. В рассматриваемом случае задача решена:
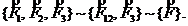
При большем количестве сил в системе аналогичные операции продолжаются до тех пор, пока в результате упрощений не останется только одна сила. Эта сила и будет равнодействующей.
Универсальный способ построения равнодействующей основан на использовании теоремы о приведении системы сил к одному центру. Центр приведения C(a, b,c) может быть выбран произвольно или задан по условию задачи. В том случае, когда заданная система сил расположена в одной плоскости, основные характеристики системы – главный вектор и главный момент можно вычислить различными способами, условно говоря, графически и аналитически. Наличие такой возможности может быть использовано для проверки полученных результатов.
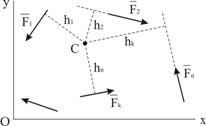
Рассмотрим систему сил 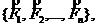 расположенную в координатной плоскости xy. Центр приведения C(a, b, О) также лежит в плоскости xy (рис.10). Остановимся сначала на графическом способе определения главного вектора и главного момента, практически применимом только для систем сил, расположенных в одной плоскости.
расположенную в координатной плоскости xy. Центр приведения C(a, b, О) также лежит в плоскости xy (рис.10). Остановимся сначала на графическом способе определения главного вектора и главного момента, практически применимом только для систем сил, расположенных в одной плоскости.
Главный вектор ![]() определяется как замыкающая сторона построенного в масштабе сил силового многоугольника (рис.9).
определяется как замыкающая сторона построенного в масштабе сил силового многоугольника (рис.9).
В случае плоской системы сил момент любой из сил относительно точки C перпендикулярен координатной плоскости xy, т. е. имеет ненулевую проекцию только на ось z. Проекция этого момента на ось z по модулю равна произведению модуля силы на кратчайшее расстояние от точки C до линии действия силы (плечо силы) и положительна, если с положительного конца оси z поворот тела вокруг точки C под действием силы виден против хода часовой стрелки (отрицателен в противоположном случае). Таким образом, проекцию на ось z главного момента относительно центра приведения C можно вычислить по формуле:
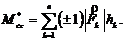
Плечи сил ![]() можно измерить с учётом выбранного масштаба расстояний по чертежу (рис.10). Таким образом,
можно измерить с учётом выбранного масштаба расстояний по чертежу (рис.10). Таким образом, ![]() где
где ![]() – единичный вектор координатной оси z.
– единичный вектор координатной оси z.
|
| |
Рис. 9 | Рис. 10 |
Вычислим главный вектор и главный момент плоской системы сил аналитически. Будем считать, что силы заданы своими проекциями на оси координат ![]() и приложены в точках
и приложены в точках ![]() Вычислим проекции главного вектора:
Вычислим проекции главного вектора: ![]() Тем самым мы определяем и проекции равнодействующей
Тем самым мы определяем и проекции равнодействующей ![]() на координатные оси, так как
на координатные оси, так как ![]() Модуль равнодействующей определяется по формуле:
Модуль равнодействующей определяется по формуле:
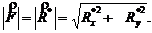
Вычислим главный момент системы сил относительно центра C. По определению главного момента
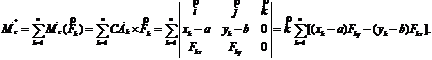 Отсюда:
Отсюда: ![]()
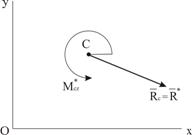
Остаётся упростить систему сил, состоящую из силы 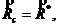 приложенной в точке C и пары сил с моментом
приложенной в точке C и пары сил с моментом ![]() (рис.11). Из всех пар, момент которых равен
(рис.11). Из всех пар, момент которых равен ![]() , построим одну
, построим одну ![]() таким образом, чтобы одна из сил этой пары
таким образом, чтобы одна из сил этой пары ![]() уравновешивала силу
уравновешивала силу ![]() . Для этого сила
. Для этого сила ![]() должна быть приложена в точке C и
должна быть приложена в точке C и 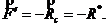 Вторая сила этой пары
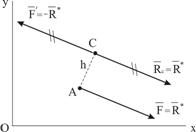
Вторая сила этой пары ![]() располагается в плоскости xy таким образом, чтобы с конца вектора
располагается в плоскости xy таким образом, чтобы с конца вектора ![]() поворот пары был виден против хода часовой стрелки (рис.12).
поворот пары был виден против хода часовой стрелки (рис.12).
|
| |
Рис. 11 | Рис. 12 |
Заметим, что при работе с плоской системой сил вектор главного момента обычно не изображают на чертеже. Указывают только направление вращения, создаваемого парой сил с моментом ![]()
Расстояние CA (плечо пары) определяется по формуле:
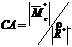
Уравновешенную систему сил 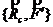 можно отбросить. Таким образом, заданная система сил заменена одной силой
можно отбросить. Таким образом, заданная система сил заменена одной силой ![]() , которая и будет равнодействующей.
, которая и будет равнодействующей.
При аналитическом способе решения задачи необходимо получить уравнение линии действия равнодействующей. В рассматриваемом случае плоской системы
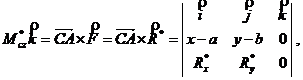
где x и y – координаты точки A, лежащей на линии действия равнодействующей. Отсюда получаем:
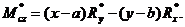
В общем случае, когда заданная система сил произвольным образом расположена в пространстве, возможен только аналитический способ решения задачи. Особенности решения такой задачи рассмотрим на примере.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО РАЗДЕЛУ
«КИНЕМАТИКА»
Кинематика точки
Успех решения задачи во многом зависит от правильного выбора системы координат. В частности, если траектория точки окружность, необходимо использовать естественные оси, поскольку в этом случае получаем простые формулы для вычисления ускорения точки.
Плоскопараллельное движение твёрдого тела
При вычислении скоростей точек плоской фигуры имеет смысл принимать за полюс мгновенный центр скоростей. При вычислении ускорений точек плоской фигуры имеет смысл за полюс принимать мгновенный центр ускорений, если его положение очевидно. Однако при вычислении ускорений определение положения мгновенного центра ускорений иногда бывает неоправданным и за полюс принимается точка, ускорение которой в данный момент времени известно.
Сложное движение точки
Чтобы увидеть относительную траекторию, относительную скорость и относительное ускорение точки, необходимо мысленно остановить переносное движение. Наоборот, чтобы увидеть переносную скорость и переносное ускорение точки, необходимо мысленно остановить точку в её относительном движении.
При определении направления ускорения Кориолиса (особенно в том случае, когда ось переносного вращения перпендикулярна плоскости относительного движения точки) удобно использовать правило Жуковского: чтобы получить направление ускорения Кориолиса, необходимо повернуть проекцию вектора относительной скорости на плоскость, перпендикулярную оси переносного вращения, в сторону переносного вращения на угол 900.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО РАЗДЕЛУ «ДИНАМИКА»
Выбор осей координат
Если траектория материальной точки окружность, необходимо использовать естественные оси, поскольку в этом случае получаем простые формулы для вычисления ускорения точки.
При исследовании колебаний материальной точки или механической системы начало отсчёта необходимо совмещать с положением статического равновесия, поскольку в этом случае постоянные силы не войдут в уравнения движения, но будут связаны отдельным уравнением – условием статического равновесия.
При качении колеса или скольжении тела по наклонной плоскости целесообразно одну из координатных осей направить вдоль наклонной плоскости, а вторую – по нормали к ней.
Решение задач при помощи общих теорем динамики
Если механическая система состоит из нескольких тел, связанных между собой, приходится, как правило, рассматривать движение каждого тела по отдельности. При этом необходимо для каждого тела изображать силовую и кинематическую схемы.
Применять теорему об изменении количества движения и теорему об изменении кинетического момента к системе в целом имеет смысл в тех случаях, когда система внешних сил обладает какой-либо особенностью. Например, если сумма проекций всех внешних сил на какую-либо ось равна нулю, то проекция количества движения на эту ось постоянная, что даёт возможность получить достаточно простые уравнения, связывающие кинематические характеристики системы.
Если в задаче требуется определить какую-либо кинематическую характеристику в зависимости от той или иной координаты системы, целесообразно использовать теорему об изменении кинетической энергии механической системы.
Элементы аналитической механики
Один из важных вопросов, возникающих при анализе движения механической системы – определение числа степеней свободы системы. Один из способов решения такой задачи состоит в следующем. Находим одно из возможных перемещений системы, которое можно задать одним параметром. Мысленно ликвидируем это возможное перемещение – задерживаем тело (или точку). Находим очередное возможное перемещение. Ограничиваем и его. Количество таких ограничений совпадает с числом степеней свободы системы.
При выборе обобщённых координат предлагается следующее. Если движение какого-либо тела определяется одной координатой (декартовой при поступательном движении или углом поворота при вращательном движении), то эту координату следует считать одной из обобщённых координат. Если другое тело может двигаться относительно первого (например, соединяется с ним при помощи пружины), то в качестве второй обобщённой координаты следует принять координату относительную (например, удлинение пружины) и т. д., идя от тела, совершающего простое движение.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. , , Курс теоретической механики. Лань. 2000 и последующие издания.
2. Сборник задач по теоретической механике. 2001 и последующие издания.
3. Краткий курс теоретической механики, 2000 и последующие издания.
4. , , С. Теоретическая механика в примерах и задачах.
5. Основные вопросы статики /, , М.: МГСУ, 2008.
6. Основные вопросы кинематики /, , . М.: МГСУ, 2008.
7. Основные вопросы динамики /, , . М.: МГСУ, 2009.
8. Статика. Сборник расчётно-графических заданий и контрольных работ / , . М.: МГСУ, 2009.
9. Кинематика. Сборник расчётно-графических заданий и контрольных работ /, , . М.: МГСУ, 2009.
О Г Л А В Л Е Н И Е
Кафедра теоретической механики ………………………... | 1 |
Методические рекомендации по организации изучения дисциплины ………………………………………………… | 5 |
План учебных занятий …………………………….............. | 7 |
Расчётно-графические работы и контрольные задания …. | 13 |
Методические указания по выполнению самостоятельной работы ……………………………………………………….. | 15 |
Библиографический список ……………………………….. | 29 |