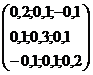Доходность и риск инвестиционного портфеля

Тема 1: Доходность и риск инвестиционного портфеля.

Формируя инвестиционный портфель, необходимо оценить его риск и доходность.

Для определения доходности портфеля, состоящего из N количества ценных бумаг в конце периода n, можно использовать следующую формулу:

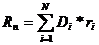, (1)

где Di –доля конкретного вида ценных бумаг в портфеле в момент его формирования;

ri –ожидаемая (или фактическая) доходность i-той ценной бумаги;

N - количество ценных бумаг в портфеле.

Риск портфеля измеряется среднеквадратическим отклонением фактической доходности портфеля от ожидаемой и определяется по формуле:

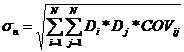, (2)

где - среднеквадратическое отклонение портфеля;

, - доля активов i и j в начальной стоимости портфеля;

- ковариация (взаимодействие или взаимозависимость) ожидаемых доходностей i-го и j-го активов.

Ковариация ожидаемых доходностей рассчитывается по формуле:

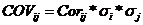, (3)

где Corij – коэффициент корреляции между ожидаемыми доходностями активов;

,- среднеквадратическое отклонение доходности i-го и j-го активов соответственно.

Оценить риск инвестиционного портфеля при вводе в его состав безрискового актива (как правило, безрисковыми активами являются ценные бумаги, эмитируемые государством)можно посредством следующей формулы:

, (4)

где - риск портфеля вследствие включения в его состав безрискового актива;

Dn – доля, занимаемая прежним портфелем в формируемом;

- риск прежнего портфеля.

Приведенная формула свидетельствует о том, что введение в портфель безрискового актива снижает совокупный риск портфеля (однако при этом будет снижаться и доходность). Поэтому инвестор, негативно относящийся к риску, выбирает большую долю безрисковых активов в инвестиционном портфеле, платой за это является некоторая потеря в доходности.

Чем выше инвестор оценивает риск проекта, тем более высокие требования он обычно предъявляет к его доходности. Это может быть отражено в расчетах путем соответствующего увеличения нормы дисконта – включения в нее премии за риск.

Существует две группы методов – агрегированные и пофакторные (кумулятивные), учитывающие риск сразу целиком и каждый вид риска в отдельности соответственно.

Метод бета-коэффициента для расчета нормы дисконта использует модель оценки оценки капитальных активов (САРМ):

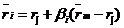, i = 1,2,…,n, (5)

где - ожидаемая (требуемая) доходность i- го рискованного актива;

- безрисковая ставка дохода;

-общая доходность рынка в целом (среднерыночного портфеля ценных бумаг).

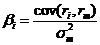- бета коэффициент рискованных активов i-го вида, i=1,2,…,n (6).

Равновесный рынок рискованных активов удовлетворяет модели оценки финансовых активов в одном из следующих случаев:

1)  рынок является совершенным;

2)  рынок является почти совершенным, а инвесторы не склонны к риску.

Прямая, заданная уравнением

, (7), где r- требуемая инвестором ставка дохода (на собственный капитал) - называется линией рынка рискованных активов.

Среднерыночная доходность должна рассматриваться как известная абстракция, поскольку полная информация о доходности всех обращающихся на рынке акций обычно отсутствует. На практике этот показатель рассчитывают по ограниченному числу представительных ценных бумаг, например, по акциям «голубых фишек». Обычно коэффициент лежит в пределах от 0 до 2. Для рынка в целом коэффициент равен 1.

Интерпретация бета-коэффициента для акций конкретной компании заключается в следующем:

=1, означает, что акции данной компании имеют среднерыночную степень риска;

<1, означает, что ценные бумаги данной компании менее рискованны, чем в среднем на рынке;

>1, означает, что ценные бумаги данной компании более рискованны, чем в среднем на рынке. [1]

Пример: Рассматривается целесообразность инвестирования в акции компании А, имеющей β=1,6, или компании Б, имеющей β=0,9, если rf=6%; rm= 12%. Инвестиция делается в том случае, если доходность составляет не менее 15%.

Необходимые для принятия решения оценки можно рассчитать с помощью модели САРМ. По формуле (5) находим:

для компании А: ,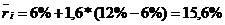

для компании В: .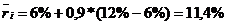

Таким образом, инвестиции в акции компании А более целесообразны.

Важным свойством модели САРМ является ее линейность относительно степени риска. Это дает возможность определить -коэффициент портфеля, как средневзвешенную -коэффициентов входящих в портфель финансовых активов.

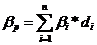, (8) где

- значение бета-коэффициента i-го актива в портфеле;

- значение бета-коэффициента портфеля;

- доля i-го актива в портфеле;

n – число различных финансовых активов в портфеле.

Пример: Портфель включает следующие активы:

12% акции компании А, имеющие β =1;

18% акции компании В, имеющие β =1,2;

25% акции компании С, имеющие β =1,8;

45% акции компании D, имеющие β =0,7.

Тогда β-коэффициент инвестиционного портфеля будет равен:

βр=0,12*1+0,18*1,2+0,25*1,8+0,45*0,7=1,10

Метод бета-коэффициента используется при установлении нормы дисконта для денежного потока только собственного капитала. Если необходимо установить норму дисконта для денежного потока всего инвестированного капитала, используют метод средневзвешенной стоимости капитала(WACC). В наиболее простом случае, когда в структуре инвестированного капитала вычленяются только собственные и заемные средства (без их дальнейшего подразделения), расчетная формула нормы дисконта имеет следующий вид:

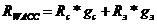, (9)

где - стоимость собственного капитала (требуемая отдача на акции);

- стоимость заемного капитала (ставка процента по займу);

,- доли собственного и заемного капитала в общем капитале проекта.

Задача №1.

Ожидаемая доходность рыночного портфеля =14%, а стандартное отклонение его доходности = 40%.

Определить бета-коэффициент рискованного актива, если ковариация между доходностью этого актива и доходностью рыночного портфеля равна:

а) 0,15;

б) 0,2;

в) -0,1.

Ответ: а)β=; r=13,56%; б) β=; r=15,75%; в)β=; r=2,63%.

Задача №2.

Ожидаемая доходность рыночного портфеля =12%, стандартное отклонение его доходности = 50%, безрисковая процентная ставка =6%. Определить ковариацию между доходностью рискованного актива и доходностью рыночного портфеля, если ожидаемая равновесная доходность этого актива равна:

а) 10%;

б) 20%;

в) 5%.

Ответ: а) cov (rm, r)= ; б) cov (rm, r)= ; в) cov (rm, r)= .

Задача №3.

Построить линию рынка рискованных активов, если =12% и rf = 8%. Определить равновесную ожидаемую доходность рискованного актива, если его бета-коэффициент равен

а) 1,5;

б) 0,8;

в) -1,2.

Ответ: r=0,08+0,04β; а) r=14%;б) r=11,2%; в) r=3,20% .

Задача №4.

Найти бета-коэффициент рискованного актива, если =16% и rf =7%, а равновесная ожидаемая доходность равна:

а) 20%;

б) 10%;

в) 5%.

Ответ: а)β=; б) β=; в)β=.

Задача №5.

На рынке имеются рискованные активы трех видов. Информация о рынке следующая (таблица 1):

Определить равновесные ожидаемые доходности рискованных активов, если ожидаемая доходность рыночного портфеля равна 12%, а безрисковая процентная ставка rf =7%.

Ответ: а) r=6,38%;б) r=12,95%; в) r=12,54% .

Вопросы:

О чем будет свидетельствовать увеличение бета-коэффициента в динамике для ценной бумаги конкретной компании? (о том, что вложения в ценные бумаги данной компании становятся более рискованными).

А о чем тогда будет свидетельствовать уменьшение бета-коэффициента в динамике для ценной бумаги конкретной компании? (о том, что вложения в ценные бумаги данной компании становятся менее рискованными).

[1] С 1995 года -коэффициенты публикуются в газете «Финансовые известия».