Теория и методика обучения и воспитания

На правах рукописи

ФЕДОТОВА Татьяна Ивановна

ПРОФЕССИОНАЛЬНО ОРИЕНТИРОВАННЫЕ ЗАДАЧИ

КАК СОДЕРЖАТЕЛЬНЫЙ КОМПОНЕНТ МАТЕМАТИЧЕСКОЙ ПОДГОТОВКИ СТУДЕНТОВ

ТЕХНИЧЕСКОГО ВУЗА В УСЛОВИЯХ УРОВНЕВОЙ

ДИФФЕРЕНЦИАЦИИ

13.00.02 – теория и методика обучения и воспитания

(математика, уровень профессионального образования)

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата педагогических наук

Красноярск 2009

Работа выполнена в ГОУ ВПО «Омский государственный педагогический университет»

Защита состоится «11» декабря 2009 г. в 12.00. часов на заседании диссертационного совета ДМ 212.099.16 при Сибирском федеральном университете г. Красноярск, , ауд. Ж 2-15.

С диссертацией можно ознакомиться в библиотеке Сибирского федерального университета г. Красноярск, ул. Академика Киренского, д. 26, ауд. Г 2-74.

Автореферат разослан «____» ноября 2009 г.

Ученый секретарь

диссертационного совета

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность исследования. Современный этап модернизации россий­ского образования выдвигает повышенные требования к качеству профессио­нальной подготовки инженера. Основная цель профессионального образования – подготовка высококвалифицированного специалиста соответствующего уровня и профиля, конкурентоспособного на рынке труда, компетентного, от­ветственного, свободно владеющего своей профессией. Это требует новых, бо­лее эффективных путей организации учебно-воспитательного процесса в тех­ническом вузе.

Сегодня актуальной категорией в теории высшего профессионального об­разования становится «профессиональная компетентность». Проблемы формирования профессиональной компетентности в различных сферах профес­сиональной деятельности в условиях прикладной направленности процесса обучения нашли отражение в работах , , , , и др.

Значительную роль в подготовке будущих инженеров играет мате­матическое образование. Обязательными требованиями математического образо­вания в техническом вузе являются следующие: непрерывность изучения и при­менения математики; фундаментальность математической подготовки; ориенти­рованность курса математики на практику; равноценность матема­тической подго­товки для всех форм обучения по одной и той же специальности; преемственность математической подготовки на всех ступенях образования. В техническом вузе математика выступает как особая образовательная дисциплина, так как знания, полученные по математике, являются фундаментом для изучения других общеоб­разовательных, общеинженерных и специальных дисциплин.

Анализ практики обучения математике студентов технических вузов пока­зывает, что качество математической подготовки не отвечает требованиям совре­менного производства. Результаты констатирующего эксперимента показывают, что более половины студентов технических вузов имеют удовлетворительные знания по математике.

Проблема математической подготовки будущих инженеров рассматрива­лась многими исследователями. Основными направлениями ее решения явля­ются: 1) совершенствование содержания курса высшей математики в техниче­ском вузе (, и др.); 2) повышение уровня подго­товки абитуриентов (, , и др.); 3) профессиональная направленность обучения математике че­рез содержательный компонент (прикладные задачи межпредметного харак­тера, профессионально ориентированные математические задачи, математиче­ское моделирование и др.), через методический компонент (проблемное, кон­текстное обучение, самостоятельная исследовательская деятельность, сочета­ние коллективных и индивидуальных форм обучения) и  мотивационно-психо­логический компонент (, , и др.); 4) компьютеризация обучения математике (, , и др.).

В то же время в этих исследованиях недостаточно изучена такая проблема совершенствования математической подготовки студентов транс­портных и нефтегазовых направлений технического вуза как выявление воз­можностей формирования мотивационного компонента, усиления прикладной направленности содержательного и процессуального компонентов методиче­ской системы обучения средствами профессионально ориентированных мате­матических задач в условиях уровневой дифференциации, что, в конечном счете, способствует формированию профессиональной компетентности. В ра­боте под дифференциацией обучения понимается разделение компонентов педа­гогической системы в зависимости от индивидуальных особенностей обучаю­щихся.

В нормативных документах, относящихся к организации, содержанию и технологии процесса обучения математике студентов технических вузов, обо­значена проблема реализации уровневой дифференциации, но не указаны кон­кретные пути и средства ее решения, в частности, остается малоизученным во­прос об организации индивидуальной траектории движения студента в учебном процессе в условиях различных форм организации учебно-познавательной дея­тельности, что в значительной степени отвечало бы его способностям, интере­сам и склонностям, его персонофицированности.

В настоящее время имеют место противоречия между:

-  потребностью общества в высококвалифицированном инженере, способ­ном решать современные математически ёмкие профессиональные за­дачи, и недостаточной подготовленностью будущих инженеров к этой деятель­ности;

-  необходимостью формирования профессиональной компетентности сту­дентов технического вуза и недостаточной разработанностью в педагогиче­ской теории основ формирования ее компонентов;

-  имеющимися потенциальными возможностями, способствующими фор­мированию профессиональной компетентности студентов технических ву­зов в процессе обучения математике, и недостаточной разработанностью мето­дики обучения, позволяющей реализовать этот потенциал;

-  разнообразием интересов, склонностей, способностей студентов, их пер­сонофицированностью и однообразием форм и методов, используемых в процессе обучения.

Выявленные противоречия позволили сформулировать проблему исследования – каковы должны быть содержательный и процессуальный компо­ненты методики обучения математике студентов транспортных и нефтегазовых направлений технического вуза, чтобы они обеспечивали качественную мате­матическую подготовку будущих инженеров в условиях уровневой дифферен­циации.

Цель исследования: теоретическое обоснование и разработка методики обучения математике на основе использования профессионально ориентиро­ванных математических задач в условиях уровневой дифференциации, способ­ствующая качественной математической подготовке студентов технического вуза, как важнейшей части его профессиональной готовности.

Объект исследования: процесс обучения студентов технических вузов математике.

Предмет исследования: методика обучения математике студентов транспортных и нефтегазовых направлений технического вуза с использова­нием профессионально ориентированных математических задач в условиях уровневой дифференциации.

Гипотеза исследования: если процесс обучения математике студентов технического вуза реализовать в рамках дифференцированного подхода, ис­пользуя средства профессионально ориентированных задач, то это позволит по­высить качество их математической подготовки и будет способствовать фор­мированию квалификационного, психологического и социального компонентов профессиональной компетентности.

Исходя из цели исследования и выдвинутой гипотезы, были поставлены следующие задачи исследования:

1.  Определить психолого-педагогические основы профессиональной подго­товки студентов технических вузов при обучении математике в условиях компетентностного подхода.

2.  Выявить роль и определить место профессионально ориентированных ма­тематических задач в профессиональной подготовке студентов технических вузов.

3.  Разработать структурно-функциональную модель процесса формирова­ния квалификационного, психологического и социального компонентов про­фессиональной компетентности студентов технических вузов в процессе обучения реше­нию профессионально ориентированных математических задач, определить на­правления ее реализации в условиях уровневой дифференциации.

4.  Разработать комплекс профессионально ориентированных математических задач, который строится на основе связи математики и спецдис­циплин на уровне знаний и видов деятельности и обеспечивающий сопровожде­ние процесса формирования профессиональной компетентности студентов технических вузов.

5.  Разработать методику обучения математике студентов транспортных и нефтегазовых направлений технических вузов на основе использования выделенного комплекса профессионально ориентированных математических задач и лабораторного практикума, способствующего формированию профес­сиональной компетентности студентов в условиях уровневой дифференциации, и экспериментально проверить ее эффективность.

Теоретико-методологической основой исследования являются: кон­цепция деятельностного подхода к обучению математике (, , и др.); концеп­ция профессиональной компетентности специалиста (, , и др.); положения теории индивидуализации и дифференциации обучения (, , и др.); теории организа­ции учебно-познавательной деятельности обучающихся (, , и др.); теории обучения решению задач, в частности профессионально ориентированных (, , и др.); теории моделирования педагогических процессов (, , и др.); исследования по проблемам профессионального образования (, и др.);

Для решения поставленных задач использовались следующие методы исследования: анализ философской, психолого-педагогической, математической, методической, учебной литературы, диссертационных работ по теме исследования, вузовских учебных планов, учебной документации, программ по математике и специальным дисциплинам для инженерных специальностей; анкетирование студентов и преподавателей и беседы с ними; наблюдение за ходом учебного процесса; педагогический эксперимент (конста­тирующий, поисковый и формирующий) и статистическая обработка его результатов.

Научная новизна проведенного исследования заключается в том, что:

1. Обоснована возможность и целесообразность формирования у студентов транспортных и нефтегазовых направлений в процессе обучения математике функциональных, мотивационно-волевых, рефлексивных, коммуникативных компетенций, соответствующих покомпонентному составу профессиональной компетентности.

2. В соответствии с выделенными компонентами профессиональной компетентности и уровнями сформированности проведена классификация профессионально ориентированных математических задач и определены соответствующие группы задач.

3. Разработана структурно-функциональная модель формирования профессиональной компетентности студентов транспортных и нефтегазовых направлений в процессе обучения решению профессионально ориентированных математических задач в условиях уровневой дифференциации.

4. Разработана методика обучения математике студентов транспортных и нефтегазовых направлений на основе использования выделенного комплекса профессионально ориентированных математических задач и лабораторного практикума, способствующего формированию профессиональной компетентности студентов в условиях уровневой дифференциации.

Теоретическая значимость исследования:

-  теория и методика обучения математике обогащена знаниями об особенностях формирования квалификационного, психологического, социального компонентов профессиональной компетентности студентов техни­ческого вуза в условиях уровневой дифференциации;

-  определены уровни сформированности квалификационного компонента профессиональной компетентности будущих инженеров, которые соотнесены с уровнями сложности профессионально ориентированных математических задач, обеспечивающих реализацию уровневой дифференциа­ции;

-  разработана структурно-функциональная модель формирования профессиональной компетентности будущих инженеров в процессе обучения решению профессионально ориентированных задач по математике в условиях уровневой дифференциации, трансформируемая и в другие частные методики.

Практическая значимость исследования:

-  составленный комплекс профессионально ориентированных задач по ма­тематике для студентов технических вузов и описанные формы обучения, используемые при их решении, обеспечили качественную математическую подготовку обучающихся;

-  основные положения разработанной и апробированной методики обуче­ния студентов технических вузов решению профессионально ориентированных математических задач могут быть использованы и в процессе обучения естественнонаучным дисциплинам;

-  разработан лабораторный практикум, обеспечивающий коллективную, групповую и индивидуальную формы взаимодействия студентов в учебном процессе, и направленный на обучение студентов математическому моделированию технических объектов, процессов и явлений с использованием компьютерных средств.

Результаты исследования могут быть использованы при подготовке лек­ционных и практических занятий, для разработки сборников задач, учебных и методических пособий для студентов технических вузов.

Достоверность и обоснованность результатов и выводов исследования обеспечены: методологией исследования; современными психолого-педагогическими теориями и концепциями; комплексом теоретических и эмпирических методов, адекватных объекту, предмету, цели и задачам исследования; педагогическим экспериментом и статистической обработкой его результатов.

Положения, выносимые на защиту:

1.  Уровневая дифференциация, реализуемая в обучении математике, позволяет организовать индивидуальные траектории движения студентов технических вузов в учебном процессе, что создает комфортные, благоприятные условия для успешного формирования психологического, квалификационного и социального компонентов профессиональной компетентности будущих инженеров.

2.  Специальный комплекс профессионально ориентированных математических задач, который строится на основе связи математики и спец­дисциплин на уровне знаний и видов деятельности, обеспечивает профес­сиональную подготовку студентов технических вузов в процессе обучения ма­тематике.

3.  Предложенная в диссертации методика математической подготовки студентов технических вузов, позволяет достичь планируемых результатов при такой организации учебно-познавательной деятельности, при которой обучающиеся выступают субъектами познания, чему способствует лаборатор­ный практикум, содержание которого строится с учетом требований уровневой дифференциации.

Апробация результатов исследования осуществлялась в форме выступ­лений с докладами на: Всероссийской конференции «Учитель в современных моделях обучения» (Томск, 2002), Всероссийской научной конференции «Со­временные проблемы математического и физического образования в школе и вузе» (Стерлитамак, 2006), V межвузовской научно-практической конференции студентов и аспирантов «Молодежь, наука, творчество» (Омск 2007), VIII Все­российской научно-практической конференции «Наука и молодежь» (Нижний Новгород, 2007), II Всероссийской научно-практической конференции «Акту­альные вопросы методики преподавания математики и информатики» (Биро­биджан, 2007), III международной научной конференции «Математика. Образо­вание. Культура» (Тольятти, 2007).

По теме исследования имеется 14 публикаций (статьи, тезисы, учебное пособие), среди них четыре в журналах, рекомендованных ВАК РФ.

Организация экспериментальной работы.

Экспериментальная база исследования: ГОУ ВПО «Омский государственный технический университет».

На первом этапе (2004–2005 гг.) проведен констатирующий эксперимент. Он характеризовался изучением и анализом теоретической и научно-методиче­ской литературы по теме исследования и вузовской практики обучения студен­тов. Разрабатывались учебно-методические материалы. На втором этапе (2005–2007 гг.) проведен поисковый эксперимент. Он характеризовался про­должением исследования особенностей и условий формирования профессио­нальной компетентности специалистов. Сформулирована рабочая гипотеза. Ве­лась разработка учебного пособия «Профессионально ориентированные задачи по математике для студентов инженерных специальностей». На третьем этапе (2007–2009 гг.) проведен формирующий эксперимент, обобщены результаты экспериментальной работы, оформлен текст диссертации.

Структура диссертационной работы определена логикой научного ис­следования. Диссертация состоит из введения, двух глав, заключения, библио­графического списка использованной литературы и приложения.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность темы исследования, поставлена проблема, определены объект, предмет, цель, сформулированы гипотеза, задачи исследования, его методологические и теоретические основы, охарактеризо­ваны научная новизна, теоретическая и практическая значимость работы, сформулированы основные положения, выносимые на защиту.

В первой главе «Теоретические основы математической подготовки студентов технического вуза в условиях уровневой дифференциации, содержательным компонентом которой являются профессионально ориентированные задачи» раскрыта сущность и определены компоненты профессиональной подготовки студентов технического вуза, показаны роль и место профессионально ориентированных математических задач в формировании профессиональной компетентности будущих инженеров, обоснована целесообразность реализации дифференцированного подхода в процессе обучения решению профессионально ориентированных математических задач с целью профессиональной подготовки студентов технического вуза.

В первом параграфе выявлены и охарактеризованы проблемы профессиональной подготовки студентов технических вузов в процессе обучения математике; через анализ ближайших родовидовых понятий (компетентность, компетенция) раскрыта сущность понятия «профессиональная компетентность». В работе под компетенциями понимается комплекс взаимосвязанных качеств личности, выражающихся в мобилизации знаний, умений, опыта, поведения и готовности личности к эффективному решению задач и проблем, касающихся определенного круга вопросов в какой-либо сфере деятельности; профессиональная компетентность определена как интегральная характеристика личности, представляемая комплексом компетенций в профессиональной сфере деятельности, включающая его личностное отношение к ней и ее предмету.

На основании проведенного исследования выделены компоненты профессиональной компетентности: психологический, квалификационный, социальный. Указанные компоненты проявляются в следующих компетенциях: психологический – в мотивационно-волевых и рефлексивных компетенциях; квалификационный – в функциональных компетенциях; социальный – в коммуникативных компетенциях. В работе проведена конкретизация компонентов профессиональной подготовки (табл. 1).

Таблица 1

Конкретизация компонентов профессиональной подготовки студентов технического вуза в процессе обучения математике профессиональными компетенциями (фрагмент)

Во втором параграфе рассмотрены различные подходы к определению понятия «задача», на основе чего определена сущность профессионально ориентированной математической задачи, трактуемой как задачи, условие и требование которой определяют собой модель некоторой ситуации, возникающей в профессиональной деятельности инженера, а исследование этой ситуации осуществляется средствами математики и способствует профессиональному развитию личности специалиста. Определены их роль и место в формировании профессиональной компетентности будущих инженеров. В работе рассмотрены критерии отбора и конструирования профессионально ориентированных математических задач, описаны их виды: проектно-конструкторские, организационно-управленческие, производственно-технологические, исследовательские.

Решая профессионально ориентированные математические задачи, студенты, как правило, строят и исследуют математические модели изучаемых явлений, что формирует и развивает навыки математического моделирования объекта к познанию другого или других объектов. Модель – некоторая реально существующая или мысленно представляемая система, которая, замещая и отображая в познавательных процессах другую систему – оригинал, находится с ней в отношении сходства (подобия), благодаря чему изучение модели позволяет получить информацию об оригинале. В работе описаны три этапа математического моделирования.

1.Формализация – переход от ситуации, которую необходимо разрешить, к ее формальной математической модели, к четко поставленной математической задаче.

На этом этапе студенты должны научиться выделять основные взаимосвязи между компонентами условия задачи, анализировать полноту имеющихся данных, выражать математическими символами те положения и их взаимосвязи, которые даны в условии задачи. Как правило, именно формализация профессиональной задачи, «перевод» ее на математический язык вызывает наибольшие затруднения.

2.Внутримодельное решение – решение поставленной математической задачи методами, развитыми в самой математике для задач данного типа.

На этом этапе студенты учатся выбирать наиболее адекватный метод для исследования поставленной математической задачи, разбивать сложные задачи на подзадачи, пользоваться вспомогательным математическим аппаратом, выбирать приемы решения и определять наиболее эффективные программные средства для исследования модели.

3.Интерпретация – сопоставление полученного математического ответа с исходной ситуацией и перевод его на язык исходной ситуации.

На этом этапе студенты должны научиться делать качественные выводы на основании математического решения и компьютерного анализа модели, выявлять соответствие полученных результатов рассматриваемой ситуации, оценивать значение определенных факторов для практической деятельности.

В третьем параграфе проанализированы различные аспекты концепции дифференцированного подхода к обучению, определены условия, обеспечивающие эффективность реализации уровневой дифференциации.

В работе приведены уровневые характеристики компонентов профессио­нальной компетентности будущего инженера (интуитивный, нормативный, креативный) (табл. 2).

Таблица 2

Уровневые характеристики компонентов профессиональной компетентности будущих инженеров (фрагмент)

Профессионально ориентированные математические задачи представлены тремя уровнями сложности и соотнесены с уровнями сформированности квалификационного компонента профессиональной компетентности будущих инженеров (табл. 3). Анализ содержания таблицы дает возможность выделить задачи, связанные с решением профессионально ориентированных математических задач (в таблице эти задачи выделены курсивом).

Разработана структурно-функциональная модель процесса формирова­ния профессиональной компетентности будущих инженеров в процессе обуче­ния решению профессионально ориентированных задач по математике в усло­виях уровневой дифференциации (рис. 1). В модели отражено поэтапное формирование профессиональной компетентности студентов технических вузов.

На первом этапе, мотивационно-ориентировочном, происходит обосно­вание целей формирования профессиональной компетентности студентов технических вузов. Действия преподавателя на данном этапе должны быть направлены на формирование положительного отношения студентов к овладению профессиональными компетенциями и развитие познавательного интереса.

Таблица 3

Задачи различных уровней сложности, способствующие формированию квалификационного компонента профессиональной компетентности студентов технического вуза при обучении математике

Уровни сформиро­ванности	Уровень усвоения знаний, формирования умений и навыков	Уровень сложности задачи	Задачи
		ИН­ТУИ­ТИВ­НЫЙ	I уровень – формирование умений и навыков в процессе решения задач, алгоритм решения которых известен (алгоритмические, тренировочные задачи являются преобладающими).	Распознавание объектов.	§Распознавание понятий, правил, формул, геометрических объектов.
Воспроизведение (формули­ровка).	§ Воспроизведение отдельных фактов, правил. § Перечисление и описание отдельных свойств, признаков основных понятий. § Формулировка основных аксиом, определений, теорем. § Графическая иллюстрация некоторых определений, понятий, свойств, теорем.
Простые задачи на операции с данными.	§Простые вычислительные задачи с применением основных формул, схем. §Задачи, направленные на формирование и усвоение основных понятий, формул, теорем. §Задачи на применение основных понятий, формул, теорем. §Задачи на построение по заданным формулам (графики, функции, геометрические интерпретации).
НОРМА­ТИВ­НЫЙ		II уровень – формирование умений и навыков в процессе решения задач, когда алгоритм известен не полно­стью (сведение к известным алго­ритмам или суперпозиция ряда из­вестных алгоритмов).	Распознавание объектов.	§На составление и различие основных понятий, формул, свойств, графиков, геометрических объектов.
Воспроизведение (формули­ровка).	§Перечисление и описание системы фактов, понятий, свойств, признаков с сопоставлением и различием. §Умение распределять и классифицировать (свойства, понятия, признаки). §Воспроизведение теоретических положений (без доказательства), определенных алгоритмов. §Доказательство основных свойств, теорем по известному алгоритму.
Задачи на формирование основных структурных элементов зна­ний.	§Задачи с анализом и выявлением взаимоотношений между отдельными фактами и доказательст­вом основных свойств, формул, теорем (систематизация).
Задачи на сложные операции с дан­ными.	§Задачи на применение основных формул, схем: а) трудоемкие вычислительные операции; б) задачи с геометрическими иллюстрациями в процессе их решения. §Задачи на комбинацию известных алгоритмов. §Задачи, когда алгоритм их решения студентам известен не полностью.
КРЕАТИВ­НЫЙ		III уровень – формирование умений и навыков решения задач, когда алгоритм не известен (исследова­тельские или эвристические).	Сложные задачи на операции с данными.	§  Комбинированные задачи, решение которых предполагает использование нескольких известных алгоритмов, интеграцию математических методов. §  Задачи с поиском оптимального решения в известной ситуации.
Задачи творческого характера.	§  Задачи, связанные с углублением и развитием знаний по теории. §  Составление задач, анализ задач с недостающими или избыточными исходными данными, анализ и по­иск ошибок в решении задач. §  Профессионально ориентированные задачи исследовательского характера.

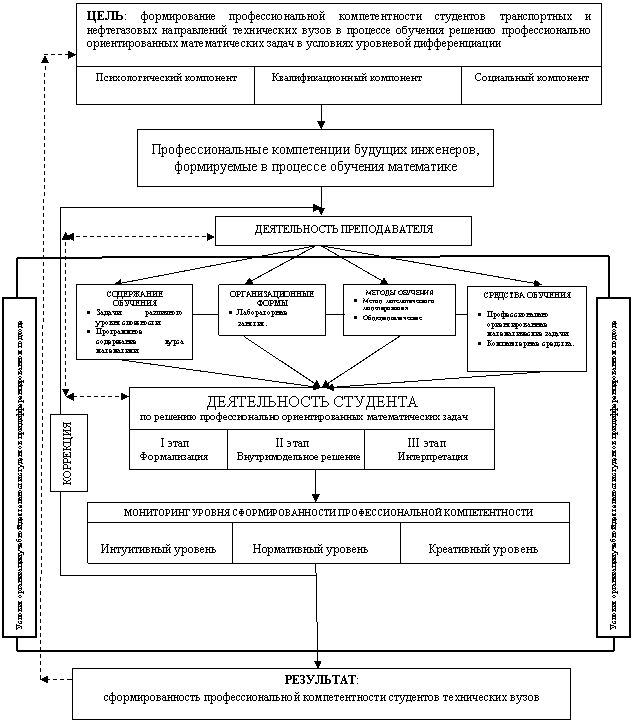Рис. 1. Структурно-функциональная модель формирования профессиональной компетентности студентов транспортных и нефтегазовых направлений в процессе обучения решению профессионально ориентированных математических задач в условиях уровневой дифференциации

На втором этапе, деятельностно-операционном, формирование профес­сиональной компетентности начинается с решения студентами профессио­нально ориентированных математических задач, направленных на овладение функциональными компетенциями, в условиях фронтальной, парной, группо­вой и индивидуальной работы. Затем организуется работа по решению студен­тами профессионально ориентированных математических задач на лаборатор­ных занятиях.

На третьем этапе, контрольно-оценочном, осуществляется контроль сформированности уровня овладения студентами профессиональными компе­тенциями и проводится работа, обеспечивающая переход обучающихся на бо­лее высокие уровни.

Вторая глава «Содержание и особенности методики обучения математике студентов технического вуза на основе использования профессионально ориентированных математических задач в условиях уровневой дифференциации» состоит из трех параграфов.

В первом параграфе приведена характеристика комплекса профессио­нально ориентированных математических задач различных уровней сложности, составленного в соответствии с выделенными в первой главе компонентами профессиональной компетентности и отвечающего следующим требованиям:

1.Профессионально ориентированные задачи комплекса должны:

а)  описывать ситуацию, возникающую в профессиональной деятельности инженера;

б)  содержать неизвестные характеристики некоторого профессионального объекта или явления, которые надо исследовать по имеющимся известным ха­рактеристикам с помощью средств математики;

в)  способствовать прочному усвоению математических знаний, приемов и методов, являющихся основой профессиональной деятельности инженера;

г)  обеспечивать установление взаимосвязей математики со специальными дисциплинами;

д)  анализ содержания задачи и ее решение должны требовать знаний по специальным предметам;

е)  определять пропедевтический этап изучения понятий специальных дис­циплин.

2.  Задачи комплекса должны быть направлены на формирование квалификационного компонента профессиональной компетентности будущих инженеров.

3.  Профессионально ориентированные задачи должны быть направлены на достижение более высокого уровня сформированности профессиональной компетентности будущих инженеров.

В работе приводятся примеры заданий из разных разделов курса матема­тики в соответствии с классификацией задач (табл. 3) в контексте требований уровневой дифференциации.

При решении профессионально ориентированных математических задач, направленных на формирование интуитивного уровня квалификационного

Приведем пример такой профессионально ориентированной задачи на тему «Матрицы и действия над ними»:

Задача 1. Омский агрегатный завод и Омский приборостроительный завод им.  поставляют на предприятия генераторы электрической энергии: синхронные М, асинхронные N и постоянного тока P большой, средней и низкой мощности. Количество поставленных каждым заводом генераторов по каждой категории мощности характеризуется следующей таблицей (табл. 4):

Таблица 4

Каков общий выпуск изделий по указанным уровням производительно­сти?

При изучении различных учебных тем по математике профессионально ориентированные задачи подобного типа применяются для более глубокого ус­воения соответствующих математических понятий, приобретения и закрепле­ния навыков решения задач инженерно-практического содержания.

Профессионально ориентированные задачи, направленные на формирование интуитивного уровня квалификационного компонента профессиональной компетентности будущих инженеров, – это задачи на прямое применение в знакомой ситуации известных фактов, стандартных приемов, распознавание математических объектов и свойств, выполнение стандартных процедур, применение известных алгоритмов и технических навыков, работа со стандартными, знакомыми выражениями и формулами, непосредственное выполнение вычислений.

Алгоритм решения профессионально ориентированных математических задач, направленных на формирование нормативного уровня квалификацион­ного компонента профессиональной компетентности будущих инженеров, из­вестен не полностью. Приведем пример такой задачи.

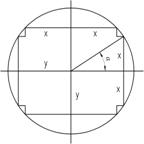
Задача 2. Форма поперечного сечения магнитопровода силового трансформатора по условиям технологичности изготовления должна иметь вид, показанный на рисунке 2. С целью уменьшения общих размеров трансформатора нужно как можно больше заполнить середину железным сердечником. Вычислить и , если радиус поперечного сечения магнитопровода равен . Рис. 2

Профессионально ориентированные задачи, направленные на формиро­вание нормативного уровня квалификационного компонента профессиональной компетентности будущих инженеров, не являются типичными, но все же зна­комы студентам или выходят за рамки известного лишь в очень незначительной степени. Содержание задачи подсказывает, какой раздел математики надо использовать и какие известные методы применить. Обычно в этих задачах присутствует больше требований к интерпретации решения, они предполагают установление связей между разными представлениями ситуации, описанной в задаче, или установление связей между данными в условии задачи.

Алгоритм решения профессионально ориентированных математических задач, направленных на формирование креативного уровня квалификационного компонента профессиональной компетентности будущих инженеров, студентам не известен. Это предполагает выполнение студентами ранее усвоенных операций в новых ситуациях; требует от студента умения анализировать и использовать полученные знания в прикладных задачах, творчески применять знания и различные виды деятельности к новым объектам.

Приведем пример задачи, решение которой предполагает использование нескольких известных алгоритмов.

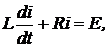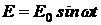Задача 3. Генератор газотурбинной энергоустановки работает на электрическую цепь. Сила тока в электрической цепи с омическим сопротивлением и коэффициентом самоиндукции удовлетворяет дифференциальному уравнению где – электродвижущая сила. Найти зависимость силы тока от времени, если изменяется по синусоидальному закону: и .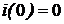

Для решения профессионально ориентированных задач, направленных на формирование креативного уровня квалификационного компонента профессиональной компетентности будущих инженеров, требуется определенная интуиция, творчество в выборе математического инструментария, интегрирование знаний из разных разделов курса математики, самостоятельная разработка алгоритма действий.

Предлагаемый комплекс профессионально ориентированных математических задач, направленный на формирование профессиональной компетентности будущих инженеров, отражает наиболее существенные процессы, явления, понятия технической сферы. Решая задачи различного уровня сложности, студенты оперируют профессиональными знаниями и умениями, приобретают умение анализировать ситуации.

Во втором параграфе описывается методика обучения студентов технических вузов решению профессионально ориентированных математических задач, строящаяся на лабораторном практикуме. В качестве примера взят раздел «Дифференциальные уравнения».

В приложениях математики к техническим наукам дифференциальные уравнения занимают особо важное место. Многие прикладные процессы с их помощью описываются проще и полнее. Дифференциальные уравнения дают возможность решать многие вопросы общетехнических и прикладных дисцип­лин: физики, теоретической механики, сопротивления материалов, гидравлики, теории машин и механизмов и т. д., часто сами возникают при решении этих во­просов.

В работе отмечается и обосновывается, что на лабораторных занятиях оп­тимальной является групповая форма обучения, при которой студентам предос­тавляется возможность для проявления личной активности. В условиях обяза­тельного совместного выполнения заданий партнеры поставлены перед необхо­димостью кооперировать свои усилия в достижении общей цели. Здесь прояв­ляется психологический фактор «вместе», способствующий преодолению не­уверенности в себе, особенно при затруднениях в выполнении задания, осозна­нию «общего фонда мыслей». Каждый студент при объяснении материала, его закреплении и контроле, оценке выполненных действий и заданий фактически выполняет функции преподавателя, то есть социально значимую деятельность, которая является важным звеном в формировании элементов организационно управленческой деятельности инженера.

С целью формирования профессиональной компетентности в условиях уровневой дифференциации лабораторное занятие организовывалось следую­щим образом: при общем задании для всех студентов, каждая группа, образо­ванная в соответствии с уровнем сформированности профессиональной компе­тентности, имела свою цель работы.

В качестве примера в работе приведен фрагмент организации лаборатор­ного занятия по теме «Обыкновенные дифференциальные уравнения».

Если студент находился на интуитивном уровне сформированности про­фессиональной компетентности, то цель работы «Решение с помощью про­граммной среды MATLAB профессионально ориентированных задач, математи­ческой моделью которых является обыкновенное дифференциальное уравне­ние» состояла в выработке навыков решения дифференциального уравнения с помощью MATLAB. Для студента, находящегося на нормативном уровне сфор­мированности профессиональной компетентности, цель этой же работы форму­лировалась следующим образом: выработать навыки составления математической модели технических систем в виде дифференциального уравнения и решить его с помощью MATLAB. Студент, находящийся на креативном уровне сформированности профессиональной компетентности, выполнял работу, целью которой было развитие способности критически оценивать полученные в процессе решения профессионально ориентированной математической задачи средствами MATLAB, результаты моделирования.

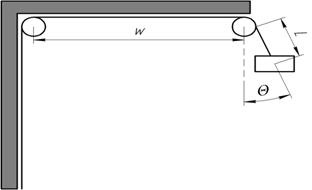
На лабораторном занятии студенты проектировали работу крана, используемого для погрузки морских контейнеров в порту, который схематически представлен на рисунке (рис. 3).

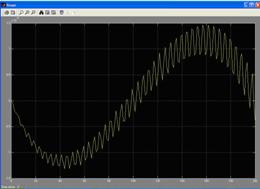
Студентам, находящимся на креативном уровне сформированности профессиональной компетентности, предлагалось варьировать ускорение крана, обеспечивая колебание троса меньшее, чем 1,5×10-4 рад. Оптимальную зависимость колебаний троса от времени студенты наблюдали на графике, изображенного средствами MATLAB (рис. 4).

На лабораторных занятиях студентам предлагалось как общее задание для всех, так и индивидуальные задания различных уровней сложности с учетом уровней сформированности профессиональной компетентности.

Так, при изучении темы «Обыкновенные дифференциальные уравнения первого порядка» три группы студентов выполняли следующие задания: Решить профессионально ориентированную математическую задачу средствами MATLAB:

·  Первый уровень сложности: «В транспортный цех установлен аварийный генератор, поддерживающий напряжение Е = 300 В. Сопротивление сети цеха R = 150 Ом, коэффициент самоиндукции L = 30 Гн. За какое время с момента включения генератора, ток i в сети достигнет 90% своей предельной величины».

·  Второй уровень сложности: «Аккумулятор АКТЕХ емкостью с=120 включается в цепь с напряжением E = 220 В и сопротивлением R = 5 Ом. Определить заряд q аккумулятора в момент t после включения».

·  Третий уровень сложности: «На цепь с сопротивлением R и самоиндукцией L работает асинхронный генератор, возбуждающий периодическую электродвижущую силу (где Т – период, t – время, а – постоянное число, равное максимальному значению величины ). Определить силу тока i в цепи в любой момент времени, если в начальной момент (t=0) сила тока равна нулю».

Группы студентов, образованные в соответствии с уровнем сформированности профессиональной компетентности, выполняли часть общего задания, после чего обсуждали полученные результаты. Так, например, при изучении темы «Неполные дифференциальные уравнения» рассматривалась задача: «Тягач массой P=15 т осуществляет буксировку груза, преодолевая сопротивление, равное , где , m – масса, а v – скорость буксировки. Сила тяги направлена по скорости в сторону движения и изменяется по закону: 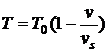, где T0=12 т – сила тяги без пробуксовки, а vs=const=5 км/час»; студентам предлагались задания:

-  для группы студентов, находящихся на интуитивном уровне сформированности профессиональной компетентности: «Найти зависимость скорости тягача от времени, если начальная скорость равна v0»;

-  для группы студентов, находящихся на нормативном уровне сформированности профессиональной компетентности: «Найти зависимость пройденного пути от времени»;

-  для группы студентов, находящихся на креативном уровне сформиро­ванности профессиональной компетентности: «Найти зависимость пути от вре­мени при начальной скорости v0=1 км/час».

Применение компьютерных математических пакетов не ограничивалось лишь демонстрацией иллюстраций в учебном процессе, а использовались те возможности, которые они предоставляют для выполнения различного рода учебных заданий.

В третьем параграфе описаны организация и результаты педагогического эксперимента, состоящего из трех этапов: констатирующего, поискового, формирующего.

Целями констатирующего эксперимента (2004–2005 гг.) являлись: обоснование актуальности исследования; выявление недостатков традиционной методики обучения математике студентов технических вузов; выявление роли и определение места профессионально ориентированных задач в реализации уровневой дифференциации; выбор методов исследования; выявление начального уровня сформированности профессиональной компетентности студентов первого курса факультета «Транспорта, нефти и газа» Омского государственного технического университета (ФТНГ ОмГТУ).

В начале педагогического эксперимента 61 студенту была предложена контрольная работа по математике с целью определения качества математической подготовки. Результаты контрольной работы обнаружили значительные пробелы в знаниях обучающихся и несформированность ряда умений и навыков (незнание определений ведущих понятий, незнание свойств понятий, незнание теорем, неумение подводить объект под понятие, неумение выполнять тождественные преобразования алгебраических и неалгебраических выражений, неумение решать различного рода уравнения, неравенства и их системы, неумение использовать дифференциальное и интегральное исчисления к решению прикладных сюжетных задач и др.). Было установлено, что причинами указанных негативных фактов являются: причины, обусловленные несовершенством программ и учебников по математике; причины, обусловленные несовершенством организации учебного процесса; причины, обусловленные несформированностью на должном уровне психических процессов (память, внимание, мышление и т. д.); причины, обусловленные невладением обучающимися синтаксисом и семантикой математического языка. Результаты контрольной работы представлены в таблице (табл.5):

Целями поискового эксперимента (2005–2007 гг.) являлись: разработка комплекса профессионально ориентированных задач; разработка методики применения профессионально ориентированных математических задач; определение критериев проверки уровня сформированности профессиональной

Таблица 5

Результаты констатирующего эксперимента

компетентности; формулирование гипотезы исследования.

Формирующий эксперимент проводился в 2007–2009 гг. Им было охва­чено 55 студентов ФТНГ ОмГТУ. На этом этапе эксперимента велось фор­мирование профессиональной компетентности студентов технических вузов средствами профессионально ориентированных математических задач в условиях уровневой дифференциации.

Цель педагогического эксперимента заключалась в проверке эффективности разработанной методики, которая должна быть выражена в повышении качества математической подготовки и в положительной динамике уровня сформированности профессиональной компетентности студентов технического вуза.

По окончании педагогического эксперимента студентам была предложена контрольная работа для определения качества их математической подготовки. Результаты эксперимента показали, что 27 % студентов получили отметку «5», 34 % – отметку «4», 25 % – отметку «3», 14 % – отметку «2».

Помимо качества математической подготовки студентов технических вузов в педагогическом эксперименте отслеживался и уровень сформированности профессиональной компетентности.

Для определения уровня сформированности профессиональной компетентности студентов составлены специальные контрольные работы, состоящие из 5 профессионально ориентированных математических задач и которые были предложены до и после проведения эксперимента. Оценка уровня сформированности квалификационного компонента профессиональной компетентности проводилась по сумме баллов, набранных за решения первых четырех задач контрольной работы, каждая из которых оценивалась от 1 до 5 баллов. Оценка уровня сформированности психологического компонента профессиональной компетентности проводилась по результатам решения четырех первых задач контрольной работы. Для оценки уровня сформированности социального компонента профессиональной компетентности была организована групповая работа студентов по решению профессионально ориентированной задачи (в контрольной работе это задача 5). В ходе исследования при оценивании психологического и социального компонентов использовался метод наблюдения. Данные наблюдений заносились в таблицу, в которой отмечались основные характеристики:

−  психологический компонент: студент использует различные подходы к решению задач; студент проявляет внимательность при решении задач; студент проявляет аккуратность при оформлении решения задач; студент пытается решить задачу более высокого уровня сложности; студент проявляет творческий подход к решению задач;

−  социальный компонент: студент участвует в обсуждении решения предложенной задачи; студент отстаивает свою точку зрения при решении задачи; студент предлагает несколько идей решения задачи; студент организует работу по решению задачи в группе; студент осуществляет взаимопомощь и взаимоконтроль.

За каждую характеристику психологического компонента студент мог получить до 1 балла (за каждую характеристику по 0,25 балла), тем самым набрать в сумме до 5 баллов. Социальный компонент оценивался по указанным характеристикам, за каждую из которых выставлялось по 1 баллу.

На диаграммах (рис. 5) отражена положительная динамика уровня сформированности компонентов профессиональной компетентности будущих инженеров (квалификационный, психологический и социальный).

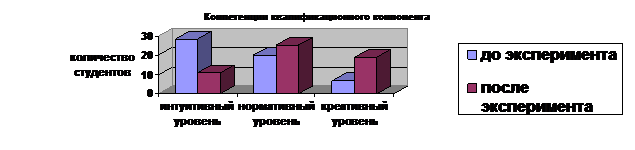
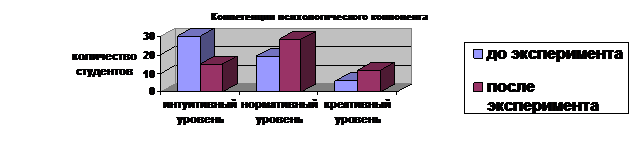
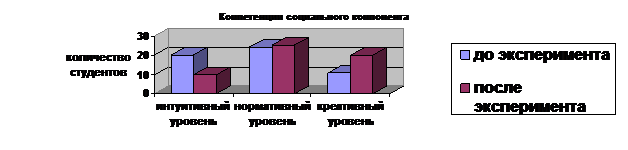
Рис. 5. Динамика сформированности профессиональной компетентности

Для проверки эффективности разработанной методики, способствующей формированию профессиональной компетентности, использовался критерий знаков (данные представлены в таблице 6), на основе которого был сделан вывод о том, что уровень сформированности профессиональной компетентности студентов повысился в результате применения разработанной методики.

Таблица 6

Данные эксперимента по критерию знаков

Результаты свидетельствуют о том, что предложенная методика оказывает статистически значимое влияние на процесс формирования профессиональной компетентности студентов технических вузов.

В заключении приведены результаты, полученные в ходе работы над диссертацией, и сделаны общие выводы:

1. Определены психолого-педагогические основы профессиональной подготовки студентов технических вузов при обучении математике в условиях компетентностного подхода. Показана многоаспектность компетентностного подхода в решении проблемы математической подготовки, способствующей формированию профессиональной компетентности будущих инженеров. В рамках данного исследования «профессиональная компетентность» понимается как интегральная характеристика личности специалиста, представляемая комплексом компетенций в профессиональной сфере деятельности, включающей его личностное отношение к ней и ее предмету. Определены психологический, квалификационный, социальный компоненты профессиональной компетентности.

2. Выявлена роль и определено место профессионально ориентированных математических задач в формировании профессиональной компетентности студентов технических вузов.

3. Разработана структурно-функциональная модель процесса формирова­ния квалификационного, психологического и социального компонентов профессиональной компетентности будущих инженеров в процессе обучения решению профессионально ориентированных математических задач, определены направления ее реализации в условиях уровневой дифференциации.

4. В диссертации разработан комплекс профессионально ориентирован­ных математических задач, обеспечивающий сопровождение процесса формирования профессиональной компетентности будущих инженеров.

5. Разработана методика обучения математике студентов транспортных и нефтегазовых направлений технических вузов на основе использования выде­ленного комплекса профессионально ориентированных математических задач и лабораторного практикума, способствующего формированию профессиональ­ной компетентности студентов в условиях уровневой дифференциации. Прове­ден педагогический эксперимент, результаты которого свидетельствуют о по­вышении качества математической подготовки студентов, и подтвердивший эффективность разработанной методики, способствующей формированию про­фессиональной компетентности студентов технического вуза.

Таким образом, поставленные задачи исследования решены в полном объеме и гипотеза исследования доказана.

Дальнейшее решение исследуемой проблемы может быть продолжено в плане изучения возможностей связи математики с дисциплинами обще­образовательного, общетехнического и профессионального циклов для реали­зации как профессионально ориентированного обучения математике, так и не­прерывной математической подготовки в процессе обучения студентов инженерных специальностей.

Основные положения и результаты диссертационного исследования отражены в следующих публикациях:

Публикации в научных журналах и изданиях, рекомендованных ВАК РФ:

1.  Федотова, Т. И. (Бова Т. И.) О роли самостоятельной работы в формировании профессиональной компетентности будущего специалиста / // Омский научный вестник– № 1. – С. 182 – 184.

2.  Федотова, Т. И. (Бова Т. И.) Задачи как средство формирования профессиональной компетентности будущих инженеров в процессе обучения математике / // Омский научный вестник– № 3. – С. 123 – 125.

3.  Федотова,  организации процесса обучения математике в техническом вузе, направленного на формирование профессиональной компетентности будущего инженера / // Омский научный вестник– № 3. – С. 183–185.

4.  Федотова, Т. И. (Бова Т. И.) Профессиональная компетентность как основополагающий компонент подготовки будущего инженера / // Приложение к журналу Омский научный вестник– № 9. – С. 65–69.

Учебно-методические издания:

5.  Федотова,  ориентированные задачи по математике для студентов инженерных специальностей: Учебное пособие / . – Омск: «Сфера», 2009. – 104 с.

Научные статьи и материалы выступлений на конференциях:

6.  Федотова, Т. И. (Бова Т. И.) К вопросу о квалификационной и компетентностной моделях специалиста / , // Наука и молодежь. Материалы VIII Всероссийской научно-практической конференции студентов, соискателей, молодых ученых и специалистов (24 мая 2007). – Н. Новгород: Изд-во ВГИПУ, 2007. – Т.1. – С. 9 – 10. (авт. 50 %).

7.  Федотова, Т. И. (Бова Т. И.) Математическое образование инженера / // Современная математика и математическое образование в вузах и школах России: опыт, тенденции, проблемы. Межвузовский сборник научно-методических работ. – Вологда: Изд-во «Русь», ВГПУ, 2006. – С. 58 – 60.

8.  Федотова,  дифференцированного урока математики / // Учитель в современных моделях обучения. Материалы конференции 26-28 марта 2002 г. – Томск: Изд-во Том. Ун-та, 2002. – С. 101 – 102.

9.  Федотова, Т. И. (Бова Т. И.) О математическом моделировании в процессе подготовки будущих инженеров / // Молодежь, наука, творчество – 2007. Межвузовская научно-практическая конференция студентов и аспирантов: сборник материалов / Под общ. ред. . – Омск: Изд-во ОГИС, 2007. – С. 53 – 54.

10.  Федотова, Т. И. (Бова Т. И.) О реализации уровневой дифференциации обучения математическим дисциплинам в ВТУЗах / // Математическое образование: концепции, методики, технологии. Сборник трудов по материалам III международной научной конференции «Математика. Образование. Культура»,17–21 апреля 2007 г. – Тольятти: Изд-во ТГУ, 2007. – Ч.3. – С. 288 – 293.

11.  Федотова, Т. И. О роли математического образования в формировании профессиональной компетентности будущего инженера / // Вестник развития науки и образования. – М.: Изд-во «Наука», 2009. – № 3. – С. 88 – 89.

12.  Федотова, Т. И. (Бова Т. И.) О роли самостоятельной работы при обучении математике будущих инженеров в контексте формирования профессиональной компетентности / // Актуальные вопросы методики преподавания математики и информатики. Сборник научных трудов Второй Всероссийской научно-практической конференции, 16 апреля 2007 г. – Биробиджан: Изд-во ДВГСГА, 2007. – С. 18 – 20.

13.  Федотова, Т. И. (Бова Т. И.) Профессионально ориентированные задачи по математике как средство формирования профессиональной компетентности будущих инженеров / // Альманах современной науки и образования. – Тамбов: «Грамота», 2008. – №1(8): Математика, физика, строительство, архитектура, технические науки и методика их преподавания. – С. 17 – 18.

14.  Федотова, Т. И. (Бова Т. И.) Уровневая дифференциация обучения математики студентов технических вузов / // Современные проблемы математического и физического образования в школе и вузе. Сборник трудов Всероссийской научно-практической конференции, 9–10 октября 2006 г. – Стерлитамак: Изд-во СГПА, 2006. – С. 14 – 17.