Федеральное агентство по образованию

ГОУ ВПО «УГТУ-УПИ имени первого Президента России »

Институт образовательных информационных технологий

Факультет дистанционного образования

Кафедра ___________________________________

Курсовая работа

по Теории информационных процессов и систем № 1

(ДИСЦИПЛИНА)

на тему: Задачи сетевого планирования и управления

Вариант № 17

Семестр № 7

Преподаватель

( ФИО)

Студент гр. № ИТЗ-46011д

(ФИО)

номер зачетной книжки 18604311

Екатеринбург

2009

Курсовая работа по Теории информационных процессов и систем №

(ДИСЦИПЛИНА)

№ записи в книге регистрации дата регистрации 2009 г.

Преподаватель

(ФИО)

Студент группа № ИТЗ-46011д

(ФИО)

Деканат ФДО

Содержание

Введение 3

1. Сетевое планирование и управление 4

1.1 Назначение и область применения 4

1.2 Сетевая модель и ее основные элементы 4-7

1.3 Правила построения сетевых графиков 7-11

2. Решение задачи 12

Заключение 16

Список используемой литературы 17

Введение

Методы сетевого планирования и управления (СПУ), разработан­ные в начале 50-х годов, широко и успешно применяются для оптими­зации планирования и управления сложными разветвленными комплек­сами работ, требующими участия большого числа исполнителей и зат­рат ограниченных ресурсов.

Выполнение комплексных научных исследований, а также проектирование и строительство промышленных, сельскохозяйственных и транспортных объектов требуют календарной увязки большого числа взаимосвязанных работ, выполняемых различными организациями. Составление и анализ соответствующих календарных планов представляют собой весьма сложную задачу, при решении которой применяются так называемые методы сетевого планирования. По существу, этот метод дает возможность определить, во-первых, какие работы или операции из числа многих, составляющих проект, являются «критическими» по своему влиянию на общую календарную продолжительность проекта и, во-вторых, каким образом построить наилучший календарный план проведения всех работ по данному проекту с тем, чтобы выдержать заданные сроки при минимальных затратах.

Модели сетевого планирования и управления (модели СПУ) предназначены для планирования и управления сложными комплексами работ (проектами), направленными на достижение определенной цели в заданные сроки (строительство, разработка и производство сложных объектов и др.).

Сетевой моделью (СМ) называется экономико-математическая модель, отражающая весь комплекс работ и событий, связанных с реализацией проекта в их логической и технологической последовательности и связи.

В СПУ применяются связные, ориентированные графы без циклов, имеющие одну начальную и одну конечную вершин.

1. Сетевое планирование и управление

1.1  Назначение и область применения

Сетевое планирование – это комплекс графических и расчетных методов организационных мероприятий, обеспечивающих моделирование, анализ и динамическую перестройку плана выполнения сложных проектов и разработок, например, таких как:

·  строительство и реконструкция каких-либо объектов;

·  выполнение научно-исследовательских и конструкторских работ;

·  подготовка производства к выпуску продукции;

·  перевооружение армии.

Характерной особенностью таких проектов является то, что они состоят из ряда отдельных, элементарных работ. Они обусловливают друг друга так, что выполнение некоторых работ не может быть начато раньше, чем завершены некоторые другие.

1.2 Сетевая модель и её основные элементы

Основными понятиями сетевых моделей являются понятия события, работы и пути. Построение сетевой модели (структурное планирование) начинается с разбиения проекта на четко определенные работы, для которых определяется продолжительность.

Работа-это некоторый процесс, приводящий к достижению определенного результата, требующий затрат каких-либо ресурсов и имеющий протяженность во времени.

По своей физической природе работы можно рассматривать как:

·  действие (заливка фундамента бетоном, составление заявки на материалы, изучение конъюнктуры рынка);

·  процесс (старение отливок, выдерживание вина, травление плат);

·  ожидание (ожидание поставки комплектующих, прослеживание детали в очереди к станку).

По количеству затрачиваемого времени работа может быть:

·  действительной, т. е. требующей затрат времени;

·  фиктивной, т. е. формально не требующей затрат времени и представляющей связь между какими-либо работами (передача измененных чертежей от конструкторов к технологам, сдача отчета о технико-экономических показателях работы цеха вышестоящему подразделению).

Фиктивная работа может реально существовать, например, "передача документов от одного отдела к другому". Если продолжительность такой работы несоизмеримо мала по сравнению с продолжительностью других работ проекта, то формально ее принимают равной 0. Существуют фиктивные работы, которым в реальности не соответствуют никакие действия. Такие фиктивные работы только представляют связь между другими работами сетевой модели. Работы связаны друг с другом таким образом, что выполнение одних работ может быть начато только после завершения некоторых других.

Событие – момент времени, когда завершаются одни работы и начинаются другие. Событие представляет собой результат проведенных работ и в отличие от работ не имеет протяженности во времени. Например, фундамент залит бетоном, старение отливок завершено, комплектующие поставлены, отчеты сданы и т. д.

Таким образом, начало, и окончание любой работы описываются парой событий, которые называются начальным и конечным событиями. Поэтому для идентификации конкретной работы используют код работы (ij), состоящий из номеров начального (i-ro) и конечного (j-ro) событий, например 2-4; 3-8; 9-10.

На этапе структурного планирования взаимосвязь работ и событий изображается с помощью сетевого графика, где работы изображаются стрелками, которые соединяют вершины, изображающие события. Около каждой стрелки ставится среднее время выполнения соответствующей работы. Любое событие может считаться наступившим только тогда, когда закончатся все входящие в него работы. Поэтому работы, выходящие из некоторого события не могут начаться, пока не будут завершены все операции, входящие в это событие.

работа i,j

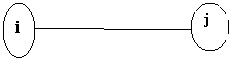Рис. 1.1 – Кодирование работы

Номер исходного события равен единице. Номера остальных событий соответствуют последней цифре кода предшествующей данному событию работы (или работ).

Событие, не имеющее предшествующих ему событий, т. е. с которого начинается проект, называют исходным событием. Событие, которое не имеет последующих событий и отражает конечную цель проекта, называется завершающим. Событие, характеризующее собой факт окончания всех предшествующих работ и начало всех последующих работ, называется промежуточным или просто событием.

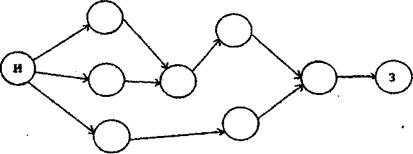
Рис. 1.2

Важное значение для анализа сетевых моделей имеет понятие пути.

Путь – это любая последовательность работ в сетевом графике (в частном случае это одна работа), в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы. Различают следующие виды путей:

Полный путь – это путь от исходного до завершающего события. Критический путь – максимальный по продолжительности полный путь. Подкритический путь – полный путь, ближайший по длительности к критическому пути.

Работы, лежащие на критическом пути, называют критическими. Каждый путь характеризуется своей продолжительностью (длительностью), которая равна сумме продолжительностей составляющих его работ.

1.3  Правила построения сетевых графиков

При построении сетевого графика необходимо следовать следующим правилам:

- длина стрелки не зависит от времени выполнения работы;

- стрелка не обязательно должна представлять прямолинейный отрезок;

- для действительных работ используются сплошные, а для фиктивных – пунктирные стрелки;

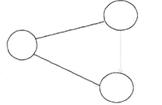
- каждая операция должна быть представлена только одной стрелкой;

- не должно быть параллельных работ между одними и теми же событиями, для избежания такой ситуации используют фиктивные работы;

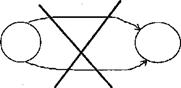
- следует избегать пересечения стрелок;

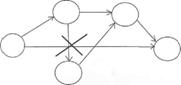
- не должно быть стрелок, направленных справа налево;

- номер начального события должен быть меньше номера конечного события;

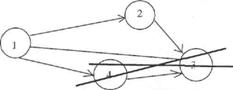
- не должно быть висячих событий (т. е. не имеющих предшествующих событий), кроме исходного;

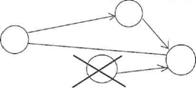
- не должно быть тупиковых событий (т. е. не имеющих последующих событий), кроме завершающего;

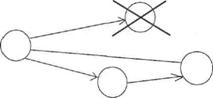
- не должно быть циклов;

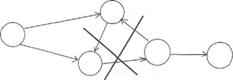
Сетевой график включает в себя работы и события.

Работы на сетевом графике обозначаются стрелками, около которых ставится среднее время выполнения соответствующей работы.

При построении сетевого графика имеют место следующие события:

·  исходное событие – это событие, в отношении которого предполагается, что оно не имеет предшествующей работы;

·  завершающее событие – это событие, в отношении которого предполагается, что оно не имеет последующих работ;

·  промежуточное или просто событие – это событие, характеризующее собой факт окончания всех предшествующих работ и начало всех последующих работ.

Событие обозначается кружком, который содержит следующую информацию:

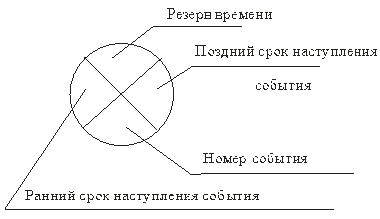
Номер исходного события равен единице. Номера остальных событий соответствуют последней цифре кода предшествующей данному событию работы (или работ).

При построении сетевого графика должна соблюдаться существующая очерёдность выполнения работ.

Для определения средних значений резервов времени по отдельным событиям определяются средние значения ранних и поздних сроков событий начала и окончания работ.

Путём в сетевом графике называется любая последовательность работ (стрелок), связывающая какие-либо два события. При этом пути, связывающие исходное и завершающее события сети, считаются полными, а все другие пути – неполными. Каждый путь характеризуется своей продолжительностью (длительностью), которая равна сумме продолжительностей составляющих его работ.

Наиболее простым и наглядным методом расчёта параметров сети является графический. Кружки-события заполняются в следующем порядке:

В нижний сектор ставится порядковый номер события.

Путём последовательного перехода от исходного события, ранний срок свершения которого равен нулю, к завершающему событию рассчитываются ранние сроки его свершения. Ранний срок наступления события представляет собой минимальный из возможных моментов наступления должного события при заданной продолжительности работ и начальном моменте.

Ранний срок наступления j-го события вычисляется по формуле:

, i =1,…,к,

где (i =1,…,к) – ранний срок наступления i-го события;

(i =1,…,к) – средняя продолжительность работы ij;

к – число работ, непосредственно предшествующих j-му событию.

Ранние сроки определяются величиной наиболее длительного отрезка пути от исходного события до рассматриваемого.

Путём последовательного перехода от завершающего события, поздний срок которого равен величине критического пути, рассчитывают поздний срок его свершения. Этот срок определяется разностью продолжительности критического пути и максимальным из путей, следующим за этим событием.

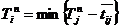, j =1,…,,

где (j=1,…,) – поздний срок наступления j-го события;

– число работ, непосредственно следующих за i-м событием (все эти работы на сетевом графике обозначаются стрелками, выходящими из кружка, обозначающего i-ое событие).

Поздний срок наступления завершающего события принимается равным раннему сроку наступления того же события.

Разность между поздним и ранним сроками свершения событий – есть резерв времени этого события. Резерв времени i-го события вычисляется по формуле:

.

После вычисления резервов времени определяется критический путь , то есть полный путь, имеющий наибольшую продолжительность. Для него является характерным, что все события, принадлежащие ему, не имеют резервов времени (они равны нулю).

Полный резерв времени работы, представляющий собой максимальное время, на которое можно увеличить продолжительность работы (не изменяя длительности критического пути), определяется как разность между поздним сроком свершения события, завершающего работу, и ранним сроком свершения предшествующего работе события минус продолжительность самой работы.

2. Решение задачи

На предприятии осуществляется реконструкция цеха. Известна средняя продолжительность выполнения отдельных работ (таблица 1.1). Среднеквадратическое отклонение продолжительности выполнения работ по всем работам равно одному дню.

Необходимо:

1.  Построить сетевой график по выполнению работ по реконструкции цеха и определить значение его параметров (ранние и поздние сроки наступления событий, начала и окончания работ, резервы времени по отдельным событиям).

2.  Определить на сетевом графике критический путь, дать перечень работ, принадлежащих к критическому пути и его длительность. На сетевом графике выделить критический путь.

Таблица 1.1

Определяем ранние сроки наступления j-го события сетевого графика:

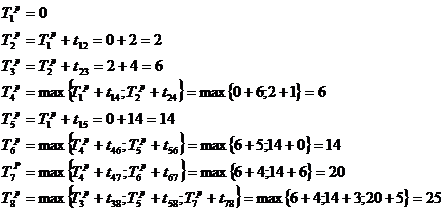
Определяем поздние сроки свершения i - го события :

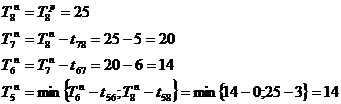
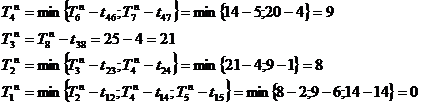
Определим резерв времени i-го события сетевого графика.

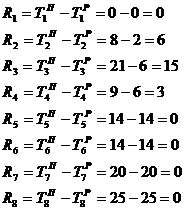
Определим критический путь сетевого графика , т. е. полный путь, имеющий наибольшую продолжительность и характеризующийся тем, что все принадлежности ему события не имеют резервов времени (они равны нулю).

Рассмотрим все пути, проходящие через вершины сетевого графика с нулевыми резервами времени:

1) . Его продолжительность равна:

(дней).

2) 1-5-8. Его продолжительность равна:

(дней).

Таким образом, критическим путем является путь и его продолжительность составляет 25 дней.

Перечень работ, принадлежащих критическому пути, представлен в таблице 1.2.

Таблица 1.2

Найдём полный резерв времени работ.

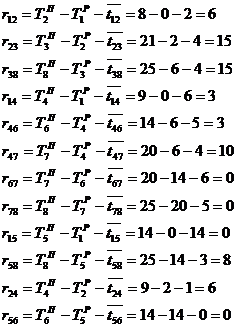
Сетевой график выполнения работ по реконструкции цеха представлен на рисунке 1.3.

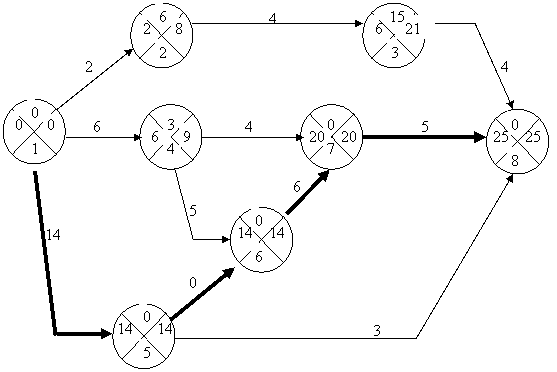
Рисунок 1.3

Ответ: Таким образом, критический путем является путь и его длительность (продолжительность) составляет 25 дней.

ЗАКЛЮЧЕНИЕ

Модели сетевого планирования и управления (модели СПУ) предназначены для планирования и управления сложными комплексами работ (проектами), направленными на достижение определенной цели в заданные сроки (строительство, разработка и производство сложных объектов и др.).

В СПУ применяются связные, ориентированные графы без циклов, имеющие одну начальную и одну конечную вершин.

Выполнение комплексных научных исследований, а также проектирование и строительство промышленных, сельскохозяйственных и транспортных объектов требуют календарной увязки большого числа взаимосвязанных работ, выполняемых различными организациями. Составление и анализ соответствующих календарных планов представляют собой весьма сложную задачу, при решении которой применяются так называемые методы сетевого планирования. По существу, этот метод дает возможность определить, во-первых, какие работы или операции из числа многих, составляющих проект, являются «критическими» по своему влиянию на общую календарную продолжительность проекта и, во-вторых, каким образом построить наилучший календарный план проведения всех работ по данному проекту с тем, чтобы выдержать заданные сроки при минимальных затратах.

В ходе выполнения курсового проекта был построен сетевой график, по реконструкции цеха и определено значение его параметров (ранние и поздние сроки наступления событий, начала и окончания работ, резервы времени по отдельным событиям).

Определи критический путь сетевого графика , т. е. полный путь, имеющий наибольшую продолжительность и характеризующийся тем, что все принадлежности ему события не имеют резервов времени (они равны нулю). Критическим путем является путь и его продолжительность составляет 25 дней.

Список используемой литературы

1.  , , Математические методы сетевого планирования, М., 1965;

2.  Модер Дж., Метод сетевого планирования в организации работ, пер. с англ., М. — Л., 1966.

3.  Основные положения по разработке и применению систем сетевого планирования и управления, 2 изд., М., 1967;

4.  Сетевые графики в планировании, М., 1967;

5.  Сетевые модели и задачи управления, М., 1967;

6.  Таха Введение в исследование операций, 7 изд., М., 2005