Домашнее задание на летние каникулы (после 6 класса)
Решения заданий должны быть выполнены в отдельной (лучше – общей, не менее 48 листов) тетради. Можно использовать тетрадь для домашних заданий, оставшуюся с прошлого года.
Все вычисления необходимо записывать в тетрадь. Отсутствие вычислений – основание для снижения оценки (вплоть до неудовлетворительной).
Убедительная просьба решения всех заданий записывать по порядку, не забывая про нумерацию. В случае несоблюдения этого требования проверки решений придётся ждать очень долго!
Тетрадь с решениями должна быть сдана на первом уроке алгебры в новом учебном году.
Основная часть
1. а) Обратите все указанные обыкновенные дроби в десятичные: 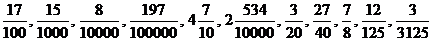 .
.
б) Найдите сумму и произведение наибольшей и наименьшей из них.
в) Приведите три примера дробей, которые нельзя записать в виде конечной десятичной дроби. Объясните, по какому принципу вы подбирали эти дроби. Запишите их в виде периодических дробей, затем округлите их до тысячных.
2. Разложите числа на простые множи, 28000, 63063, 16632.
3. Найдите наибольший общий делитель и наименьшее общее кратное чисел:
а) 12 и 16; б) 25 и 48; в) 140 и 35; г) 24 и 16; д) 900 и 36.
4. Вычислите (если возникают затруднения, выполняйте примеры по действиям, указывая их порядок):
а) 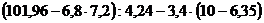 ;
;
б) 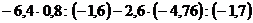 ;
;
в) 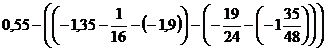 ;
;
г) 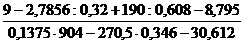 .
.
5. а) Отметьте на координатной плоскости следующие точки и соедините их по порядку:
(0; 4), (2; 8), (6; 10), (9; 7), (9; 4), (7; 2), (7; 0), (6; 2), (6; –1), (5; 1), (5; –2), (4; 0), (3; –2), (2; 0),
(1; –1), (–1; –2), (0; –3), (–1; –3), (–1,5; –4), (0; –4), (–4; –6), (–3; –5), (–5; –5), (–3; –4,5), (–5; –4),
(–2; –4), (–2; –1), (–6; 2), (–7; 4), (–8; 4), (–7; 6), (–8; 5), (–9; 6), (–7; 7), (–9; 9), (–7; 8), (–8; 11),
(–6; 9), (–5; 10), (–5; 9), (–4; 10), (–4; 9), (–3; 9), (–4; 8), (–3; 7), (–4; 7), (–4; 6), (–5; 7), (–5; 6),
(–3; 4), (0; 4).
б) Озаглавьте полученную картинку.
в) Добавьте ещё одну точку, необходимую для завершения картинки, и запишите её координаты.
6. Составьте буквенное выражение для решения задачи.
В магазин привезли а ящиков яблок по 25 кг в каждом и b ящиков апельсинов по 20 кг в каждом. Сколько килограммов фруктов привезли в магазин?
7. В первый день было вспахано 14,25 га, что на 3,6 га больше, чем во второй день, и на 4,15 га меньше, чем в третий день. Сколько гектаров было вспахано за эти три дня?
8. Вычислите удобным способом и поясните свои вычисления:
а) 3,452+17,23+1,548; б) ![]() ;
;
в) 54271+39999+10001; г) 56+56+56+56+56+74+740+740;
д) 9,835–4,95–2,835; е) 3+137+444+873+556+997;
ж) 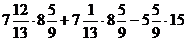 ; з)
; з) ![]() .
.
9. Из ![]() части собранной вишни сварили варенье, а из
части собранной вишни сварили варенье, а из ![]() оставшейся части сделали компот.
оставшейся части сделали компот.
Какая часть вишни была использована на компот?
10. Решите уравнение: а) 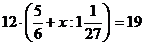 ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) 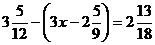 ; е)
; е) ![]() ;
;
ж) ![]() ; з)
; з) 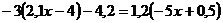 .
.
11. Являются ли взаимно обратными значения выражений: ![]() и
и ![]() . Объясните, почему.
. Объясните, почему.
12. В первый день было скошено ![]() луга, а во второй –
луга, а во второй – ![]() остатка. Площадь нескошенной части равна 15 га. Какова площадь всего луга? Ответ запишите в квадратных метрах.
остатка. Площадь нескошенной части равна 15 га. Какова площадь всего луга? Ответ запишите в квадратных метрах.
13. Какова скорость парохода (в км/час), если он проплывает 25 км за 35 минут?
14. Радиус окружности, длина которой равна 138,16 см увеличили на 5 см. На сколько увеличилась длина этой окружности?
15. 10 мартышек съедят коробку бананов за 18 минут. Сколько ещё нужно позвать мартышек, чтобы они управились с бананами за 12 минут?
16. Некоторый товар стоил 800 рублей. Его цена сначала понизилась на 15%, а затем повысилась на 16%. Как изменилась цена товара и на сколько?
17. Если к задуманному числу прибавить 7 и полученную сумму увеличить втрое, то получится –6. Найдите задуманное число.
18. В подъезде жилого дома 8 однокомнатных квартир, 7 – двухкомнатных и 5 – трёхкомнатных. Постройте по этим данным круговую и столбчатую диаграммы.
19. Решите задачу с помощью уравнения.
С первого участка собрали в 2 раза больше картофеля, чем со второго и на 230 ц больше,
чем с третьего. С какого из двух участков, второго или третьего, собрано больше и на сколько, если всего с трёх участков собрали 720 ц?
20. Отметьте на координатной прямой все числа, кратные 3, модули которых меньше 20, но больше 11.
21. Сколько килограммов песка вмещает ящик, если его длина 1,2 м, ширина составляет ![]() длины, а высота – 0,55 ширины? 1 м3 песка весит
длины, а высота – 0,55 ширины? 1 м3 песка весит ![]() т.
т.
22. Какой процент составляют:
а) 420 кг от 15 т; б) 32,25 км от 215 км; в) 36 л от 14,4 л; г) 4,4 руб от 320 руб?
23. Запишите в тетради, что называется масштабом карты. Решите следующие задачи по теме «Масштаб».
а) Расстояние между двумя точками на карте – 6 см. Найдите расстояние между этими точками на местности, если масштаб карты 1:250000.
б) Найдите масштаб карты, если расстоянию в 350 км на местности соответствует отрезок на карте длиной в 1,4 см.
в) Изобразите в масштабе 1:300 отрезок длиной в 9 м.
24. Три бригады дорожных строителей установили 122 фонаря для освещения трассы. Первая бригада установила на 47 фонарей больше, чем вторая, а третья на 24 фонаря меньше, чем вторая. Сколько фонарей установила каждая бригада?
25. Найдите отношение площадей пола и постеленного на него ковра, если размеры пола 10 м×7 м, а размеры ковра 2,8 м×2 м? Что показывает это отношение?
Дополнительная часть
1. В бублике одна дырка, а в крендельке дырок в 2 раза больше. На сколько дырок больше в 9 крендельках, чем в 7 бубликах?
2. Трое рыбаков поймали 75 окуней и стали варить уху. Когда один дал 8 окуней, другой – 12, а третий – 7, то окуней у них осталось поровну. Сколько окуней поймал первый рыбак?
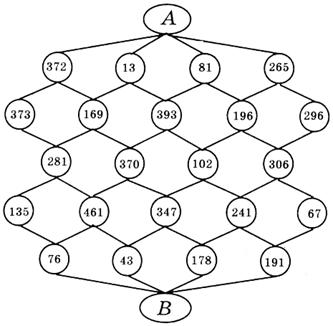
3. Среди множества дорог от А до В выберите ту, пройдя по которой вы сможете набрать ровно тысячу очков. Ответ запишите в виде примера на сложение.
4. Разрежьте каждую из фигур на одинаковые по форме части:
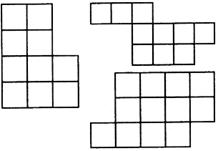
Чертежи приведите в тетради.
5. Для зоомагазина закупили 240 попугайчиков, причём синих втрое меньше, чем зелёных, а жёлтых столько, сколько синих и зелёных вместе. Сколько попугайчиков каждого цвета закупили?
6. Когда из ![]() числа вычли его 42%, то получили 273. Найдите это число.
числа вычли его 42%, то получили 273. Найдите это число.
7. Груз из контейнера можно перевезти на 8 грузовых машинах или на 12 прицепах. Сколько рейсов совершит машина с прицепом, чтобы перевезти груз из 15 таких контейнеров?
8. Первая бригада может выполнить работы по ремонту водопровода за 5 дней, а вторая – в ![]() раза быстрее. Смогут ли они отремонтировать водопровод за 3 дня, если будут работать вместе?
раза быстрее. Смогут ли они отремонтировать водопровод за 3 дня, если будут работать вместе?
9. Решите уравнение: 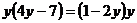 .
.
10. Некоторое число сначала уменьшили на 10%, а затем полученный результат увеличили на 40%. В результате получили 189. Чему равно исходное число?
11. Сократите дробь наиболее простым способом: ![]() .
.
12. Докажите, что 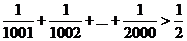 .
.
13. Моему брату через 2 года будет вдвое больше лет, чем ему было 2 года назад, а моя двоюродная сестра через 3 года будет вдвое старше, чем три года назад. Кто из них старше?
14. Теплоход прошёл 9 км по озеру и 20 км по течению реки за час. Какова скорость теплохода, если скорость течения реки – 3 км/ч?
15. В двух сосудах находится по 540 л воды. Из одного сосуда вытекает 25 л в минуту, а из другого – 15 л. Через сколько минут в одном из сосудов останется в шесть раз меньше воды, чем в другом?
Просьба сообщать о замеченных опечатках!




