![]() .
.
Отсюда найдем начальную скорость:
![]() .
.
Проверка размерности:
![]() .
.
Проведем вычисления:
![]()
Ответ: ![]()
![]() .
.
9) Задача на вращательное движение.
Диск массой m = 2 кг катится без скольжения по горизонтальной плоскости со скоростью v = 4 м/с. Найти кинетическую энергию диска.
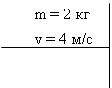 Дано: Решение:
Дано: Решение:
|
поступательного и вращательного движения:
Wк=Wпост + Wвращ (1)
При поступательном движении кинетическая энергия тела 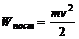 . (2)
. (2)
При вращательном движении 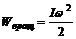 , (3)
, (3)
где 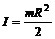 (4) – момент инерции диска,
(4) – момент инерции диска,
![]() (5) – угловая скорость вращения.
(5) – угловая скорость вращения.
Подставим выражения (4) и (5) в (3), получим
![]() (6).
(6).
Подставив формулы (6) и (2) в (1), окончательно получим:
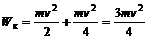 .
.
Вычислим искомую величину:
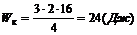 .
.
Вывод размерности:
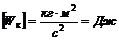 .
.
Ответ: Wк = 24 Дж.
10). Задача на колебания.
Точка совершает гармонические колебания согласно уравнению x = 0,4 sinπt (м). Определить скорость и ускорение точки через 1/6 c от начала колебаний.
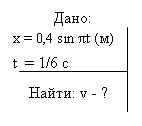 Решение.
Решение.
Запишем уравнение гармонических колебаний в общем виде:
x = A sin ωt, (1)
где x – смещение точки;
А – амплитуда; ω – круговая частота; t – время.
По определению, скорость равна производной от смещения по времени:
![]() . (2)
. (2)
Подставив (1) в (2), продифференцируем полученное выражение:
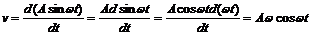 . (3)
. (3)
По определению, ускорение равно производной от скорости по времени:
![]() . (4)
. (4)
Подставив (3) в (4), продифференцируем полученное выражение:
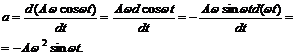 (5)
(5)
Из сравнения уравнения x = 0,1 sin πt и формулы (1) видно, что А = 0,1 м, ω = π с-1. По формулам (3) и (5) вычислим скорость и ускорение:
v = 0,1π cos πt, a = 0,1π2 sin πt. (6)
Проверим формулы (6), подставив единицы измерения:
[v] = м∙с-1 = м/с, [a] = м∙(с-1)2 = м/с2.
Вычислим искомые скорость и ускорение точки:
v = 0,4∙3,14 cos(π/6) = 1,091 м/с,
а = − 0,4∙3,142 sin (π/6) = −1,971 м/c2.
Ответ: v = 1,088 м/с, а = −1,971 м/c2.
11). Задача на явления переноса.
Определить, при каком градиенте плотности углекислого газа через каждый квадратный метр поверхности почвы продиффундирует в атмосферу в течение 1 ч масса газа m = 720 мг, если коэффициент диффузии D = 0,04 см2/с.

|
где D – коэффициент диффузии; ![]() – градиент плотности, т. е. изменение плотности, приходящееся на 1 м толщины слоя почвы; t – длительность диффузии.
– градиент плотности, т. е. изменение плотности, приходящееся на 1 м толщины слоя почвы; t – длительность диффузии.
Из (1) выразим искомый градиент плотности:
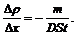 (2)
(2)
Проверим формулу (2), подставив единицы измерения
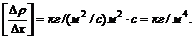
Вычислим градиент плотности:
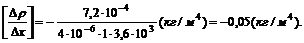
Отрицательное значение градиента плотности соответствует тому, что диффузия происходит в направлении убывания плотности вещества.
Ответ: ![]() = − 0,05 кг/м4.
= − 0,05 кг/м4.
12). Задача на I начало термодинамики.
Водород массой m = 200 г расширяется изобарически под давлением p = 3∙105 Па, поглощая в процессе расширения теплоту Q = 20 кДж. Определить работу расширения газа.
 Дано: СИ Решение:
Дано: СИ Решение:
Работа, совершаемая газом при неизменном давлении, выражается формулой
А = p(V2-V1) (1) Из уравнения Менделеева-Клапейрона, записанного
для начального и конечного состояний газа (рV1=mRT1/μ, pV2=mRT2/μ) выразим неизвестные начальный V1 и конечный V2 объемы
V1= mRT1/(pμ ); (2)
V2= mRT2/(pμ
Подставив (2) и (3) в (1), получим
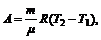 (4)
(4)
где μ – молярная масса водорода, R = 8,31 Дж/(К∙моль) – молярная газовая постоянная; Т1 и Т2 – начальная и конечная температуры газа.
Из формулы для теплоты при изобарическом процессе
Q = mcp(T2 − T1),
где ср – удельная теплоемкость газа при постоянном давлении, выразим неизвестную разность температур:
Т2 − Т1 = Q/(mcp). (5)
Известно, что
ср = (i + 2) R/(2μ), (6)
где i – число степеней свободы молекулы газа. Подставив (6) в (5), а затем результат в (4), получим
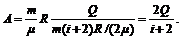 (7)
(7)
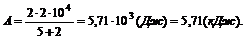
Вывод размерности: из формулы (7) имеем
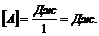
Ответ: А = 5,71∙103 Дж.
13). Задача на применение I закона термодинамики.
Воздух массой 100г, температура которого 270С, нагревается при постоянном давлении и его объем увеличивается в 2 раза. Найти количество теплоты, которое пошло на нагревание воздуха, работу газа при расширении, приращение внутренней энергии.
Запишем краткое условие задачи.
Решение: Количество теплоты сообщенное воздуху: |
Дано: СИ
m=100г =0,1кг
t1=270C T1=300К
V2=2V1

 Q, A, ΔU-?
Q, A, ΔU-?
где сp=103Дж/(кг·К)- удельная теплоемкость воздуха при постоянном давлении (из справочной таблицы). По закону Гей – Люссака ![]() , отсюда
, отсюда 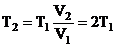 . Работа газа при изобарическом процессе равна:
. Работа газа при изобарическом процессе равна: 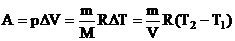 . Приращение внутренней энергии по I закону термодинамики:
. Приращение внутренней энергии по I закону термодинамики: 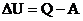 .
.
Проведем проверку размерности:
![]() .
.
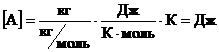 .
.
![]()
Молярная масса воздуха: M=29·10-3кг/моль.
Произведем вычисления:
![]() ,
, 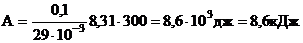 ,
, ![]()
Ответ: 30 кДж, 8,6кДж, 21,4кДж.
14). Задача на КПД тепловой машины.
Температура нагревателя и холодильника идеальной тепловой машины соответственно равны 1170С и 270С. Количество теплоты, получаемое от нагревателя за 1 с, равно 60 кДж. Найдите КПД машины, количество теплоты, отдаваемое холодильнику в 1с, и мощность машины.
Запишем краткое условие задачи
Решение: КПД тепловой машины: |
Дано: СИ
 t1=1170С T1=390K
t1=1170С T1=390K
t2=270С T2=300K
Q1=60кДж =60·103Дж
t=1c
 Q2? N-?
Q2? N-?
машины 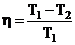 . Приравниваем правые части:
. Приравниваем правые части: ![]()
![]()
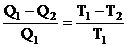
![]()
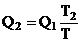 .
.
Мощность тепловой машины 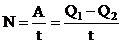 .
.
Произведем вычисления: ![]() ,
, 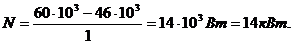
Ответ: 46 кДж, 14 кВт.
6. Задачи для контрольной работы
Контрольная работа №1
Варианты. | Номера задач |
1 2 3 4 5 6 7 8 9 0 | 31 171 32 172 33 173 34 174 35 175 36 176 37 177 38 178 39 179 140 180 |
1-1. Прямолинейное движение точки описывается уравнением 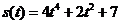 м. Найти скорость и ускорение точки в момент времени 2с, а также среднюю скорость и среднее ускорение за первые две секунды движения и за вторые две секунды движения.
м. Найти скорость и ускорение точки в момент времени 2с, а также среднюю скорость и среднее ускорение за первые две секунды движения и за вторые две секунды движения.
1-2. Кинематические уравнения двух материальных точек имеют вид ![]() и
и 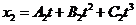 , где
, где ![]() ,
, 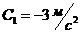 ,
, ![]() ,
, 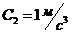 . Определить момент времени, для которого ускорения этих точек будут равны.
. Определить момент времени, для которого ускорения этих точек будут равны.
1-3. Зависимость пройденного телом пути от времени задаётся уравнением ![]() , где
, где 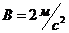 ,
, ![]() ,
, 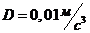 . В какой момент времени ускорение тела будет равно
. В какой момент времени ускорение тела будет равно ![]() , и чему равно среднее ускорение тела за этот промежуток времени?
, и чему равно среднее ускорение тела за этот промежуток времени?
1-4. Движение двух материальных точек выражается уравнениями ![]() и
и 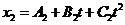 , где
, где ![]() ;
; ![]() ;
; 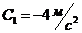 ;
; ![]() ;
; 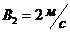 ;
;![]() . В какой момент времени скорости этих точек будут одинаковы? Чему равны скорости и ускорения этих точек?
. В какой момент времени скорости этих точек будут одинаковы? Чему равны скорости и ускорения этих точек?
1-5. Нормальное ускорение точки, движущейся по окружности радиусом 4 м, задаётся уравнением ![]() (
(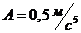 ). Определить: 1) тангенциальное ускорение точки в момент времени 5c; 2) путь, пройденный точкой за время 5 с после начала движения; 3) полное ускорение для момента времени 1 с.
). Определить: 1) тангенциальное ускорение точки в момент времени 5c; 2) путь, пройденный точкой за время 5 с после начала движения; 3) полное ускорение для момента времени 1 с.
1-6. Уравнение движения материальной точки вдоль оси имеет вид ![]() , где
, где ![]() м,
м, 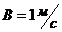 ,
, ![]() . Найти координату
. Найти координату ![]() , скорость и ускорение точки в момент времени 2с.
, скорость и ускорение точки в момент времени 2с.
1-7. Две материальные точки движутся согласно уравнениям 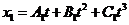 и
и ![]() , где
, где 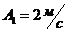 ;
;![]() ;
; 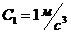 ;
; ![]() ;
; 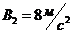 ;
; ![]() . В какой момент времени скорости этих точек будут одинаковы? Найти ускорения точек в этот момент времени.
. В какой момент времени скорости этих точек будут одинаковы? Найти ускорения точек в этот момент времени.
1-8. Материальная точка движется прямолинейно. Уравнение движения имеет вид ![]() , где
, где 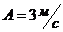 ,
, ![]() .Найти скорость и ускорение точки в момент времени
.Найти скорость и ускорение точки в момент времени ![]() и
и ![]() с.
с.
1-9. Зависимость пройденного телом пути от времени дается уравнением ![]() , где
, где ![]() м,
м, ![]() и
и 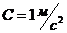 . Найти среднюю скорость и среднее ускорение за первую, вторую и третью секунды его движения.
. Найти среднюю скорость и среднее ускорение за первую, вторую и третью секунды его движения.
1-10.Кинематические уравнения движения двух материальных точек имеют вид ![]() и
и 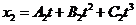 , где
, где ![]() ,
,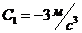
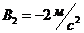
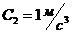 . Определить момент времени, для которого ускорения этих точек будут равны.
. Определить момент времени, для которого ускорения этих точек будут равны.
1-11.Колесо вращается с постоянным угловым ускорением ![]() . Определить радиус колеса, если через 2 с после начала движения полное ускорение колеса
. Определить радиус колеса, если через 2 с после начала движения полное ускорение колеса ![]() .
.
1-12.Колесо автомашины вращается равнозамедленно. За время 2 мин оно изменило частоту вращения от 240 до 60 ![]() . Определить 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
. Определить 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
1-13.Маховик, бывший неподвижным, начал вращаться равноускоренно и приобрёл угловую скорость 12 об/c, сделав 40 полных оборотов. Определить угловое ускорение маховика и продолжительность равноускоренного вращения.
1-14.Точка движется по окружности радиусом ![]() см с постоянным тангенциальным ускорением. Найти это ускорение, если к концу пятого оборота после начала движения скорость точки стала 79,2 м/с.
см с постоянным тангенциальным ускорением. Найти это ускорение, если к концу пятого оборота после начала движения скорость точки стала 79,2 м/с.
1-15.Колесо, вращаясь равнозамедленно, при торможении уменьшило свою скорость с 300 об/мин до 180 об/мин. За это время оно сделало 240 полных оборотов. Найти угловое ускорение колеса и время торможения.
1-16.Колесо радиусом R=0,1 м, вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением ![]() Для точек, лежащих на ободе колеса, найти через 2 с после начала движения следующие величины: 1) угловую скорость, 2) угловое ускорение, 3) нормальное ускорение.
Для точек, лежащих на ободе колеса, найти через 2 с после начала движения следующие величины: 1) угловую скорость, 2) угловое ускорение, 3) нормальное ускорение.
1-17.На цилиндр, вращающийся около горизонтальной оси, намотана нить. К концу нити привязали груз и предоставили ему возможность опускаться. Двигаясь равноускоренно, груз за 5 с опустился на 1,5 м. Определить угловое ускорение цилиндра и его угловую скорость, если радиус цилиндра равен 4 см.
1-18.Вал делает 180 об/мин. С некоторого момента вал тормозится и вращается равнозамедленно с угловым ускорением, равным 3 рад/с2. Через сколько времени вал остановится? Сколько оборотов сделает вал до остановки?
1-19.Колесо, вращаясь с частотой 1500 об/мин, при торможении стало вращаться равнозамедленно и остановилось через 30 с. Найти угловое ускорение и число оборотов с момента начала торможения до остановки.
1-20.Маховик, приведенный в равноускоренно движение, сделав 40 полных оборотов, приобрел угловую скорость, соответствующую 480 об/мин. Определить угловое ускорение маховика и продолжительность равноускоренного движения.
1-21. Шар, массой 200г движется перпендикулярно стене со скоростью 5 м/с и отскакивает от нее со скоростью 3 м/с. Определить силу взаимодействия шара со стеной, если время взаимодействия 0.1с.
1-22.Студент массой 80 кг стоит на весах в лифте. Что покажут весы, если лифт поднимается с ускорением 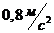 ? Движется равномерно со скоростью
? Движется равномерно со скоростью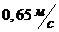 ? Опускается с ускорением
? Опускается с ускорением 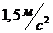 ?
?
1-23.Поезд массой 1000 тонн, двигаясь в течение времени 10 мин уменьшает свою скорость от 48 км/ч до 18 км/ч. Найти силу торможения, полагая, что ускорение поезда постоянно.
1-24.Тело массой 10 кг движется прямолинейно. Зависимость пройденного телом пути S от времени t дается уравнением ![]() , где
, где 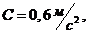
![]()
![]() . Найти силу, действующую на тело в момент времени 0,2 с.
. Найти силу, действующую на тело в момент времени 0,2 с.
1-25.Грузы массами 0,5 кг и 0,3 кг соединены нитью и перекинуты через невесомый блок, укреплённый на конце стола. Коэффициент трения груза ![]() о стол 0,15. Пренебрегая трением в блоке, определить: 1) ускорение, с которым движутся грузы; 2) силу натяжения нити.
о стол 0,15. Пренебрегая трением в блоке, определить: 1) ускорение, с которым движутся грузы; 2) силу натяжения нити.
1-26.Мотоциклист едет по горизонтальной дороге со скоростью 72 км/ч, делая поворот радиусом кривизны в 100 м. Под каким углом к горизонту он должен наклониться, чтобы не упасть при повороте?
1-27.Тело массой 3 кг падает в воздухе с ускорением 8 м/с2. Найти силу сопротивления воздуха.
1-28.К саням массой 350 кг приложена сила 500 Н под углом ![]() к горизонтальной поверхности. Определить коэффициент трения саней о лед, если сани движутся с ускорением 0,8 м/с2.
к горизонтальной поверхности. Определить коэффициент трения саней о лед, если сани движутся с ускорением 0,8 м/с2.
1-29.Тело массой 2 кг движется прямолинейно по закону ![]() ;
;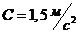 ,
,![]() Определить силу, действующую на тело в конце второй секунды движения.
Определить силу, действующую на тело в конце второй секунды движения.
1-30.К концам шнура, перекинутого через неподвижный блок, подвешены грузы в 19,6 Н и 29,4 Н. С каким ускорением движутся грузы и какова сила натяжения шнура? Массой блока пренебречь.
1-31.Определить силу, которую необходимо приложить к ободу блока вращающегося с частотой 12с-1, чтобы он остановился в течение 8с. Диаметр блока 30 см. Массу блока в 6 кг считать равномерно распределенной по всему блоку.
1-32.Шар в одном случае соскальзывает без вращения, в другом скатывается с наклонной плоскости с высоты 2 м. Определить скорости в конце спуска в двух случаях. Трением пренебречь.
1-33.Маховик вращался, делая 2 об/с. Под действием тормозящего момента 100 Н·м он остановится через 2 мин. Определить момент инерции маховика.
1-34. Тонкостенный цилиндр с диаметром основания 30 см и массой 12 кг вращается согласно уравнению 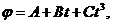 где
где 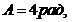
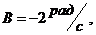
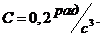 Определить действующий на цилиндр момент сил в момент времени 3с.
Определить действующий на цилиндр момент сил в момент времени 3с.
1-35. На обод маховика диаметром 60см намотан шнур, к концу которого привязан груз массой 2кг. Определить массу маховика, если он, вращаясь равноускоренно, под действием силы тяжести груза, за время 3с приобрел угловую скорость 9 рад/с. Считать массу маховика равномерно распределенной по всему его объему.
1-36. Диск массой 0,5 кг и диаметром в 40 см вращается, делая 1500 об/мин. При торможении он останавливается в течение 20с. Определить тормозящий момент.
1-37. Какую силу нужно приложить к валу махового колеса, чтобы в течение одной минуты довести скорость вращения до 2 об/с? Радиус вала 20 см; массу маховика в 500 кг считать распределенной по ободу на расстоянии 1 м от оси вращения.
1-38.Найти момент инерции и момент импульса однородного шара, который вращается вокруг своей оси, делая 10 об/с. Масса шара равна 2 кг, радиус составляет 50 см.
1-39.Стержень длиной 60 см и массой 0,4 кг вращается с угловым ускорением 10с-2 вокруг перпендикулярной оси, проходящей через его середину. Найти вращающий момент.
1-40.Маховик, имеющий вид диска, массой 100кг и радиусом 0.5м вращался, делая 360 об/мин. На его цилиндрическую поверхность начала действовать тормозящая сила, равная 20Н. Сколько оборотов сделает диск до остановки.
1-41.На железнодорожной платформе, движущейся по инерции со скоростью 3 км/ч, укреплено орудие. Масса платформы с орудием 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой 10 кг вылетает из ствола под углом 60о к горизонту. Определить скорость снаряда (относительно земли), если после выстрела скорость платформы уменьшилась в 2 раза.
1-42.Определить к. п.д. неупругого удара бойка массой 0,5т, падающего на сваю массой 120 кг. Полезной считать энергию, пошедшую на вбивание сваи.
1-43.Тело массой 0.5 кг падает с высоты 2 м на плиту массой 1 кг, закрепленную на пружине с жесткостью 4 кН/м. Определить, на какую длину сожмется пружина, если удар является абсолютно неупругим.
1-44.На железнодорожной платформе установлено орудие. Масса платформы с орудием 15 тонн. Орудие стреляет вверх под углом 60о к горизонту в направлении пути. С какой скоростью покатиться платформа вследствие отдачи, если масса снаряда 20 кг и он вылетает со скоростью 600 м/с.
1-45.Автомашина массой 1.8 т движется в гору, уклон которой составляет 3м на каждые 100 м пути. Определить 1)работу, совершаемую двигателем автомашины на пути 5 км, если коэффициент трения 0.1; 2) развиваемую двигателем мощность, если известно, что этот путь был преодолен за время 5 мин.
1-46. Шар массой 10кг сталкивается с шаром массой 4 кг. Скорость первого шара 4 м/с, второго 12 м/с. Найти общую скорость шаров после удара в двух случаях: 1)когда малый шар нагоняет большой шар, движущийся в том же направлении; 2) когда шары движутся навстречу друг другу. Удар считать прямым, центральным, неупругим.
1-47.Пуля массой 12 г, летящая с горизонтальной скоростью 0,6 км/с, попадает в мешок с песком массой 10 кг, висящий на длинной нити, и застревает в нем. Определить, 1) высоту, на которую поднимется мешок, отклонившись после удара; 2) долю кинетической энергии, израсходованной на пробивание песка.
1-48.Тело брошено вертикально вверх со скоростью 20 м/с. Пренебрегая сопротивлением воздуха, определить, на какой высоте кинетическая энергия тела будет равна его потенциальной энергии.
1-49.Определить потенциальную энергию растянутой на 10 см пружины, если известно, что под действием силы 30 Н пружина растягивается на 2 см.
1-50. Поезд массой 600 т отходит от станции и через 5 минут после отхода имеет скорость 60 км/ч, пройдя путь 2 ,5 км. Какую среднюю мощность развивал паровоз, если коэффициент трения постоянен и равен 0,05?
1-51.Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением 0,4 рад/с2. Определить кинетическую энергию маховика через 25 с после начала движения, если через 10 с после начала движения момент импульса маховика составлял 60 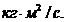
1-52.Человек массой 60 кг, стоящий на краю горизонтальной платформы радиусом 1 м и массой 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой 10 мин-1, переходит к ее центру. Считая платформу круглым однородным диском, а человека – точечной массой, определить работу, совершаемую человеком при переходе от края платформы к ее центру.
1-53.Кинетическая энергия вала, вращающегося с постоянной скоростью, соответствующей 5 об/с, равно 60 Дж. Найти момент импульса этого вала.
1-54.На маховик с моментом инерции 0,5 кг·м2 действовал в течение 10с вращающий момент, равный 4 Н·м. Определить кинетическую энергию, приобретенную маховиком.
1-55.К ободу диска массой 5 кг приложена постоянная касательная сила 19,6 Н. Какую кинетическую энергию будет иметь диск через 5 с после начала действия силы?
1-56.Маховик в виде диска начинает вращаться с угловым ускорением 0,5 с-2 и через 20 с его кинетическая энергия становится равной 500 Дж. Какой момент импульса приобретает он через 15 мин после начала движения?
1-57.Снаряд массой 400 кг движется со скоростью 780 м/с, делая 5270 об/мин. Определить, во сколько раз энергия поступательно движения больше энергии его вращательного движения. Момент инерции снаряда 4,9 кг·м2.
1-58. Шар катится без скольжения по горизонтальной поверхности. Полная кинетическая энергия шара 14 Дж. Определить кинетическую энергию поступательного и вращательного движения шара.
1-59.Снаряд, имеющий вид цилиндра диаметром 0,06 м летит со скоростью 400 м/с и вращается, совершая 500 об/с. Найти его полную кинетическую энергию. Масса равна 15 кг.
1-60.Диск, катившийся без скольжения со скоростью 3 м/с, ударился о стенку и покатился со скоростью 2 м/с. Масса диска 3 кг. Определить уменьшение кинетической энергии диска.
1-61. Уравнение движения точки в виде![]() . Найти максимальную скорость, максимальное ускорение, а также моменты времени, в которые достигаются эти максимальные значения.
. Найти максимальную скорость, максимальное ускорение, а также моменты времени, в которые достигаются эти максимальные значения.
1-62.Написать уравнение гармонического колебательного движения с амплитудой 5 см, если за время 1 мин совершается 150 колебаний и начальная фаза колебаний ![]() .
.
1-63. Определить смещение, скорость и ускорение гармонически колеблющейся точки через 1/40с после начала колебания, если амплитуда 1см и частота 10с-1.Начальная фаза равна 0.
1-64.Уравнение колебаний материальной точки имеет вид ![]() см. Определить ускорение точки в тот момент, когда ее смещение равно 0.5 см.
см. Определить ускорение точки в тот момент, когда ее смещение равно 0.5 см.
1-65.Определить максимальное ускорение материальной точки, совершающей гармонические колебание с амплитудой 15 см, если наибольшая скорость точки равна 30 см/с. Напишите также уравнение колебаний.
1-66.Период гармонических колебаний точки равен 2,4 с, амплитуда 5 см, начальная фаза равна нулю. Каковы смещение, скорость и ускорение точки через 0,4 с после начала колебаний?
1-67.Начальная фаза колебаний точки 15 градусов. Через сколько времени от начала движения смещение точки первый раз достигнет величины, равной половине амплитуды. Период колебаний равен 12с.
1-68.Написать уравнение колебательного движения материальной точки, совершающей колебания с амплитудой 5 см, периодом 1 с и начальной фазой 45 градусов.
1-69.Уравнение колебаний дано в виде ![]() см. Найти период колебания, максимальную скорость и максимальное ускорение.
см. Найти период колебания, максимальную скорость и максимальное ускорение.
1-70.Через сколько времени от начала движения точка, совершая гармонические колебания с периодом 12 с и начальной фазой, равной нулю, сместится от положения равновесия на расстояние, равное половине амплитуды?
1-71.Написать уравнение гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями ![]() и
и ![]() .
.
1-72. Уравнение движения материальной точки массой 5 грамм имеет вид 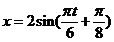 см. Определить максимальную возвращающую силу и полную энергию колебаний.
см. Определить максимальную возвращающую силу и полную энергию колебаний.
1-73.Найти максимальную кинетическую энергию материальной точки массой 2 г, совершающей гармонические колебания с амплитудой 4 см и частотой 5 Гц.
1-74. Уравнение колебаний материальной точки массой 0,2 г, имеет вид ![]() (длина в см, время в с). Определить период колебаний, максимальное значение кинетической энергии и максимальную величину возвращающей силы.
(длина в см, время в с). Определить период колебаний, максимальное значение кинетической энергии и максимальную величину возвращающей силы.
1-75. Две точки находятся на прямой, вдоль которой распространяются волны со скоростью 10 м/с. Период колебаний 0,2с, расстояние между точками 1 м. Найти разность фаз колебаний в этих точках.
1-76. Точка совершает гармонические колебания, уравнение которых имеет вид 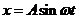 , где А= 5см, ω=2с-1. Найти момент времени(ближайший к началу отсчёта), в который потенциальная энергия точки 10-4 Дж, а возвращающая сила
, где А= 5см, ω=2с-1. Найти момент времени(ближайший к началу отсчёта), в который потенциальная энергия точки 10-4 Дж, а возвращающая сила ![]() Н. Определить также фазу колебаний в этот момент времени.
Н. Определить также фазу колебаний в этот момент времени.
1-77.Две точки лежат на луче и находятся от источника колебаний на расстояниях x1=4 м и х2=7 м. Период колебаний Т=20мс и скорость распространения волны 300 м/с. Определить разность фаз колебаний в этих точках.
1-78.Разность фаз двух одинаково направленных гармонических колебаний одинакового периода 4 с и одинаковой амплитуды 5 см составляет ![]() . Написать уравнение движения, получающегося в результате сложения этих колебаний, если начальная фаза одного из них равна нулю.
. Написать уравнение движения, получающегося в результате сложения этих колебаний, если начальная фаза одного из них равна нулю.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 |




