Сумма и пересечение подпространств. Прямая сумма подпространств.

Пусть L – линейное пространство над полем Р, А и В – его подпространства. Суммой подпространств А и В называют множество А+В={a+b | аА, b B}.

Пример 1. На плоскости векторы, лежащие на оси ОХ, составляют подпространство А; векторы, лежащие на оси ОY, составляют подпространство В. Множество А+В совпадает с , в чем можно убедиться, проверив включения А+В и А+В.

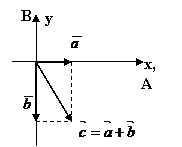
Теорема. Сумма подпространств А и В линейного пространства L является его подпространством.

Утверждения:

1.  Базис суммы подпространств А=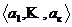, В=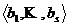 совпадает с базисом системы векторов .

2.  Размерность А+В равна рангу системы векторов .

Пример 2. В линейном пространстве A4 даны подпространства А= и В=, где =(1, 2, ‑1, 3), =(2, 1, 4, 2), =(4, 5, 2, 8), =(6, 6, 6, 8), =(5, 4, 7, 7), =(4, 2, 8, 6). Найти базис и размерность подпространства А+В.

Решение. Найдем базис А и базис В. Составляем матрицы М и N и ищем их ранги. Матрица М составлена из координат векторов по строкам. Матрица N составлена из координат векторов по строкам.

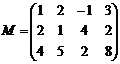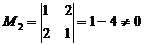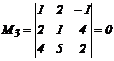
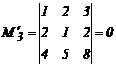, , , значит r(M)=2, поэтому dim(A)=2.

Векторы , составляют базис А, т. к. координаты этих векторов проходят через базисный минор М2.

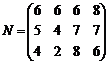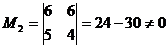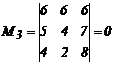
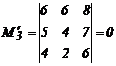, , , значит r(N)=2, поэтому dim(B)=2.

Векторы , составляют базис В, т. к. координаты этих векторов проходят через базисный минор М2.

Тогда А+В=<a1, a2, b1, b2>. Найдем базис системы векторов {a1, a2, b1, b2}. Для этого надо найти ранг матрицы Н, строки которых – координаты данных четырёх векторов.

, ,

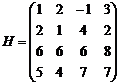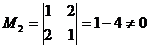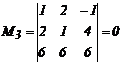
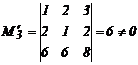
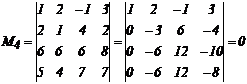
Значит r(H)=3. Так как в базисный минор входят координаты векторов , , b1 то базис А+В составляют векторы , , , dim(А+В)=3.

Пересечением подпространств А и В линейного пространства L называется множество .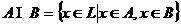

Теорема. Пересечение подпространств линейного пространства L является подпространством L.

Теорема. Размерность суммы подпространств равна сумме размерностей слагаемых без размерности их пересечения, т. е.

dim(A+B)=dim(A)+dim(B)–dim(A B) (1)

Из этой формулы находим размерность AB:

dim(A B)=dim(A)+dim(B)–dim(A+B).

Так как размерности подпространств в правой части этого равенства мы умеем находить, то по этой формуле можно найти dim(A B).

Пример 3. Для подпространств А и В из примера 2 найти базис и размерность подпространства A B.

Решение. Мы нашли, что dim(А+В)=3, dim(A)=2, dim(B)=2. Подставляя в формулу (1),имеем:

3=2+2–dim(A B).

Таким образом, dim(A B)=1. Теперь остается найти базис A B. Для этого достаточно найти один ненулевой вектор из A B, он и составит базис A B.

Пусть х A B, тогда x=t1a1+t2a2=t1(1, 2, ‑1, 3)+t2(2, 1, 4, 2) и x=s1b1+s2b2=s1(6, 6, 6, 8)+s2(5, 4, 7, 7),

t1(1, 2, ‑1, 3)+t2(2, 1, 4, 2)=s1(6, 6, 6, 8)+s2(5, 4, 7, 7),

откуда получим

Записываем покомпонентно это равенство, получаем систему линейных однородных уравнений относительно неизвестных .

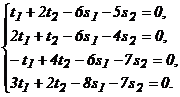
Решаем систему методом Гаусса:

, , .

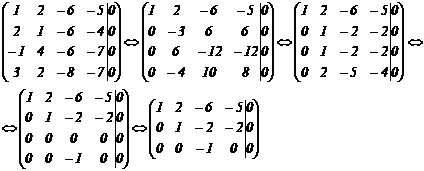
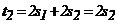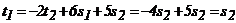Найдём ненулевое частное решение этой системы, придав свободной неизвестной s2 ненулевое значение, например s2=1.

При выбранном значении s2 переменные t1=1 и t2=2. Записываем вектор х:

x=t1a1+t2a2=1∙(1, 2, ‑1, 3)+2∙(2, 1, 4, 2)=s1b1+s2b2=(5, 4, 7, 7).

Мы нашли ненулевой вектор из пересечения AB, он составляет базис A B. Подпространство A B =.

Если подпространства А и В заданы однородными системами уравнений, то пересечение A B будет определяться системой, полученной объединением всех уравнений из этих систем. Любая фундаментальная система решений такой системы уравнений является базисом пересечения AB.

Пример 4. Пусть подпространства А и В заданы соответственно системами уравнений

()

()

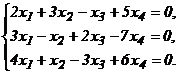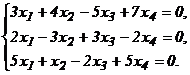Найти базис и размерность подпространств А+В и A B.

Решение. Исследуем систему ()

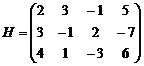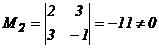, , r(H)≥2

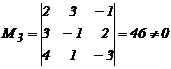, значит r(H)=3.

Исследуем систему ()

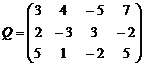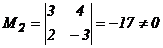, , r(Q)≥2

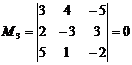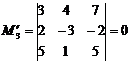, , значит r(Q)=2.

Подпространство В задается системой

()

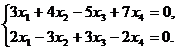Для нахождения А+В определяем базис А (ФСР системы уравнений ()) и базис В (ФСР системы уравнений ()). Решаем систему (). ФСР состоит из одного решения (n‑r=4‑3=1), – основные неизвестные, – свободное неизвестное. Получаем систему из системы ():

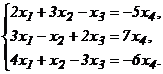
Решим систему методом Гаусса:

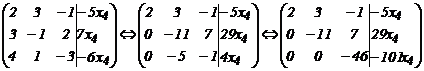
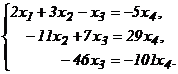
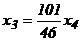
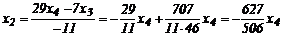
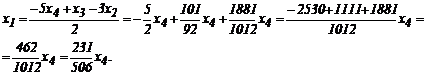ФСР: 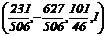или (231, ‑627, 1111, 506). Базис пространства А – это вектор (231, ‑627, 1111, 506)=а.

Решаем систему (). ФСР состоит из двух решений (n‑r=4‑2=2). Основные неизвестные – , свободные – .

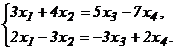
1

0

0

1

1).  ,

=, =.

2).  ,

=, =.

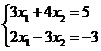
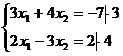
В качестве базиса подпространства В можно взять векторы

и . Тогда

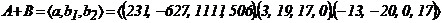Посмотрим, является ли система векторов линейно зависимой или линейно независимой.

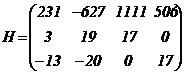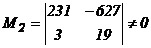, , r(H)≥2

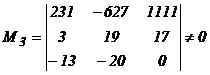r(H)=3. Система векторов линейно независима, является базисом (А+В).

Найдем размерность пересечения (AB) подпространств.

3=2+1–dim(A B), dim(AB)=0, AB=0. Базиса нет. Для нахождения базиса пересечения подпространств AB следует решить систему уравнений

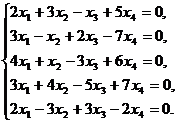
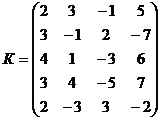
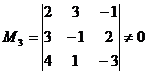
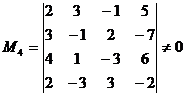
r(K)=4 r=n система имеет единственное нулевое решение. Поэтому A B=0. Базиса подпространства АВ нет.

Пусть в L имеем подпространства А и В. Может оказаться, что АВ=0. Тогда сумма подпространств А+В называется прямой суммой и обозначается А+В=АВ.

Подпространство А+В обозначим через Н: Н=А+В, Н. Тогда записывают: Н=АВ, если Н=L,то L=АВ, и говорят: подпространство Н (линейное пространство L) является прямой суммой подпространств А и В. Если L=АВ, то подпространства А и В называют прямыми дополнениями друг друга в пространстве L.

Теорема. Сумма подпространств А и В тогда и только тогда является прямой, когда размерность суммы подпространств А и В равна сумме размерностей слагаемых, т. е.:

dim(A+B)=dim(A)+dim(B).

Пример 6. Подпространства А и В из примера 4 составляют прямую сумму, так как A B=0.