ПРАКТИЧЕСКИЕ РАБОТЫ НА 9 СЕМЕСТР ПО КУРСУ «СИСТЕМЫ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА»
Каждая работа содержит несколько вариантов поставленных задач. Сложность отдельных задач в каждом из заданий в среднем одинаковая, с небольшими отклонениями. Для выполнения работы необходимо выбрать для реализации одно из входящих в его состав заданий. Выбирайте то задание, которое вам наиболее понятно, потому что решить задачу, которую вы совершенно не понимаете (отвлекаясь от программирования) в общем случае невозможно. При непонимании всех заданий из работы не делайте ничего на авось, а обратитесь к преподавателю и, возможно, вам будет предложено индивидуальное задание другой сложности на аналогичную тему.
Творческий подход при выполнении работ приветствуется, однако элементы творчества не должны никоим образом отражаться на поставленной задаче и модифицировать её в сторону уменьшения сложности или сокращения функциональности без специального разрешения.
Работы могут выполняться на любом языке программирования по желанию студента, лишь бы был правильный результат. При возникновении каких-либо технических сложностей при выполнении той или иной работы, следует обратиться к преподавателю, что наверняка приведёт к формулировке некоторой упрощённой версии задания, вызвавшего затруднения, что, однако, не изменит его сути.
Работа №1
Задание: Построение графа
Работа является вводной. Её главная цель – освежить в памяти навыки построения деревьев и графов и работы с ними, поскольку две следующие работы в той или иной степени потребуют этих навыков в увеличенном объёме. Общие принципы построения и вывода на экран графов изучались вами в третьем семестре в курсе «Структуры и алгоритмы обработки данных на ЭВМ» и должны быть вам знакомы. С тех пор принципиально ничего не изменилось.
В рамках работы требуется написать программу, позволяющую отобразить на экране граф, информация о котором указана в определённом (на усмотрение студента) формате в обычном текстовом файле.
Для определённости и возможности отображения того, что будет указано в файле, ограничим число уровней графа четырьмя (4), а максимальную ширину одного уровня графа семью (7) вершинами. Граф таких размеров можно легко уместить на экране любого монитора. Граф будет иметь одну вершину, которую мы условно назовём корневой и договоримся, что при отображении корневой будет та вершина, которая указанна в файле первой.
В каком виде указывать вершины графа и какими дополнительными данными сопровождать каждую из вершин – дело ваше, главное, чтобы на основании указаний в файле программа смогла построить именно тот граф, который мы ожидаем.
Чтобы прояснить ситуацию, приведём пример.
Допустим, мы хотим, чтобы программа построила и отобразила следующий граф:
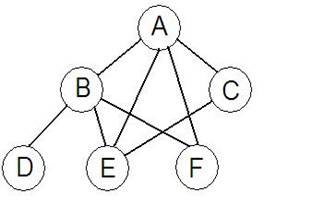
Для того чтобы задать этот (или любой подобный) граф, необходимо знать о нём следующее:
- какой узел является корневым;
- на скольких уровнях расположены вершины графа;
- какова ширина самого широкого уровня;
- какое максимальное число потомков могут иметь узлы графа;
- список потомков для каждого узла.
Владея подобной информацией для любого графа, можно написать программу, которая построит его и отобразит на экране.
Чтобы не указывать в текстовом файле все перечисленные сведений о выводимом графе, из списка нужно выбрать только те, которые действительно необходимы, а именно: список вершин графа и их потомков. Корневой узел, как было сказано, заносится в файл первым, поэтому специально обозначать его не следует. Имея список вершин графа и потомков каждой вершины, всегда можно посчитать число уровней графа, максимальную ширину уровня и максимальное число потомков некоторой вершины. Таким образом, для отображения любого графа необходимо иметь лишь список вершин и потомков каждой вершины. Список потомков можно разделять, например, запятыми, а имя вершины от списка потомков можно отделять, например, двоеточием. Приведём пример такого текстового файла, в котором содержится информация о нарисованном графе:
A: B, E, F, C
B: D, E, F
C: E
D:
E:
F:
Имея файл с подобным содержимым, легко построить граф и вывести его узлы на экран. Каждый узел графа в программе следует представить либо структурой, либо объектом, либо каким-то другим способом, который вы придумаете, если придумаете. Обратите внимание, что на основании представленного файла легко узнать максимальное допустимое число потомков некоторого узла графа (В данном случае это будет 4 – число потомков узла А).
Узнав максимально возможное число потомков узла, в языке, например, СИ, можно объявить для его хранения примерно такую структуру:
struct node {
char: name;
struct node *children[4];
struct node *parent;
};
Поле name будет хранить букву, соответствующую вершине (в следующих работах вместо буквы потребуется хранение состояния игрового поля), в массиве children будут храниться указатели на потомков текущего узла, а поле parent будет содержать указатель на родительский узел (в данной работе он не нужен, а в следующий будет очень полезен).
Всё, структура есть, осталось только на основании данных в текстовом файле сформировать требуемое дерево и вывести его каким-либо образом на экран.
Вывод на экран может быть реализован аналогично тому, как это делалось в лабораторных работах на втором курсе (каждая вершина содержала координаты, в которые её необходимо вывести), либо более интеллектуальным способом. Каким – решать вам. Обратите внимание, что каждую из вершин следует отображать на уровень ниже последнего встречающегося в файле родителя вершины. Например, хотя узел Е является потомком узла А, его следует отображать не на следующем за А уровнем, а через уровень, потому что помимо вершины А родителем узла Е являются узлы В и С, которые как раз и располагаются на уровень ниже А.
Время на выполнение работы – 2 занятия.
Работа №2
Задание: решение головоломки «Восьмёрки» с использованием поиска в пространстве состояний
Всем, конечно же, известна такая древняя интеллектуальная игра, как «Пятнашки». «Восьмёрки» - это аналог пятнашек, выполненный на поле размером не 4х4, а на поле размером 3х3. В рамках данной работы предлагается реализовать возможность решения «восьмёрок» с помощью простейшего и не слишком интеллектуального подхода – с помощью поиска решения в дереве пространства состояний.
Выполнение работы можно условно поделить на 3 этапа:
1. Построение полного дерева пространства состояний для «восьмёрок».
2. Нахождение текущей комбинации игрового поля в пространстве состояний с помощью поиска «в ширину» или поиска «в глубину».
3. Получение на основании имеющегося дерева таких комбинаций игрового поля, последовательный переход по которым приведёт к решению поставленной задачи – сбору головоломки.
Рассмотрим каждый из этапов немного подробнее.
Построение дерева выполнялось вами в первой лабораторной работе и в случае, если всё было сделано правильно – весь наработанный код можно легко использовать при реализации данной работы. Дерево пространства состояний для восьмёрок должно строиться из целевой комбинации, которой является следующая:
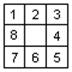
В отличие от предыдущей работы, в данной конкретной задаче число потомков каждого узла будет максимум 4, как, например, при построении их из исходной комбинации. Каждый потомок некоторой вершины будет содержать возможные состояния игрового поля, в которые можно попасть, сделав ход из текущей вершины. Перед добавлением некоторого потомка в дерево пространства состояний необходимо убедиться, что там его ещё нет. В противном случае, дерево рискует получиться бесконечно большим. Из целевой комбинации можно сделать 4 различных хода: сдвинуть «8» вправо, «4» влево, «2» вниз или «6» вверх. Отобразив это в виде дерева, получим следующую картину:
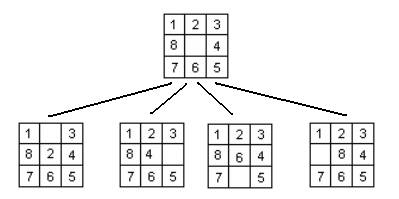 |
Каждая из листовых вершин представленного дерева содержит состояние игрового поля, из которого можно сделать 3 различных хода, один из которых уже есть в представленном дереве: это корень дерева. По этой причине, каждый из представленных листовых узлов будет иметь не 3, а только 2 потомка. Продолжая построение дерева подобным образом, можно в итоге прийти к ситуации, когда ни из одной листовой вершины нет возможности сделать ход, который ещё не делали. При достижении подобной ситуации следует прийти к выводу, что дерево решений (пространство состояний игры «восьмёрки») построено, и его можно использовать.
При наличии построенного дерева, можно переходить к реализации интерфейса игры. Пользователь должен иметь возможность видеть игровое поле в каждый момент времени, должен иметь возможность перемещать фишки игрового поля допустимым образом, а также должен иметь возможность, нажав некоторую кнопку, запустить процесс автоматического сбора головоломки. В момент запуска автоматического сбора следует запустить нахождение текущей комбинации игрового поля в пространстве состояний с помощью поиска «в ширину» или поиска «в глубину». Какой из видов поиска выбирать – дело ваше. Главное, чтобы искомая комбинация присутствовала в построенном дереве решений. Независимо от выбранного вида поиска, пройденный по дереву путь следует сохранять.
Наличие сохранённых комбинаций, по которым выполнялся поиск, позволит получить путь от текущего состояния игрового поля к целевому. О том, как это сделать – было сказано на лекциях. После получения пути решения, его следует отобразить в виде последовательности деланных ходов для сбора головоломки, после чего задачу можно считать решённой.
В процессе выполнения работы возможно появление следующих проблем:
1. Построение дерева пространства состояний вызывает нехватку памяти. Если это произошло – введите в программу возможность строить не полное дерево, а дерево до какого-то конкретного уровня. Практика показывается, что, построив дерево хотя бы до уровня 8 или 9, вы легко сможете отладить весь остальной код.
2. Всё сделано правильно, но иногда программа зависает, уходя в бесконечный цикл. Обычно это происходит из-за того, что первоначальная комбинация игрового поля формируется случайно расстановкой фишек в случайные позиции. Подобный подход быстр, но в половине случаев приводит к зацикливанию алгоритма, поскольку половина комбинаций из всех возможных случайных расстановок фишек сбору по правилам поддаваться не будет. Избежать этого можно очевидным способом - в начале работы программы для получения комбинации, требующей сборки, необходимо размешивать собранную комбинацию.
3. Дерево построено, комбинация игрового поля найдена, а как получить путь к вершине дерева на основе имеющегося списка пройденных состояний – не совсем понятно. Решить эту проблему можно введением в каждый узел дерева указателя на родительский узел. Тогда, зная в каком из узлов вы в данный момент находитесь, можно всегда путём перехода по ссылками на родительские узлы подняться к вершине.
Задание: реализация интеллектуального противника в игре «крестики-нолики» с использованием поиска в пространстве состояний
Задание аналогично предыдущему, с разницей лишь в том, что программа предназначена не просто для сбора головоломки, а для игры с человеком, который по своей природе враждебен. Для того чтобы компьютер мог ходить и наносить урон противнику , его действия должны быть на чём-то основаны. В данной работе основанием предлагается сделать дерево решений игры «крестики-нолики». Для простоты можно условиться, что первым всегда ходит человек. Таким образом, дерево решений программы следует начинать строить с того состояния игрового поля, в котором оно окажется после первого хода человека.
После построения дерева, компьютеру следует найти в этом дереве ближайшую к корню собственную выигрышную комбинацию, а также ближайшую к корню выигрышную комбинацию противника. Если выяснится, что ближайшая собственная выигрышная комбинация ближе к корню, чем выигрышная комбинация противника (человека), то следует сделать ход по той ветке, где находится эта комбинация. Если оказывается, что комбинация противника ближе – следует найти другую ветку пространства состояний, сделав ход по которой компьютер гарантированно не проиграет раньше, чем сможет выиграть или свести партию вничью.
Как видно, задание немного проще предыдущего за счёт меньшего размера пространства состояний. Но и то и другое задание не должно вызвать сложностей труда, если грамотно сделана первая работа.
Время на выполнение работы – 3 занятия.
Работа №3
Задание: решение головоломки «Восьмёрки» или «Пятнашки» с помощью «жадного» алгоритма
Всем, конечно же, известны такие древние интеллектуальные игры, как «Пятнашки» и «Восьмёрки». Особенно они известны тем, кто делал «восьмёрки» предыдущей лабораторной работой. Задачей данной работы является моделирование на компьютере ваших действий при сборе указанной головоломки с использованием так называемого «Жадного» алгоритма.
Программа должна иметь какой-то интерфейс, элементы которого позволят пользователю перемешать собранную комбинацию фишек, начать собственноручно собирать перемешанную комбинацию и в любой момент нажать на кнопку, которая вызовет функцию автоматического решения головоломки и дособерёт то, что есть. Процесс решения при этом должен отображаться на экране шаг за шагом, с отображением отходов назад, если таковые будут иметь место в процессе нахождения решения. Как видно, по функционалу задача равносильна первой задача из предыдущей лабораторной работы
Использование жадного алгоритма для «пятнашек» и «восьмёрок» аналогично, поэтому для простоты восприятия приведём пример его использовании на примере «восьмёрок». В собранном виде подобная головоломка имеет следующий вид:
 |
Задача состоит в том, чтобы собрать головоломку из некоторого произвольного состояния в целевое, указанное выше.
Смысл работы сводится к тому, чтобы из возможных вариантов каждого следующего хода выбрать наилучший. Сделать это нам (имеется в виду вам) поможет эвристическая функция следующего вида: f(n) = g(n) + h(n). В этой функции g(n) — фактическая длина пути от произвольного состояния n к начальному (то есть число ходов, которые необходимо сделать для того, чтобы прийти из начального состояния в состояние n), а h(n) — эвристическая оценка расстояния от состояния n к цели.
В самом примитивном случае значением h(n) можно считать число фишек, находящихся не на своих местах. В более продвинутом варианте этой функции учитывается также степень упорядоченности фишек друг относительно друга, что должно привести к более быстрому нахождению правильного пути. Мы рассмотрим менее продвинутый, оставив более продвинутый на самостоятельное изучение.
Приведём пример дерева, благодаря которому происходит нахождение решения из некоторого начального состояния, и поясним то, как с использованием этих данных получить решение задачи. Дерево представлено на рисунке:
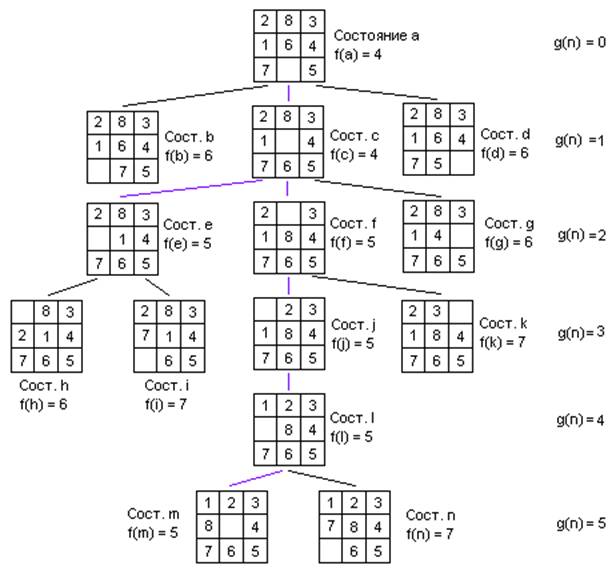
Из рисунка видно, что состояние a является начальным, а состояние m — конечным (целевым). Для удобства, каждому состоянию соответствует буква, а рядом с каждым состоянием написано посчитанное значение функции f, соответствующее текущему состоянию. Напротив каждого уровня дерева написано значение функции g(n), где n — номер хода, а следовательно и номер уровня дерева. Чем больше уровень, тем больше значение функции g(n). Обратите внимание, что при подсчёте значения функции h(n) считается только количество фишек не на своих местах. Пустое поле фишкой не считается! Например, для состояния i не на своих местах находятся фишки 1, 2, 7 и 8, поэтому значение функции h(i) будет равно 4, значение функции g(i) равно 3, а значение функции f(i) равно h(i) + g(i) = 4 + 3 = 7.
Жадный алгоритм предоставляет возможность отказаться от использования так нелюбимых студентами графов и вместо них использовать 2 списка, которые при использовании жадного алгоритма по традиции называют open и closed. Список open содержит те состояния игрового поля, которые предстоит рассмотреть для нахождения целевого решения, а список closed содержит уже рассмотренные состояния.
Изначально список open содержит лишь состояние «a», а список closed пуст. Для удобства и лучшего понимания того, что происходит, рядом с именем состояния будем писать значение оценочной функции для этого состояния. Элементы списка open должны быть упорядочены по возрастанию в соответствии со значением оценочной функции.
Итак, изначально у нас следующая картина:
open = [a4]; closed = [ ]
Состояние a в списке open не является целевым, поэтому извлекаем его из списка, меняем на те состояния, которые получаются из «a», а само состояние «a» помещаем в список уже рассмотренных состояний closed. Из состояния «a» можно получить 3 новых состояния: «b», «c» и «d». После проделанных действий содержимое списков open и closed будет следующим:
open = [c4, b6, d6]; closed = [a4]
Состояние «c» имеет наименьшее значение оценочной функции, не является целевым, значит, выигрышное состояние надо искать от него. Перемещаем его из списка open в список closed, а в список open добавляем те состояния, которые получаются из состояния «c», получаем следующие значения в списках open и closed:
open = [e5, f5, b6, d6, g6]; closed = [a4, c4]
Действуя аналогичным образом дальше, последовательно получаем следующие состояния списков open и closed:
open = [e5, f5, b6, d6, g6]; closed = [a4, c4]
open = [f5, h6, b6, d6, g6, i7]; closed = [a4, c4, e5]
open = [j5, h6, b6, d6, g6, k7, i7]; closed = [a4, c4, e5, f5]
open = [l5, h6, b6, d6, g6, k7, i7]; closed = [a4, c4, e5, f5, j5]
open = [m5, h6, b6, d6, g6, n7, k7, i7]; closed = [a4, c4, e5, f5, j5, l5]
После достижения последнего из приведённых состояний видно, что состояние «m» — целевое, а значит, задача решена. Решением будет путь, находящийся в списке closed. Обратите внимание, что использовать его просто в том виде в каком он есть не представляется возможным, поскольку нет возможности за один ход попасть, например, из комбинации «e» в комбинацию «f». Однако в комбинацию «f» можно попасть из комбинации «с», вернуться в которую из «е» можно, сделав один ход назад по списку closed.
Ваша задача — распространить этот метод (при желании) на поле размером 4 x 4 и в процессе работы со списками отображать перемещения фишек на экране для максимальной наглядности.
Задание: реализация интеллектуального противника в любой игре для двух участников с использованием процедуры минимакса
О том, что такое минимакс – всем должно быть известно из курса лекций. В качестве альтернативы к предыдущему варианту третьей лабораторной работы предлагается использовать процедуру минимакса для реализации противника в любой интеллектуальной игре на двух или более человек (например, в игре «крестики-нолики»).
Время на выполнение работы – 3 занятия.
Работа №4:
Задание: распознавание формата файла по содержимому с помощью простейшей искусственной нейронной сети
Работа посвящена овладению минимальными основами построения и обучения искусственных нейронных сетей. Сетей как таковых не будет, да и основы не очень основные, но принципы обучения нейронов данная работа должна раскрыть.
В рамках работы предлагается построить нейронную сеть, состоящую из одного нейрона и обучить её решать какую-либо простейшую задачу. В качестве такой задачи предлагается определение типа файла по его содержимому. Таким образом, перед началом работы, вам необходимо выбрать для себя один тип файла, который вы хотите распознать, заготовить чем больше тем лучше различных файлов выбранного типа и файлов типа, отличного от выбранного (например, если вы хотите распознавать, является файл файлом в формате «pdf» или нет, вам потребуется около 40 файлов в формате «pdf» и около 40 файлов не в формате «pdf»).
После выбора типа файла для распознавания можно приступать к программированию.
В рамках работы требуется создать один нейрон с 256 входами и обучить его.
Перед началом работы необходимо подготовить данные для обучения нейрона. Эти данные можно получить, обрабатывая заготовленные файлы и формируя после обработки каждого файла входной вектор. Вектор, полученный после обработки некоторого файла, должен содержать набор вероятностей появления в файле того или иного символа. Для вычисления этого вектора необходимо:
1. Посчитать, сколько раз в файле встречается символ с некоторым ASCII кодом (коды символов будут соответствовать индексу элементов массива с входными данными, а значение, расположенное по соответствующему индексу, будет соответствовать числу символов с данным кодом в данном файле)
2. Поделить значение каждого элемент массива на общее число символов файла.
В результате проделанных действий будет получен набор векторов, состоящих из 256 вещественных чисел. Векторы, полученные после обработки файлов выбранного типа, следует отличать от векторов, полученных после обработки файлов других типов, поскольку в результате поступления на вход файлов «pdf» (который мы вроде как хотим распознать) нейрон должен выдавать 1, а при поступлении других файлов -1.
После того, как входные векторы готовы, необходимо приступить к обучению нейрона. Обучение нейрона сводится к циклическому выполнению следующих действий:
1. Найти сумму произведений элементов входных векторов на элементы весового вектора:
2. Сравнить полученное значение с 0. Если значение больше 0, то подать на выход нейрона 1, иначе – подать -1.
3. Если на выходе нейрона получилось значение, которое должно получиться, то ничего не делать и перейти к рассмотрению следующего вектора.
4. Если на выходе нейрона получилось значение 1, а должно было получиться -1, то элементы вектора весовых коэффициентов (w) следует уменьшить(wi = wi - 2сxi)
5. Если на выходе нейрона получилось значение -1, а должно было получиться 1, то элементы вектора весовых коэффициентов (w) следует увеличить(wi = wi + 2сxi)
Подобную последовательность действий необходимо выполнять с данными ото всех входных файлов до тех пор, пока примерно в 90-95% случаев получаемый выход нейрона будет совпадать с желаемым. Значение «с» в приведённой выше формуле – коэффициент скорости обучения (Обычно его принимают за 0.2 или около того).
После того как сеть обучена, полученные коэффициенты следует сохранить и попробовать с их помощью определить тип 20-30 файлов, которые не участвовали в процессе обучения. Если всё хорошо, то примерно в 90% случаев результат определения будет правильный. Вот такая наука
Задание: распознавание гласных и согласных букв (чётных и нечётных цифр или чего-то подобного) с помощью простейшей искусственной нейронной сети
Если по каким-то причинам идея распознавать тип файла с помощью искусственной нейронной сети вам не нравится, её можно изменить на любую другую аналогичную задачу. Чтобы задача в итоге не оказалась слишком сложной для реализации, распознавание чего-либо следует выполнять для определения принадлежности объектов к одной из двух групп (на выходе нейрона будет значение 1 или -1). В качестве подобных задач, в частности, могут быть задачи разделения букв на гласные и согласные, цифр на чётные и нечётные. Интересной также может показаться задача разделения какого-то набора букв, например, на буквы, встречающиеся в вашем имени и буквы, которые в вашем имени не встречаются.
В каждом из случаев, перед реализацией следует задать себе вопрос о том, что будут представлять собой входные данные для обучения и сколько будет входов у нейрона. Символы для разделения можно задавать, например, в виде двумерных массивов, размерности, к примеру 8х8. Например, числа 0 и 1 можно задать следующими массивами из нулей и единиц:
- это цифра ноль!
- это цифра один!
Любые символы можно задать аналогичным образом, сделав знакоместо меньшего или большего размера. Каждый символ в этом случае следует записать в отдельный файл в виде последовательности нулей и единиц. При задании символов, обратите внимание, что они не всегда могут быть написаны идеально правильно. Отсутствие какого-то «пикселя» из 64 или присутствие неожиданного пикселя не должно (в идеале) влиять на результат распознавания.
Время на выполнение работы – 3 занятия.




