Установочные лекции по курсу «Технологии обработки Информации»
ВВЕДЕНИЕ......................................................................................................... 1
1. Виды информации и ИЗМЕРЕНИЕ ИНФОРМАЦИИ........................ 8
1.1. Определение информации............................................................... 8
1.2. Виды информации и дискретизация.................................................... 8
1.3. Хранение и передача информации. Информационная емкость........ 10
1.4. Измерение количества информации................................................... 11
1.5. Смысл меры Шенона.......................................................................... 12
2. Кодирование информации.............................................................. 13
2.1. Понятие кодирования......................................................................... 13
2.2. Кодирование для физического канала............................................... 13
3. Эффективное кодирование............................................................ 14
3.1. Что такое эффективное кодирование.................................................. 14
3.2. Статистические алгоритмы................................................................ 15
4. Помехозащищенное кодирование............................................. 20
4.1. Что такое помехозащищенное кодирование...................................... 20
4.2. Математическое описание помехозащищенного кодирования......... 22
4.3. Код Хэмминга..................................................................................... 24
4.4. Другие методы помехозащищенного кодирования........................... 30
5. Криптокодирование или Шифрование. Защита информации от несанкционированного доступа....................................... 31
6. Проблемы теории информации.................................................... 33
ВВЕДЕНИЕ
Информация! Что может быть проще информации?
Вы приступаете к изучению курса «Технологии обработки информации», далее «ТИ». По завершению, вы будет знать об информации все, необходимое для успешной профессиональной деятельности, а именно:
· что называют информацией;
· как и в чем измеряют информацию;
· что такое кодирование и задачи кодирования информации;
· методы эффективного, помехозащищенного и криптографического кодирования информации.
Но прежде всего, нам надо выяснить: ЧТО ТАКОЕ ИНФОРМАЦИЯ?
Понятие информации
Определения информации многообразны как и ее проявления. Книги, передачи по телевизору или радио, программы компьютеров и т. д. и т. п. Каждый знает: что такое информация. Но не каждый может дать определение этому термину.
В различных науках под «информацией» понимают различные сущности. Например,
· в философии — информация понимается как наши «знания» об окружающем мире, помогающие преобразовывать этот мир под свои нужды, чаще всего эти знания представляют собой различные тексты, см. рис. 1 и 2;
Ристомная «Юнлэ дадянь» — самая большая бумажная энциклопедия в истории. (http://ru. wikipedia. org/wiki/%D0%A4%D0%B0%D0%B9%D0%BB:Yongle_Dadian_Encyclopedia_1403.jpg) | Рис.2. Лексикон Техникум Харриса, титульная страница второго издания, 1708 г. (http://pages. cpsc. ucalgary. ca/~williams/Tomash%20catalog%20web/Images%20web%20site/Image%20files/H%20Images/index_3.htm) |
· в вычислительной технике — информация понимается как последовательности битов/байтов в памяти компьютера или «данные», см. рис.3;
… 00000e 47 0d 0a 1a 0ad|.PNG........IHDR| 0000000a011 90 8f |................| b641 4dd6 d8 d4 4f 58 |.....gAMA.....OX| f|2....tEXtSoftwar| 000006fd61 |e. Adobe ImageRea| 00000c9 65 3c4c|dyq. e<....PLTE""| |"VVVGGG333000BBB| 4b 4b 4b15 4f 4f 4f 2c 2c 2c 3c |KKK@@@...OOO,,,<| 3c 3c 3e 3e 3e 3a1d 1d 1d|<<>>>:99......55| d 0d 0d |5QPP777...%%%...| 000000a0a 1a 1aa 2a 2a|'''...888***... | 000000b02e 2e 2ebb bb bb| ..............|
|
Рис.3. Двоичная последовательность и шестнадцатеричное представление по 16 октетов в строке, с печатными ASCII-символами (справа) начала PNG-файла. |
· в теории систем — информация понимается как передача вещества и энергии от одной части системы к другой или «связи», см. рис.4.
|
Рис.4. Перемещение вещества и энергии в системе автоперевозок. А может этот автопоезд везет книги, т. е. информацию? |
Теория информации дает свое определение. Это определение охватывает нечто общее, что есть у всех понятий «информация». Давайте вместе разберемся, что же связывает эти понятия?
Для этого обратимся к истории.
ТИ возникла как наука, когда человечество обрело возможность обмениваться сообщениями на больших расстояниях. Т. е. вместе с возникновением телеграфа, телефона и радио. Нет, конечно и раньше человечество передавало сообщения как в пространстве (барабаны «там-там», костры на курганах и гонцы), так и во времени (наскальные рисунки, глиняные таблички и рукописи на свиной коже). Но именно с появлением массовых коммуникаций вопрос о теоретическом описании стал особенно остро, поскольку объемы сообщений сильно возросли.
Все виды «информации», перечисленные ранее, обладают одним общим свойством – это последовательности некоторых «значений».
Обратим внимание, что количество различных «значений» может сильно различаться от 2-х в двоичной последовательности, до ~40 000 иероглифов в китайском тексте и до бесконечного разнообразия значений напряжения в электрической розетке. Иными словами, общее — это то, что любая «информация» – есть функция времени. Далее мы будем называть это «сигнал».
ЧТО же мы (в теории информации) понимаем под этим словом? Давайте запомним, нам это пригодится в дальнейшем.
ИТАК: Сигнал — это любая функция, аргументом которой является время, а значением — величина, которую можно представить числом или символом.
Этот «сигнал» и есть носитель информации с точки зрения теории информации. Сама «информация» содержится в этом «сигнале» и задача теории информации определить: как измерять «информацию».
И ВОТ что важно: Главное, что следует понять — «информация» в «Теории информации» БЕССМЫСЛЕННА. Например, текст романа «Война и мир» и любое другое сочетание букв и символов, составляющих это произведение, с точки зрения теории информации несет АБСОЛЮТНО одинаковую информацию.
Для того, чтобы нам понять и разобраться в вопросе, КАК ИЗМЕРИТЬ ИНФОРМАЦИЮ, определим ПОНЯТИЕ ИНФОРМАЦИОННОГО КАНАЛА.
Понятие информационного канала
ЗАПОМНИМ: Основная операция над «сигналом», изучаемая в Теории информации — передача информации. В этом процессе важную роль играет понятие ИНФОРМАЦИОННОГО КАНАЛА.
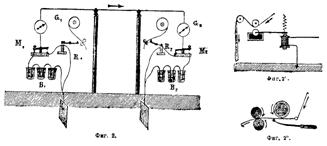
ЗАПОМНИМ: Под информационным каналом понимается любое устройство, предназначенное для передачи сигнала в пространстве или времени (см. рис.5 и рис.6).
| |
Рис.5. Передача сигнала во времени — библиотека (Региональная библиотека во французском Алансоне, построена в 1800 году http://www. lib. kture. /ru/elexh39/1.php). | Рис.5. Передача сигнала в пространстве — телеграф Морзе (Соединение двух станций посредством обыкновенного телеграфа Морзе http://upload. wikimedia. org/wikipedia/ru/2/26/). |
В этом устройстве различают три части (см. рис.7):
1) кодирующее устройство,
2) линия связи,
3) декодирующее устройство.
Источник сигнала | Кодирующее устройство | Линия связи | Декодирующее устройство | Получатель сигнала |
Рис.7. Информационный канал. |
ОПРЕДЕЛИМ ЭТИ ПОНЯТИЯ. ИТАК:
· «Кодирующим устройство» — это нечто, преобразующее сигнал в форму, допускающую передачу по линии связи.
· «Линия связи» — это нечто, способное воспроизвести переданный сигнал в другой точке пространства или времени.
· «Декодирующее устройство» — это нечто, преобразующее сигнал в первоначальную форму, т. е. в тот вид, который был получен из источника сигнала.
Например, в информационном канале «телеграф Морзе», см. рис.6, кодирующим устройством является телеграфист, преобразующий текст телеграммы в импульсы тока разной длительности; линия связи — металлический провод, по которому протекают эти импульсы; декодирующее устройство — другой телеграфист, записывающий последовательность импульсов в виде текста.
ОБРАТИМ ВНИМАНИЕ: Источник сигнала и получатель сигнала находятся вне рассмотрения ТИ – т. е. природой сигнала, а равно и его «смыслом» теория информации не интересуется.
ЗАДАДИМ СЕБЕ ВОПРОС: ЧТО ЖЕ ПРОИСХОДИТ ПРИ ПЕРЕДАЧЕ ИНФОРМАЦИИ?
ОКАЗЫВАЕТСЯ, возникают три проблемы:
· НЕОБХОДИМОСТЬ передать информацию, используя минимум ресурсов, или необходимость устранения избыточности;
· НЕОБХОДИМОСТЬ устранения случайных искажений информации при передаче (помех);
· НЕОБХОДИМОСТЬ устранения несанкционированного доступа к информации.
КАК ЖЕ РЕШАЮТСЯ ЭТИ ПРОБЛЕМЫ?
ОТВЕТ НАПРАШИВАТСЯ САМ СОБОЙ:
Эти проблемы решаются с помощью кодирования сигнала.
НО ЧТО ТАКОЕ КОДИРОВАНИЕ СИГНАЛА? ДАДИМ ОПРЕДЕЛЕНИЕ понятие кодирования и запомним. ЭТО ВАЖНО.
ИТАК:
Кодирование сигнала
Одна и та же информация (сигнал) может быть представлена в различных формах.
Преобразование информации из одной формы в другую, допускающее восстановление ИСХОДНОЙ формы информации (сигнала) без искажений — называют обратимым кодированием.
Например, текст можно записать номерами символов, а номера символов — двоичными последовательностями, см. рис.8.
|
Рис.8. Эквивалентные представления текста. |
В большинстве случаев применяется кодирование в числовое представление. Т. е. сигнал преобразуют в некую последовательность чисел. Последнее обусловлено тем, что современные устройства передачи — цифровые.
Сигнал может кодироваться с разными целями, например, для устранения избыточности, с целью записать в минимальный объем памяти или с целью борьбы с искажениями-помехами в линии связи, или для недопущения несанкционированного доступа к информации.
ЗАВЕРШАЯ НАШЕ ВСТУПЛЕНИЕ, подведем предварительные итоги.
ИТАК: В курсе Теория информации мы изучим следующие разделы
Перечень основных разделов
Во-первых, рассмотрим измерение информации и разберемся с понятием «мера Шенона»;
Во-вторых, рассмотрим теорию избыточности информации и вопросы устранения избыточности — эффективное кодирование (или сжатие данных);
В-третьих, рассмотрим теорию борьбы с искажениями и вопросы исправления ошибок — помехозащищенное кодирование;
В-четвертых, познакомимся с методами защиты информации от несанкционированного доступа — криптографией или шифрованием.
В настоящем курсе мы будем использовать в качестве основного пособия:
Лидовских информации. Учебное пособие. 2004г.
Это пособие, а также другая литература и домашние задания доступны по адресу:
mp.ustu.ru\InformationTheory
mp.ustu.ru\InformationTheory
Задать вопросы и получить консультации можно по электронной почте:
*****@
либо по телефону
.
1. Виды информации и ИЗМЕРЕНИЕ ИНФОРМАЦИИ
1.1. Определение информации
Информация — любая функция времени вида y = f(t), где t – физическое время или его аналог и y – любая величина или значение сигнала.
В качестве значения сигнала y чаще всего используется число, хотя все утверждения применимы для любых значений сигнала в виде букв, векторов, матриц, иероглифов, «пляшущих человечков» или других величин.
1.2. Виды информации и дискретизация
Информация — f(t) — может быть двух видов:
· непрерывная, рис. 9.
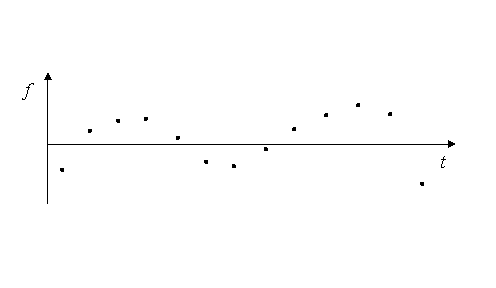
· дискретная, рис. 10.
Непрерывный сигнал
Рис. 9. |
Дискретный сигнал
Рис. 10. |
Мы будем далее рассматривать только дискретную информацию из-за более простой формы математических выражений. Но все выводы применимы и к непрерывной информации.
Дискретизация непрерывного сигнала
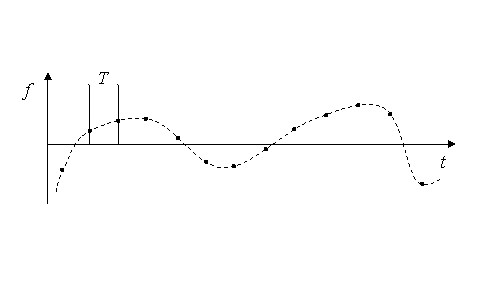
T – период дискретизации. Рис. 11. |
Непрерывная информация может быть представлен в дискретной форме (дискретизирована). Для этого достаточно замерить значения y = f(t) в моменты времени ti= i×T, где i - целое число, T – период дискретизации (рис. 11). Очевидно, что при слишком большом периоде дискретизации восстановить исходную непрерывную информацию невозможно. При уменьшении периода дискретизации до бесконечно малой величины получается практически точная копия непрерывной информации, но и количество «значений», которые надо хранить или передавать становится близким к бесконечности.
Основная теорема дискретизации: «Теорема Уиттакера — Найквиста — Котельникова — Шеннона» (или теорема Котельникова) гласит, что, если непрерывная функция f(t) имеет спектр разложения в ряд Фурье, ограниченный сверху частотой Fmax, то она может быть однозначно и без потерь восстановлена по своим дискретным отсчётам, взятым с периодом:
T £ .
Теорема сформулирована Гарри Найквистом в 1928 году в работе «Certain topics in telegraph transmission theory» и независимо в 1933 году в работе «О пропускной способности эфира и проволоки в электросвязи» и является одной из основополагающих теорем в теории цифровой связи.
Теорема также утверждает, что непрерывный сигнал можно представить в виде следующего ряда:
![]() .
.
Значения yi = f(iT) — значения дискретизированного сигнала.
Помимо чисел значениями f(t) могут быть другие величины, например, буквы текста или иные символы. Любая символьная информация — суть дискретная информация и может быть легко преобразована в числовую форму заменой символа на его порядковый номер. Например, букву можно заменить номером буквы в алфавите.
Далее будем рассматривать только дискретную информацию, т. е. некоторую последовательность чисел или символов. Такую последовательность мы будем называть: дискретная случайная величина (ДСВ).
Каждая ДСВ определяется множеством X её возможных значений x и вероятностью p(x) (или долей) каждого из значений x в ДСВ. Конкретная последовательность x1, x2… значений ДСВ называется сообщением.
1.3. Хранение и передача информации. Информационная емкость
Для хранения числовой информации могут использоваться любые устройства, способные записывать и хранить последовательности чисел.
Существует формальное математическое доказательство (см. Ноберт Винер [[1]]), что хранение чисел в двоичном представлении требует минимальных затрат энергии, т. е. наиболее «экономично».
Достаточно представить каждое число в двоичной форме и записать получившуюся цепочку нулей и единиц на носитель. Например, на перфоленту: «дырка» = 1, а «отсутствие дырки» = 0.
Абстрактный носитель, способный хранить 1 или 0, получил название «БИТ» (bit).
Поскольку придумать носитель, способный хранить меньшее чем один «БИТ» количество информации невозможно, то БИТ используется в качестве минимальной меры информационной емкости.
1.4. Измерение количества информации
Понимание того, что информационная емкость и количество информации не одно и тоже — ключевой момент.
Одна и та же информация может быть передана/записана множеством способов. Например, уменьшив период T дискретизации f(t) в два раза мы получим в два раза больше чисел для предачи/записи, но восстановленная f(t) не будет отличаться от дискретизации с периодом 2T, пока 2T меньше максимально допустимого значения (см. п. 1.2).
Это противоречие с информацией, которая равна и одновременно не равна сама себе, разрешил Клод Шенон [[2]].
Количественной мерой информации следует считать МИНИМАЛЬНУЮ информационную емкость, которая необходима для передачи (хранения) информации без искажения в условиях отсутствия помех.
Определение количественного значения минимальной информационной емкости — сложная задача. Академик [[3]] сформулировал три способа измерения количества информации:
· алгоритмический,
· комбинаторный,
· вероятностный.
Алгоритмическая мера
Можно определить меру информации, как длину кратчайшей программы, которая выводит заданную ДСВ. Поскольку, обычно, никого не интересует абсолютное значение меры, а смысл имеет только относительное измерение: «информация A» больше «информации B», то язык программы значения не имеет.
Эта мера не используется на практике, т. к. есть объективные трудности ее исчисления.
Комбинаторная мера (мера Хартли)
Если ДСВ x способна равновероятно принимать значения из множества X, состоящего из N элементов, то необходимо как минимум H(X) = log2(N) двоичных разрядов (бит), чтобы записать номер любого из возможных значений ДСВ и, соответственно, необходимо Mlog2(N) бит, чтобы записать сообщение из M конкретных значений x. Значение I(X) = log2(N) можно понимать как МИНИМАЛЬНОЕ количество бит, необходимых для записи возможных значений величины x или как меру информации, содержащейся в любом из значений x, выраженной в единицах БИТ/СИМВОЛ.
Вероятностная мера (мера Шенона)
Основное отличие от комбинаторной меры информации — постулируется неравная вероятность различных значений ДСВ X. Что это означает? Это значит, что если мы достаточно долго будем записывать некую ДСВ X, то доли конкретных значений xi в общем числе значений будут неравны.
Пусть вероятность (доля) конкретного значения xi составляет p(xi). Количество бит, необходимое В СРЕДНЕМ для записи одного значения x, может быть вычислена по формуле:
![]() . (1)
. (1)
Или необходимо не менее 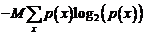 бит, чтобы записать сообщение из M конкретных значений x ДСВ X.
бит, чтобы записать сообщение из M конкретных значений x ДСВ X.
Эта формула называется формулой Шенона.
1.5. Смысл меры Шенона
Формула Шенона (1) может быть интерпретирована так: число n РАЗЛИЧНЫХ сообщений из M символов, где вероятность отдельных символов x совпадает с p(x), есть ![]() .
.
В этом смысле I(x) — есть мера неопределенности (или энтропия) ДСВ X. Указывая конкретное значение x = a, мы уничтожаем эту неопределенность, сообщая таким образом информацию ![]() на один символ сообщения.
на один символ сообщения.
Для сообщения из M значений ДСВ X величина M×I(X) равна МИНИМАЛЬНОМУ количеству бит, которое необходимо для записи этого сообщения без искажений.
2. Кодирование информации
2.1. Понятие кодирования
Кодирование (обратимое) — преобразование сигнала (информации) из одного способа записи в другой, допускающее восстановление первоначальной записи без искажений.
Кодирование производится с целями:
1) обеспечить возможность передачи информации;
2) увеличить скорость передачи информации;
3) защитить информацию от искажений.
4) защитить информацию от несанкционированного доступа;
Первая цель возникает, когда сигнал имеет природу, не допускающую передачу этого сигнала через информационный канал. Например, исходный сигнал — рукописный текст, а канал — медный провод. В этом случае необходимо преобразовать текст в электрические импульсы. Этот тип кодирования называют: «кодирование для физического канала».
Вторая цель возникает когда пропускная способность канала недостаточна для передачи сигнала и желательно максимально уменьшить количество передаваемых бит. В этом случае необходимо перекодировать сигнал в более экономное с точки зрения количества бит представление. Этот тип кодирования называют «эффективным кодированием» или «сжатием информации».
Третья цель возникает при передаче сигнала через канал с помехами. Необходимо предотвратить искажение информации или, как минимум, обнаружить искажение, если уж оно произошло. Этот тип кодирования называют «помехозащищенным кодированием».
Четвертая цель возникает когда необходимо передавать конфиденциальную информацию по общедоступным (открытым) каналам. Желательно перекодировать информацию в вид, который не позволит прочитать информацию лицам на то не уполномоченным. Этот тип кодирования называется «шифрование».
2.2. Кодирование для физического канала
В курсе теории информации мы не будем подробно рассматривать этот тип кодирования. Ограничимся самыми общими замечениями.
Способы кодирования информации к форме, допускающей передачу через канал, зависят от физической природы канала. Так например, если каналом служит металлический проводник — информация должна быть перекодирована в электрические импульсы, если канал — оптоволокно — в импульсы света, если канал — бумага — в печатные/рукописные символы и т. д. и т. п.
Природа канала накладывает ограничения и на способ передачи этого сигнала. Так, например, при передаче электрических сигналов через проводник не используется кодировка типа: есть напряжение = 1, нет напряжения = 0. Это обусловлено техническими трудностями детектирования постоянного уровня напряжения, оказывается, что гораздо проще и надежнее детектируется изменение напряжения и, как следствие, большинство систем кодирования электрических импульсов кодирует 0 как отсутствие изменения напряжения, а 1 как изменение напряжения в проводнике. Сходные особенности характерны и для других видов каналов.
Для современных цифровых каналов характерна и некоторая общность «кодирования для физического канала» — любой сигнал переводится в цифровую форму.
Например, тексты преобразуют в последовательности чисел, согласно некоей кодировочной таблицы (ASCII, UNICODE и т. п.).
Кодировочная таблица сопоставляет каждому символу целое число. Обычно, количество чисел и символов есть целая степень двойки, так ASCII имеет 28 = 256 различных символов, Unicode — 216 = 65536 символов. Кодировочные таблицы позволяют записать любую символьную информацию как последовательность целых чисел фиксированной битовой ширины (см. рис.8), т. е. перевести любую информацию в цифровую форму.
3. Эффективное кодирование
3.1. Что такое эффективное кодирование
Измерение информации не имело бы никакого смысла, если бы на практике было невозможно записать информацию в указанное формулой Шенона (1) число бит. Но для этого необходимо кодирование информации, т. е. преобразование ее к другой — краткой форме записи.
Раздел «эффективное кодирование» как раз изучает способы генерации кодовых таблиц для краткой записи информации при условии возможности восстановить информацию в исходном виде без искажений.
Алгоритм Running
Один из самых простых алгоритмов сжатия —алгоритм Running или RLE (Run Length Encoding). Пусть имеется сообщение из одинаковых символов. Налицо явная избыточность информации. По Шенону, кстати, количество информации в таком сообщения и вовсе равно нулю. Эффективное кодирование осуществляется следующим образом:
1) подсчитываем количество одинаковых символов в цепочке;
2) вместо цепочки одинаковых символов записываем, символ и число — сколько раз повторяется этот символ.
Например, строка из 40 «А»: «АААААААААААААААААААААААААААААААААААААААА». Записываем: «А40». Строка длиной 40 символов сжимается до трех символов.
Алгоритм феноменально прост, но малоэффективен. Существует информация, которая содержит повторяющиеся символы, но не может быть сжата этим алгоритмом. Например, когда повторяется не символ, а последовательность символов. Например: «АБАБАБАБАБАБ». Повторяющихся символов нет, и сжать нельзя. Можно, конечно, воспользоваться расширенным алгоритмом:
1) ищем не повторяющиеся символы, а повторяющиеся последовательности символов (в данном случае это «аб»);
2) подсчитываем, сколько раз повторяется эта последовательность;
3) записываем количество повторяющихся фрагментов (в нашем случае 6), и сам фрагмент (в нашем случае «АБ»): «6,АБ».
Но и это не предел. Могут существовать одинаковые фрагменты информации, располагающиеся в разных местах файла. Можно найти эти фрагменты. Записать в кодовую таблицу и приписать каждому определенное значение — код. После этого можно заменит все фрагменты этим кодом-ссылкой.
Несмотря на простоту идеи — реализация такого алгоритма — весьма непростая задача.
Существуют особые ситуации, когда поиск повторяющихся фрагментов может быть ускорен. Например, при передаче видеоизображения данные представляют собой последовательность кадров-картинок, состоящих из массива точек. Эти картинки имеют одинаковый размер и часто предыдущая картинка слабо отличаются от последующей (простейший пример, снимается неподвижный объект). В этом случае реализация Running-подобного алгоритма проста — записывать для каждого следующего кадра только его отличия от предыдущего и можно добиться существенного сжатия данных для медленно меняющихся изображений.
Алгоритмы, подобные RLE, называют алгоритмами корреляционного анализа — эти алгоритмы ищут зависимости (корреляции) между отдельными участками информации и заменяют найденное ссылкой на предыдущее (первое) вхождение подобного участка. К этим алгоритмам мы еще вернемся.
Существуют алгоритмы и другой природы.
3.2. Статистические алгоритмы
Статистические алгоритмы обрабатывают информацию «посимвольно», т. е. предлагают такой способ кодирования для каждого символа, чтобы запись сообщения требовала бы минимальной информационной емкости (минимального числа бит).
Формула Шенона (1) играет определяющую роль для этих алгоритмов. Количество информации по Шенону = минимальному количеству бит НЕОБХОДИМЫХ для записи этой информации. Т. е. формула Шенона устанавливает абсолютный нижний предел.
Идея статических алгоритмов проста. Если информация — последовательность чисел, фиксированной битовой длины (символов), и частота, с которой различные числа присутствуют в этих данных, различается, то заменив битовые цепочки фиксированной длины на битовые цепочки различной длины, так, чтобы более часто встречающимся числам (символам) соответствовали бы более короткие цепочки, можно получить уменьшение объема данных.
Алгоритм Хаффмана
Алгоритм Хаффмана — это способ построения эффективного (минимального) кода. Будем предполагать данные последовательностью байт (8-и битных кусочков). Это необязательно, можно применять алгоритм Хаффмана к битовым цепочкам любой фиксированной длины.
Рассмотрим пример: пусть имеются данные длиной в 100 байт, включающие шесть различных чисел: 1, 2, 3, 4, 5, 7.
Первое, что необходимо сделать — это подсчитать сколько раз встречается каждое число в данных — вычислить p(xi) .
После подсчета количества вхождений каждого символа мы получаем таблицу частот (рис. 12). Таблица имеет ненулевые значения количества вхождений для чисел 1, 2, 3, 4, 5, 7. Ячейки таблицы будем называть «узлами».
Таблица частот (исходная таблица) метода Хаффмана
Рис. 12. |
Найдем в таблице наименьшие ненулевые количества вхождений. Для этого удобно отсортировать таблицу по возрастанию (рис. 13). В нашем случае это 5 и 10 для узлов 4 и 1. Сформируем из узлов 4 и 1 новый узел, количества вхождений для которого будет равно сумме количества вхождений исходных узлов, рис. 13. Объединенные узлы 4 и 1, более не участвуют в создании новых узлов.
Формирование первого узла в методе Хаффмана
Рис. 13. |
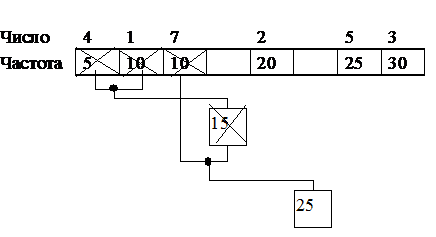
Новый узел и оставшиеся узлы таблицы частот образуют новую таблицу, для которой повторяют операцию добавления узла. Самая низкая частота 10 (узел 7) и 15 (новый узел). Снова добавим узел, см. рис. 14.
Продолжаем добавлять узлы, пока не останется единственный узел, рис. 15. Структура на рис. 15, где каждый нижележащий узел имеет связь с двумя вышележащими узлами носит название «двоичное дерево».
Формирование второго узла в метода Хаффмана
Рис. 14. |
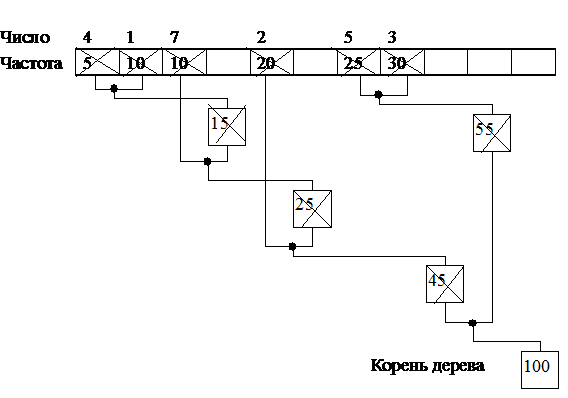
Дерево узлов в методе Хаффмана
Рис. 15. |
Теперь, когда дерево выращено, можно вычислить коды. Вычисление кода исходного числа/символа начинается от корня дерева. Для вычисления кода, двигаясь по дереву от корня к исходному числу/символу, надо записать все повороты в точках объединения узлов. Если поворот в узле осуществляется налево, то в цепочке битов устанавливается значение 0, если направо — 1. Можно наооборот.
Например, для числа 3 от корня до исходного узла пройдем два узла, т. е. длина кода два бита. Первый от корня поворот направо 1 и второй тоже направо 1 => код Хаффмана для числа равен 11b.
Выполнив вычисление для всех чисел, получим следующие коды Хаффмана:
1. ® 0111b (4 бита );
2. ® 00b ( 2 бита );
3. ® 11b ( 2 бита );
4. ® 0110b ( 4 бита );
5. ® 10b ( 2 бита );
7. ® 010b ( 3 бита
Каждый символ изначально представлялся 8-ю битами, и так как мы уменьшили число битов необходимых для представления каждого символа, мы, следовательно, уменьшили размер выходного файла. Результирующее сжатие может быть вычислено следующим образом, см. табл. .
Таблица 1
Вычисление степени сжатия даных
Число | Число вхождений | Первоначальный размер, бит | Уплотненный размер, бит | Уменьшение размера, бит |
1. | 10 | 80 | 40 | 40 |
2. | 20 | 160 | 40 | 120 |
3. | 30 | 240 | 60 | 180 |
4. | 5 | 40 | 20 | 20 |
5. | 25 | 200 | 50 | 150 |
7. | 10 | 80 | 30 | 50 |
ВСЕГО | 100 | 800 | 240 | 560 |
Первоначальный размер данных: 100 байт или 800 бит; размер сжатых данных: 30 байт или 240 бит; так что получили размер данных 0,3 исходного. Заметим, что в той же пропорции же будет уменьшен размер данных для более длинного сообщения, если частотные характеристики не изменятся.
Для восстановления данных, необходимо иметь декодирующее дерево. Следовательно, необходимо сохранить дерево вместе с данными. Это увеличивает размеры сжатых данных. Если для ссылок на узлы использовать номер узла, то такой номер может изменяться от 0 до 511 (для байта), т. е. для хранения ссылки необходимо 9 бит. В рассмотренном примере дерево состоит из 5 узлов по две ссылки (18 бит), итого 90 бит необходимо для сохранения информации по дереву.
Более корректный подсчет степени сжатия: первоначальный размер данных: 100 байт или 800 бит; размер сжатых данных 240 бит и 90 бит данных о дереве — суммарный размер данных 0,41 исходного.
Метод Хаффмана не всегда способен уменьшить размер данных. Очевидно, что для данных, где встречаются все числа (0¸255) и частоты их равны, получится длина кода для каждого числа 8 бит и никакого сжатия.
Невозможность сжать данные по алгоритму Хаффмана не означает отсутствие возможности сжатия вообще. Например, очевидно, что любая последовательность, где встречаются все байты (0..255) с равными частотами несжимаема по Хаффману. Но, если числа в данных расположены группами состоящими из одинаковах чисел, например: 1,1,1,1,7,7,7,7 и т. д., то такие данные легко сжать методом Running.
Вопрос о избыточности информации в общем случае не решен.
Другие алгоритмы сжатия
Существует не так уж много эффективных алгоритмов сжатия. Можно отметить такие статистические алгоритмы:
· алгоритм Шенона-Фано;
· алгоритм Хаффмана;
· арифметическое сжатие.
Это все, что известно из области статистических алгоритмов.
Из корреляционных алгоритмов можно отметить:
· алгоритмы группы Лемпеля-Зива — это целое семейство алгоритмов, объединенных общей идеей поиска и замены повторов участков сигнала на предыдущие вхождения этих участков. Являются развитием идей RLE.
· контекстные методы — методы пытающиеся построить модель данных. И определить параметры этой модели. После чего данные заменяются на параметры модели, которая позволяет восстановить данные в исходной форме. Можно понимать эти методы как попытку построить формулу F(i), где i – номер символа, так чтобы F(i) = правильному символу для всех i. Среди реально существующих контекстных методов можно указать метод «предсказание по частичному совпадению» (PPM).
Подробнее с этими и другими методами сжатия можно ознакомиться на сайте «*****».
Основными проблемами создания эффективных алгоритмов сжатия является: 1) быстродействие алгоритма; 2) размер кодирующей/декодирующей программы.
4. Помехозащищенное кодирование
4.1. Что такое помехозащищенное кодирование
При передаче/хранении информации, она подвергается воздействию неконтролируемых факторов внешней среды. Результатом такого воздействия может быть искажение информации.
Помехозащищенное кодирование изучает возможности представления (перекодировки) информации в форму обеспечивающую
1) обнаружение искажений в переданной информации — как минимум;
2) исправление ошибок в переданной информации — как максимум.
Очевидно, что это может быть достигнуто только за счет передачи добавочной информации. В отличие от предыдущих типов кодирования, оставлявших битовый размер информации неизменным или уменьшавшими размер, методы помехозащищенного кодирования всегда увеличивают размер передаваемой информации.
Основная задача — использовать добавочную информацию как можно эффективнее, т. е. максимизировать вероятность обнаружения/исправления ошибки на каждый дополнительный бит.
Следует понимать — не существует методов, дающих абсолютную гарантию обнаружения ошибки.
Известно не так уж много эффективных методов помехозащищенного кодирования.
Блочное кодирование
На практике помехозащищенное кодирование часто применяют к порциям данных (информации) фиксированной длины. Такие порции бит называют: блоки. А сами методы помехозащищенного кодирования, использующие блоки: блочным кодированием. Длина исходного блока в битах обозначается n. Алгоритмы помехозащищенного кодирования добавляют фиксированное число бит к исходному блоку, получая блок из m бит. Блочный код обозначают: код (n, m).
Существуют и неблочные методы помехозащищенного кодирования.
Коды обнаружения ошибок
Методы помехозащищенного кодирования направленные только на обнаружение ошибки называют – коды обнаружения ошибок. Обнаружение ошибки позволяет, в некоторых ситуациях, перезапросить данные с источника и исправить ошибку. Ну или не использовать ошибочные данные. Поскольку коррекция ошибок в этих методах не требуется, то размер дополнительно передаваемой информации минимален.
Простейшим кодом обнаружения ошибок является «контроль четности». В этом случае, все сообщение разбивается на блоки бит равного размера, например, по 8-мь бит. И вычисляется сумма значений бит каждого из этих блоков. К блоку добавляется еще один бит: если сумма нечетная, то бит 1, иначе — бит 0. Т. е. получается блок длиной а один бит больше исходного — это «бит четности». При получении данных вычисление «бита четности» повторяется и результат сравнивается с переданным битом четности. Если вычисленное и переданное значение «бита четности» совпадают, то значит ошибки не было, иначе — ошибка передачи.
Легко сообразить, что искажение двух, четырех и любого четного количества бит в блоке не будет обнаружено.
Однако, в силу своей простоты, метод широко применяется в информационных каналах, где вероятность ошибки мала. Данный метод позволяет легко регулировать избыточность данных, выбирая размер блока. Чем больше исходный блок — тем меньше относительный размер дополнительной информации и тем выше вероятность пропустить ошибку.
Другим примером кодов обнаружения ошибок является «циклическая сумма» (Cyclic Redundancy Checksum или CRC). Этот метод является неблочным, но может быть использован и в блочном варианте. Принцип обнаружения ошибки схож с кодом «контроля четности». Используя особый алгоритм суммируются значения всех битов данных или порции данных, в результате суммирования получается некое число (не один бит, а несколько), которое передается вместе с данными или порцией данных. Принимающая сторона вычисляет CRC повторно и сравнивает с переданным.
«Контроль четности» — частный случай CRC. Алгоритм CRC вы сможете изучить на практических занятиях.
Корректирующие коды
Корректирующие коды — коды, служащие для обнаружения и исправления ошибок, возникающих при передаче информации под влиянием помех.
Для этого при передаче к исходной информации добавляют дополнительную информацию. Т. е. из исходного блока длиной n, делают блок длиной m, где m > n.
Приемник повторно вычисляет эту дополнительную информацию и сравнивает ее с переданной. На основании различий делается вывод о наличии или отсутствии ошибок. При обнаружении ошибок выполняется корректирующее действие.
Одним из самых простых, но неэффективных, способов коррекции является тройное мажорирование. Тройное мажорирование состоит в том, что данные (каждый бит или каждый блок битов) передаются три раза, а на приёмной стороне производится простое голосование по трём принятым значениям бита. Например, если требуется передать «1», то в канал связи поступит «111». В результате искажений может быть принято, например, «101», а после голосования получится «1» (так как в строке «101» единиц больше чем нулей). Однако искажение двух битов (например, принято «100», вместо «111») никогда не будет обнаружено и исправлено.
Надежность тройного мажорирования оставляет желать лучшего, ибо при некоторых типах информационных линий и некоторых типах ошибок обнаружить ошибку невозможно. Например, линия из 8-и проводов передает по 8-мь бит за такт (по одному через каждый провод). Если один из проводов оборван — эта ошибка никогда не будет обнаружена тройным мажорированием.
Другой существенный недостаток этого метода — перегрузка канала связи — передается в три раза больше бит, чем необходимо.
4.2. Математическое описание помехозащищенного кодирования
Чтобы описывать и сравнивать эффективность методов помехозащищенного кодирования нужна модель канала и ошибок в нем. Очевидно, что реальные каналы весьма разнообразны и описать их сразу все невозможно. Но и не имея модели — тоже ничего не сделать.
Решением этой проблемы служит простая модель «двоичного симметричного канала» и понятие «расстояние между двумя двоичными блоками».
Двоичный симметричный канал
Модель двоичного симметричного канала – простейшая модель канала с ошибками. Предполагается
1. Биты передаются по каналу последовательно — один за другим. Единомоментно передается только один бит, поэтому канал и называется двоичным.
2. Независимо от значения бита (0 или 1) вероятность его искажения постоянна и равна q. Поэтому канал называется симметричным.
Расстояние между битовыми блоками. Метрика Хемминга
Расстоянием Хемминга d(x1, x2) (метрикой Хемминга) между двумя битовыми блоками одинаковой длины x1 ={b1, b2, …bn} и x2 ={с1, с2, …сn} называется количество отличающихся бит на соответствующих позициях блока. Расстояние между абсолютно одинаковыми битовыми блоками равно нулю. Изменение одного бита в любом блоке увеличивает это расстояние на 1.
Очевидно, что расстоянием Хемминга между полученным и отправленным блоком можно характеризовать степень искажения информации.
Минимальное кодовое расстояние и корректирующая способность
Очевидно, что приемник не может сравнить полученный и отправленный блок. Если это возможно — значит приемнику известно точное значение отправленного блока. Если так — проблема искажений отсутствует.
Важно понять очевидную истину: обнаруживать и исправлять ошибки можно и нужно опираясь только на полученный блок данных. И ничего не зная про содержание отправленного.
Если передатчик использует ВСЕ возможные значения двоичного блока длиной m, то приемник не может обнаружить ошибку, ведь все значения блока допустимы. Однако закодированный двоичный блок длиной m может принимать 2m различных значений, а исходный блок длиной n < m имеет 2n различных значений. Т. е. 2m - 2n значений являются недопустимыми или лишними. Дополнительные m - n бит являются избыточной информацией.
Только получив недопустимое значение блока, приемник может обнаружить ошибку.
Избыточные биты желательно использовать так, чтобы обнаруживать и исправлять максимальное число ошибок. Здесь надо понимать — невозможно создать абсолютно помехозащищенный код. Всегда существует возможность такого искажения блока, что будет получено другое допустимое значение блока. Однако, желательно обеспечить максимальный эффект от «дополнительных» бит.
«Эффект» дополнительных бит проще всего определить как минимальное количество ошибок в блоке, которые код гарантированно может обнаружить и исправить. Чем больше это число – тем лучше используются дополнительные биты.
Эффективность блочного кода называется «корректирующей способностью кода». Корректирующая способность блочного кода определяется минимальным расстоянием Хемминга dmin между двумя допустимыми значениями блока кода.
Корректирующая способность t = [(dmin - 1)/2] определяет минимальное количество ошибок t в блоке кода, которое можно обнаружить и исправить, здесь […] обозначает взятие целой части.
Идеальным случаем является dmin = dmах, т. е. когда минимальное и максимальное расстояние между допустимыми значениями блоков равно. Тогда корректирующая способность максимальна, а избыточность данных минимальна. Такие коды называют «совершенными».
Совершенные коды
Известно всего два совершенных кода. Это код Хэмминга и код Голея (12, 24), исправляющий 8 ошибок на блок. Более точно, код Хэмминга — это группа совершенных кодов с dmin = 3.
4.3. Код Хэмминга
Коды Хемминга —линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку на блок.
Достоинство кода в том, что реализация алгоритма требует небольших ресурсов и может быть выполнена аппаратно.
Исходными данными для кодирования является произвольная двоичная последовательность, например как это изображено на рис. 16
Исходная битовая последовательность
№ бита | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | … | n |
значение бита | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
Рис. 16.
Кодирование по Хэммингу
Прежде всего, двоичная последовательность делится на блоки размером в n бит. Размер исходных блоков не произволен, их длина определяются формулой
n = 2r ‑ r - 1,
где r – любое целое число, большее 2. Эти блоки будем называть «блоки исходного кода» и обозначать ai.
Положим для определенности r = 4, тогда n = 11. Блоки исходного кода изображены на рис. 17.
Разделение битовой последовательности на блоки исходного кода
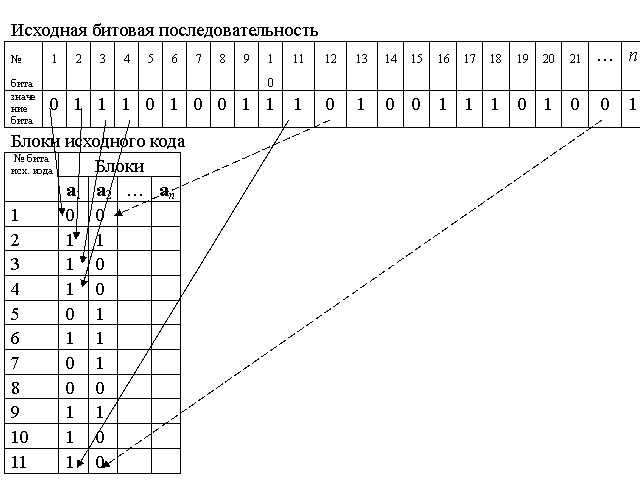

Рис. 17.
Далее исходные коды расширяют до m бит каждый, дополняя r контрольными битами. Полученные m-битные коды образуются так:
· Позиции с номерами 2i (i = 1, 2, …r) резервируются под контрольные биты;
· в остальные биты копируется исходный код в порядке следования его битов.
Расширенные блоки будем называть «блок кода» и обозначать bi. Расширение исходного кода для r = 4 и n = 15 продемонстрировано на рис. 18.
Расширение блоков исходного кода контрольными разрядами
|


Рис. 18
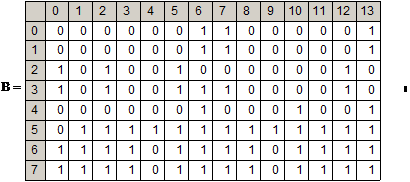
Затем вычисляют контрольные разряды. Для вычисления нужна вспомогательная матрица M размером (2r – 1) строк и r столбцов. Матрица заполняется по строкам, в каждую строку записывают двоичное представление чисел от 1 до 2r – 1, младшие биты пишут ПЕРВЫМИ. Такая матрица для r = 4 показана на рис. 19. Далее вычисляются контрольные разряды ci, для этого из матрицы M выбираются и побитно суммируются все строки, номера которых совпадают с номерами ненулевых бит блока кода bi. Полученная строка из r битов записывается в контрольные разряды блока кода bi в порядке следования битов, как показано на рис.19.
Вычисление контрольных разрядов ci можно представить матричным умножением
ci = (bi)T×M,
здесь (bi)T — строка-блок расширенного кода, где контрольные биты равны 0.
Блоки кода можно вновь преобразовать в последовательность бит и передавать по каналу связи.
Код Хемминга способен детектировать и исправлять 1 (одну) ошибку на блок.
Вычисление контрольных разрядов
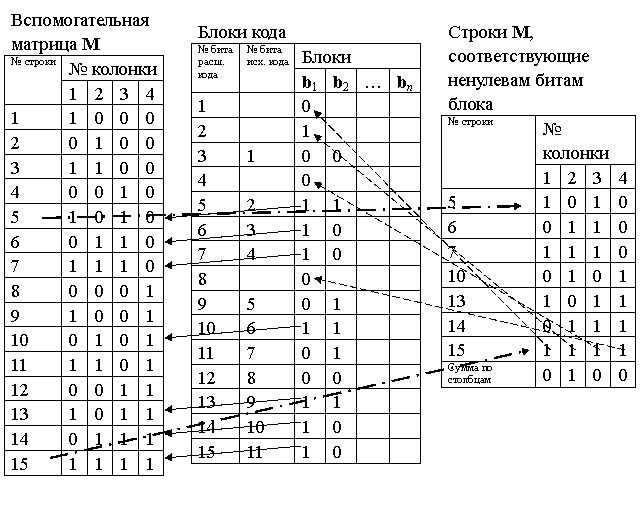

Рис. 19.
Декодирование и исправление ошибки по Хэммингу
Переданная по информационному каналу в приемник битовая последовательность делится на блоки по n = 2r - 1 бит — получаются блоки кода. С каждым таким блоком выполняется операция
ci = (bi)T×M,
здесь (bi)T — строка расширенного кода. Пример приведен на рис. 20. Причем здесь значения контрольных разрядов участвуют в вычислении суммы.
Если все биты ci равны нулю, то ошибок нет и коррекция не нужна, см. рис. 20.
Если хотя бы один бит ci не равен нулю (см. рис. 21), то была ошибка. Значение ci преобразуют из битового представления в десятичное число i и бит блока кода с номером i — ошибочный бит. Для исправления значение бита инвертируют: заменяют ноль на единицу, а единицу на ноль. В результате получаем правильное значение блока кода.
Проверка на ошибки — нет ошибок
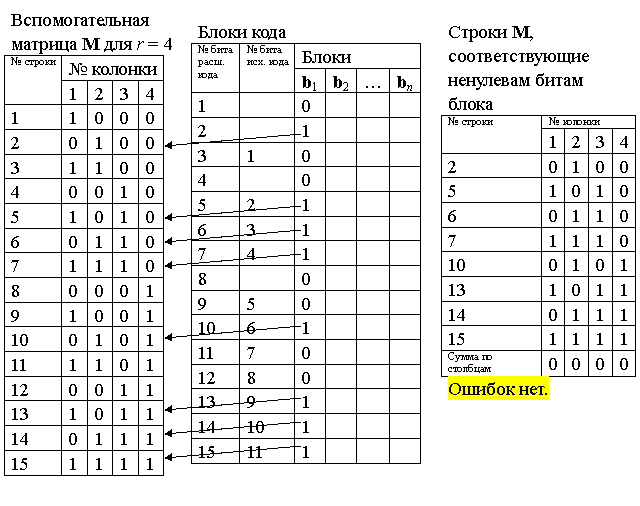

Рис. 20.
В заключение, контрольные разряды удаляются из блока и получается блок исходного кода. Эту операцию (проверка-коррекция) проводят с каждым блоком кода.
Невозможность коррекции двойных ошибок и ошибок большей кратности
Две и более ошибки в блоке кода Хэмминга невозможно исправить. Невозможно отличить ошибку в одном бите и ошибку в двух и более битах.
Невозможность исправления двойной ошибки следует и простого факта – процедура коррекции вычисляет номер ошибочного бита. Следовательно, второй ошибочный бит просто невозможно указать. Пример двойной ошибки приведен на рис. 22.
Проверка на ошибки и коррекция ошибок
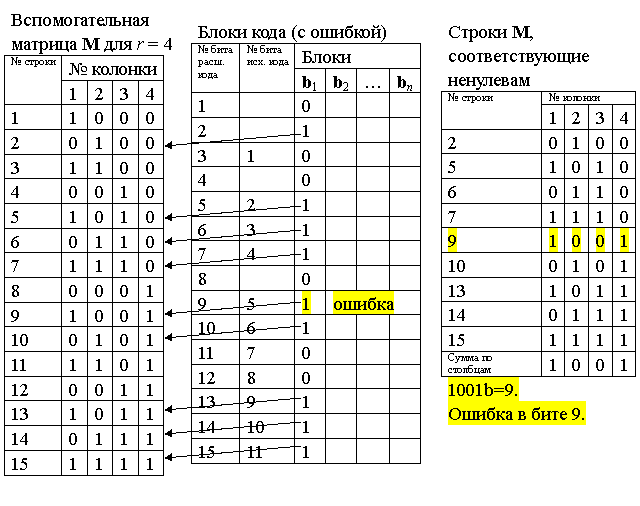

Пусть 9-й бит передан неправильно, см. рис. 20. Как видно, сумма строк вспомогательной матрицы дает номер бита с ошибкой.
Рис. 21.
Недостатки кода Хэмминга
Недостаток кода Хэмминга — некратность размера исходного блока кода и блока кода степени двойки. Это затрудняет обработку кодов Хэмминга на компьютерах, оперирующих блоками бит кратными степени двойки (8, 16, 32, 64 бит и т. д.).
Другим важным недостатком является невозможность создать код для исправления двойных ошибок или ошибок большей кратности.
Проверка на ошибки и невозможность коррекции ошибок кратности два и выше
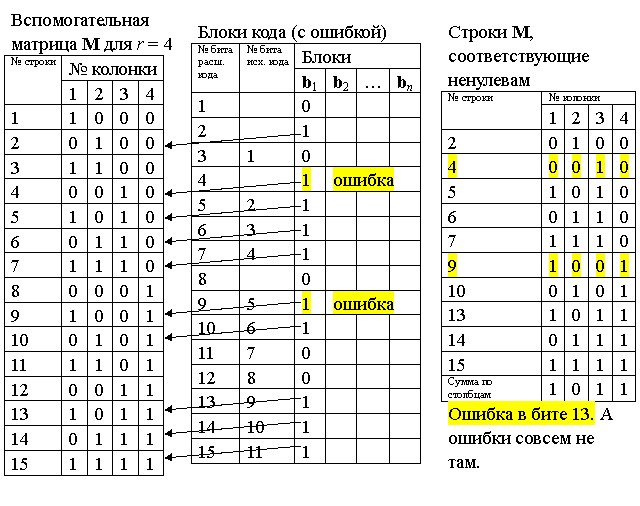

Рис. 22.
4.4. Другие методы помехозащищенного кодирования
Поскольку (и это доказано) других совершенных кодов, кроме кода Хэмминга и кода Голея не существует, то практически используются «квазисовершенные» коды. Т. е. коды «почти» совершенные.
Среди этих кодов можно упомянуть:
· Коды БЧХ (Боуза — Чоудхури — Хоквингема);
· Коды Рида — Соломона (недвоичные коды БЧХ).
Познакомиться с кодами БЧХ вы сможете на практических занятиях.
5. Криптокодирование или Шифрование. Защита информации от несанкционированного доступа
Рассмотренные ранее типы кодирования решают объективные проблемы предачи информации. К сожалению существуют и другие потребности.
Современное общество является антагонистическим обществом — т. е. обществом основанном на противоречиях и конкуренции индивидуумов или групп индивидуумов. Мы не будем исследовать причины этого, рассмотрим только следствие.
Следствием антагонизмов в обществе является потребность ограничения доступа к информации неким кругом «допущенных» лиц, при сохранении возможности передавать эту информацию по открытым (незащищенным) информационным каналам.
Открытость канала означает, что данные (биты и байты) передаваемые через этот канал доступны неопределенному кругу лиц.
Ограничение доступа означает, что никто не может получить исходный вид информации, кроме избранного круга лиц.
Для защиты данных от нежелательного доступа используют методы криптографического кодирования или шифрование.
Систему передачи защищенной от несанкционированного доступа информации по открытым каналам называют: криптосистемой.
Лиц, допущенных к информации внутри криптосистемы, называют абонентами криптосистемы.
Задача любой криптосистемы — сделать из осмысленной информации абсолютно бессмысленную, на первый взгляд, информацию. Но с одним важным свойством — если вы «допущены», то не представляет большого труда вернуть информацию к ее исходному виду и, наоборот, если вы «НЕдопущены» — то восстановление исходного вида информации становится сложной, а в идеале — неразрешимой задачей.
Криптокодирование стоит особняком среди других типов кодирования. В криптографии учитывается, что информация имеет смысл.
Современные системы криптопреобразования состоят из двух частей:
1) Алгоритм криптопреобразования. Алгоритмы кодирования всех современных криптосистем являются открытыми, т. е. каждый может с ними ознакомиться.
2) Ключ — параметр криптопреобразования, используемый для выполнения конкретной операции криптокодирования данных. Ключ выбирается абонентами криптосистемы из множества допустимых значений ключей и является тем самым «допуском» к информации. Зная ключ — можно легко выполнить обратное криптопреобразование и получить доступ к информации.
Алгоритм криптопреобразования допускает использования огромного числа различных ключей и не дает возможности по каким-либо признакам зашифрованной информации определить ключ. Как следствие, несанкционированный доступ становиться чрезвычайно затрудненным, ибо злоумышленнику надо перебрать все возможные ключи — т. е. выполнить гигантское количество вычислительных операций чтобы найти нужный ключ. Современные криптосистемы обещают временные затраты на подбор ключа порядка 50‑100 лет при использовании самых быстродействующих вычислительных машин из доступных в настоящее время.
Почему сам алгоритм шифрования делают общедоступным? Причины две:
1) Использование криптопреобразования в современных информационных системах требует внедрения алгоритма в самые разные программы, которые пишут самые разные люди, как следствие, либо алгоритм публичен, либо он станет публичным после ознакомления с ним неопределенного круга лиц «программописателей», либо алгоритм не будет использоваться.
2) Криптография (наука о криптопреобразованиях) не может ДОКАЗАТЬ стойкость того или иного алгоритма. Только ТЕСТИРОВАНИЕ на практике и в возможно более широком круге дает некоторые гарантии качества алгоритма.
На настоящий момент выделяют два типа криптоалгоритмов:
1) Алгоритмы с симметричным ключом, они же — симмметричные криптоалгоритмы.
2) Алгоритмы с несимметричным ключом, они же — несимметричные криптоалгоритмы.
Симмметричные криптоалгоритмы используют один и тот же ключ для шифрования и дешифрования. Это самые старые, из известных человеку, типов криптоалгоритмов. Самые ранние упоминания о них восходят к времени изобретения письменности.
Современные симметричные криптоалгоритмы (ГОСТ , AES и др.) обладают высокой скоростью преобразования и хорошей криптостойкостью (устойчивостью к взлому). Главный недостаток симметричных криптоалгоритмов — необходимость обмена ключом между абонентами криптосистемы. Ключ необходимо передать через защищенный канал связи, чтобы исключить возможность перехвата.
Этого недостатка лишены новейшие (их изобретение датируется 1976 годом) асимметричные криптоалгоритмы (RSA и т. п.). В этом типе криптопреобразований используется два ключа, одним можно только зашифровать сообщение (открытый ключ), другим — только расшифровать сообщение (закрытый) ключ. В этом случае абоненты криптосистемы могут обменяться открытыми ключами через незащищенный канал связи. Недостатком несимметричных алгоритмов является их меньшее, по сравнению с симмметричными, быстродействие.
Рассматривать здесь описание конткретных криптоалгоритмов мы не будем — это довольно громоздко. С описанием и работой некоторых криптоалгоритмов можно будет в ходе выполнения лабораторных работ по курсу.
6. Проблемы теории информации
БАНДВАГОН 1)
(Перепечатка из книги: Работы по теории информации и кибернетике
(перевод с английского, под редакцией и ). –
М.: Изд. иностр. лит., 1963. – С. 667-668.)
За последние несколько лет теория информации превратилась в своего рода бандвагон от науки. Появившись на свет в качестве специального метода в теории связи, она заняла выдающееся место как в популярной, так и в научной литературе. Это можно объяснить отчасти ее связью с такими модными областями науки и техники, как кибернетика, теория автоматов, теория вычислительных машин, а отчасти новизной ее тематики. В результате всего этого значение теории информации было, возможно, преувеличено и раздуто до пределов, превышающих ее реальные достижения. Ученые различных специальностей, привлеченные поднятым шумом и перспективами новых направлений исследования, используют идеи теории информации при решении своих частных задач. Так, теория информации нашла применение в биологии, психологии, лингвистике, теоретической физике, экономике, теории организации производства и во многих других областях науки и техники. Короче говоря, сейчас теория информации, как модный опьяняющий напиток, кружит голову всем вокруг.
Для всех, кто работает в области теории информации, такая широкая популярность несомненно приятна и стимулирует их работу, но такая популярность в то же время и настораживает. Сознавая, что теория информации является сильным средством решения проблем теории связи (и в этом отношении ее значение будет возрастать), нельзя забывать, что она не является панацеей для инженера-связиста и тем более для представителей всех других специальностей. Очень редко удается открыть одновременно несколько тайн природы одним и тем же ключем. Здание нашего несколько искусственно созданного благополучия слишком легко может рухнуть, как только в один прекрасный день окажется, что при помощи нескольких магических слов, таких, как информация, энтропия, избыточность..., нельзя решить всех нерешенных проблем.
Что можно сделать, чтобы внести в сложившуюся ситуацию ноту умеренности? Во-первых, представителям различных наук следует ясно понимать, что основные положения теории информации касаются очень специфического направления исследования, направления, которое совершенно не обязательно должно оказаться плодотворным в психологии, экономике и в других социальных науках. В самом деле, основу теории информации составляет одна из ветвей математики, т. е. строго дедуктивная система. Поэтому глубокое понимание математической стороны теории информации и ее практических приложений к вопросам общей теории связи является обязательным условием использования теории информации в других областях науки. Я лично полагаю, что многие положения теории информации могут оказаться очень полезными в этих науках; действительно, в ней уже достигнуты некоторые весьма значительные результаты. Однако поиск путей применения теории информации в других областях не сводится к тривиальному переносу терминов из одной области науки в другую. Этот поиск осуществляется в длительном процессе выдвижения новых гипотез и их экспериментальной проверки. Если, например, человек в определенной ситуации ведет себя подобно идеальному декодирующему устройству, то это является экспериментальным фактом, а не математическим выводом и, следовательно, требуется экспериментальная проверка такого поведения на широком фоне различных ситуаций.
Во-вторых, мы должны поддерживать образцовый порядок в своем собственном доме. На понятия теории информации очень большой, даже, может быть, слишком большой спрос. Поэтому мы сейчас должны обратить особое внимание на то, чтобы исследовательская работа в нашей области велась на самом высоком научном уровне, который только возможно обеспечить. Больше исследовать и меньше демонстрировать свои достижения, повысить требования к себе – вот что должно быть сейчас нашим лейтмотивом. Исследователям следует публиковать результаты только своих наиболее ценных работ и то лишь после серьезной критики как со своей стороны, так и со стороны своих коллег. Лучше иметь небольшое количество первоклассных статей, чем много слабо продуманных или недоработанных публикаций, которые не принесут чести их авторам и только отнимут время у читателей. Только последовательно придерживаясь строго научной линии, мы сможем достичь реальных успехов в теории связи и укрепить свои позиции.
___________________________
1) Shannon C., The Bandwagon, Trans. IRE, IT-2, № 1 (1956), 3.
Слово бандвагон (bandwagon) в Америке означает политическую партию, добившуюся популярности и победившую на выборах, или просто группу лиц, программа которых находит широкую поддержку населения. Слово состоит из двух частей: “band” (оркестр, джаз) и “wagon” (повозка, карета) и, возможно, связано с существовавшим обычаем, по которому победивший на выборах кандидат проезжал по городу в открытой машине с джазом. Но, кроме того, слово “band” применяется в теории связи, где оно означает полосу пропускания частот, так что в этом заглавии есть некоторая игра слов. – Прим. перев.
ЛИТЕРАТУРА
[1]. Кибернетика, или управление и связь в животном и машине. – 2-е издание. М.: Наука; Главная редакция изданий для зарубежных стран, 19с.
[2]. C. E. Shannon, «Communication in the presence of noise», Proc. Institute of Radio Engineers, vol. 37, no.1, pp. 10—21, Jan. 1949.
[3]. Колмогоров подхода к определению понятия «Количество информации» Новое в жизни, науке, технике. Сер. «Математика, кибернетика», N1, 1991, С.24-29. (Перепечатка из "Проблемы передачи информации", N1, 1965, С.1-7.)









 Мама мыла раму
Мама мыла раму