Элементы проективной геометрии (стр. 3 )

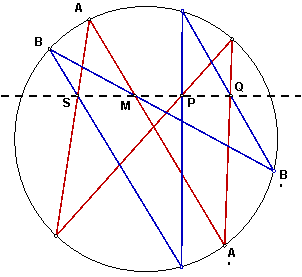
Поскольку мы рассматривем отображение, не являющееся перспективным, то прямая l является образом прямой m из пучка a, а ее образ – это прямая n из пучка b. (Для окружности прямые m и n были касательными в вершинах пучков, они же будут касательными и к конике.) Выберем еще в пучке a любую прямую а, а в пучке b – ее образ b. Точку пересечения прямых а и b назовем А. Проективное отображение полностью задается тремя парами соответственных элементов. В первом пучке возьмем прямые m, a, l, а в другом – их образы l, b, n.

Проведем через прямую n любую плоскость и построим в ней окружность, которая касается прямой n в точке N. Проведем касательную m' к окружности, проходящую через точку пересечения прямых m и n. Точку касания обозначим М'. Через прямую a и точку М' проведем плоскость, пересекающую окружность в точках М' и А'. Точку S пересечения прямых АА' и ММ', лежащих в одной плоскости, сделаем центром проекции.

Рассмотрим проекцию плоскости окружности на исходную плоскость с центром S. Точки М', А', N переходят в точки М, А, N. В плоскости окружности можно рассмотреть проективное отображение пучка с вершиной М' на пучок с вершиной N. Точки пересечения соответственных пучков порождают окружность. Соответствующее отображение пучков задается соответствием троек прямых m', a', l' и l', b', n. Эти прямые являются прообразами прямых m, a, l и l, b, n при центральной проекции. Значит, соответственные лучи пучков, порождающих окружность, переходят при проекции в соответственные лучи пучков, порождающих конику. Что и требовалось доказать.

Теорема Паскаля

Из доказанной теоремы следует, что если взять два пучка прямых с вершинами на любом коническом сечении, и рассмотреть отображение одного пучка на другой, такое что соответственные прямые пересекаются в точках, лежащих на конике, то это отбражение будет проективным, то есть сложное отношение прямых будет сохраняться.

Можно сформулировать этот результат и по-другому:

Выберем на конике четыре неподвижные точки A, B, C, D и пятую подвижную точку М. Сложное отношение прямых МA, МB, МC, МD не зависит от выбора точки М.

Новое определение конического сечения ставит перед нами естественную задачу на построение. Возьмем два пучка с вершинами М и N. Чтобы задать проективное отображение, достаточно выбрать в каждом пучке тройку прямых: a1, b1, c1 – в первом пучке и a2, b2, c2 – во втором. Три точки пересечения соответствующих прямых А, В, С лежат на конике. Кроме того, коника должна проходить еще и через точки М и N.

Значит, взяв любые (!) пять точек общего положения М, N, А, В, С, можно построить единственную конику, проходящую через эти точки. Две из этих пяти точек будут вершинами пучков, и из каждой вершины проводим по три прямые через три оставшиеся точки. Таким образом проективное отображение одного пучка на другой становится полностью определенным. Вершинами пучков при этом можно выбирать любые две точки. Коника будет получаться та же самая. (почему?)

Таким образом, уже доказана очень сильная теорема.

Теорема

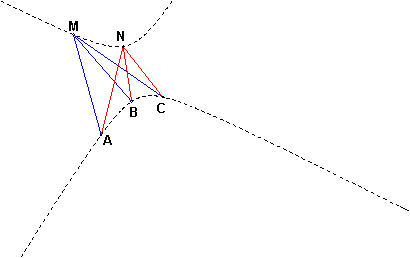
Фактически, имея пять исходных точек, мы можем постоить еще сколько угодно точек конического сечения. Действительно, взяв любую прямую из одного пучка, построим ее образ в другом пучке, тогда их точка пересечения будет лежать на искомой конике. Возвращаемся к уже известной задаче:

По данным четырем прямым a1, b1, c1, d1, проходящим через точку М, и трем прямым a2, b2, c2, проходящим через точку N, построить прямую d2 такую, чтобы выполнялось равенство (a1b1, c1d1) = (a2b2, c2d2).

Эта задача была полностью решена, когда мы давали определение проективного отображения пучков. Однако, решив ее другим способом, мы получим доказательство одной из самых замечательных теорем проективной геометрии – теорему Паскаля.

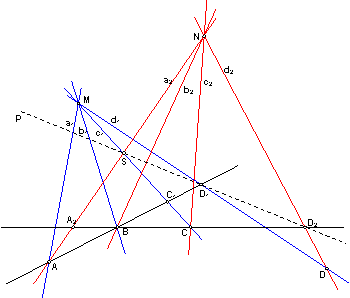
План построения будет следующим: сначала заменим сложное отношение прямых (a1b1, c1d1) сложным отношением точек, лежащих на одной прямой, потом спроецируем эти точки на другую прямую, и опять перейдем от точек к прямым a2, b2, c2, d2 с сохранением сложного отношения.

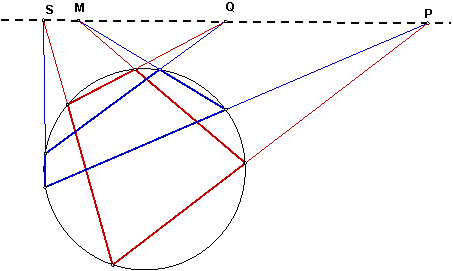
Пусть прямые a1, b1, c1, d1 пересекают прямую АВ в точках A, B, C1, D1. Тогда (a1b1, c1d1) = (AB, C1D1). Построим теперь центральную проекцию прямой АВ на прямую ВС. Центром проекции выберем точку S, в которой пересекаются прямые c1 и a2. Проекциями точек A, B, C1, D1 будут точки A2, B, C, D2. (AB, C1D1) = (A2B, CD2). Соединяя точки A2, B, C, D2 с точкой N, получаем три данные прямые a2, b2, c2 и четвертую прямую d2.

(a2b2, c2d2) = (A2B, CD2) = (AB, C1D1) = (a1b1, c1d1). Точка D пересечения прямых d1 и d2 лежит на конике.

Заметим, что в этом построении появляется всего одна прямая, которая не принадлежит двум исходным пучкам и не соединяет две исходные точки. Это прямая р, которая проходит через центр проекции S и соединяет точки D1 и D2.

Убирая с чертежа некоторые прямые и точки и вводя новые обозначения, получаем теорему Паскаля.

Теорема Паскаля

Пусть шесть точек АВCDMN лежат на произвольном коническом сечении, тогда точки пересечения прямых AN и CM, AB и DM, ВC и DN лежат на одной прямой.

Доказательство теоремы следует непосредственно из построения. Действительно, пять точек из шести данных полностью определяют конику. Проводя построение шестой точки, получаем прямую Паскаля. Это та самая прямая р, которая не проходит ни через одну из начальных пяти точек.

Паскаль доказал эту теорему, когда ему было всего 16 лет. Это случилось по крайней мере за 250 лет до того, как Штейнер сформулировал проективное определение коники. Нет сомнения, что доказательство Паскаля использовало только «классические» теоремы евклидовой геометрии.

Чтобы лучше разобраться с теоремой, рассмотрим щесть точек, лежащих на окружности. Соединяя их одну за другой, получим шестизвенную ломаную ABCMDN. Паскаль назвал ее «Hexagramma mysticum», мы назовем ее шестиугольником Паскаля.

Если эта ломаная ограничивает выпуклый шестиугольник, то пары отрезков AN и CM, AB и DM, ВC и DN являются его противоположными сторонами. В этом случае теорему Паскаля формулируют обычно так:

Точки пересечения противоположных сторон шестиугольника, вписанного в окружность (или коническое сечение), лежат на одной прямой.

Эту же формулировку можно оставить и для случая, когда ломаная не является выпуклой. «Противоположными сторонами шестиугольника» будем считать такие звенья ломаной, которые разделены ровно двумя другими звеньями с каждой стороны.

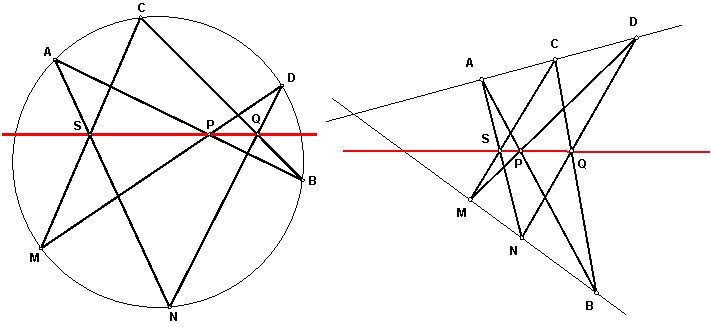
Здесь становится особенно хорошо видна связь между теоремой Паскаля и теоремой Паппа. В обеих теоремах речь идет о точках пересечения противоположных сторон шестиугольника. И в обеих теоремах эти точки лежат на одной прямой. И это, конечно же, не случайность.

Мы назвали коникой множество точек пересечения соответствующих прямых двух пучков, между которыми установлено проективное соответствие. Если эти пучки находятся в перспективном соответствии, то соответствующие прямые пересекаются на оси перспективы. Кроме того прямая, которая соединяет вершины пучков переходит сама в себя. Так что в этом случае под определение коники вполне подходят две пересекающиеся прямые.

Если давать определение конического сечения, как пересечения плоскости и конической поверхности, то рассмотрев плоскость, проходящую через вершину конуса, опять получим две пересекающиеся прямые. Естественно, поэтому, считать пересекающиеся прямые особым, «вырожденным» случаем коники. Теорема Паппа теперь становится частным случаем теоремы Паскаля.

Теорема Брианшона

Воспользуемся двойственностью точек и прямых на проективной плоскости, чтобы сформулировать теорему, двойственную теореме Паскаля. Брианшон сделал это почти через 150 лет после опубликования теоремы Паскаля. С тех пор во всех книгах по проективной геометрии эти две теоремы находятся рядом, иллюстрируя принцип двойственности.

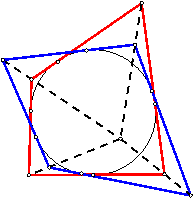
Возьмем шестиугольник Паскаля, вписанный в коническое сечение, и применим к нему полярное преобразование. Коника останется на месте, а вершины шестиугольника перейдут в свои поляры, то есть касательные к конике. Стороны шестиугольника перейдут в свои полюса, то есть точки пересечения шести поляр. Точки пересечения противоположных сторон вписанного шестиугольника превратятся в прямые, соединяющие вершины описанного шестиугольника. Поскольку три исходные точки лежали на одной прямой, три соответствующие поляры будут проходить через одну точку.

Теорема Брианшона

Прямые, соединяющие противоположные вершины шестиугольника, стороны которого касаются конического сечения, пересекаются в одной точке.

Интересно теперь поставить такой вопрос: что является образом коники при полярном преобразовании? Действительно, точки переходят в прямые, прямые – в точки, а во что перейдет коника?

Совершим сначала полярное преобразование коники относительно себя самой. Каждая точка коники перейдет в свою поляру – касательную к конике. Получается, что коника, которая была множеством точек, станет теперь множеством прямых. Это множество называют оболочкой коники.

Рассмотрим два пучка, порождающие конику. Между ними установлено проективное соответствие. В результате полярного преобразования прямые каждого пучка перейдут в точки одной прямой. Между точками двух прямых также будет установлено проективное соответствие, поскольку полярное преобразование сохраняет сложное отношение.

Точки пересечения соответственных прямых превратятся в прямые, соединяющие соответственные точки. Как мы только что выяснили, эти прямые являются касательными к конике. Значит оболочку коники можно представить, как множество прямых, соединяющих пары соответственных точек при проективном отображении одной прямой на другую.

Принцип двойственности позволяет высказать и более общее утверждение.

Рассмотрим две прямые, между точками которых установлено проективное соответствие. Множество прямых, соединяющих соответственные точки, образует оболочку какой-либо коники.

Полное доказательство этой теоремы приводить не будем. Вдумчивый читатель может рассмотреть оболочку коники, как центральную проекцию оболочки окружности и доказать двойственный аналог соответствующей теоремы о пучках.

Теперь можно сформулировать еще один замечательный двойственный результат.

А также:

Рассмотрим теперь проективное отображение прямой а на прямую а', при котором бесконечно удаленная точка одной прямой перейдет в бесконечно удаленную точку другой прямой. Поскольку прямые, соединяющие соответственные точки, являются касательными к коническому сечению, то среди этих касательных будет и бесконечно удаленная прямая. Коника, касающаяся бесконечно удаленной прямой, называется параболой. Прямые а и а' – касательные. Обозначим точки касания М и N.

Возьмем теперь еще какую-нибудь касательную к параболе, которая соединяет соответственные точки В и В'. Пусть прямые а и а' пересекаются в точке S. При отображении одной прямой на другую точка М переходит в S, точка S – в N, точка В – в В', бесконечно удаленная точка Х¥ – в бесконечно удаленную точку Х'¥.

Значит, (MS, BX¥) = (SN, B'Х'¥). Но . Следовательно, , то есть касательная к параболе делит отрезки двух других касательных в одном и том же отношении (в противоположных направлениях).

Отложим теперь на сторонах какого-либо угла два отрезка, начиная от вершины, и поделим каждый на n равных частей. Соединяя точки, которые делят отрезки в одном и том же отношении (см. чертеж), получаем семейство касательных к параболе.

Задача о бабочке

Мы уже неоднократно сталкивались с тем, что проективная геометрия служит источником разнообразных сложных задач по планиметрии. Вот еще одна знаменитая задача про окружность, известная как «задача о бабочке».

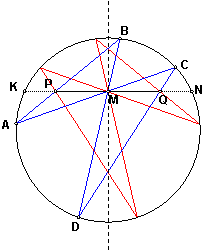
Пусть хорды окружности АС, BD и KN пересекаются в точке М, а прямая KN пересекает прямые АВ и CD и точках Р и Q. Если точка М является серединой хорды КМ, то MP = MQ.

Все известные «школьные» решения этой задачи довольно сложны. Дело в том, что в основе ее лежит проективная теорема, поэтому использовать в решении такие свойства окружности, как равенство радиусов или равенство вписанных углов, напрямую не получается. Приходится изобретать неочевидные дополнительные построения и всячески «выкручиваться». Если же перевести задачу на «проективный язык», решение становится вполне прозрачным.

Вместо окружности возьмем произвольную конику. Точка М пусть будет не серединой хорды, а произвольной точкой на некоторой прямой. На нашем чертеже эта прямая пересекает конику, хотя это совсем не обязательно. Выберем на прямой l еще одну точку Р и проведем через нее какую-нибудь прямую, пересекающую конику в точках А и В. Теперь проведем прямые АМ и ВМ до пересечения с коникой в точках С и D. Пусть прямая CD пересекает прямую l в точке Q.

Оказывается, положение точки Q на прямой l определяется только коникой и точками М и Р. «Бабочка» ABCD может быть любой (!), лишь бы сторона АВ проходила через точку Р, а прямые АС и BD пересекались в точке М.

Чтобы убедиться в этом построим полный четырехвершинник с вершинами A, B, C, D, который позволяет провести поляру m точки М. Пусть эта поляра пересекает прямую l в точке К. Положение точки К на прямой l зависит только от коники и точки М.

На стороне четырехвершинника АD образовалась гармоническая четверка АD, XY. Ее проекцией на прямую l является четверка КМ, PQ. Значит, точка Q – это четвертая гармоническая к точкам М, К, Р, положение которых не зависит от «бабочки» ABCD.

Другими словами:

Пусть четыре прямые пучка с вершиной М пересекают конику в точках АВ, CD, А'В', C'D', прямые АD и A'D' пересекаются в точке Р, прямые ВС и В'С' – в точке Q. Тогда точки Р, Q, М лежат на одной прямой.

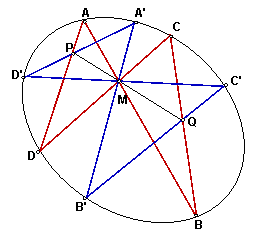
Это утверждение можно также вывести, используя теорему Паскаля. Возвратимся теперь к задаче о бабочке.

Проведем через точку М серединный перпендикуляр к отрезку KN и построим «бабочку», симметричную исходной. Точки Р и Q пересечения соответственных сторон двух «бабочек», во-первых, симметричны относительно проведенной оси, а во-вторых, лежат на одной прямой с точкой М. Отсюда сразу же получаем утверждение задачи.

Проективные отображения конических сечений

До сих пор мы рассматривали проективные отображения прямой на прямую и пучка на пучок. Попробуем рассмотреть отображение коники на конику или, что более важно, отображение коники самой на себя. Для этого надо лишь определить сложное отношение четырех точек коники или четырех касательных к конике.

Это определение естественным образом следует из ранее доказанных теорем. Возьмем на коническом сечении четыре произвольные точки A, B, C, D и пятую точку М. Как нам уже известно, сложное отношение прямых МA, МB, МC, МD не зависит от выбора точки М. Назовем это отношение сложным отношением четырех точек коники.

Точно так же, выбирая четыре касательные a, b, c, d и пятую касательную m, называем сложным отношением четырех касательных a, b, c, d сложное отношение точек их пересечения с прямой m. Это сложное отношение не зависит от выбора касательной m. Более того, сложное отношение четырех касательных равно сложному отношению точек касания. Это следует из того, что при полярном отображении точки коники переходят в ее касательные и наоборот, а все сложные отношения сохраняются.

В дальнейшем имеет смысл рассматривать невырожденную конику, как совокупность всех ее точек и, одновременно, всех ее касательных. Можно тогда без оговорок считать, что полярное преобразование конику переводит в конику. Точки и прямые при этом меняются местами.

Можно теперь рассмотреть отображение коники самой на себя, сохраняющее сложное отношение четырех точек (касательных). Если точки A, B, C, D переходят в точки A', B', C', D', то (AB, CD) = (A'B',C'D') (аналогично для касательных). Такое отображение назовем проективным. Оказывается, проективные отображения «хорошо устроены», то есть обладают многими полезными свойствами.

Покажем, во-первых, что проективное отображение коники на себя задается тремя точками и тремя их образами. Если известно, что точки A, B, C переходят в точки A', B', C', то образ D' любой другой точки D однозначно определен.

Заметим сначала, что поскольку сложное отношение четырех точек коники определено через сложное отношение четырех прямых, то для любых трех точек коники и заданного значения сложного отношения существует единственная точка, для которой это отношение принимает данное значение. Покажем теперь, как построить эту точку.

Рассмотрим два пучка с вершинами А и А'. Проведем прямую s через точки пересечения прямых АВ', А'В и АС', А'С. Построим перспективное отображение одного пучка на другой с осью перспективы s. Каждой прямой каждого пучка соответствует единственная точка коники. При этом точки А и А' соответствуют касательным в своих пучках. Отображение пучка на пучок задает отображение коники самой на себя. Сложное отношение, конечно же, сохраняется.

Значит образ D' точки D строится так:

Проводим прямую А'D до пересечения с осью s, затем соединяем получившуюся точку с точкой А и продолжаем до пересечения с коникой в точке D'.

Главное свойство проективного отображения коники на себя состоит в том, что положение оси перспективы s не зависит от выбора двух соответственных точек А и А'. Ось перспективы задается самим отображением.

Пусть задано проективное отображение коники на себя. Выберем любую пару точек А, В и их образов А', В'. Точки пересечения прямых АВ' и А'В лежат на одной прямой. Эта прямая s называется осью перспективы отображения коники на себя.

Для доказательства достаточно взять на конике три любые точки A, B, C и их образы A', B', C' и убедиться, что точки пересечения пар прямых АВ' и А'В, АС' и А'С, ВС' и В'С лежат на одной прямой. Это утверждение есть не что иное, как хорошо знакомая нам теорема Паскаля. Значит, для любого отображения коники задана его ось.

На нашем чертеже ось s не пересекает конику. Если же это не так, то точки пересечения коники с осью будут неподвижными точками отображения. (почему?) Кроме того, любое отображение можно задать парой соответственных точек А и А' и осью s.

Теорема Понселе

Свойства проективных отображений позволяют доказать теорему Понселе для треугольников. Сформулируем ее пока что следующим образом:

Если вершины двух трехвершинников принадлежат некоторой конике, то все их шесть сторон касаются другой коники.

Для доказательства рассмотрим два трехвершинника АВQ и CDP. Пусть стороны РС и PD пересекают прямую АВ в точках К и L, а стороны QA и QB пересекают прямую CD в точках M и N.

Сложное отношение четырех точек коники определяется через сложное отношение четырех прямых. Рассматривая пучок с центром в точке Р, получаем, что
(АС, DB) = (AK, LB). Точно так же рассматривая пучок с центром в точке Q, получаем, что (АС, DB) = (MС, DN). Следовательно, (AK, LB) = (MС, DN), и, значит, существует проективное отображение прямой АВ на прямую CD, при котором точки A, K, L, B переходят в точки M, С, D, N. Прямые, соединяющие соответственные точки отображения, принадлежат оболочке некоторой коники, что и требовалось доказать.

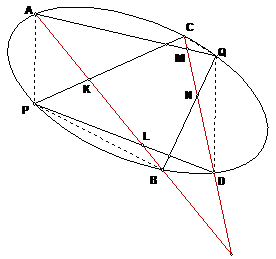Заметим, что любая коника полностью задается пятью своими касательными. Рассмотрим какой-либо трехсторонник, стороны которого касаются коники Γ1, а вершины лежат на конике Γ2. Если взять теперь любой трехсторонник с вершинами, лежащими на Γ2, и двумя сторонами, касающимися Γ1, то из доказанной теоремы следует, что и третья его сторона обязательно будет касаться той же самой коники Γ1.

Для двух окружностей теорему Понселе можно сформулировать так:

Пусть a и b – вписанная и описанная окружности одного и того же треугольника. Тогда для любой точки М, лежащей на окружности b, существует треугольник с вершиной М, вписанный в окружность b и описанный вокруг окружности a.

Центральное отображение

Важный случай проективного отображения коники на себя – центральное отображение. Строится оно следующим образом:

Возьмем любую точку S, не лежащую на конике и рассмотрим пучок с вершиной S. Если прямая пучка пересекает конику в точках А и А', то будем считать, что точки А и А' переходят друг в друга при центральном отображении с центром S. Если же прямая пучка касается коники в точке Р, то будем считать, что точка Р переходит сама в себя.

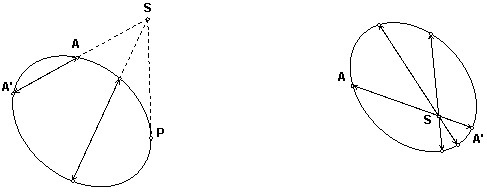
Докажем, что центральное отображение является проективным, а его ось – это поляра точки S.

Заметим сначала, что если прямые АА' и ВВ' пересекаются в полюсе S, то точки пересечения прямых АВ', А'В и АВ, А'В' лежат на поляре s.

Построим теперь отображение, заданное парой соответственных точек А, А' и осью s. Для любой точки В ее образ В' строится так:

Построим точку Р пересечения прямой А'В с осью s. потом проведем прямую АР до пересечения с коникой в точке В'. Нетрудно заметить, что поскольку ось s является полярой точки S, то прямая ВВ' проходит через полюс S. Более того, то же самое построение, будучи примененным к точке В', приведет обратно к точке В.

Значит, проективное отображение, заданное парой точек А, А' и осью s, совпадает с центральным отображением с центром S.

Точно так же несложно доказать, что если при проективном отображении коники хотя бы одна пара точек меняется местами, то отображение является центральным. Доказательство можно провести на том же самом чертеже.

Действительно, если точка А' является образом точки А, и одновременно, точка А является образом точки А', то построение точки В' по известной точке В можно вести двумя способами.

Можно строить прямую А'В, находить точку Р ее пересечения с осью, потом проводить прямую АР до пересечения с коникой в точке В'. Но можно идти и в обратном порядке. Построим точку Q пересечения прямой АВ с осью s. потом проведем прямую А'Q до пересечения с коникой в точке В'. Чтобы построение двумя способами привело к одной и той же точке В', прямая АА' должна обязательно проходить через полюс S оси s. Но в этом случае, как мы уже видели, отображение является центральным.

Используя доказанные свойства, решим интересную задачу.

Лемма

Композиция двух центральных отображений с центрами S и P является проективным отображением с осью SP.

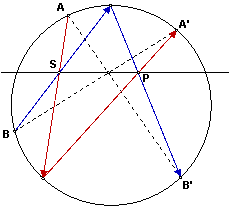Применим к точке А центральное отображение с центром S, а к ее образу центральное отображение с центром Р. Получим точку А'. Таким же образом из точки В получим точку В'. Точка пересечения прямых АВ' и А'В должна лежать на оси отображения. По теореме Паскаля все такие точки лежат на прямой SP. Значит она и будет осью отображения.

Теорема

Композиция трех центральных отображений, центры которых лежат на одной прямой, является центральным отображением с центром на той же прямой.

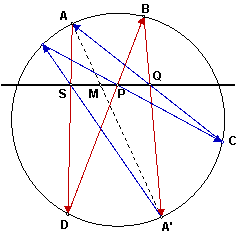Рассмотрим композицию трех центральных отображений с центрами S, P, Q. Применяя последовательно три отображения, построим образ точки А – точку А'.

Построим теперь образ точки А' при этой же композиции отображений. По теореме Паскаля мы вернемся обратно в точку А.

Значит, при композиции трех центральных отображений с центрами S, P, Q точки А и А' меняются местами. Следовательно это – центральное отображение. Назовем его центр М.

Последовательное применение всех четырех центральных отображений возвращает любую точку на ее исходное место или, как говорят, является тождественным отображением.

Значит, применяя к любой точке композицию отображений с центрами S и P, или же композицию отображений с центрами М и Q, (в обратном порядке!) будем получать один и тот же результат. Следовательно, осью этой композиции служит как прямая SP, так и прямая МQ. Это и значит, что точка М лежит на прямой, проходящей через точки S, P, Q.

Построим теперь все четыре центральные отображения для двух различных точек А и В. Получаем следующий результат:

Если в конику вписаны два четырехсторонника и точки пересечения трех соответственных сторон лежат на одной прямой, то и точка пересечения двух оставшихся сторон также лежит на этой прямой.

Интересно было бы найти «школьное» доказательство этой теоремы для двух четырехугольников, вписанных в окружность.

Можно, конечно же, сформулировать и двойственную теорему. Для этого построим полярное отображение. Вместо вписанных четырехсторонников появятся описанные четырехсторонники, а теорема станет звучать так:

Если вокруг коники описаны два четырехсторонника и прямые, соединяющие три соответствующие вершины, проходят через одну точку, то и прямая, соединяющая оставшиеся две вершины, также проходит через эту точку.

Рассматривая композицию трех произвольных центральных отображений коники на себя, получаем решение следующей задачи

Дана окружность (коника) и три произвольные точки, ей не принадлежащие. Построить треугольник (трехсторонник), вершины которого лежат на окружности (конике), а стороны проходят через данные точки.

Действительно, задача сводится к тому, чтобы найти неподвижную точку отображения, которое является композицией трех центральных отображений. Для этого достаточно построить образы трех произвольных точек А, В и С при этом отображении, и по трем точкам и их образам А', В' и С' построить ось отображения. Точки пересечения этой оси с коникой и будут неподвижными точками. Каждая из неподвижных точек является вершиной одного из искомых трехсторонников.

К сожалению, чертеж к задаче получается весьма запутанным и перегруженным вспомогательными линиями, так что нет смысла приводить его здесь. Гораздо полезнее построить его самостоятельно.

Произвольное отображение коники на себя

В самом начале мы рассматривали проективные отображения прямой на прямую. Но две прямые представляют собой вырожденный случай конического сечения. В таком случае, отображение одной прямой на другую есть частный случай отображения коники на себя, а центральная проекция одной прямой на другую соответствует центральному отображению коники.

Рассмотрим отображение одной прямой на другую, не являющееся центральной проекцией. Как известно, прямые, соединяющие соответственные точки, образуют линейную оболочку некоторой коники. Оказывается, это утверждение оказывается верным и для невырожденной коники.

Теорема

Рассмотрим произвольное нецентральное проективное отображение коники на себя. Прямые, соединяющие соответствующие точки отображения, образуют линейную оболочку некоторой коники.

Чтобы доказать эту теорему, сведем случай произвольной коники к двум пересекающимся прямым. Выберем две произвольные прямые MM' и NN', соединяющие соответственные точки и покажем, что отображение коники на себя порождает отображение этих прямых друг на друга.

Заметим сначала, что прямые АВ' и А'В пересекаются в точке В0, лежащей на оси отображения s. Следовательно, точка В1, в которой пересекаются прямые АА' и ВВ', лежит на поляре точки В0.

Возьмем теперь произвольные точки М, А, В, С, D, и их четыре образа М' А', В', С', D'. По определению проективного отображения (AB, CD) = (A'B',C'D'). Теперь рассмотрим точки А1, В1, С1, D1 пересечения прямых АА', ВВ', СС' DD' с прямой ММ'.

Эти точки лежат на полярах точек А0, В0, С0, D0. Все эти поляры проходят через точку S, полюс оси s. При этом сложное отношение четырех поляр равно отношению полюсов (А0В0,С0D0).

Значит, (А0В0,С0D0) = (А1В1,С1D1), но по определению сложного отношения четырех точек коники, равному отношению четырех прямых, проходящих через точку М', (А0В0,С0D0) = (AB, CD). Значит, (А1В1,С1D1) = (AB, CD), и это равенство не зависит от выбора точек М и М'.

Выберем теперь две прямые ММ' и NN'. Получается, что для любой четверки прямых АА', ВВ', СС' DD' сложное отношение точек их пересечения с прямыми ММ' и NN' будет одним и тем же. Значит, отображение коники на себя порождает отображение прямой ММ' на прямую NN', откуда и следует утверждение теоремы.

Произвольное отображение коники на себя (продолжение)

Получается, что проективное отображение коники на себя порождает другую конику. Попробуем разобраться, как эти две коники связаны между собой. Если отображение имеет неподвижные точки, то дело обстоит достаточно просто. Касательная в неподвижной точке исходной коники является прямой, соединяющей соответственные точки отображения. Здесь мы считаем, что касательная «соединяет точку А с точкой А». Значит, эти касательные входят в линейную оболочку порожденной коники.

Получается, что порожденная коника касается исходной в двух неподвижных точках. Но если неподвижных точек нет, то коники вообще не имеют общих точек. Можно конечно сказать, что коники касаются в двух мнимых точках, но, к сожалению, предъявить эти точки на чертеже нельзя. Мнимые точки появляются внутри довольно сложной и абстрактной алгебраической модели. Область математики, исследующая свойства этих моделей, называется геометрией (землемерием) только в силу исторической традиции. Уравнениям, описывающим различные «геометрические» объекты давно уже не соответствуют никакие чертежи.

Если же мы хотим остаться в рамках «синтетической» геометрии (с чертежами), то придется сформулировать такое свойство взаимного расположения этих двух коник, которое не зависит от наличия точек пересечения.

Заметим сначала, что прямая s, соединяющая неподвижные точки отображения – это его ось. Очевидно, полюсом этой прямой относительно обеих(!) коник является точка пересечения общих касательных. Можно ожидать, что и в случае отсутствия общих точек ось отображения будет иметь один и тот же полюс относительно двух коник. И это действительно так.

Для доказательства заметим, что полюс и поляру связывают два взаимно двойственных построения. Поляра по известному полюсу строится с помощью вписанного четырехвершинника, полюс по известной поляре – с помощью описанного четырехсторонника. Идея доказательства – совместить эти два построения.

Одно построение применим к исходной конике, заданной как множество точек, а второе – к порожденной конике, получившейся как линейная оболочка, то есть множество прямых. Покажем, что в результате для оси отображения получится один и тот же полюс.

Рассмотрим полюс S оси отображения относительно исходной коники. Нетрудно убедиться, что если выбрать на конике две точки А и В таких, что прямая АВ проходит через полюс S, и построить их образы А' и В', то прямая А'В' также будет проходить через этот полюс.

Действительно, прямые А'В и АВ' пересекаются на оси s. Поляра точки пересечения М проходит как через полюс S, так и через точку пересечения диагоналей АВ и А'В'. Но полюс уже лежит на прямой АВ, откуда и следует справедливость утверждения. Кроме того получаем, что и точка N пересечения АА' и ВВ' также лежит на оси s.

Прямые АА' и ВВ' входят в линейную оболочку порожденной коники, то есть являются касательными к ней. Построим теперь еще две касательных. Для этого применим отображение к точкам А' и В' и получим точки А'' и В''. Прямая А''В'' также проходит через полюс S, а прямые А'А'' и В'В'' касаются порожденной коники. При этом точка пересечения прямых А'А'' и В'В'' опять же лежит на оси s.

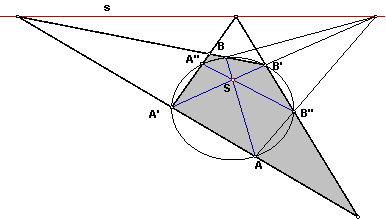Рассмотрим теперь четырехсторонник, образованный прямыми АА', ВВ', А'А'', В'В''. Его стороны касаются порожденной коники, а точки пересечения противоположных сторон лежат на оси s. Значит, его диагонали проходят через полюс прямой s относительно порожденной коники. Но одна из его диагоналей – прямая А'В'.

Значит, если прямая АВ проходит через полюс исходной коники, то прямая А'В' проходит через полюс порожденной коники. Применим это же утверждение к прямой А'В'. Поскольку она проходит через полюс исходной коники, то прямая А''В'' проходит через полюс порожденной коники. Значит полюс порожденной коники совпадает с точкой пересечения прямых А'В' и А''В'', то есть с точкой S. Что и требовалось доказать.

Верно и более сильное утверждение. Чтобы его сформулировать заметим, что любая коника порождает для любой прямой, не являющейся касательной, проективное отображение этой прямой на себя. Строится оно следующим образом:

Возьмем на прямой s произвольную точку А и построим ее поляру а. Точку А' пересечения поляры а с прямой s будем считать образом точки А.

Это отображение действительно является проективным, поскольку сложное отношение четырех точек прямой равно сложному отношению четырех их поляр.

Кроме того, в силу принципа двойственности, если поляра точки А проходит через точку А', то и поляра точки А' проходит через точку А. Трехвершинник SАА' – автополярный. Значит, при данном отображении точка А' переходит обратно в точку А. Отображения, при которых точки обмениваются местами, называют инволюциями. Поэтому, отображение, которая коника порождает на прямой, называют инволюцией сопряженных точек.

Если прямая s пересекает конику, то инволюция меняет местами точки в парах, которые гармонически разделяют точки пересечения. Сами точки пересечения остаются на месте. Если же коника и прямая s не пересекаются, то инволюция не имеет неподвижных точек.

Возвращаясь к двум касающимся коникам – исходной и порожденной, сформулируем следующее утверждение:

Обе коники порождают на оси отображения одну и ту же инволюцию сопряженных точек.

Утверждение является вполне очевидным, если ось отображения пересекает исходную конику. Действительно, в этом случае инволюция однозначно задается двумя неподвижными точками. Для любой точки А прямой s ее образ строится, как четвертая гармоническая точка к ней самой и двум неподвижным точкам.

Если же коника и ось отображения не пересекаются, то придется доказать, что любая точка, лежащая на оси, имеет одну и ту же поляру относительно обеих коник.

Заметим сначала, что если стороны четырехвершинника касаются коники, то его диагонали образуют автополярный трехвершинник, то есть каждая диагональ является полярой противоположной вершины. Применим это утверждение к двум коникам.

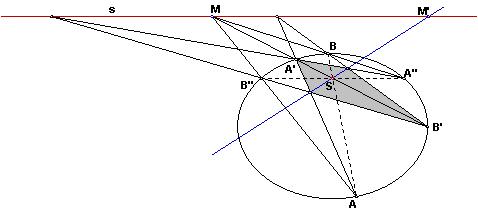Возьмем на оси отображения любую точку М и проведем прямую MS, точки ее пересечения с коникой обозначим А' и В'. Построим теперь точки А, В, А'', В'' (обозначения предыдущей теоремы). Получаем, что диагональ четырехсторонника, описанного вокруг порожденной коники, является полярой точки М. Та же диагональ SM' будет полярой точки М и относительно исходной коники. Это следует из того, что она проходит через точки пересечения прямых АА' и В'В'', ВВ' и А'А'', каждая из которых лежит на поляре.

Из того, что прямая SM' является полярой точки М относительно обеих коник следует, что обе коники порождают на оси s одну и ту же инволюцию сопряженных точек.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3