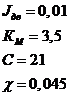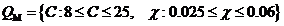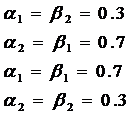Задание №9
Тема «Метод расчета мехатронной системы привода радиотелескопа на основе равновесно-арбитражной балансировки»
Общее описание задачи расчета мехатронной системы.
В настоящее время вопросы проектирования, модификации и управления в технических системах в соответствии с основными результатами относительно нового научно-технического направления – мехатроники – базируются на универсальной структуре мехатронной системы в виде трех, в общем случае, равнозначных сильно связанных подсистем: механической (конструкция), электротехнической (привод) и компьютерной подсистемы управления.
К подобным системам могут быть отнесены: летательные аппараты, робототехнические системы, следящие приводы радиотелескопов, а также множество других систем.
В процессе проектирования и модификации управляемых мехатронных систем формулируются векторные требования к каждой подсистеме в виде показателей эффективности и потерь, типы и допустимые множества изменяемых параметров и управляющих сил, варьируемые схемы и модели подсистем.
В большинстве случаев разработчики подобных систем идут по пути последовательного создания и оптимизации каждой из подсистем. Например, в начале создается механическая часть, затем под нее разрабатывается электротехническая часть и, наконец, выбираются алгоритмы и носители алгоритмов управления.
В данном докладе обсуждается подход к проблеме оптимизации мехатронной системы как многообъектной многокритериальной системы (ММС) на основе стабильно-эффективных игровых компромиссов, позволяющий одновременно учесть требования к каждой из подсистем в условиях исходной структурной несогласованности и к системе в целом и найти компромиссную комбинацию параметров. При этом работа системы оценивается показателями качества, которые позволяют оптимизировать не только каждую подсистему, но и всю мехатронную систему в целом. В исследовании применяются методы оптимизации ММС в условиях исходной структурной несогласованности, конфликта и неопределенности.[1]
Математическая модель привода, управляющие параметры, показатели. Постановка задачи.
В качестве математической модели ММС выбирается система, описывающая процесс взаимодействия 3 подсистем привода радиотелескопа показанных рис 1.
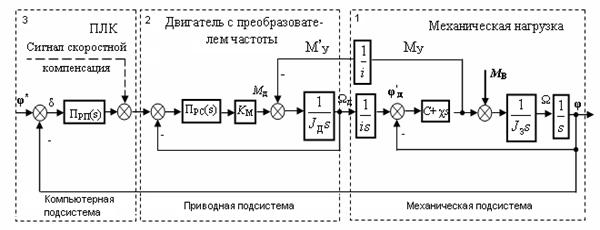 Рис. 1.1. Структурная схема мехатронной модели привода радиотелескопа
Рис. 1.1. Структурная схема мехатронной модели привода радиотелескопа
Передаточная функция ПИД-регулятора скорости имеет следующий вид:
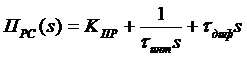 .
.
Здесь ![]() ,
, ![]() ,
, ![]() – настраиваемые параметры регулятора скорости.
– настраиваемые параметры регулятора скорости.
Выражения для расчета параметров ПИД-регулятора будут следующими[2]:
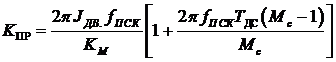
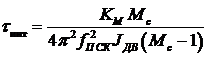
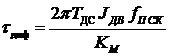
Фильтр в цепи сигнала обратной связи по скоростной подсистеме имеет передаточную функцию:
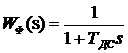
Передаточная функция ПИД-регулятора компьютерной подсистемы имеет следующий вид:
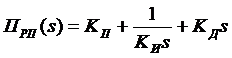 .
.
Расчётные формулы для определения параметров регулятора компьютерной подсистемы [2]:
![]()
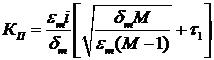
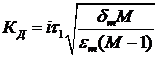
τ1 = (0,1-0,05)ТФ = (0,1-0,05)ТЗ
ТФ= ТЗ, τФ = τ
Сигнал постоянной компенсации представляет собой антирезонансный фильтр с передаточной функцией 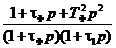
Передаточная функция механической подсистемы имеет вид:
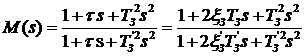
Постоянные времени:

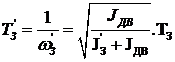
коэффициенты затухания:
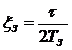
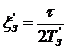
![]()
Управляющие силы. В математической модели вводятся управляющие силы для компьютерной и приводной подсистем и для механической подсистемы в виде векторов параметров 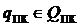 и
и ![]() соответственно.
соответственно.
При этом вектор параметров:
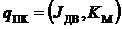 ,
,
где ![]() - момент инерции ротора двигателя,
- момент инерции ротора двигателя, ![]() - коэффициент пропорциональности между электромагнитным моментом и сигналом задания тока.
- коэффициент пропорциональности между электромагнитным моментом и сигналом задания тока.
Множество ![]() имеет вид:
имеет вид:
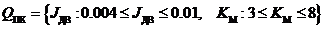 ,
,
Неравенства (2) характеризуют допустимый разброс свойств разных типов двигателей, которые могут быть использованы в приводе угла места радиотелескопа.
Аналогично, вектор «управляющих» параметров для механической подсистемы:
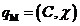 ,
,
где ![]() - коэффициент жёсткости механической передачи,
- коэффициент жёсткости механической передачи, ![]() - коэффициент диссипативных потерь в механической передаче.
- коэффициент диссипативных потерь в механической передаче.
Множество ![]() имеет вид:
имеет вид:
Векторный целевой показатель. Введенный векторный целевой показатель формирует многокритериальное целевое качество управления в условиях структурной несогласованности неопределенности, т. е. позволяет учесть некоторые технические требования при упругих колебаниях зеркала и типичные «целевые» свойства при взаимодействии подсистем привода.
Векторный показатель в рассматриваемой ситуации задан в виде двух показателей для каждого объекта:
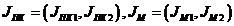
Показатели механической подсистемы и критерии оптимизации имеют следующий вид:
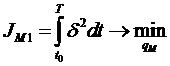
- ошибка слежения в контуре позиционного управления привода угла места радиотелескопа на интервале времени (![]() ).
).
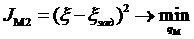
- допустимый коэффициент затухания собственных упругих колебаний зеркала радиотелескопа (где ![]() - заданная допустимая величина коэффициента собственных упругих колебаний зеркала).
- заданная допустимая величина коэффициента собственных упругих колебаний зеркала).
Показатели скоростной подсистемы и подсистемы контура положения и критерии оптимизации имеют следующий вид:
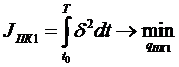
- ошибка слежения в контуре позиционного управления привода угла места радиотелескопа на интервале времени (![]() ).
).
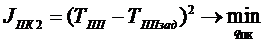
- показатель качества работы подсистем в виде времени переходного процесса (где ![]() - заданная допустимая величина времени переходного процесса).
- заданная допустимая величина времени переходного процесса).
Нормированные векторные показатели скаляризуются в виде:
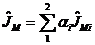 ,
, 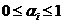 ,
,![]()
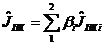 ,
,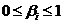 ,
, ![]()
где ![]() – нормированные весовые коэффициенты степени значимости показателя в сумме.
– нормированные весовые коэффициенты степени значимости показателя в сумме.
Анализ основных принципов оптимальности, форм компромиссов и методов решения на основе понятий стабильности и эффективности
В соответствии с понятиями стабильности и эффективности многие из существующих принципов оптимальности связаны с тремя базовыми: оптимальность на основе гарантированных подходов, коалиционного равновесия и кооперативных соглашений.
Принцип оптимальности на основе гарантированных решений базируется на исследовании максиминных и минимаксных задач и равновесных (седловых) решений.
Принцип оптимальности на основе коалиционного равновесия связан с игровыми подходами в виде скалярного Нэш-равновесия, векторных равновесий (в частности, «сильного» равновесия, векторного Нэш-равновесия, ![]() -равновесия и др.), коалиционного равновесия на основе V-решений («угроз и контругроз») и др.
-равновесия и др.), коалиционного равновесия на основе V-решений («угроз и контругроз») и др.
Принцип оптимальности на основе кооперативных соглашений содержит два основных взаимосвязанных направления: векторная оптимизация для определения множества Парето-решений (без структурных свойств ММС) (скаляризация, лексикографическая оптимизация, пороговая оптимизация и принцип сложности, оптимизация на основе конусов доминирования, среднеквадратическая оптимизация и др.) и исследование кооперативной игры в форме характеристической функции (с элементами учета структуры ММС: коллективной и индивидуальной рациональности и т. д.) Причем решаются задачи получения множества Парето и выбора кооперативного (эффективного) компромисса.
Известны также определенные результаты по комбинированию стабильных и эффективных решений (некоторые условия их совпадения, методы доминирования, некоторые методы комбинирования Парето-решений, максиминных решений, Нэш-решений, предостережений типа «угроз-контругроз», работы по анализу условий вступления в коалицию и др.).
Можно выделить ряд свойств задач управления ММС, которые свидетельствуют о необходимости формирования компромиссов и создают определенную основу для этого:
· наличие в целевой эффективности ММС индивидуальных и общих интересов;
· изменение информационных условий в ММС (неполнота информации и информационное «перемирие» с добровольным обменом (при наличии искажений – «блефа») и «добыванием» информации, связь субъективной и объективной информационных ситуаций);
· возможности и условия образования коалиций и различных коалиционных структур в ММС для повышения индивидуальной и общей эффективности в ММС на основе предостережения (наказания и поощрения);
· комбинации стабильных и эффективных решений на основе необязательных соглашений или обязательной договорной основе (например, выбор наиболее эффективного стабильного решения, стабильного среди эффективных и др.);
· стремление ММС к предельному целевому качеству с обеспечением минимальной межуровневой конфликтности (между «арбитром» и «линейкой» равнозначных объектов – коалиций ММС) на основе обобщенного гомеостаза и т. д.
Основные определения эффективности и стабильности. Методы и алгоритмы стабильно-эффективного управления
Целью данной работы является изучение методов и алгоритмов стабильного и эффективного управления, способов формирования стабильно-эффективных компромиссов ММС (СТЭК ММС) с последующим применением средств автоматизированного проектирования и реализацией методов в прикладных задачах.
Определения стабильности и эффективности, используемые в работе, без ограничения общности, сформулируем в рамках параметризованных управлений и/или процедур принятия решения, причем на общий вектор параметров ![]() наложены ограничения
наложены ограничения ![]() , где
, где
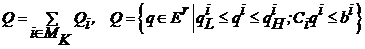 ,
,
где 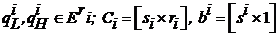 .
.
Понятия эффективного управления базируется на Парето-оптимальном решении, ![]() -оптимальном решении и дележе Шепли.
-оптимальном решении и дележе Шепли.
Определение 1.1. Пусть множество индексов коалиции ![]()
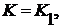
![]() . Вектор
. Вектор 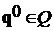 оптимален по Парето, если из условия
оптимален по Парето, если из условия 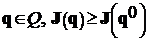 следует либо
следует либо ![]() , либо система неравенств несовместна и хотя бы одно из неравенств противоположного смысла.
, либо система неравенств несовместна и хотя бы одно из неравенств противоположного смысла.
Определение 1.2. Пусть ![]() – многогранный конус, определенный матрицей
– многогранный конус, определенный матрицей 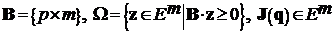 .
.
Пусть 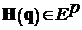 – новый векторный показатель вида
– новый векторный показатель вида 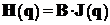 . Тогда оптимальное по Парето множество для
. Тогда оптимальное по Парето множество для ![]() совпадает с
совпадает с ![]() -оптимальным множеством для
-оптимальным множеством для ![]() .
.
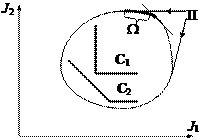
Рис. 1.2 Парето - и ![]() -оптимальность
-оптимальность
На рис. 1.2 для ![]() приведены два конуса
приведены два конуса 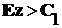 и
и ![]() .
.
Из рис. 1.2 видно, что прямоугольный конус типа конуса с вершиной в точке С1 удовлетворяет всей области П-Парето-решений, а «узкий» конус с вершиной С2 выделяет на Парето-области подобласть ![]() -оптимальных решений.
-оптимальных решений.
Определение 1.3. Набор параметров ![]() называется оптимальным по Шепли, если обеспечивает
называется оптимальным по Шепли, если обеспечивает 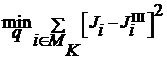 , где
, где 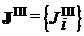 – функция Шепли, которая, например, при
– функция Шепли, которая, например, при 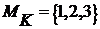 имеет вид
имеет вид
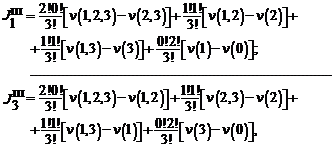
где 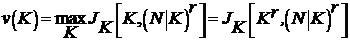 – характеристическая функция, как точка равновесия по Нэшу (см. определение 1.4). Например,
– характеристическая функция, как точка равновесия по Нэшу (см. определение 1.4). Например, ![]() означает:
означает: 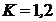 ,
, ![]() ,
, ![]() .
.
Стабильные решения формируются в виде гарантирующих решений, скалярного равновесия по Нэшу, векторных равновесий (векторное равновесие по Нэшу, ![]() -равновесие) и коалиционного равновесия на основе V-решений в форме угроз-контругроз (УКУ) Вайсборда–Жуковского.
-равновесие) и коалиционного равновесия на основе V-решений в форме угроз-контругроз (УКУ) Вайсборда–Жуковского.
Определение 1.4. Набор решений 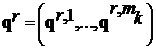 является равновесным по Нэшу относительно скалярного показателя
является равновесным по Нэшу относительно скалярного показателя 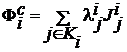 , который является функцией эффективности коалиции
, который является функцией эффективности коалиции ![]() , если для любого
, если для любого
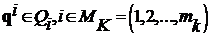 ,
, ![]() ,
,
где 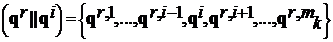 .
.
Определение 1.5. (частный случай определения 1.4).
Если 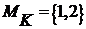 и цели антагонистические, т. е.
и цели антагонистические, т. е. 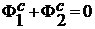 , то равновесие по Нэшу превращается в седловую точку
, то равновесие по Нэшу превращается в седловую точку
![]() .
.
Определение 1.6. Набор параметров ![]() называется гарантирующим решением для показателя
называется гарантирующим решением для показателя 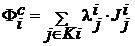 коалиции
коалиции ![]() , если
, если 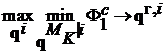 .
.
Определение 1.7. Набор векторов параметров 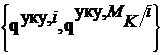 , где
, где 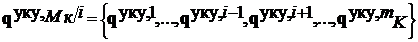 называется коалиционным равновесием (V-решением в форме угроз-контругроз (УКУ)) при показателе коалиции
называется коалиционным равновесием (V-решением в форме угроз-контругроз (УКУ)) при показателе коалиции 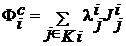 , если при попытке коалиции
, если при попытке коалиции ![]() улучшить свой показатель (угроза –
улучшить свой показатель (угроза – ![]() )
)
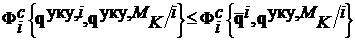
на множестве P допустимых коалиционных структур существует возможность создания контркоалиции 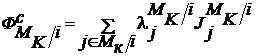 , для которой реализуется контругроза
, для которой реализуется контругроза ![]()
![]() ;
;
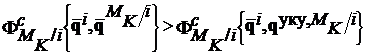 .
.![]()
Определение 1.8. Набор параметров ![]() является равновесным по Нэш относительно векторного показателя
является равновесным по Нэш относительно векторного показателя ![]() , где
, где 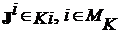 (фиксированная коалиционная структура), если набор
(фиксированная коалиционная структура), если набор ![]() является V-решением без угроз и если для любых
является V-решением без угроз и если для любых ![]() и
и ![]() из условия
из условия 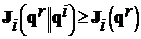 следует лишь
следует лишь ![]() (т. е. на векторе
(т. е. на векторе ![]() имеет место Парето-оптимальность).
имеет место Парето-оптимальность).
Определение 1.9. Набор векторов параметров ![]() называется W-равновесным относительно векторного показателя
называется W-равновесным относительно векторного показателя ![]() , где
, где 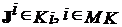 , если
, если ![]() есть V-решение без угроз и если для любых
есть V-решение без угроз и если для любых ![]() и
и 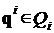 из условия
из условия ![]() , где
, где 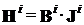 , следует либо
, следует либо ![]() , либо его несовместность (т. е. на векторе в соответствии с определением 1.2 имеет место W-оптимальность).
, либо его несовместность (т. е. на векторе в соответствии с определением 1.2 имеет место W-оптимальность).
Определения стабильных и эффективных решений позволили далее описать методы поиска этих решений на основе математического и алгоритмического обеспечения.
Классификация стабильно-эффективных компромиссов (СТЭК) ММС на основе необязательных соглашений Мулена и строгой договорной основе.

Смысл компромиссов на основе комбинации Парето–Нэш–УКУ–Шепли-подходов.
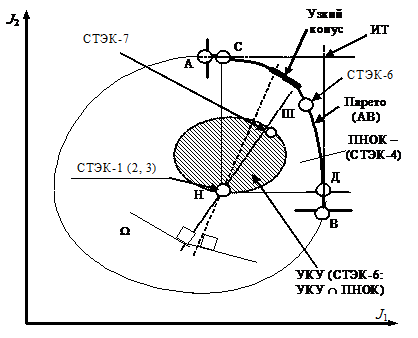
П – Парето-граница АВ; Н – Нэш-равновесие; УКУ – область угроз-контругроз;
ИТ – идеальная точка; УК – W-оптимальная часть П-границы на основе узкого конуса W;
Ш – точка Шепли; СНД – Парето–Нэш-область компромиссов (ПНОК)
СТЭКи заключаются в выборе недоминируемого наиболее эффективного Нэш-решения (точка Н), формировании Парето–Нэш-области компромиссов (ПНОК) на основе прямоугольного конуса СНД, границей которой является Парето-граница. В области ПНОК выбираются УКУ-решения в той или иной степени близости к точке Шепли либо к «идеальной» точке. Результирующим на основе остальных является СТЭК-7. Участникам игры имеет смысл выполнять необязательные соглашения в связи с устойчивостью ситуации в точке УКУ-решения.
В рамках обязательных соглашений рассматриваются комбинации арбитражных схем с УКУ–Нэш-равновесием, среднеквадратических решений с точкой Шепли и др.
Игровые подходы имеют большую значимость в развитии интеллектуальных систем управления (ИСУ, в состав которых входят, по меньшей мере, два присущих лишь ИСУ блока: динамическая экспертная система (ДЭС) и подсистема предельного целевого качества (ППЦК). Кроме необходимости пополнения базы знаний ДЭС разрабатываемыми игровыми алгоритмами, с одной стороны, и интеллектуализации компромиссов с учетом возможностей ИСУ, с другой стороны, в настоящее время разрабатывается концепция формирования ППЦК на основе игровых компромиссов в ММС и обобщенного гомеостаза, а также на основе игровых компромиссов в иерархических системах.
СТЭК НА ОСНОВЕ ПАРЕТО-НЭШ-ШЕПЛИ-КОМБИНАЦИЙ И АКТИВНЫХ РАВНОВЕСИЙ.
В данном разделе рассматриваются схемы формирования компромиссов, их систематизация на основе принципа необязательных соглашений и в условиях, в основном, объективной информации о ММС.
Технология формирования компромиссов базируется на интерактивных процессах, комбинирующих указанные модули оптимизаций с разной степенью автоматизации интерактивных процедур.
Интерактивные процедуры, как и модули оптимизации, реализуются, в основном, в программной системе многокритериальной оптимизации многообъектных динамических систем («МОМДИС»), описание которой дано в пункте 3 данного учебного пособия.
Результат оптимизации, как и ранее, позволяет получить параметры программно-корректируемых законов управления (ПКЗУ), оптимальные управления и решения в ММС.
Параллельная реализация модулей оптимизации позволяет обеспечить реальное время для схем СТЭК.
Большинство схем СТЭК полностью реализованы в среде «МОМДИС», «MATLAB», «DELPHI» или в собственной среде, некоторые схемы СТЭК имеют заявочный характер.
Далее формируется математическое описание схем СТЭК и общие блок-схемы предлагаемых интерактивных алгоритмов.
Выбор наиболее эффективного решения по Нэшу (СТЭК-1).
Потребность в данном СТЭК возникает, когда скалярное равновесие по Нэшу при фиксированной структуре ММС является неединственным. Практически речь идет о выборе недоминируемых решений по Нэшу.
Определение 2.1. Нэш-решение игры Г(Р)
![]() , где Ki ÎP = МK, i = 1,...,l; uÎU
, где Ki ÎP = МK, i = 1,...,l; uÎU
доминирует решение ![]() , если
, если
JKi(![]() ) ³ JKi(
) ³ JKi(![]() ), i = 1,…,l.
), i = 1,…,l.
В рамках СТЭК-1 предполагается, что недоминируемое решение ![]() – единственное, тогда оно наиболее эффективно для всего коалиционного разбиения ММС, поэтому принимается игроками как необязательное соглашение.
– единственное, тогда оно наиболее эффективно для всего коалиционного разбиения ММС, поэтому принимается игроками как необязательное соглашение.
Алгоритмическая схема СТЭК-1 может быть сформирована с помощью одного из методов Парето-оптимизации на конечном множестве точек. Одной из технологически удобных процедур является Парето-оптимизация на основе конусов доминирования.
Условие доминирования решения ![]() над
над ![]() относительно конуса W с матрицей В имеет простой вид
относительно конуса W с матрицей В имеет простой вид
BDJ ³ 0, (2.1)
где DJ = ![]() –
–![]() ,
,![]() = J(
= J(![]() ),
),![]() = J(
= J(![]() ).
).
Знак неравенства меняется, если эффективность ‑ минимизация потерь.
Как известно, при В = Е многогранный конус W становится прямоугольным, а процедура оптимизации на основе конуса W сводится к Парето-оптимизации.
В терминах рассмотренной ранее реализации данного метода конечное множество значений вектора J задаёт таблицу испытаний, по которой происходит попарное сравнение точек таблицы и выделение недоминируемой. При этом на каждой итерации исключаются точки ![]() , обеспечивающие обратный знак соотношения (2.1), таким образом, итерация алгоритма для получения СТЭК-1 состоит из трёх этапов.
, обеспечивающие обратный знак соотношения (2.1), таким образом, итерация алгоритма для получения СТЭК-1 состоит из трёх этапов.
Этап 1. Получение решения, равновесного по Нэшу.
Этап 2. Сравнение данного решения с ранее полученными на основе (2.1).
Этап 3. Исключение доминируемых решений на данном подмножестве.
Данная схема реализуется на интерактивной комбинации программных модулей ПС «MOMДИС».
Выбор компромиссного недоминируемого Нэш-решения по критерию уравновешивания потерь в окрестности наилучшего для каждой коалиции Нэш-решения (СТЭК-2).
Предыдущий СТЭК-1 может иметь неединственное недоминируемое решение uri, i = 1,2,...,n. Тогда сужение полученного множества может быть достигнуто дополнительными компромиссными условиями близости к наилучшему (идеальному) для каждой коалиции значению показателя ![]() и/или уравновешиванию потерь
и/или уравновешиванию потерь ![]() в связи с его недостижимостью, где
в связи с его недостижимостью, где
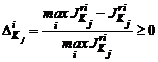 . (2.2)
. (2.2)
По данным двум условиям может быть введён дополнительный критерий оптимизации на конечном множестве недоминируемых Нэш-решений
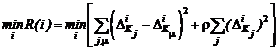 , (2.3)
, (2.3)
где j, m = 1,...,l; j ¹ m.
В (2.3) первая сумма обеспечивает уравновешивание потерь, вторая – близость к идеальной, на основе Нэш-решений, точке, а множитель r(1 ³ r ³ 0) определяет влияние степени близости на компромисс.
В частном случае, при l = 3 и r = 0 критерий принимает следующий простой вид:
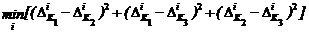 .
.
При достаточно ограниченном числе недоминируемых Нэш-решений после вычисления наборов![]() остаётся осуществить прямой перебор на конечном множестве для получения компромиссного решения
остаётся осуществить прямой перебор на конечном множестве для получения компромиссного решения ![]() .
.
Поэтому общая схема метода для получения СТЭК-2 имеет следующую общую этапную структуру.
Этап 1. Получение решения, равновесного по Нэшу.
Этап 2. Сравнение данного решения с ранее полученными на основе соотношения (2.1).
Этап 3. Исключение доминируемого решения и переход к этапу 1.
Этап 4. Нахождение полного набора недоминируемых решений и переход к этапу 5.
Этап 5. Получение точек 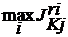 и переход к этапу 6.
и переход к этапу 6.
Этап 6. Вычисление разностей ![]() ,
, 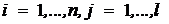 и переход к этапу 7.
и переход к этапу 7.
Этап 7. Формирование процедуры перебора недоминируемых Нэш-решений по критерию (2.3) при фиксированном r.
Интерактивные процедуры Нэш-оптимизации и оптимизации таблицы испытаний Нэш-решений дополняются процедурами вычисления наибольших значений ![]() , наборов
, наборов ![]() и функции R(i), которая позволяет выбрать компромиссное недоминируемое решение равновесное по Нэшу.
и функции R(i), которая позволяет выбрать компромиссное недоминируемое решение равновесное по Нэшу.
Выбор векторного Нэш-решения относительно идеальной (утопической) для множества допустимых решений точки (СТЭК-3).
Коалиционное равновесие при фиксированном разбиении МK = P ММС вырождается в векторное равновесие. Поиск векторного равновесия (векторного Нэш-равновесия и W-равновесия), является достаточно сложной задачей с собственным программным обеспечением.
Каждая коалиция теперь имеет векторный показатель, что учитывает элемент субъективности взаимной информации о приоритетности показателей партнёров. Естественно, что скаляризация показателей коалиции с заданными весами приводит к частному случаю векторного Нэш-равновесия: скалярному равновесию по Нэшу.
Поэтому при исследовании векторного равновесия по сравнению со скалярным, во-первых, возрастает размерность множества показателей, во-вторых, возрастает число равновесных решений, так как даже при единственности скалярного равновесия перебор вектора весов приводит к множеству решений. Увеличение размерности задачи и расширение множества равновесных решений на множестве допустимых решений приводит к необходимости искать компромиссное решение среди недоминируемых векторных равновесий (![]() ), наиболее близкое к идеальной точке над множеством допустимых решений по критерию:
), наиболее близкое к идеальной точке над множеством допустимых решений по критерию:
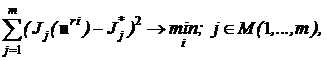 (2.4)
(2.4)
где
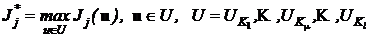 , (2.5)
, (2.5)
где UKm – множество параметризованных управлений (решений) коалиции Km, m = 1,...,l. Полученное на основе (2.4), (2.5) решение является наилучшим векторно-равновесным решением для всех коалиций, а поэтому является компромиссным в условиях необязательных соглашений.
Общий метод определения компромисса принимает вид следующей многоэтапной последовательности.
Этап 1. Получение векторных Нэш-равновесий.
Этап 2. Получение множества недоминируемых векторных равновесий.
Этап 3. Получение идеального решения на основе критерия (2.5).
Этап 4. Получение компромиссного решения на конечном множестве недоминируемых векторных равновесий на основе критерия (2.4).
Ввиду сложности решения данной задачи, особенно на первом этапе, данный алгоритм реализован в универсальной программной среде «MATLAB». Надлежащая параметризация программно-корректируемого закона управления и использование параллельной вычислительной среды позволяет реализовать алгоритм в реальном времени.
Формирование Парето–Нэш-области компромиссов (ПНОК) (СТЭК-4).
Предыдущие СТЭК-1 – СТЭК-3 позволяли получить лучшие решения в рамках одного и того же множества стабильных решений. Данная ПНОК позволяет выделить на области допустимых решений или на области допустимых значений показателей подобласть, где наиболее вероятны следующие шаги по формированию стратегических и нестратегических компромиссов на основе соответственно необязательных соглашений с определённой устойчивостью к отклонениям и строго договорных процедур с обязательными соглашениями и процедурами наказания при невыполнении соглашений, а также определённой «смеси» необязательных и обязательных соглашений. Поэтому, с одной стороны, данная ПНОК является базой для формирования новых компромиссов, с другой стороны, при определенной близости компромиссного значения показателей на основе предыдущих СТЭК к Парето-границе области показателей выделяется малая ОК, каждая точка которой с определённой степенью грубости играет роль собственно СТЭК-4, а в пределе превращается в ПСТЭК.
Всё это следует из определения ПНОК на области допустимых значений показателей – свёрток в смысле СТЭК-1 и СТЭК-2 или полного вектора в смысле СТЭК-3.
Определение 2.2. ПНОК удовлетворяет системе неравенств:
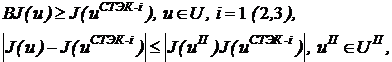 (2.6)
(2.6)
где первое неравенство системы (2.6) имеет смысл многогранного конуса доминирования с матрицей В = Е и вершиной в точке J(uСТЭК-i), а второе имеет смысл семейства лучей, соединяющих точку СТЭК и соответствующее лучу решение ![]() из подмножества UП Парето-оптимальных решений, также удовлетворяющих первому неравенству. Рисунок 2.1 иллюстрирует данное определение для двухобъектной ММС со скалярными показателями объектов.
из подмножества UП Парето-оптимальных решений, также удовлетворяющих первому неравенству. Рисунок 2.1 иллюстрирует данное определение для двухобъектной ММС со скалярными показателями объектов.
Метод получения ПНОК базируется на комбинации алгоритмов Парето-оптимизации, Нэш-оптимизации и получения СТЭК-1 (2,3), что может быть представлено в упрощённом виде следующей процедурой.
Этап 1. Получение множества скалярных (векторных) недоминируемых Нэш-равновесий.
Этап 2. Определение стабильно-эффективных решений СТЭК-1 (2,3).
Этап 3. Формирование конуса доминирования (2.6) на области значений показателей, как на отображении области решений.
Этап 4. Получение области Парето-оптимальных решений и подобласти U П на основе конуса (2.6).
Этап 5. Формирование системы значений показателей и системы решений, удовлетворяющих ПНОК, с элементами проективно-графического анализа.
Для реализации данного алгоритма с использованием СТЭК-1, СТЭК-2 формируются интерактивные процедуры на основе модулей Парето–Нэш-оптимизации в программной среде ПС «MOMДИС» с использованием графических экранных отображений. Данный алгоритм с использованием СТЭК-3 реализован в среде «MATLAB».
Взаимосвязь ПНОК и области УКУ-решений (СТЭК-5).
Векторное и скалярное равновесие при фиксированной коалиционной структуре являются частными случаями коалиционного равновесия, так как каждая коалиция стремится обеспечить свою локальную Парето-оптимальность в рамках всей локальной области, ее подобласти или точки соответственно, а равновесное решение по определению является V-решением (не содержит эффективных угроз, против которых нет контругроз).
УКУ-равновесие по Вайсборду–Жуковскому является модификацией V-решения и принадлежит к множеству коалиционных равновесий, если допустимое множество коалиционных структур позволяет сформировать контругрозу.
Если точка УКУ-равновесия единственная и попадает на ПНОК, то в сравнении с Нэш-равновесной точкой она более выгодная для ММС (рис. 2.2) и является устойчивым компромиссным решением с предостережением к отклонению в условиях необязательных соглашений.
В более общем случае может иметь место подмножество УКУ-равновесий, для которого по определению Нэш-вершина ПНОК является граничной точкой (из-за обращения неравенства угрозы). Тогда вступают в действие три ранее рассмотренные вида СТЭК в применении к множеству УКУ или формируется алгоритм выбора точки УКУ, наиболее близкой к Парето-границе и, например, учитывающий уравновешивание потерь (рис. 2.3).
Из анализа прикладных результатов выявляются некоторые общие закономерности, которые сложно получить «прямыми» теоретическими исследованиями, – это неединственность УКУ-решений и попадание большей части решений на ПНОК.
Если ресурсы коалиций не равны, то ПНОК содержит подмножество точек УКУ, которые смещены в пользу коалиции с большими ресурсами. При выравнивании ресурсов число УКУ-решений увеличивается, а множество УКУ существенно пересекается с ПНОК (применяя в некоторых случаях очертания ПНОК), причём часть точек УКУ попадает на Парето-границу ПНОК.
Следовательно, может быть сформулировано следующее утверждение общего характера.
Утверждение 2.1. ПНОК содержит подмножество УКУ-оптимальных решений, а при выравнивании ресурсов коалиций – объектов в ММС число решений возрастает и их множество существенно пересекается с ПНОК, причём Парето-граница ПНОК содержит УКУ-решения.
Замечание 2.1. Из последней части утверждения следует, что точки Парето-границы ПНОК могут выбираться как начальные приближения компромиссных УКУ-решений.
Взаимосвязь ПНОК и множества дележей (СТЭК-6).
Метод получения дележей по Шепли детально обсуждается в главе 5. В условиях необязательных соглашений делёж по Шепли обосновывает выбор такого коалиционного равновесия, которое является наиболее подходящим для возможного объединения в кооперацию при переходе к строго договорным компромиссам с обязательным выполнением соглашения.
Поэтому полезно исследовать взаимосвязь ПНОК и множества дележей.
Утверждение 2.2. Парето-граница ПНОК для однотипных ММС удовлетворяет свойствам коллективной и индивидуальной рациональности дележей.
В общем случае ПНОК принадлежит прямоугольному многогранному конусу с вершиной в ![]() (i = 1,…,N), который ограничен Парето-границей
(i = 1,…,N), который ограничен Парето-границей ![]() (i = 1,…,N), и следовательно,
(i = 1,…,N), и следовательно,
![]() ³ Ji³
³ Ji³ ![]() , (i = 1,…,N).
, (i = 1,…,N).
Тогда характеристическая функция, характеризующая индивидуальную эффективность, имеет вид
v (i) = ![]() из (
из (![]() ,
, ![]() ).
).
При этом
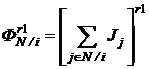 .
.
Также известно, что
![]() ³
³ ![]() ³
³ ![]() = v(i), i = (1,…,N),
= v(i), i = (1,…,N),
что является условием индивидуальной рациональности дележа на Парето-точках ПНОК. Условие коллективной рациональности Парето-точки ПНОК выполняется тождественно, так как по определению дележа
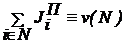 .
.
Таким образом, Парето-граница ПНОК обладает свойством коллективной и индивидуальной рациональности.
Собственно, СТЭК-6 имеет смысл либо ПСТЭК, либо УКУ-равновесия, которые оказались на Парето-границе ПНОК в окрестности найденной точки дележа по Шепли.
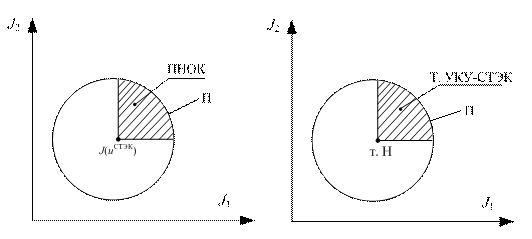
Рис. 2.1. Парето–Нэш-область компромиссов для двухобъектной ММС | Рис. 2.2. Частный случай СТЭК-5: |
Выбор наиболее эффективного УКУ-решения на основе ПНОК и точки дележа Шепли
(СТЭК-7).
Рассмотренный СТЭК-6 является частным случаем более общего СТЭК, когда множество УКУ-равновесий имеет общий характер положения в ПНОК, например так, как показано для N = 2 на рис. 2.3.
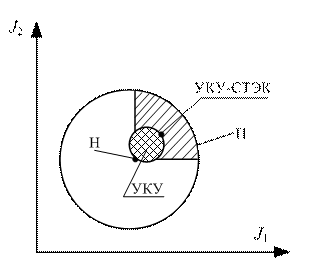
Рис.2.3. Общий характер положения УКУ-равновесия на ПНОК
Тогда СТЭК-5 и СТЭК-6 обобщаются в виде СТЭК-7, который имеет наиболее общий вид в условиях необязательных соглашений и содержит предыдущие СТЭК-1 – СТЭК-6 как частные случаи или компоненты.
Определение 2.3. Общий стабильно-эффективный компромисс в условиях необязательных соглашений формируется как устойчивое решение с предостережением, обладающее максимальной степенью близости к оценке наилучшего результата, который может быть достигнут при кооперативном объединении на основе обязательных соглашений. Таким свойством обладает УКУ-равновесие на ПНОК, которое является наиболее близким к точке дележа по Шепли или к ее максимальной реализуемой предпосылке.
Общая схема метода определения данного СТЭК заключается в последовательном поэтапном решении следующих задач.
Этап 1. Определение множества Нэш-равновесий.
Этап 2. Определение наилучшего Нэш-решения на основе СТЭК-1, СТЭК-2, СТЭК-3.
Этап 3. Определение множества УКУ-равновесных решений.
Этап 4. Формирование подмножества УКУ-решений, удовлетворяющих условиям (2.6) на основе СТЭК-4, СТЭК-5.
Этап 5. Определение предпосылки дележа по Шепли на ПНОК (СТЭК-6).
Этап 6. Определение УКУ-решения, принадлежащего ПНОК и наиболее близкого к точке дележа по Шепли.
Собственно, СТЭК-7 формируется на этапе 6 метода и заключается в решении задачи перебора следующего вида:
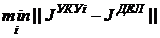 ,
,
где ![]() = J(uiУКУ) – значение вектора показателей i-го УКУ-решения uiУКУ на ПНОК;
= J(uiУКУ) – значение вектора показателей i-го УКУ-решения uiУКУ на ПНОК; ![]() – значение вектора показателей точки дележа по Шепли.
– значение вектора показателей точки дележа по Шепли.
Элементы приближений при формировании управляющих функций, базовые модули и интерактивные процедуры в рамках специализированной программной системы «МОМДИС» и универсальной ПС «MATLAB», а также параллельные алгоритмы реализации позволяют сформировать процесс автоматизированного проектирования управления конкретной ММС на основе СТЭК-комбинации Парето–Нэш–УКУ–Шепли-решений.
Расчетная часть
Исходные данные
Неизменяемые параметры для базового варианта имеют вид:
1. Общий момент инерции зеркала ![]() [
[![]() ]
]
2. Максимальная скорость слежения ![]() [угл. с./с]
[угл. с./с]
3. Максимальная ошибка наведения ![]() [угл. с]
[угл. с]
4. Максимальное ускорение слежения ![]() [угл. с./с2]
[угл. с./с2]
5. Показатель колебательности контура положения 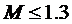
6. Показатель колебательности контура скорости 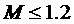
7. Постоянная времени фильтра ![]() [c]
[c]
8. Время реакции контура скорости ![]() [мc]
[мc]
Исследование эффективности конфликтного взаимодействия проводится в следующих направлениях.
- Изменение весовых параметров
Таблица 1
Базовый вариант | Вариант более значимых показателей |
|
|
- Влияние входящих управляющих воздействий в виде физической ступеньки:
1. 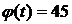 [град]=162000 [угл. с] (базовый вариант)
[град]=162000 [угл. с] (базовый вариант)
2. 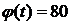 [град]=288000 [угл. с]
[град]=288000 [угл. с]
- Учет влияния коэффициента звена скоростной компенсации:
1. 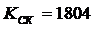 (базовый вариант)
(базовый вариант)
2. 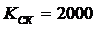
3. 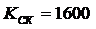
- Учет влияния значения полосы пропускания контура скорости:
1. 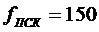 [Гц] (базовый вариант)
[Гц] (базовый вариант)
2. 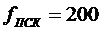 [Гц]
[Гц]
3. 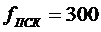 [Гц]
[Гц]
Результаты моделирования базового варианта.
Область показателей, точка Шепли, область УКУ и Парето решений, точки СТЭК-1 и СТЭК-7.
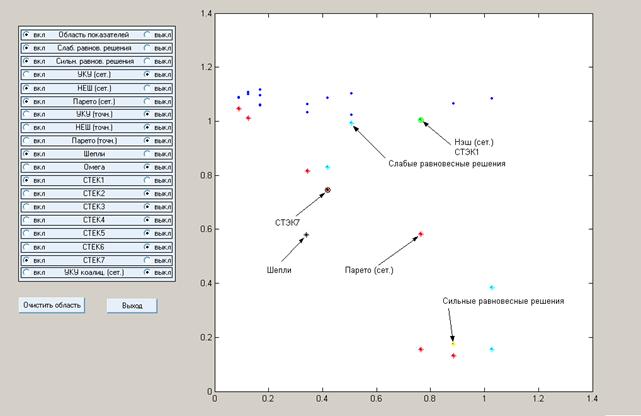
Результаты оптимизации:
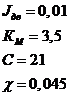
Результаты вариаций:
1) ![]() [град]=162000 [угл. с],
[град]=162000 [угл. с], 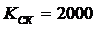 ,
, ![]() [Гц]
[Гц]
Область показателей, точка Шепли, область УКУ и Парето решений, точки СТЭК-1 и СТЭК-7.
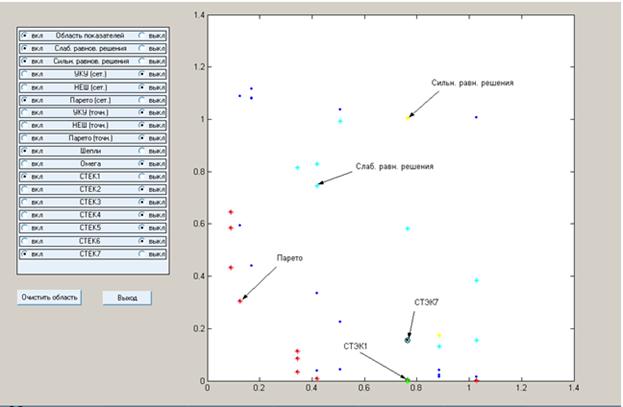
Результаты оптимизации:
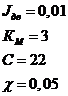
2) ![]() [град]=162000 [угл. с],
[град]=162000 [угл. с], 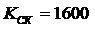 ,
, ![]() [Гц]
[Гц]
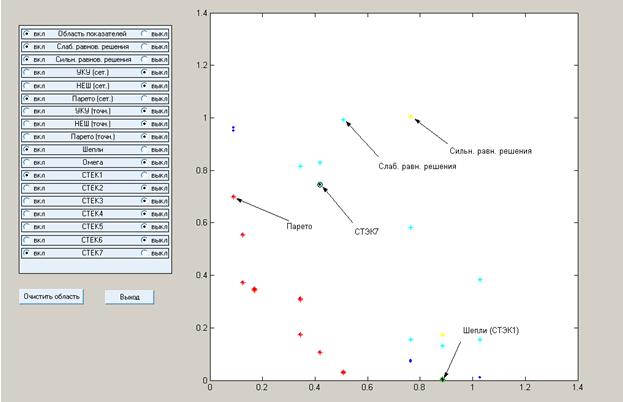
Результаты оптимизации: