Оценка доходности и риска рыночного актива при инвестировании

Тема 1. Оценка доходности и риска рыночного актива при инвестировании.

Всем нам приходится получать и расходовать деньги. Но очень редко количество поступающих денег в точности равно тому количеству, которое хотелось бы в данный момент потратить. Если образовался избыток денег, его можно положить в тумбочку или закопать на даче — сделать сбережения. Когда возникнет необходимость траты, эти деньги можно будет достать, их количество не изменится. Сбережения — это выбор потратить деньги в будущий момент времени взамен того, чтобы потратить их сейчас.

Но есть и другая возможность — дать сберегаемые деньги взаймы или купить на них что-нибудь, чтобы в будущем получить денег больше, чем потрачено в настоящем. Такой процесс (все то, что делается со сбережениями, чтобы они росли с течением времени) называется инвестированием, а тот, кто его осуществляет — инвестором.

Предположим, инвестор желает вместо 100 руб. сейчас получить через год 104 руб. Он может дать эти деньги взаймы или положить в банк под 4% (реальный процент), но лишь в предположении, что покупательная сила денег не изменится (нулевая инфляция). Если же инфляция ожидается ненулевой (например, 10%), то инвестор потребует более высокий процент, чтобы через год на полученные деньги можно было бы купить столько же товаров, сколько сейчас — на 104 руб., а именно 14,4% (номинальный процент). Номинальный процент рассчитывается по формуле Фишера:

Номинальный процент = (1 + реальный процент) * (1 + ожидаемая инфляция) - 1

Далее, если есть вероятность того, что заемщик не отдаст долг своевременно (или банк обанкротится), инвестор потребует еще более высокий процент в качестве платы за риск. К примеру, если при тех же условиях банк принимает депозит под 20%, это означает, что он предлагает премию за риск в 6,6% (6,6% = 20% - 14,4%).

Таким образом, инвестиции — это откладывание нынешнего потребления известного количества денег на некоторый период времени, с целью получения в будущем ожидаемого количества денег, достаточного для компенсации: 1. времени, на которое откладывается потребление; 2. ожидаемой инфляции; 3. риска. Так как фиксированное количество денег сегодня меняется на ожидаемый поток платежей в будущем, риск при инвестициях возникает всегда — невозможно точно указать, что произойдет в будущем.

1.2 Доходность

У любых инвестиций есть два аспекта — доходность и риск. Расчет доходности простой. Допустим, два года назад было инвестировано 150 руб., а сегодня получено 300 руб. Чтобы подсчитать доходность за период инвестирования, нужно конечную стоимость разделить на начальную и вычесть единицу: 300 / 150 – 1 = 100%.

Чтобы подсчитать в этом же случае годовую доходность, нужно вновь конечную стоимость разделить на начальную, далее извлечь корень той степени, сколько лет длился период, и после этого вычесть единицу:

(300 / 150)1/2 – 1 = 41,4%

Еще один пример. Предположим, было инвестировано 100 руб., через три месяца получено 108 руб. В этом случае, очевидно, доходность за период будет 8%, а годовая:

(108 / 100)(1/(3/12))– 1 = 36,0%

При вычислении годовой доходности неявно предполагается, что такая же доходность будет и все остальное время года. Период инвестиций составил три месяца из двенадцати в одном году — отсюда показатель степени. Если период инвестиций измеряется в днях, то делить их количество нужно на 365.

Историческая доходность вложений в какой-нибудь актив определяется двумя способами. Самый простой – подсчитать среднеарифметическую доходность: просуммировать доходность каждого года за ряд лет и разделить на количество лет. В качестве альтернативы можно подсчитать среднегеометрическую доходность: перемножить отношения конечной суммы инвестиций к начальной за ряд лет и извлечь из произведения корень степени, равной количеству лет (отношение конечной суммы инвестиций к начальной равно единице плюс доходность). Проиллюстрируем эти способы на простом примере:

Доходность за три года:

Среднеарифметическая: (20,0% + 20,0% - 16,7%) / 3 = 7,8%

Среднегеометрическая: (1,20 * 1,20 * 0,83)1/3 = 6,3%

Легко видеть, что среднегеометрическая доходность в точности равна годовой доходности, при определении которой используются только начальная и конечная сумма инвестиций:

(120 / 100)1/3 = 6,3%

Среднегеометрическая доходность никогда не превышает среднеарифметической, и равна ей только в том случае, когда доходности за каждый год строго равны между собой — это доказывается математически.

Иными словами, среднеарифметическую доходность можно использовать только тогда, когда по окончанию расчетного периода прибыль изымается со счета (восполняется убыток) и новый период начинается точно с той же суммы, что и начальный период. Если же производится полное реинвестирование суммы прибыли (или не восполняется убыток), то пользоваться надо среднегеометрической доходностью, которая позволяет учитывать сложные проценты. Первая ситуация носит несколько искусственный характер, вторая более приближена к жизни, поэтому при подсчете исторической доходности за ряд лет обычно используют геометрическое усреднение, что указывается в стандартах и подразумевается по умолчанию.

Некритическое использование среднеарифметической доходности приводит к парадоксу. Предположим, инвестиции в первый год выросли на 100%, а во второй упали на 50%. Конечная сумма равна начальной, и среднегеометрическая доходность, как и положено, будет нулевой. Среднеарифметическая же будет +25%.

Многие инвесторы, если спросить их, в какую сторону изменилась цена, если вчера она упала на 5%, а сегодня выросла на 5%, ответят, что цена не изменилась — очень уж хочется пользоваться таким простым арифметическим усреднением. На самом деле цена, конечно, снизилась (помните — среднегеометрическая доходность никогда не превышает среднеарифметическую?). Для ориентации полезна следующая таблица (если цена снизилась на Х%, она должна возрасти на Y%, чтобы вернуться к первоначальному уровню):

Среднегеометрическая доходность за много лет обычно используется для прогнозирования будущей среднегодовой доходности при долгосрочных вложениях в тот же актив. Среднеарифметическая доходность используется для прогнозирования будущей доходности в течение следующего года. Выглядит странно; тем не менее, так оно и есть, если вспомнить теорию статистики. Но в результате прогноз роста рынка акций на будущий год может постоянно завышаться.

Доходность портфеля активов рассчитывается как средневзвешенная доходностей отдельных активов, входящих в портфель, с весами, соответствующими начальным долям активов в портфеле (сумма весов всегда равна единице). Например, если был составлен портфель, состоящий из 40% РАО ЕЭС и 60% Лукойла, то при доходности РАО ЕЭС 50% а Лукойла — 30%, доходность портфеля составила 0,4*0,5 + 0,6*0,3 = 0,38 или 38%.

Риск является мерой неуверенности в том, что инвестиции принесут в точности ожидаемый результат.

Для оценки риска инвестиционного портфеля применяются показатели, которые показывают, насколько будет варьироваться ожидаемый доход или доходность ценных бумаг, входящих в портфель. В экономических расчетах наиболее часто используются следующие показатели вариабельности доходности:

·  размах вариации (R);

·  вариация (var);

·  среднее квадратическое отклонение признака(σ);

·  коэффициент вариации (CV);

·  ковариация (cov);

·  корреляция (corr).

Если доходность инвестиций в некий актив в будущем году ожидается, к примеру, 10%, то такая оценка называется точечной. Если рассмотреть разные варианты (сценарии) возможных изменений на рынке, то, скорее всего, окажется, что возможная доходность меняется, например, от –5% до +25%. Можно определить ожидаемую среднюю доходность, арифметически усреднив возможные доходности с весами, равными вероятностям получения этих доходностей (оценки как возможных доходностей, так и вероятностей, субъективны). Итак,

Ожидаемая, или средняя, доходность = Сумма (возможная доходность * вероятность возможной доходности)

Проиллюстрируем примерами.

Пример 1. Если возможна одна-единственная доходность, то ее вероятность в точности равна 1, и ожидаемая доходность R1 равна единственно возможной (скажем, 19%). Такое бывает при инвестициях в краткосрочные облигации, когда дело доводится до погашения бумаги по номиналу.

Пример 2. Теперь допустим, что речь идет об акции определенного эмитента. И в первом приближении просчитываются три сценария развития событий: 1. Рост экономики ускоряется по отношению к предыдущему году (вероятность 20%), акция вырастет на 30%; 2. Рост экономики остается на прежнем уровне (вероятность 70%), акция вырастет на 20%; 3. Рост экономики замедлится (вероятность 10%), акция упадет на 10%. Тогда ожидаемая доходность:

 R2 = (0,20 * 0,30) + (0,70 * 0,20) + (0,10 * (-0,10)) = 0,19 или 19%.

Пример 3. Здесь речь пойдет об акциях компании, появившейся на рынке с новым продуктом. Снова три сценария: 1. Продукт пользуется повышенным спросом (вероятность 30%), доходность 100%; 2. продукт пользуется умеренным спросом (вероятность 40%), доходность 40%; 3. Продукт не пользуется спросом (вероятность 30%), доходность –90%. Ожидаемая доходность:

 R3 = (0,30 * 1,00) + (0,40 * 0,40) + (0,30 * (-0,90)) = 0,19 или 19%.

Ожидаемые доходности во всех трех примерах в точности равны. Но какой окажется доходность в действительности, в последних двух примерах точно сказать уже нельзя. Следовательно, эти инвестиции будут рискованными. Но легко видеть, что риск у них разный.

При расчете на рынке капитала гораздо более ценен перспективный анализ, и здесь большинство величин, представляющих интерес, оцениваются в вероятностных терминах. И здесь основная проблема - правильно оценить ожидаемые значения исходных параметров. Для выполнения этой задачи созданы специальные экспертные группы. Они занимаются анализом биржевого рынка, обработкой и систематизацией полученных данных и составлением прогнозов – экспертных оценок по ценным бумагам. Экспертные оценки для ценных бумаг наиболее известных компаний, работающих на российском и зарубежном рынках, периодически публикуются в российской газете «Финансовые известия».

Для оценки ожидаемой доходности актива, экспертами делается три оценки:

·  пессимистическая (kp);

·  наиболее вероятная (kml);

·  оптимистическая (ko).

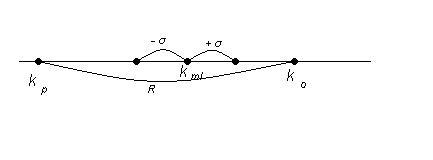
Для наиболее общей оценки риска на основании показателей пессимистической и оптимистической оценок, рассчитывается размах вариации (R):

R= ko - kp (1);

Считается, что чем выше значение полученного показателя, тем выше риск по данному активу, поскольку этот показатель показывает уровень размаха доходности ценной бумаги.

Пример 1: Предпринимателю необходимо выбрать лучший из двух альтернативных финансовых активов:

Если оценивать актив исходя из размаха вариации, то лучшим является вариант А.

Однако, размах вариации имеет существенный недостаток - большую зависимость показателя от крайних значений ранжированного ряда. Следует отметить, что при расчете размаха вариации, не учитывается вероятность наступления этих крайних значений. Иногда она может быть крайне мала. Поэтому для получения объективной оценки эффективности инвестирования данного показателя недостаточно. Он может служить только для целей довольно грубого, поверхностного анализа, или в качестве вспомогательного критерия.

Показатель «наиболее вероятная доходность» - является более точным и объективным, поскольку при его расчете учитывается вероятность получения той или иной ожидаемой доходности. Расчет показателя наиболее вероятной доходности производится по формуле:

, где

ki –i-тая доходность;

pi-вероятность получения i-той доходности.

Пример 2: По оценкам экспертов имеются следующие данные об активах А и В:

Рассчитать наиболее вероятную доходность актива А и актива В.

Решение:

Наиболее вероятная доходность актива А - kml (A) = 14%*0,1+16%*0,6+18%*0,3=16,4%

Наиболее вероятная доходность актива В - kml (В) = 13%*0,1+17%*0,6+21%*0,3=17,8%

Таким образом, если оценивать предложенные проекты исходя из вариабельности, то более привлекательным является актив А. Однако, исходя из наиболее вероятной доходности, более привлекателен проект В, поскольку имеет большую вероятную доходность.

Инвестор всегда делает свой выбор в зависимости от склонности или несклонности к риску, и от цели инвестиций. Инвестор, более склонный к риску, выберет более рискованный, но и более доходный проект В, тогда как консервативно настроенный инвестор предпочтет актив А.

Еще одним, наиболее часто используемым показателем при анализе инвестиционных проектов и выборе активов является показатель среднеквадратического отклонения доходности (σ).

Показатель среднеквадратического отклонения доходности (σ) показывает, на сколько процентов в среднем будет отклоняться наиболее вероятная доходность i-го актива.

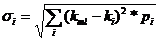
Графически показатели, служащие для оценки риска инвесттиций R, ko, kp, kml, σi, можно представить - следующим образом:

CV – коэффициент вариации показывает, какой процент от ожидаемой доходности составляет среднеквадратическое отклонение (σi) доходности актива, то есть какой процент ожидаемой доходности находится «в зоне риска».